屋顶H型垂直轴风力机气动性能CFD计算方法研究
■ 梅毅 曲建俊
(1.中国电力工程顾问集团华北电力设计院有限公司;2.哈尔滨工业大学机电工程学院)
0 引言
风能是一种清洁的可再生能源,风力发电提供的大量清洁电力可替代常规火力发电,具有巨大的生态环境效益和社会效益。我国风电产业自2006年以来保持强劲的发展势头,装机容量屡创新高。然而,在风电装机高速增长的同时,弃风限电问题也日益严重[1]。《风电发展“十三五”规划》中明确指出,在负荷中心发展分布式风力发电,是解决风电消纳问题的重要途径之一。容量相对较小、分散布置的分布式风电,已成为电力系统的重要组成部分[2,3]。近年来,城市楼顶风能的利用引起了国内外学者的广泛关注[4-6]。与应用在野外风场的水平轴余量不同,垂直轴风力机具有无需对风装置、结构相对简单、安装维修方便等优势,尤其是H型垂直轴风力机,结构简单紧凑、占地面积小、噪音小,更适合作为城市屋顶的风能利用设备。因此,各国研究人员对其进行了针对性研究[7-9]。
风轮气动性能对风电机组的运行性能有重要影响。计算流体动力学(CFD)方法是研究垂直轴风力机气动性能的重要工具。Qin[10]和Untaroiu[11]比较了不同时间步长应用于H型垂直轴风力机CFD计算的结果,分别认为选用0.0002 s和0.001 s的时间步长合适,但研究结论缺乏通用性。Wang[12]和Edwards[13]分别用几种常用湍流模型计算了俯仰振荡翼型的升阻力系数,指出湍流模型SSTk-ω模型更适用于H型垂直轴风力机数值计算,但单个翼型俯仰振荡并不能反映旋转中的垂直轴风力机的工作状态。国家标准规定功率系数是反映风力机气动性能的重要参数之一[14],为保证H型垂直轴风力机气动性能数值计算结果可信,有必要考察CFD方法用于计算风轮功率系数的精度。本文以一种屋顶H型垂直轴风力机为研究对象,分析不同湍流模型、网格单元形状和时间步长对功率系数计算适用性的影响,以期为工程设计提供参考。
1 实验风力机
文献[15,16]所述的为一台用于城市屋顶风力发电的H型垂直轴风力机(如图1所示),在风洞中进行了全尺寸实验,与其他垂直轴风力机实验相比,该实验修正了由风轮支撑臂阻力及测试系统误差等因素造成的功率损失,获得了理想条件下的风力机功率系数值,实验功率系数值被各国学者用作H型垂直轴风力机数值模拟技术验证研究[17,18]。风力机风轮直径为2.5 m,旋转主轴直径为0.1 m,叶片为NACA0015翼型,当叶片长3 m,弦长0.4 m。当风速为10 m/s时,风洞实验测得尖速比λ=1.6时有最大功率系数0.34。该尖速比下,叶片的雷诺数在1×105~7.5×105之间变化,属于典型的垂直轴风力机工作的雷诺数范围[19]。本文采用不同湍流模型、网格单元形状和时间步长计算该实验风力机在各尖速比下的功率系数。鉴于现代垂直轴风力机常采用功率控制方法使之在最大功率系数下工作[20],本文还将通过比较风轮在最大功率系数时叶片的瞬时力矩来分析不同方法计算时差异产生的原因。

图1 实验风力机
2 评价指标
风力机流场是非定常流场,CFD计算获得相关气动性能数据前,须使流场充分发展。CFD方法是否适用要考虑计算效率和计算精度两个方面,即考察风轮旋转一周平均力矩达到收敛所需运算时间和风轮功率系数的计算精度。为使流场充分发展,规定风轮旋转一周平均力矩收敛的标准为相邻两周风轮平均力矩变化百分比r<1%,如式(1)所示:

式中,Tave(i)为风轮旋转第i周(i≥1)时的平均力矩。
设待考察的尖速比为n个,第j(j=1,2,...,n)个尖速比下功率系数CP的计算精度用εj来表示,如式(2)所示:
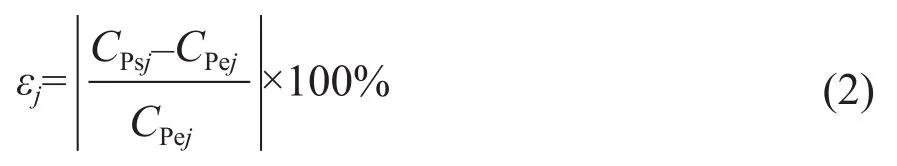
式中,CPej为第j个尖速比下风轮功率系数实验值;CPsj为第j个尖速比下风轮功率系数CFD计算值。CP可根据文献[21]中所述方法计算得到。
n个尖速比下CP的计算精度为εave,可根据式(3)计算:

3 数值计算方法
式(4)为由连续性方程和动量方程组成的控制方程组。

式中,ρ为空气密度,kg/m3;p为压强,Pa;μe为有效粘性系数;ui、uj分别为各坐标方向上的速度分量,m/s;t为时间,s。
由风轮二维模型组成的计算域ABCD如图2所示。设风轮直径为Φ,AD=BC=10Φ,AB=CD=20Φ,风轮回转中心距AD为5Φ,距BC为15Φ,风轮旋转域直径为2Φ。
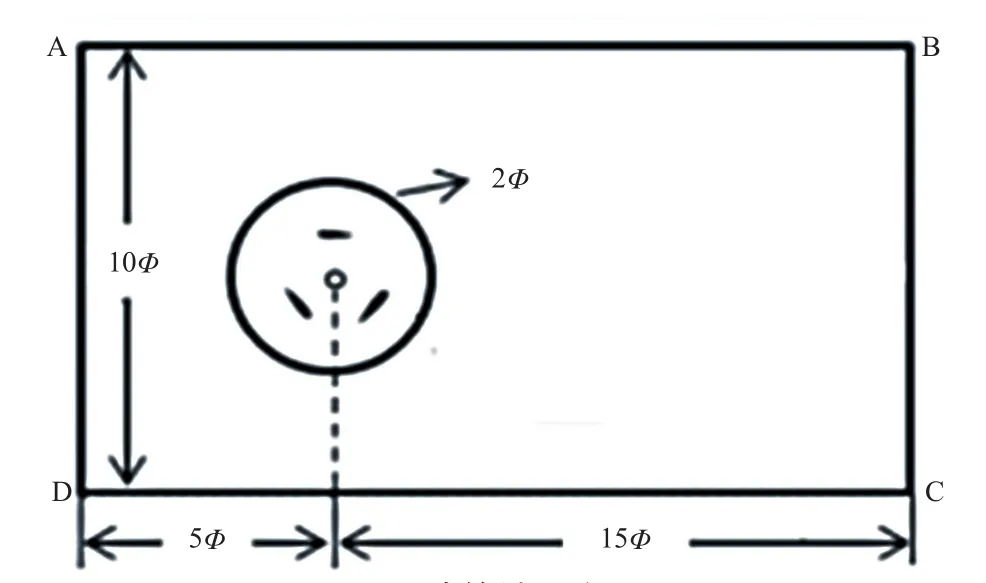
图2 计算域示意图
用Fluent求解控制方程组, AD为速度进口边界,来流速度为10 m/s,压力为大气压力,BC为压力出口边界。叶片、转轴及计算域边界AB和CD均为无滑移壁面,旋转域和外部静止域结合面为interface边界条件。用压力基求解方法,速度与压力耦合采用PISO算法,压力插值项为PRESTO格式,动量、湍动能和耗散率均采用QUICK格式,各项残差控制在10-5。
4 结果与分析
4.1 不同湍流模型比较
本文主要比较RNGk-ε模型、Realizablek-ε模型和SSTk-ω模型3种常用的两方程模型。计算域网格划分采用四边形单元,设置时间步长为风轮旋转0.5°所需时间。图3为尖速比λ=1.6时3种湍流模型计算的风轮平均力矩变化百分比。由图3可知,3种模型计算的风轮流场均在旋转至第6周时达到充分发展(r≤1%)。
表1为3种湍流模型在不同尖速比下的平均计算时间。由表1可知,RNGk-ε模型和Realizablek-ε模型计算的流场达到充分发展的平均耗时分别为8.46 h和8.28 h,而SSTk-ω模型为8.94 h。SSTk-ω模型计算耗时分别比RNGk-ε和Realizablek-ε模型多5.67%和7.97%。
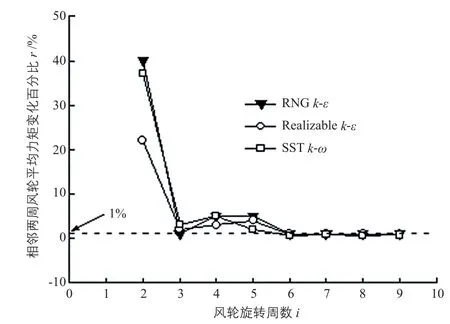
图3 λ=1.6时3种湍流模型计算的风轮平均力矩变化百分比

表1 3种湍流模型在不同尖速比下的平均计算时间
图4为3种湍流模型计算得到的风轮功率系数曲线,各尖速比下3种湍流模型的计算精度如表2所示。由表2可知,SSTk-ω模型的模拟精度最高。

图4 3种湍流模型计算的风轮功率系数曲线

表2 3种湍流模型的计算精度
图5为尖速比λ=1.6时,3种湍流模型计算的叶片瞬时力矩曲线图。从图5中可以看到,叶片瞬时力矩Tbinst在风轮上游区域达到峰值后逐渐降低,进入下游区域后维持在较低水平,原因是风轮吸收的大部分空气能量主要来自于风轮上游,下游叶片获取空气来流的能量较少。图5中3条瞬时力矩曲线相差较大处在60°<θ<150°区间内,SSTk-ω模型在吸收空气能量较大的上游区域模拟值大于RNGk-ε模型和Realizablek-ε模型,导致其功率系数计算结果高于后两者。
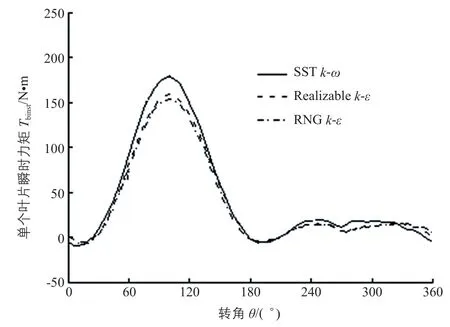
图5 3种湍流模型计算的叶片瞬时力矩曲线
4.2 不同网格单元形状比较
如图6所示,采用两种网格单元划分计算域,叶片周围用O型网格加密,叶片壁面网格数均为984,网格增长率均为1.07。用SSTk-ω模型封闭控制方程,设置非定常计算时间步长为风轮旋转0.5°所需时间。通过网格无关性检验确定计算域网格单元数量如表3所示。

图6 四边形和三角形网格划分计算域

表3 计算域网格数量对比
图7为尖速比λ=1.6时两种形状网格计算的风轮平均力矩变化百分比。由图7可知,采用四边形网格计算时,风轮旋转至第6周流场达到充分发展;而用三角形网格计算时,风轮旋转至第11周才满足收敛标准。

图7 λ=1.6时两种形状网格计算的风轮平均力矩变化百分比
表4为两种形状网格在不同尖速比下的平均计算时间。表4中数据表明,三角形网格模拟风轮旋转一周平均需0.87 h,耗时仅为四边形网格的58%;但四边形网格计算的收敛速度比三角形网格快5周,总耗时约为三角形网格的93%,计算效率相对更高。

表4 两种形状网格在不同尖速比下的平均计算时间
两种形状网格模拟所得风轮功率曲线如图8所示。
表5为两种形状网格的计算精度。从表5中可以看到,四边形网格的计算精度为7.40%,而三角形网格为7.89%,两者较为接近。
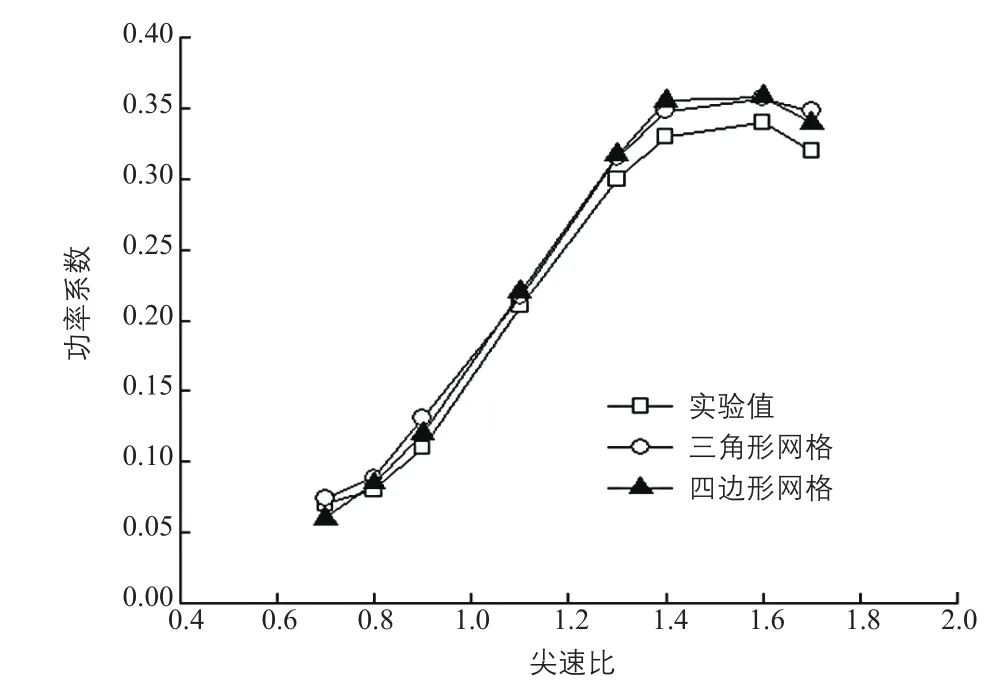
图8 两种形状网格计算的风轮功率系数曲线
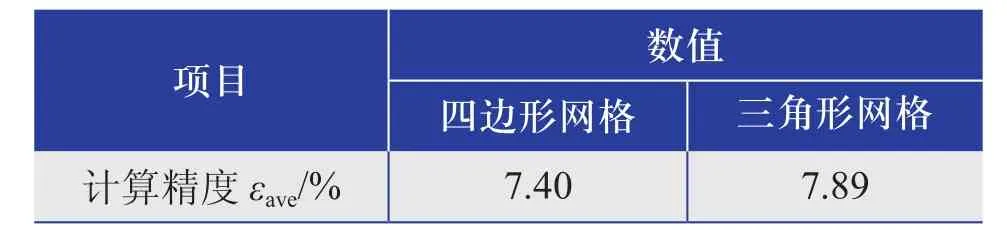
表5 两种形状网格的计算精度
图9为尖速比λ=1.6时,两种形状网格最大功率系数点时计算所得的叶片瞬时力矩曲线,其中相差较大之处主要位于80°<θ<120°区间内,而在其他位置两条曲线相对吻合。在网格尺寸和数量相同的条件下,四边形网格的节点数多于三角形网格,因此其模拟风轮旋转一周所需时间比三角形网格长。有限体积法将物理量存储于网格单元中心点上,沿网格边界线计算流场参数。垂直轴风力机风轮旋转时,流场会沿叶片壁面弯曲。四边形网格单元由于有4条边界线,在某些位置流体流动的矢量方向会沿着其中两条网格边界线;而三角形网格只有3条边界线,流体流动的矢量方向最多与其中一条网格边界线一致,因而采用四边形网格计算时产生的离散误差小于三角形网格,求解稳定性优于三角形网格,计算时流场达到稳定耗时更少。

图9 两种形状网格计算的叶片瞬时力矩曲线
4.3 不同时间步长比较
选取时间步长为风轮旋转 0.25°、0.5°、1°和2°所需时间用于CFD计算,记为0.25°ω-1、0.5°ω-1、1°ω-1和 2°ω-1。选用 SSTk-ω模型,计算域用四边形网格划分。图10为尖速比λ=1.6时4种时间步长计算的风轮平均力矩变化百分比,表6为4种时间步长在不同尖速比下的平均计算时间。
从图10和表6可以看出,较大的时间步长有利于提高Tave的收敛速度,减小时间步长导致计算时间增加,时间步长由2°ω-1缩短为1°ω-1、0.5°ω-1和 0.25°ω-1后,Tave平均收敛时间分别增至原收敛时间的1.55倍、2.98倍和4.66倍。
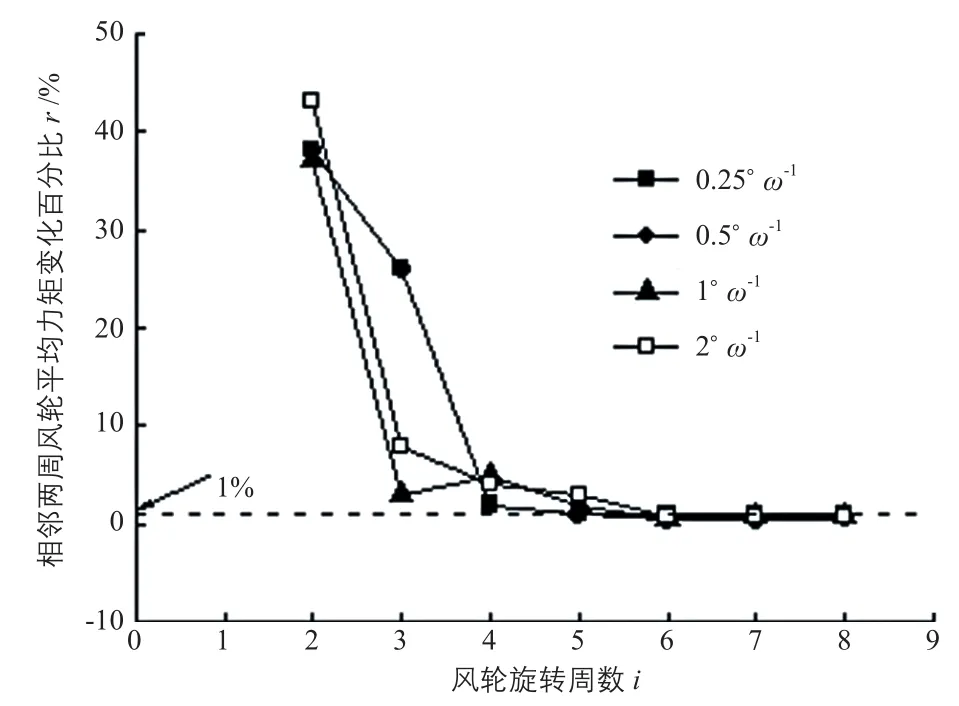
图10 λ=1.6时4种时间步长计算的风轮平均力矩变化百分比

表6 4种时间步长在不同尖速比下的平均计算时间
由图11和表7可知,减小时间步长有助于得到较准确的计算结果,但时间步长减小到一定程度后计算精度不会再大幅提高,且会使计算耗时增加。

图11 4种时间步长计算的风轮功率系数曲线

表7 4种时间步长的计算精度
从图12中可以看出,尖速比λ=1.6时,4种时间步长计算的叶片瞬时力矩差异主要发生在吸收风能较多的风轮上游区域,时间步长为2°ω-1和1°ω-1时计算的叶片瞬时力矩大于0.25°ω-1和0.5°ω-1时的结果,导致时间步长为2°ω-1和1°ω-1时计算的功率系数更大。

图12 4种时间步长计算的叶片瞬时力矩曲线
5 结论
改变湍流模型、网格单元类型和时间步长对屋顶H型垂直轴风力机功率系数的计算有较大影响,与实验数据对比验证的结果表明:
1)与 RNGk-ε和 Realizablek-ε模型相比,SSTk-ω模型计算耗时略长,但功率系数计算更接近实验值;
2)四边形网格的功率系数的总体计算精度与三角形网格相近,但计算效率更高;
3)采用较大的时间步长会降低风轮功率系数的计算精度,较小的时间步长可提高模拟精度,但会增加计算时间,将风轮旋转0.5º所需时间作为非定常计算的时间步长比较合适。
[1]熊敏鹏,张严,袁家海,等.我国风电的经济性评价及政策建议[J].中国能源,2016,38(10):20-26.
[2]张旭,吕新良,宋晓林,等.小型分布式风力发电系统设计及控制技术[J].陕西电力,2012,(1):75-78.
[3]张敏吉,梁嘉,孙洋洲,等.分布式风电——电池储能系统可用性分析[J].电力建设,2016,37(11):29-34.
[4]袁行飞,余俊伟.屋顶安装型风力机塔架风振反应分析[J].浙江大学学报(工学版),2013,17(11):1911-1916.
[5]潘雷.建筑环境中的风能利用[D].济南:山东建筑大学,2006.
[6]杨蓉,彭兴黔.高层建筑屋顶风能利用的数值模拟[J].华侨大学学报(自然科学版),2012,33(1):69-73.
[7]Battisti L,Zanne L,Anna S D,et al.Aerodynamic measurements on a vertical axis wind turbine in a large scale wind tunnel[J].Journal of Energy Resources Technology,2011,133:0312011-0312019.
[8]李岩,田川公太郎.叶片附着物对直线翼垂直轴风力机性能影响的风洞试验[J].可再生能源,2008,26(5):21-23.
[9]Keiana M.A modi fi ed streamtube model for vertical axis wind turbines[J].Wind Engineering,2012,36(2):145-180.
[10]Qin N,Howell R,Durrani N,et al.Unsteady fl ow simulation and dynamic stall behaviour of vertical axis wind turbine blades[J].Wind Engineering,2011,35(4):511-527.
[11]Untaroju A,Wood H G,Allaire P E,et al.Investigation of self-starting capability of vertical axis wind turbines using a computational fl uid dynamics approach[J].Journal of Solar Energy Engineering,2011,133:0410101-0410108.
[12]Wang S Y,Ingham D B,Ma L,et al.Numerical investigations on dynamic stall of low Reynolds number fl ow around oscillating airfoils[J].Computers and Fluids,2010,39(9):1529-1541.
[13]Edwards J M,Danao A L,Howell R J.Novel experimental power curve determination and computational methods for the performance analysis of vertical axis wind turbines[J].Journal of Solar Energy Engineering,2012,134(3):0310081-03100811.
[14]GB/T 19068.3-2003,离网型风力机发电机组 第3部分:风洞实验方法[S].
[15]Kooiman S J,Tullis S.Response of a vertical axis wind turbine to time varying wind conditions found within the urban environment[J].Wind Engineering,2010,34(40):389-401.
[16]Fiedler A J,Tullis S.Blade offset and pitch effects on a high solidity vertical axis wind turbine[J].Wind Engineering,2009,33(3):237-246.
[17]Almohammadi K M,Ingham D B,Ma L,et al.Computational fl uid dynamics (CFD) mesh independency techniques for a straight blade vertical axis wind turbine[J].Energy,2013,58:483-493.
[18]Islam M,Amin M R,Ting D S K,et al.Performance Analysis of a Small Capacity Straight Balded VAWT with Prospective Airfoils[A].46th AIAA Aerospace Science Meeting and Exhibit[C].Reno,2008.
[19]Islam M,Ting D S K,Fartaj A.Desirable airfoil features for small capacity straight bladed VAWT[J].Wind Engineering,2007,31(3):165-196.
[20]茅靖峰,吴爱华,吴国庆,等.垂直轴永磁直驱风力发电系统全风速功率控制[J].可再生能源,2014,32 (9) :1339-1345.
[21]梅毅,曲建俊,许明伟.垂直轴风力机叶片动态失速数值模拟[J].农业机械学报,2014,45(3):184-190.

