基于卫星导航接收机的测向技术研究

左晨宇，齐建中，宋 鹏，吕晟葳

(北方工业大学 信息工程学院，北京 100144)

0 引言

随着技术的发展，涌现出大批量的飞行器，载体的测向技术备受关注[1]。对载体测向是求解载体坐标系相对于当地水平坐标系的方位角，即俯仰角、偏航角和横滚角[2-4]。应用卫星导航接收机对载体测向，采取在载体上安置2个及以上的天线用于接收卫星信号，经射频前端运算、基带数字信号运算、导航信息处理及姿态信息运算，求得天线间的相对位置，然后经过相应的坐标转换，得到载体的位置、速度和姿态等信息。

求解载体姿态角必需使用准确的基线向量。卫星信号受到载波调制与伪码扩频影响时，接收机能够接收到2个量：与载波调制有关的载波相位和与伪码扩频有关的伪距[5]。由于伪码码片的长度远远大于载波的波长，因此伪距观测量的精确度远远小于载波相位观测量的精确度。通过伪距求解得到的相对位置的精度不能满足载体测向所需的要求，所以需要通过载波相位求解得到精确的基线向量，因此载波相位多被作为观测量应用于卫星系统的差分定位。对载波相位做差构造双差观测方程，此方程的未知量包括双差整周模糊度和双差噪声误差[6]。选择LAMBDA算法，将求解得到的整周模糊度带入到双差观测方程中，即可求解出高精度的基线向量。如何求解双差整周模糊度是核心问题。

本文所研究的基于卫星导航的测向技术，可弥补传统测向方法所不能满足的测向数据精度上的要求，并且能快速、准确、有效地计算出载体位置、速度和姿态信息，在对载体定位的同时为载体提供精确的姿态信息。

1 算法分析

评估算法好坏原则是求解得到对的整周模糊度时间的快慢。基于载体测向，2个接收机天线相近且距离已知。经分析，选择LAMBDA算法求解整周模糊度。LAMBDA算法的基本思想是基于目标函数分解的搜索算法，在规定的区域内进行最小值的搜索[7]。在几何学上，搜索区间是一个超维椭球，在这个椭球中的整数点或边沿上的整数点均为候选值，将所有候选值带入到目标函数中，其中最小的一个候选值就是整周模糊度的整数最小二乘估计。根据矩阵分解理论确定搜索区间，然后通过高斯整数变换减小各模糊度之间的互相关性，缩小搜索区间，从而缩短搜索的时间[8]。

1.1 构造观测方程及求解过程分析

载波相位观测方程可表示为：

(1)

对于2个接收机b和r，对分别接收到的卫星信号的载波相位观测方程做差可得：

(2)

引入卫星j，同卫星i一样可得到如式(2)所述方程，对2个方程做差，得到双差载波相位观测方程：

(3)

同理，对于多颗卫星而言，可得到双差载波相位方程组：

(4)

为使方程式个数T(M-1)≥未知量个数3T+(M-1)，需要联合T个历元时刻的双差载波相位方程组，可得

(5)

式中，T为整数；[·]为进一取整。显而易见，只有在共同捕获的卫星数超过5，同时联合历元数超过2，才可以将准确的相对位置坐标从双差载波相位方程组中求解得出。

若能求解整周模糊度，式(4)方程组仅有3个未知参数，方程式个数大于未知参数的个数，因此，可以求解相对位置的坐标。因此，求解双差载波相位方程的关键是确立双差整周模糊度[9]。

1.2 整周模糊度求解流程

LAMBDA算法求解整周模糊度大致可分为3步：求解双差整周模糊的浮点解，及浮点解的协方差矩阵；通过Z变换对协方差矩阵进行降相关处理；在变换后的搜索空间内进行最优整数解的搜索[10]。

1.2.1 浮点解的解算

要满足加权最小二乘法的条件，必须要结合若干个历元的双差载波相位方程组[11]。因此引入历元变量t，式(3)可以改写为：

Φt=-λ-1lt·lbr,t+N+εt，

(6)

式中，

(7)

联合K个历元的方程组，可以得到方程式个数大于未知量个数的超定方程组，用O(M-1)×3表示(M-1)×3阶全零矩阵、E(M-1)表示M-1阶单位矩阵，

(8)

这个方程组可以实现加权最小二乘法的需求，为此忽略接收机的噪声误差，能够求解浮点解和其协方差矩阵分别是：

(9)

(10)

式中，

(11)

(12)

(13)

(14)

O(M-1)×(M-1)为M-1阶全零方阵；QΦk(k=1,2,…,K)为历元k的双差载波相位观测量Φk的协方差矩阵，式(10)可以进一步改写如下：

(15)

式中，

(16)

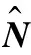
(17)

1.2.2 去相关处理

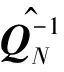
(18)

(19)

1.2.3 最优值搜索

构建合理的搜寻范围是搜寻整周模糊度整数解的第一步，即

(20)

χ2是搜索时的重中之重，因为它判定搜索范围的大小[14]。若χ2的选取值太大，范围中包括太多无谓的格点，导致搜寻时间更长；若χ2的选取值太小，导致最优解不在搜寻范围中，使得结果出现错误。综上只有选取恰当的χ2，既将搜索范围最小化，又含有至少一组整周模糊度的解。

(21)

采用序贯条件最小二乘估计法，在搜索空间内对整周模糊度整数解依次进行搜索，最终得到整周模糊度整数解的最优值[15]。Pi为搜索空间内的任意整数点，Pi的搜索范围为：

Pic-ri≤Pi≤Pic-ri，

(22)

式中，

(23)

(24)

由上述分析可知，从P0开始对双差整周模糊度进行搜索，计算得到P0的搜索空间及一组P0的候选整数解，采用其一候选整数解运算可知P1的搜寻范围，再采用同样方式搜寻P1。同理，遍历搜寻至第M个整周模糊度整数解。若整周模糊度Pi的搜索范围中未发现整数解，那么退回上一级元素Pi-1的搜索范围，将另一个候选整数代入式中继续搜索。求得一组M个整数组成的向量，这就是整周模糊度的最优解，再将整周模糊度的最优解Z反变换求得原始整周模糊度的最优整数解[16]。

1.2.4 整周模糊度的检验

得知整周模糊度以后，测量载波相位的解会产生误差，无法确保求得的整周模糊度完完全全准确，因此可检测整周模糊度整数解的准确度，包括基线长度的检验和模糊度值的检验，对错误的组合进行剔除[17]。

2 算法实现和数据分析

综上所述，证实LAMBDA算法适用于双差载波相位观测方程中整周模糊度求解[18]。为算法可行性分析检验，应用NovAtel公司的2台DL-V3型号接收机，构建单基线平台用于检验，将GPS L1频点看作信号源，在无遮挡开阔的楼顶利用串口捕获2台接收机的载波相位、共同卫星和共同时间等测姿需要的信息，之后利用Matlab对这些信息进行处理，从而求解姿态角，其详细过程如图1所示。

接收数据时，将主天线和辅天线东西方向放置，其中主天线位于西侧，两天线水平距离557.2 cm，垂直距离57.6 cm。偏航角、俯仰角结果分别如图2和图3所示。

图1 数据处理流程

图2 偏航角结果

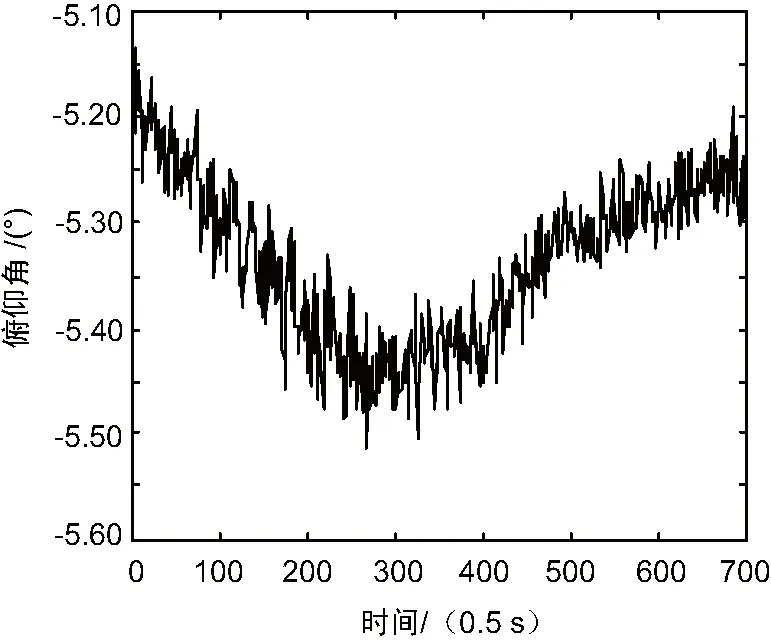
图3 俯仰角结果

由仿真结果可得偏航角的期望为179.349 6°而标准差为0.027 393°，俯仰角的期望为-5.335 2°而标准差为0.076 765°，和真实角度一致，而且稳定没有大的波动。通过测试结果可知，卫星导航测向接收机稳定工作后，测量误差基本在0.4°以内，满足对载体测向的需求。充分说明了本算法应用用于姿态测量的可行性。

3 结束语

本文主要对载体测向的关键技术进行研究分析。介绍载体测向所需的双差载波相位观测方程，研讨LAMBDA算法用于解算整周模糊度的可行性。着重介绍整周模糊度的求解过程，并分步骤进行叙述。再利用恰当的硬件载体实现算法。对算法进行仿真验证，上面的实验数据表明，在误差允许的范围内，此方法可以实现测量载体姿态角的功能。

[1] 刘宁，熊永良，王德军，等.一种新的GPS整周模糊度单历元求解算法[J].武汉大学学报(信息科学版)，2013，38(3)：291-294.

[2] 谢钢.GPS原理与接收机设计[M].北京：电子工业出版社，2011.

[3] 王晶.基于GPS的载体姿态测量及整周模糊度算法研究[D].哈尔滨：哈尔滨工程大学，2012.

[4] 马涛.光纤捷联惯导及其卫星深组合导航算法研究[D].哈尔滨：哈尔滨工程大学，2012.

[5] 鲁郁.GPS全球定位接收机——原理与软件实现[M].北京：电子工业出版社，2009.

[6] 彭天浪.基于多星座组合系统的载体姿态测量[D].南京：南京航空航天大学，2011.

[7] HATCH R,SHARPE R,YANG Y.An Innovative Algorithm for Carrier-Phase Navigation[R].Proceeding of ION GNSS,Long Beach,2004.

[8] 霍夫曼·韦伦霍夫，利希特内格尔，瓦斯勒.全球卫星导航系统GPS、GLONASS、Galileo及其系统[M].程鹏飞，蔡艳辉，文汉江，等，译.北京：测绘出版社，2009

[9] 赵蓓.RTK系统中整周模糊度求解技术研究[D].长沙：国防科学技术大学，2007.

[10] 周三奇.基于GPS的姿态测量系统研究[D].北京：北京交通大学，2009.

[11] 王珂.GPS测量算法与应用研究[D].重庆：重庆大学，2009.

[12] 赵蓓，王飞雪，孙广富，等.LAMBDA整周模糊度解算方法中的整数Z变换算法[J].导弹与制导学报，2008，28(3)：254-257.

[13] 夏娜，徐顺安，于春华，等.导航卫星载体测量进化算法研究[J].小型微型计算机系统，2010，31(5)：1006-1010.

[14] 朱学勇，齐志强.北斗测向技术[J].科学技术与工程，2009，9(17)：5085-5102.

[15] 刘玉梅，刘博峰.GPS双差观测量的方差—协方差分量估计[J].工程勘测，2007(7)：36-45.

[16] 谢世杰，涂国志.星基RTK系统[J].测绘通报，2004(10)：7-10.

[17] 钱进，吴金美，凌晓冬.线性回归模型加权最小二乘法估计的权值计算方法[J].理论新探，2007(9)：4-5.

[18] TEUNISSEN P.The Least-squares Ambiguity Decorrelation Adjustment:a Method for Fast GPS Integer Ambiguity Estimation[J].Journal of Geodesy,1995(70):65-82.