基于最大似然估计的16APSK载波捕获算法研究

冯晓文，李庆坤，任 彬

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.石家庄铁道大学 机械工程学院，河北 石家庄 050043)

0 引言

在卫星通信中，16APSK是一种极具潜力、利用载波幅度和相位同时承载信息的混合调制方式，在DVB-S2标准中已采用该调制方式[1]。16APSK的频谱利用率为4 bit/s/Hz，是BPSK体制的4倍。此外，相比于32APSK和64APSK，16APSK具有较低的复杂度，是一种折中的调制方式[2]。

接收机收到16APSK信号之后要在较短时间内完成载波同步，才可以进行有效的解调。载波捕获是完成载波同步的关键[3-4]。对于16APSK调制信号的载波捕获，一般有数据辅助和非数据辅助2种方法。数据辅助的方法是指采用低阶调制信号作为导频数据，辅助16APSK信号的捕获，但导频数据会占用一定的数据资源[5]。非数据辅助的方法是指直接对16APSK信号进行捕获，一般需要去除信号数据中的调制相位[6]，做FFT运算恢复载波，去除数据调制相位的过程一般是非线性运算，非线性运算会带来噪声的放大，因此在低信噪比条件下16APSK信号的捕获比较困难。

最大似然估计是一种未知参数估计的重要方法，可用于载波的频偏估计[7-10]，该方法无需对16APSK信号进行非线性运算，同时具有较高的估计精度。Kalman滤波是在最小均方误差估计基础上发展起来的一种递推估计算法[11]，可以最大限度地抑制信号中的噪声，降低噪声对频偏估计的影响。文献[12]提出了一种结合最大似然估计和Kalman滤波的方法，应用在BPSK的载波跟踪，在估计中采用平方变换去除调制信息。本文把结合最大似然估计和Kalman滤波的方法应用于16APSK的载波频偏捕获。该方法直接对包含载波频偏信息的16APSK信号相位序列进行最大似然频偏估计，并结合Kalman滤波，降低噪声对载波频偏估计的影响。

1 16APSK信号模型

16APSK的星座图由内外2个同心圆组成，研究较多的是4+12形式的16APSK[13]，即内圆有4个星座点，外圆有12个星座点。其星座点表达式为：

(1)

式中，r1和r2分别为内圆和外圆的半径，r2/r1=2.7；θ1和θ2分别为内圆和外圆上信号点的初始相位，这里θ1=π/4，θ2=π/12。

2 基于16APSK的最大似然估计算法

在无线通信中，最大似然估计常用于信号的载波频率估计。本文中，最大似然估计被应用于接收机中16APSK信号的载波频偏估计。假设接收机收到的16APSK信号为：

y(t)=a(t)cos(wit+θi)+b(t)sin(wit+θi)，

(2)

式中，a(t)和b(t)分别指同相正交分量的值，a(t)=real[Z(t)]，b(t)=imag[Z(t)]；wi和θi分别为接收信号的载波频率和相位。接收机的本振正交信号为：

(3)

式中，wo和θo分别为接收机本振的频率和相位。接收信号经过下变频处理，再通过低通滤波器滤除倍频分量，得到含有载波频偏的正交同相信号：

(4)

式中，Δw=wo-wi=2πΔf，Δθ=θo-θi+arctan[b(t)/a(t)]。Δf和Δθ是经过下变频低通滤波之后的残余频偏和相偏。由于Δθ可以通过锁相环捕获跟踪，因此本文只讨论Δf的估计。

可知，Δf是正弦函数的一个参数，如果已知正弦函数的采样样本，就可以通过最大似然估计对参数Δf进行估计。假设获得含有载波频偏的正交同相数字信号分别如下：

(5)

式中，k=0，1，...，K为采样样本的序列号；Ts为采样的周期；n(k)为均值为零、方差为σ2的离散高斯白噪声。在高信噪比条件下(信噪比大于10 dB)，式(5)中序列的离散相位信息在[-π，π]的一个2π周期内，其相位信息可以计算如下：

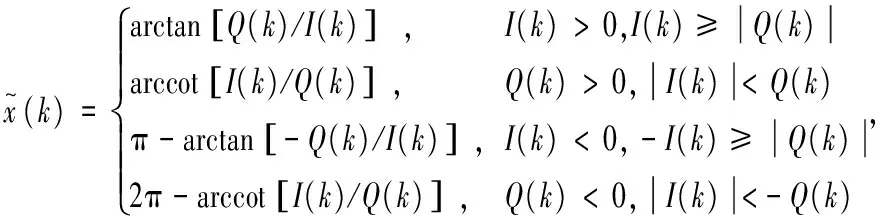
(6)

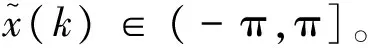
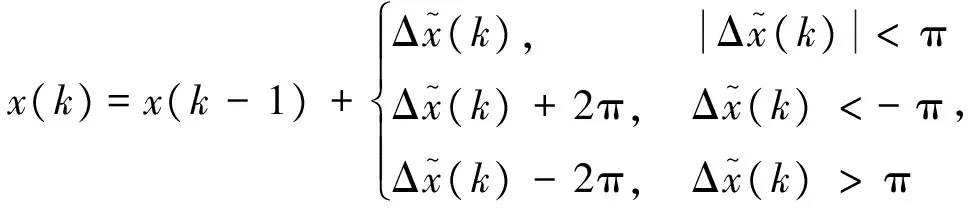
(7)

x(k)=2πkTsΔf+Δθ+v(k)，

(8)

式中，v(k)是由高斯白噪声引入的等效相位噪声[7]，其统计特性近似均值为零、方差为σ2的高斯分布。将式(8)写成向量的形式为：

X=Δfα+Δθβ+V，

(9)

式中，

X为服从高斯分布的随机矢量，其概率密度函数为：

(10)

式中，‖·‖2定义为‖X‖2=XTX。

使fx(X)的对数概率密度函数logfx(X)关于Δf和Δθ的梯度为零，即Δf，Δθlogfx(X)=0，可以获得关于Δf和Δθ的二元线性方程组，求得残余频差Δf的最大似然估计[7]为：

(11)

在上述算法中，最大似然估计使用的相位序列没有去除数据调制信息，这样避免了去除调制数据的非线性处理，但频偏估计使用的相位序列需要在一个调制数据符号内。通过该最大似然频偏估计算法，可以获得16APSK调制信号的载波频偏，该方法在高信噪比(信噪比大于10 dB)的情况，可以获得较准确的频偏估计[14]。在低信噪比的情况下，受噪声的干扰，频偏估计值偏差较大。因此，结合Kalman滤波抑制噪声是一种较好的解决方案。

3 结合Kalman滤波和最大似然估计的频偏估计算法

最大似然估计获得的频偏值受到噪声的干扰总是在均值附近上下波动，为了得到频偏的无偏最小方差估计，可以对估计出来的频偏进行Kalman滤波。Kalman滤波是解决以最小均方误差为准则的最佳线性过滤问题，该算法根据前一个估计值和最近一个观测数据来估计信号的当前值[15]。Kalman滤波算法由状态空间来描述，其递推公式如下所示[16-17]。其状态预测为：

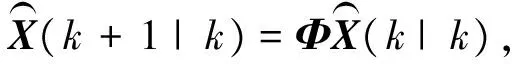
(12)

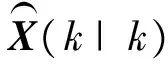
P(k+1|k)=ΦP(k|k)ΦT+ΓQΓT，

(13)

式中，P(k|k)为k时刻协方差阵值；P(k+1|k)为k+1时刻协方差阵的预测值；Γ为噪声驱动矩阵；Q为状态向量的噪声方差阵。k+1时刻的状态值为：

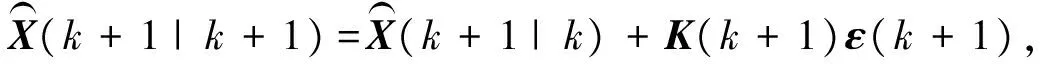
(14)

式中，

K(k+1)=P(k+1|k)HT[HP(k+1|k)HT+R]-1，

(15)

(16)

式中，Y(k+1)是k+1时刻的观测值；H为观测矩阵；R为观测向量的噪声方差阵。k+1时刻的协方差阵值为

P(k+1|k+1)=[In-K(k+1)H]P(k+1|k)，

(17)

式中，In为单位阵，表示系统状态的维数。通过上述的6个方程，可以准确地估计每一个状态值。在本文中把最大似然估计获得的频偏作为观测序列Y(k)，采用一阶Kalman滤波就可以实时地估计频偏的变化。如果Q和R与噪声的模型匹配，频偏估计就具有最小的滤波误差方差[15]。

结合Kalman滤波和最大似然的频偏估计算法的实现原理如图1所示。

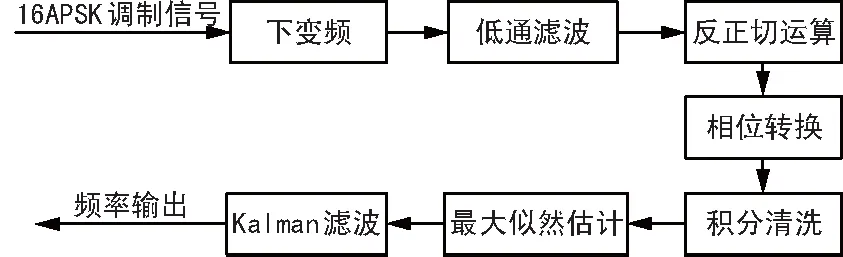
图1 结合Kalman滤波和最大似然的频偏估计原理

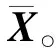
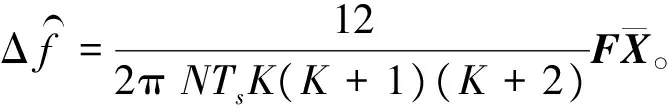
(18)

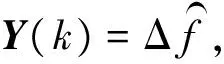
(19)

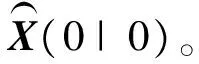
下面对结合Kalman滤波和最大似然的频偏估计算法进行仿真验证和分析。

4 仿真结果与分析

对结合Kalman滤波和最大似然的频偏估计算法进行Matlab仿真。测试信号为16APSK调制信号，码速率为1 MHz，采样频率为56 MHz，接收机本振的频率为70 MHz。从式(18)可以看出，影响最大似然频偏估计值的参数有K、N和F，在实验中K取值为8，N取值为20。

假设接收信号载波频率为70.1 MHz，即接收机本振频率与接收信号载波频率的固定偏差为100 kHz。仿真中，信噪比SNR变化范围为-5～30 dB。在不同的信噪比条件下，对最大似然估计算法和结合Kalman滤波的最大似然估计算法进行了仿真，仿真结果如图2和图3所示。

图2 不同信噪比下的频率估计的偏差

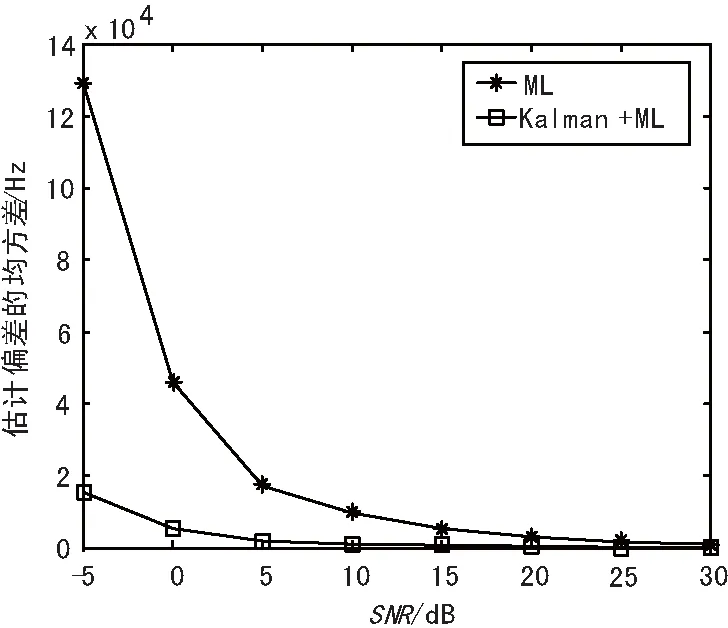
图3 不同信噪比下的频率估计偏差的均方差

图2反映的是不同信噪比条件下，估计得到的频偏和实际频偏的偏差值。频率估计偏差值的计算公式为：

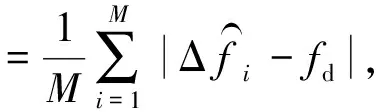
(20)

式中，fd为实际频偏值；M=2 000，表示2 000次估计样本。考虑到Kalman滤波初始状态的不确定性，先获得10 000次估计样本，把最新的2 000次估计样本作为衡量估计偏差值的样本。图3反映的是不同信噪比条件下，估计偏差值的均方差。频率估计偏差值的均方差计算公式为：

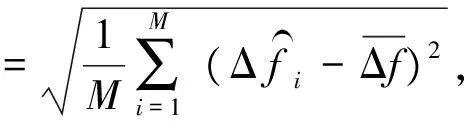
(21)

从图2可以看出，不同信噪比条件下，最大似然估计算法和结合Kalman滤波的最大似然估计算法获得频偏值相差不多，信噪比越高，估计的偏差越小。当在低信噪比条件下(SNR=-5 dB)，2种算法估计的频率偏差跟实际的频率偏差(100 kHz)都相差大约21 kHz，信噪比在0 dB时偏差可以达到2 kHz左右。从图3可以看出，2种算法估计的频率偏差的均方差都随着信噪比的提高而减小，相比最大似然估计算法，结合Kalman滤波的最大似然估计算法获得的频率偏差的均方差更小，即估计的频率值更稳定。当SNR=-5 dB时，最大似然估计算法估计的频率偏差值均方差为130 kHz左右，波动范围非常大；结合Kalman滤波的最大似然估计算法估计的频率偏差值均方差大约为15 kHz。在其他信噪比条件下，结合Kalman滤波的最大似然估计算法相比单独的最大似然估计算法估计的频率值均方差也都较小。2种算法频率估计偏差平均值相差不多，但结合Kalman滤波的最大似然估计算法在频率估计偏差的均方差性能上有较大改善，即结合Kalman滤波的最大似然估计算法估计的频率值更稳定。

以上是对固定载波频差信号的仿真，下面对含多普勒载波频偏的信号进行仿真。假设接收信号载波频率与接收机本振频率的偏差从100 Hz变化到100 kHz，步进为100 Hz。仿真中，SNR=-5 dB。仿真结果如图4和图5所示。图4反映的是在SNR=-5 dB时，2种估计算法对多普勒频偏的实时估计值。从图4可以看出，在低信噪比时，结合Kalman滤波的最大似然估计算法相比单独的最大似然估计算法估计的频偏值更接近真实的频偏值，能更好地抑制噪声引起的波动。图5反映的是在SNR=-5 dB时，2种算法估计的多普勒频偏和真实频偏的偏差。从图5可以看出，相比最大似然估计算法，结合Kalman滤波的最大似然估计算法估计的多普勒频偏值和真实频偏值的偏差小很多，结合Kalman滤波的最大似然估计算法估计的频偏值能更稳定地跟踪接收信号中真实的多普勒频移。

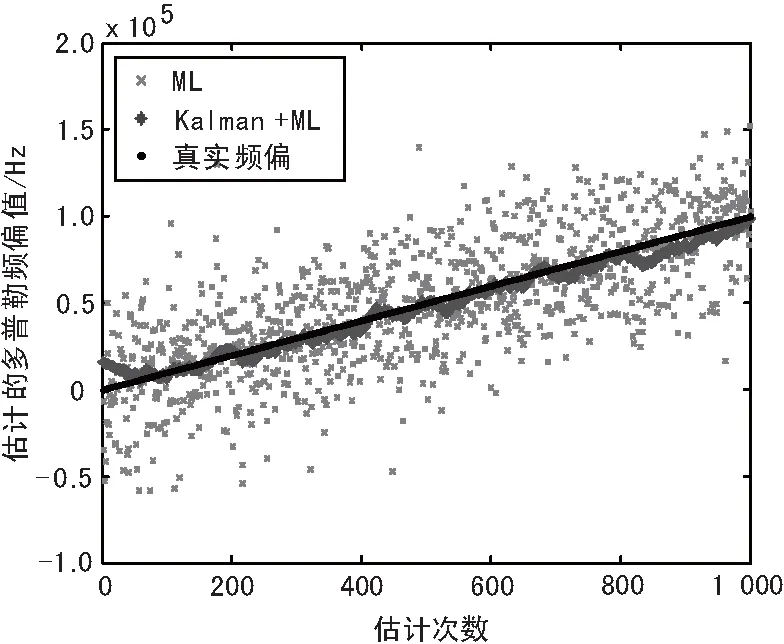
图4 SNR=-5 dB时估计的实时多普勒频偏值

图5 SNR=-5 dB时估计的多普勒频偏的偏差值

仿真结果表明，结合Kalman滤波的最大似然估计算法比单独的最大似然估计算法在频偏估计的精确度上有较大的改善。

5 结束语

本文讨论了一种基于Kalman滤波结合最大似然估计的16APSK频偏捕获算法。该算法是开环结构，实现简单，计算量小。仿真结果表明，相比最大似然估计算法，结合Kalman滤波的最大似然估计算法在载波的频偏估计偏差精度方面有较大的提高。该算法不仅适用于16APSK信号的频偏估计，也适用其他体制信号的非数据辅助的频偏估计。该算法具有较好的工程应用前景，对低信噪比条件下信号快速捕获的实际应用具有一定的参考价值。

[1] MORELLO A，MIGNONE V.DVB-S2：the Second Generation Standard for Satellite Broad-band Services [J].Proceedings of the IEEE，2006，24(1)：210-227.

[2] 梅凡.卫星数传系统中16APSK调制解调技术研究[D].北京：中国科学院国家空间科学中心，2016.

[3] 陈荣，周旭，张士强.扩频信号的捕获与跟踪[J].无线电工程，2010，40(5)：33-35.

[4] 段勇存，王力男，裴文端.一种机载卫星通信终端频率捕获跟踪算法[J].无线电通信技术，2016，42(3)：33-36.

[5] 何朝玉，李超，陈晖，等.一种适用于突发16APSK信号的载波同步算法[J].无线电工程，2012，42(5)：61-64.

[6] 刘晓冬，陈卫东.一种宽范围高精度的载波频偏估计算法[J].无线电工程，2014，40(3)：43-45.

[7] FRANTZESKAKIS E，KOUKOULAS P.Phase Domain Maximum Likelihood Carrier Recovery：Framework and Application in Wireless TDMA Systems [J].IEEE VTS 50th Vehicular Technology Conference，1999(5)：2571-2575.

[8] 王晓湘，柯有安.高动态多普勒频率的最大似然估计器[J].北京邮电大学学报，2000，23(1)：61-65.

[9] 唐金花，陈偕雄.一种基于最大似然估计的频偏估计算法[J].科技通报，2006，22(2)：263-266.

[10] 王乐，王竹刚，熊蔚明.基于最大似然频率精细估计的载波捕获算法[J].电讯技术，2013，53(1)：39-43.

[11] 王鹏宇，吕善伟.Kalman滤波在频率估计中的应用与仿真[J].宇航计测技术，2008，28(5)：23-26.

[12] 田甜，安建平，薛斌，等.基于最大似然估计和Kalman滤波的BPSK载波同步方法[J].北京理工大学学报，2012，32(1)：67-71.

[13] 崔霞霞，江会娟，万明刚.一种8PSK、16APSK与32APSK软解映射的实现技术[J].无线电工程，2011，41(4)：45-48.

[14] 杜勇.数字通信同步技术的MATLAB与FPGA实现[M].北京：电子工业出版社，2015.

[15] 吴迪松，张公礼，郑国.一种高阶QAM信号载波频偏估计算法[J].电讯技术，2006(4)：144-148.

[16] 黄小平，王岩.卡尔曼滤波原理及应用[M].北京：电子工业出版社，2017.

[17] 袁建国，马骏，李璋超.CO-OFDM系统中基于卡尔曼滤波对相位噪声补偿算法的研究[J].半导体光电，2015(6)：959-963.

[18] 曾富华，汪远玲，杨万麟.一种基于扩展卡尔曼滤波器的频率及频率斜率估计算法[J].电讯技术，2008，48(3)：70-73.