江中海上大跨越输电塔的船舶撞击响应分析及撞击力简化公式
贾兴隆, 张大长, 倪辉辉
(1. 南京工业大学 土木工程学院, 江苏 南京 211816;2. 江苏省住房和城乡建设厅, 江苏 南京 210036)
跨越江河、近海中的大跨越输电线路铁塔,在服役期内极易受到通航船舶的撞击作用。大跨越输电塔结构作为一种高耸结构,具有高度高、重量轻、刚度较小、外形细长等特点。限于大跨越输电塔自身质量和刚度分布特征,横向荷载在大多数情况下是其设计控制荷载,船舶撞击作用力是横向荷载的一种,但是目前关于船舶撞击大跨越输电塔的动力响应分析以及撞击力分析很少。
近年来,刘建成等[1]基于整船整桥碰撞数值仿真,提出有限元法可以比较精细地再现结构内部动力学过程,并对船桥碰撞力和能量转化的整个时间历程进行全面细致的模拟再现。Travanca J等[2]建议货轮船艏内部由于结构复杂,存在着许多加劲板件,为了简化模型,将加劲板以截面性质等效至主要板件厚度中,全船采用壳单元。张景峰等[3]提出了船舶船艏刚度不同则会导致碰撞力及桥梁结构响应的动力反应系数均存在较大差异。另外,涉及船撞力的国内外的规范和标准都是针对船舶撞击桥墩所得来的,如美国AASHTO规范、欧洲规范、我国铁路规范和公路桥涵规范[4~6],以上规范计算方法不同,考虑的影响因素不同,同时大跨越输电塔是一种高柔结构,不同于一般的桥梁结构,现有规范在此不完全适用。因此如何考虑船舶的撞击作用以及输电塔受船舶撞击作用后的撞击反应是目前亟须解决的问题。
本文综合考虑大跨越输电塔上部结构与下部高桩承台基础的相互作用,运用有限元软件ANSYS/LS-DYNA建立船舶撞击输电塔的简化模型,分析船舶质量、船舶速度、船艏刚度对撞击力的影响以及大跨越输电塔的位移响应特性;同时,开展船舶撞击大跨越输电塔的撞击力计算理论研究,撞击力的理论计算值与现有规范值进行对比,提出一个撞击力的简化计算公式,从而为工程设计提供参考依据。
1 大跨越输电塔及撞击分析模型
1.1 大跨越输电塔及基础设计参数
本文以某江中大跨越输电塔为原型[7],杆塔塔身总高(z轴)约370 m,杆塔在水平面关于x,y方向轴对称,塔腿根开均为51.62 m,塔身钢材采用Q345。高桩承台基础的平面为60.62 m×60.62 m的正方形,承台底面高程高于设计水位线之上;板式承台下为群桩基础,桩长为50 m。
1.2 撞击船舶参数
撞击船舶为在役船舶[8],航道选择为长江下游段,可通航3~5万吨级船舶,船舶主要尺寸参数见表1。

表1 撞击船的主尺度 m
1.3 撞击模型及分析方法
采用有限元模拟的分析方法,建立船舶撞击大跨越输电塔的三维模型;模拟分析船舶撞击大跨越塔承台基础,即沿x方向撞击船艏撞击承台侧面(塔腿1所在位置),船艏与承台发生碰撞。因此,网格划分时船艏的网格划分相对精细,船身网格相对粗一些[9]。大跨越输电塔及船舶模型如图1所示,分析模型参数见表2。

图1 船舶及大跨越输电塔模型

结构类型单元类型材料类型E/MPaνρ/(t·mm-3)T/MPafy/MPa塔架BEAM161弹性2.00×1050.37.80×10-9承台SOLID164弹性2.00×1040.22.40×10-9桩BEAM161弹性2.00×1040.22.40×10-9船艏SHEEL181线性强化弹塑性2.00×1050.37.80×10-92.00×1033.45×102船身SHEEL181刚性0.37.80×10-9
注:E为钢材弹性模量;ν为钢材泊松比;ρ为钢材密度;T为钢材剪切模量;fy为钢材强度设计值
船舶撞击承台时,需定义船艏和承台接触面,接触面能有效地模拟相撞结构之间的相互作用,并允许结构之间连续不断的接触和滑移。采用自动面-面接触(ASTS)类型,静、动摩擦系数均采用0.3[10],船艏结构为接触面,承台结构为目标面。
1.4 边界条件
有限元模型中桩基础底部采用固结形式,建模时为了方便计算不考虑水的影响。跨越塔x方向为横担方向;y方向为顺线路方向;z方向以竖直向上为正。
2 船舶撞击模拟分析
2.1 跨越塔位移响应特性
(1)跨越塔不同高度处的水平响应
选取大跨越塔不同部位:塔腿根部(节点4),1/2塔高(节点351),塔顶(节点973),节点选择如图2a所示。

图2 节点选取示意
塔身节点x,y方向位移-时程曲线如图3,4所示,从图3,4可知,大跨越输电塔受到船舶撞击作用后,x,y方向均出现撞击响应,并以x方向的撞击响应为主。塔身x方向随着高度的增加,振幅逐渐增大;塔身y方向随着高度的增加,振幅逐渐减小;同时从图中可以看出同一节点处的x,y向的振动周期是一样的,而且不同塔身部位的x,y向位移多处出现反向,说明输电塔在受到船舶撞击后,在高度方向上出现弯曲变形,发生了二阶弯曲。

图3 塔身节点x方向位移-时程曲线

图4 塔身节点y方向位移-时程曲线
(2)跨越塔的扭转响应
如图2b所示,选取大跨越塔四个塔腿根部典型节点:塔腿1(节点4)、塔腿2(节点8)、塔腿3(节点93)和塔腿4(节点114),考察其撞击响应。
跨越塔典型部位的撞击响应如图5所示,x轴线上的塔腿(1和2,3和4)协同变形,位移基本一致;从图6可知,y轴线上的塔腿(1和3,2和4)协同变形,位移基本一致;两轴线上塔腿节点的幅值相同,但振动方向相反,说明输电塔在某一塔腿受到船舶正向撞击后在水平面上发生了扭转振动。

图5 塔腿节点x方向位移-时程曲线

图6 塔腿节点y方向位移-时程曲线
(3)大跨越输电塔塔身振动变形
船舶撞击大跨越输电塔后,振动响应由塔身底部传至塔顶部,选取输电塔几个时间点的振动变形如图7所示。图7a显示撞击刚开始时塔身下部反映强烈,逐渐传至塔顶,塔身为S型弯曲变形;图7b,7c为撞击过程中塔身的变形,表现为一阶弯曲变形;图7d表示撞击发生后输电塔整体结构发生了扭转,高桩承台处扭转最为强烈。

图7 大跨越输电塔振动变形
2.2 撞击力-时程曲线特性
船舶质量为9000,11250,13500 t并以4 m/s的速度撞击跨越塔时,分析得到的撞击力-时程曲线如图8所示,撞击力时程参数如表3。随着船舶质量增加,最大撞击力增加,撞击持续时间也在增加,不同质量作用下撞击力-时程曲线形式仍然保持一致。当撞击发生后,撞击力迅速达到最大值,此后又迅速降低,而且在撞击过程中还发生多次重复撞击,即多次能量交换。
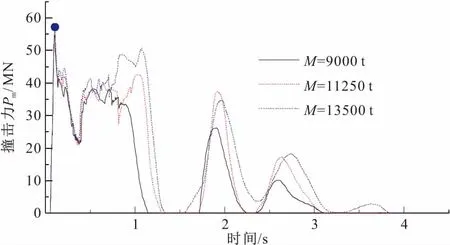
图8 撞击力-时程曲线
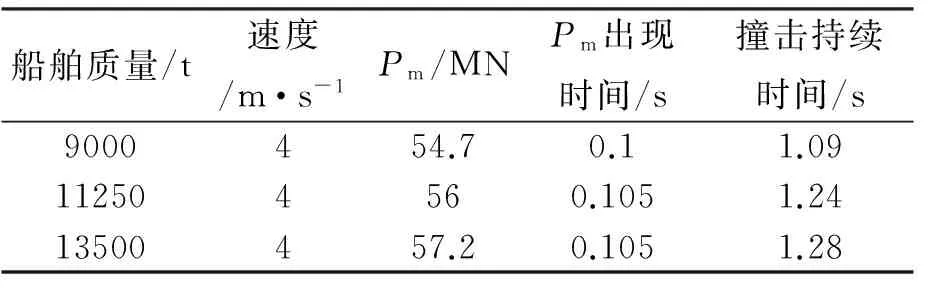
船舶质量/t速度/m·s-1Pm/MNPm出现时间/s撞击持续时间/s9000454.70.11.09112504560.1051.2413500457.20.1051.28
2.3 失效模式
船舶碰撞是一种复杂的非线性动态响应过程,碰撞区局部迅速超越弹性阶段而进入塑性阶段,并可能发生局部撕裂、屈曲等多种形式的破坏或失效[11]。
因此,本文以船头钢板撞击出现局部屈曲为失效准则,即当撞击时船艏钢板破坏强度超过钢材强度设计值时,认为达到破坏。
2.4 撞击过程中的能量转化规律
撞击过程是把船舶动能转化为结构振动能量的过程,体系过程遵守能量守恒定律,总能量由船舶动能提供,能量转化曲线如图9所示。从图9曲线可以看出,撞击开始时船舶动能快速转化为船舶内能、结构动能和结构内能,以及接触过程中损失的一部分能量,船舶与输电塔撞击回弹后获得剩余动能;结构自振过程中由于结构自身的耗能性能,体系的总能量不断损失,自振过程中结构能量在内能和动能之间不断转化,通过弹塑性变形得到耗散。
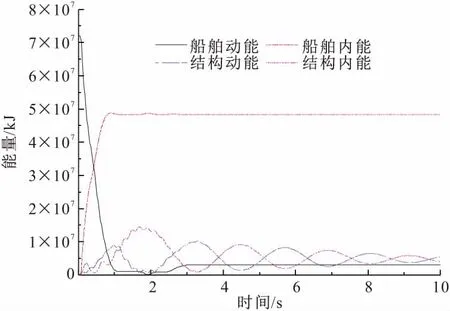
图9 撞击过程中能量转化曲线
3 撞击力计算理论
3.1 影响因素
(1)分析参数
本文考虑船舶质量M、速度v、船头刚度(厚度)t对撞击力的影响。具体参数见表4。

表4 有限元分析参数
(2)船艏刚度的影响参数分析
为研究船艏刚度的变化对撞击力的影响,建立一个半径为6 m的半球面模型模拟船艏,半球面材料模型和船艏材料模型一致。选取钢板厚度分别为40,50,60,70,80 mm,船艏模型和半球面模型分别如图10a和10b所示。
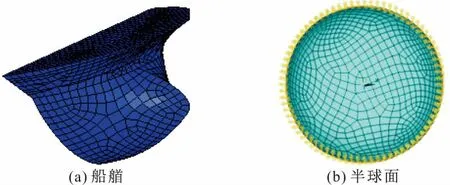
图10 船艏和半球面模型
撞击模拟得到半球面变形及船艏变形分别如图11a,11b所示,可以看出两者破坏形式大致相同,圆球面变形主要集中在位移最大处,向内凹陷,撞击接触区发生屈曲破坏;船艏结构发生类似破坏,可以认为用圆球面模拟船艏结构的方法是可行的。
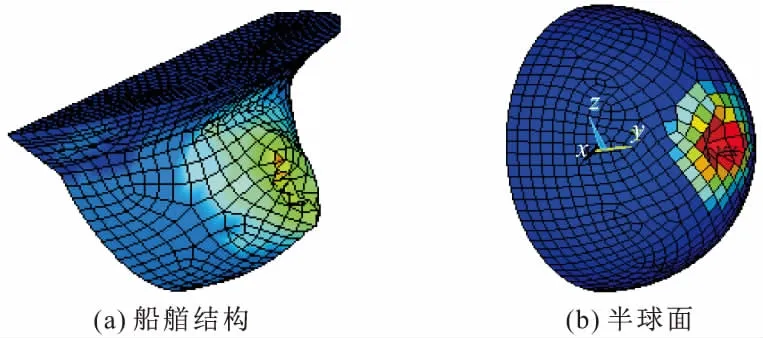
图11 船艏结构和半球面变形
随着钢板厚度的增加,钢板所承受的极限荷载增加,同时达到破坏时的位移增加。因此,圆弧面所承受的极限刚度亦增加,如表5所示。

表5 各个参数下的极限刚度
采用曲线拟合的方法分析圆弧面钢板刚度计算方法,得到参数a=7599,b=1333,c=0.6983;曲线相关系数为0.9971,即圆弧面钢板刚度K与厚度t的关系式为:
K=7599×t2+1333×t+0.7
(1)

图12 钢板厚度与极限刚度关系
3.2 撞击力计算理论分析
不同撞击船舶质量、撞击速度下,模拟分析得到的最大撞击力如表6所示。

表6 各参数作用下的最大撞击力Pm MN
(1)船舶速度
船舶质量一定时,最大撞击力随速度变化的曲线如图13所示,各种吨位船舶的最大撞击荷载随着撞击速度的增大而增大,两者之间成非线性增长关系,采用二次抛物线方程:
Pm=A×v2+B×v+C
(2)
式中:Pm为船舶最大撞击力(MN);v为船舶撞击速度(m/s);A,B,C为最大撞击力与船舶速度的相关系数。不同Pm-v关系对比如表7所示。

图13 Pm-v关系曲线

船舶质量/tABCR67501.33-5.452.120.993790001.50-4.850.061112501.77-6.1152.720.9997135002.15-6.3151.390.9947157502.44-5.4949.290.991618000均值2.822-5.25-5.5647.5850.530.9902
注:R为相关系数
(2)船舶质量
根据表6的分析结果,速度一定时,最大撞击力随船舶质量变化的关系曲线如图14所示,不同速度作用下的最大撞击力随船舶质量的增大而增大,两者之间成非线性增长关系,采用幂函数[12]方程:
Pm=a×Mb
(3)
同时质量越大,撞击持续时间越长。
最大撞击力与质量M关系如表8所示,按上述思路进行数值拟合,最大撞击力与船舶质量或吨位在各种速度下有较好的相关性。

图14 Pm-M关系曲线
不同速度所对应的a值如表9所示,指数b为与速度无关的量。由于最大撞击力与船舶质量的函数表达式中必然包含一个与速度有关的量,故系数a应该是与速度有关的,拟合得到a值与对应速度的关系曲线如图15所示,系数a并不与速度成线性关系,而是类似于二次抛物线的形式。因此,用函数来代表二者的关系,运用曲线拟合得到的相关参数值如表7。

表8 最大撞击力与M关系计算结果
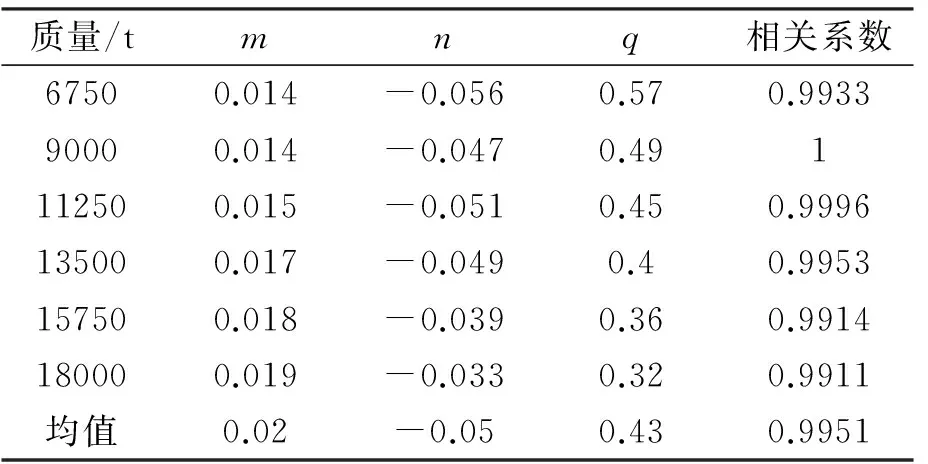
表9 v-a参数计算结果

图15 v-a关系曲线
经过以上的拟合和简化过程,最大撞击力与船舶质量和速度的关系式为:
Pm=(0.02×v2-0.05×v+0.43)×M0.51
(4)
当撞击速度为1m/s时,随着船舶质量的增加,最大撞击力逐渐增加,但是质量为13500t时,最大撞击力为46.06MN,之后最大撞击力增加缓慢,基本上趋于稳定,当质量为50000t时,最大撞击力为50.59MN。通过观察船艏结构应力云图,发现质量达到13500t时,船艏模型基本趋于破坏。因此认为,当船舶质量为(15000-50000)t时,最大撞击力基本不变,取47.1MN。
(3)船艏刚度
建立质量为10000t船舶以4m/s的速度撞击跨越塔,采用改变船艏钢板厚度来实现船艏刚度的变化,分析30,40,50,60,70,80mm六个钢板厚度参数,得到各个参数对应的撞击力Pm1,同时用公式(4)计算得到撞击力Pm2,相关数据见表10。
计算值和模拟值的比值如表10所示,最大撞击力随着船艏刚度的变化而变化,如图16所示,两者呈线性关系;因此,公式(4)前面应该有一个相对应的参数α与船艏刚度有关,假设两者的关系式为:
α=R×t+S
(5)
运用曲线拟合得到R=26.1,S=-0.32,相关系数为0.9803。

表10 刚度影响相关数据

图16 Pm1/Pm2与钢板厚度关系
因此,最大撞击力与船舶质量、撞击速度、船艏刚度的关系式为:
Pm=α×β×M0.4
(6)
式中:α与船艏刚度有关,且α=26.1×t-0.32,其中t为船艏钢板厚度(m);β与撞击速度有关,且β=0.02×v2-0.05×v+0.43,v为撞击速度(m/s);M为船舶质量(t)。
(4)撞击力简化公式的误差分析和适用条件
撞击力简化公式是基于有限元数据分析提出的,通过理论值与计算值的对比发现,当速度为2~6 m/s时,误差控制在10%左右;当速度为6~8 m/s时,误差相对偏大,达到了15%~20%。
针对本文的分析情况,简化计算式的适用条件如下:
(1)船舶正向撞击输电塔结构;
(2)撞击速度为2~8 m/s;
(3)船艏钢板厚度为0.02~0.08 m;
(4)吨位为30000 t以下船舶。
3.3 撞击力计算公式与现有计算规范比较
船撞力简化计算式(6)与AASHTO规范、欧洲规范、我国铁路规范以及公路桥涵规范公式的对比计算结果[13]如图17所示,撞击速度从2 m/s变化到8 m/s。从图中可以看出,撞击速度发生变化时,对于同一吨位的船舶,各船撞力式计算出的结果差别较大。当撞击速度为2 m/s时,式(6)Pm的计算值与欧洲规范值较为接近,二者之间最大相差2%;当撞击速度为2~8m/s时,式(6)Pm的计算值要明显小于欧洲规范值,但与AASHTO规范值比较接近;当船舶撞击持续时间均取1s时,公路桥涵规范计算值在铁路规范和欧洲规范值之间波动,随着船舶质量的增加,公路桥涵规范计算值逐渐向欧洲规范值靠近;在所有船撞力计算值的比较中,我国铁路规范的计算值是最小的,这在工程应用中显得太过保守,不利于工程施工。

图17 各船撞力公式计算结果对比
4 结 论
基于上述模拟分析和计算,可以得到如下主要结论:
(1)船舶撞击大跨越输电塔时产生的撞击力作用时间短、荷载大小变化剧烈;同时,船舶撞击过程中发生多次重复撞击。
(2)船舶撞击江中海上大跨越输电塔时,整体结构在x,y方向均出现撞击响应,并以x方向的撞击响应为主;同时,大跨越输电塔基础在y方向发生一定的扭转振动。
(3)船舶撞击作用下,高桩承台基础的变形较为显著,跨越塔沿塔身高度方向上表现出弯曲变形。
(4)船舶撞击力随着船舶质量及撞击速度的增加呈非线性增长,而随船艏刚度的增加呈线性增长;同时,本文所建议的计算公式值与模拟值更为吻合,可为工程设计提供参考依据。
[1] 刘建成, 顾永宁. 基于整船整桥模型的船桥碰撞数值仿真[J]. 工程力学, 2003, 20(5): 155-162.
[2] Travanca J, Hao H. Energy dissipation in high-energy ship-offshore jacket platform collisions[J]. Marine Structures, 2015, 40: 1-37.
[3] 张景峰, 李小珍, 肖 林, 等. 两类船-桥碰撞力差异及桥梁结构响应分析[J]. 振动与冲击, 2016, 35(4), 156-161.
[4] TB 10002.1-2005, 铁路桥涵设计基本规范[S].
[5] 辛济平, 万国朝, 张 文, 等. 美国公路桥梁设计规范[M]. 北京: 人民交通出版社, 1994.
[6] JTG D60-2004, 公路桥涵设计通用规范[S].
[7] 倪辉辉. 江中大跨越输电塔结构撞击反应及其模型试验设计方法[D]. 南京: 南京工业大学, 2015.
[8] 谢永和, 吴剑国, 李俊来. 船舶结构设计[M]. 上海: 上海交通大学出版社, 2011.
[9] 李艳贞. 船舶与海上风电站碰撞的数值仿真研究[D]. 上海: 上海交通大学, 2010.
[10]熊安平. 基于LS-DYNA仿真模拟对船桥撞击的研究[D]. 南昌: 华东交通大学, 2012.
[11]Paik J K, Pedersen P T. Modelling of the internal mechanics in ship collisions[J]. Ocean Engineering, 1996, 23(2): 107-142.
[12]陈 诚. 桥梁设计船撞力及损伤状态仿真研究[D]. 上海: 同济大学, 2006.
[13]王君杰, 颜海泉, 钱 铧. 基于碰撞仿真的桥梁船撞力规范公式的比较研究[J]. 公路交通科技, 2006, 23(2): 68-83.

