换热器微细通道纳米流体沸腾混沌特征与强化传热的关系
罗小平,郭 峰,王 文,廖政标
0 引 言
微通道纳米流体沸腾传热技术可以实现极高的换热强度,在航空航天、农业工程机械、微电子、生物制药等领域都得到了广泛的应用[1-2]。目前学者多采用牛顿冷却定理、量纲分析法来对相关问题进行研究[3]。Yu等[4]以 Al2O3-水为工质进行了微通道内的流动沸腾试验并利用牛顿冷却定理进行了相关的推导计算,发现相较纯水而言,纳米流体的沸腾起始点出现的更早,流动的稳定性有所增强,传热系数也有一定提升,并认为这种情况的出现是由纳米颗粒的沉积造成的。Wan等[5]以Cu-水纳米流体为工质进行试验,发现质量分数为1%的纳米流体使得壁面过热度降低了12.8%,传热系数提高了19.5%,认为存在一个最佳纳米颗粒浓度,能够最大强化传热,其试验条件下最佳纳米颗粒质量分数为1.5%。Li等[6]则对现有的研究进行总结,将纳米颗粒沉降对表面性能的影响与传热关联式联系了起来,通过对传热影响较大的因素无量纲化,建立了纳米流体沸腾传热系数的经验关联式,有效提升了预测模型的准确性。Prajapati等[7]制成ZnO-H2O纳米流体进行试验,其中纳米颗粒ZnO质量分数在0.000 1%~0.1%范围内,发现与纯水相比,纳米流体能使沸腾传热系数提升126%;在较低的纳米颗粒浓度下,压降变化并不明显,而在纳米颗粒浓度为0.1%时,压降增加了23%。
以上学者的研究都是通过试验总结出纳米流体传热特性与纳米粒子浓度、热流密度、质量通量等参数的定性关系,并在试验数据的基础上拟合出换热关联式。然而微通道内的流动沸腾作为一种汽液两相流,包含了众多沸腾汽泡的生成、长大和脱离以及相互作用等系列子过程,属于复杂的非线性系统[8],向制冷剂中添加纳米级颗粒后,其过程将更加复杂,采用传统分析手段难以对其动力学特性进行准确描述。一些学者采用分形理论、关联维数、Lyapunov数及Kolmogorov熵等非线性分析手段对沸腾传热的非线性特征进行了研究[9-10]。强爱红等[11]通过采集常规通道内汽液固三相流动沸腾过程中的温度信号建立单变量时间序列,并运用相图等非线性分析手段发现此类系统具有混沌特征且颗粒体积分数越大,非线性特征量越大,传热系数也越大。Langford等[12]计算了垂直上升管内空气-水两相流压力波动的 Kolmogorov熵和关联维数, 表明 Kolmogorov 熵会随着折算气速和折算液速的变化而改变。Gavilán-Moreno等[13]利用电压信号时间序列研究了沸水堆运行的非线性特征,利用相空间重构还原了系统的动力学特征,揭示了该系统的混沌特性,提出了沸水堆稳定运行的工况条件。Jin等[14]研究了单管流动沸腾过程中折算液速随时间的波动情况,发现其具有低频高幅振荡的特点,并根据波动图重建了沸腾系统的动力学特征,发现该系统具有混沌的特性。贾涛等[15]对核态沸腾传热试验中不同工况下汽化核心处的温度时间序列进行了非线性研究,重建了这些温度时间序列对应的三维吸引子,并从三维吸引子中求出关联维数和相应的最大Lyapunov数,结果表明,汽化核心处的温度时间序列具有混沌的特征。
以上都是针对常规大通道流动沸腾状况的研究,对于微细通道来说,由于通道尺寸的限制,惯性力作用减弱,表面张力影响增强,流动沸腾状况与常规通道相比有较大不同,从非线性分析的思想出发,研究微细通道内纳米流体沸腾传热的非线性特征,对准确描述该系统的动力学特征有着十分重要的意义。因此,本文根据以上研究成果,进行纳米流体在2 mm×2 mm矩形微细通道内的流动沸腾试验,通过采集试验段进出口的压差数据,建立单变量时间序列,利用Hurst指数、关联维数、最大Lyapunov数和Kolmogorov熵,定量研究其非线性特征量与流动沸腾传热效率的关系,从而进一步揭示纳米流体强化相变传热的机理。
1 试验设计
1.1 试验系统及相关装置
本文采用实验室自行设计的微细通道试验平台进行流动沸腾试验,平台如图 1所示。试验开始时,工质由注液器注入系统,待试验段出口压力值达到预定值时,关闭注液口阀门,使系统处于封闭状态,开启磁力泵,使工质在整个封闭系统中循环运行。纳米流体经过预热器预热到既定温度,然后以液态向上流入试验段,试验段底部设置有加热板,对微细通道进行加热,工质在试验段经过流动沸腾后,以汽液两相状态从出口流出,经冷凝器冷凝后,又返回磁力泵,完成一个循环并开始下一个循环。
微细通道采用 6063-T5铝材料经电火花线切割加工而成,整个试验段共设置12个微细通道,单个通道尺寸为2 mm×2 mm,通道长240 mm。试验前用2 000#砂纸(尺寸范围在2.0~1.5 μm)对通道表面进行打磨,并放置在超声波振荡仪中用去离子水进行震荡清洗,以除去表面的氧化膜及残渣。
本试验所用磁力泵(型号20LH0-12,广州隆鑫泵业有限公司生产)最大输出流量为3 m3/h,额定功率0.37 kW,扬程12 m。试验时利用FR-D720S-2.2K-CHT型变频器对泵出口流量进行变频控制,从而满足试验多工况的要求,变频器额定功率为2.2 kW,输出频率为0.2~400 Hz。加热装置选用不锈钢云母加热板为热源,同时使用TDGC2-3KVA型调压器调整输出功率,试验时通过旋转调压器顶部的旋钮控制其输出电压,控制加热板的输出功率,从而调节试验段通过的热流密度并研究不同热流密度对微通道内两相流动沸腾传热特性的影响。其中加热板规格为220 V/1 500 W,调压器电压调节范围为0~250 V。试验系统内流量的调节则利用LWGY系列涡轮流量传感器及相配套的流量计算仪来完成,其中流量传感器量程为0~250 L/h,精度为0.5%。

图1 微细通道流动沸腾试验系统Fig.1 Experimental system of flow boiling in micro-channels
1.2 数据采集
本文利用一段时间内的压差数据来建立单变量时间序列,所需压差数据由试验段入口压力减去相应时刻的出口压力而得,工质进出口的压力值则分别由设置在试验段进出口端的压力传感器测量,进出口压力测点相距240 mm,试验选择型号为HC3160-HVG4的压力变送器(量程范围为0~100 kPa,精度为0.5%),可将压力信号转化为1~5 V标准电压信号。整个试验段侧壁面另设置5对测温点,其中一对测进出口工质温度、另外4对测壁面温度(t1, t2, …, t8计算时分别表示为 Tup,1, Tdn,1, …,Tdn,4)。温度由型号为WRNK-191的K型热电偶(测量范围为 0~200 ℃,精度 0.2%)来进行测量,其中热电偶与MIK-ST-500温度变送器相连,可将所测量的温度信号转换为标准1~5 V电压信号。采用ADAM-6017研华数据采集模块对压力变送器和温度变送器的标准信号进行采集并将其传输至工控机,模块采集频率为5 Hz。图2为试验段结构及测温点与测压点的位置图。
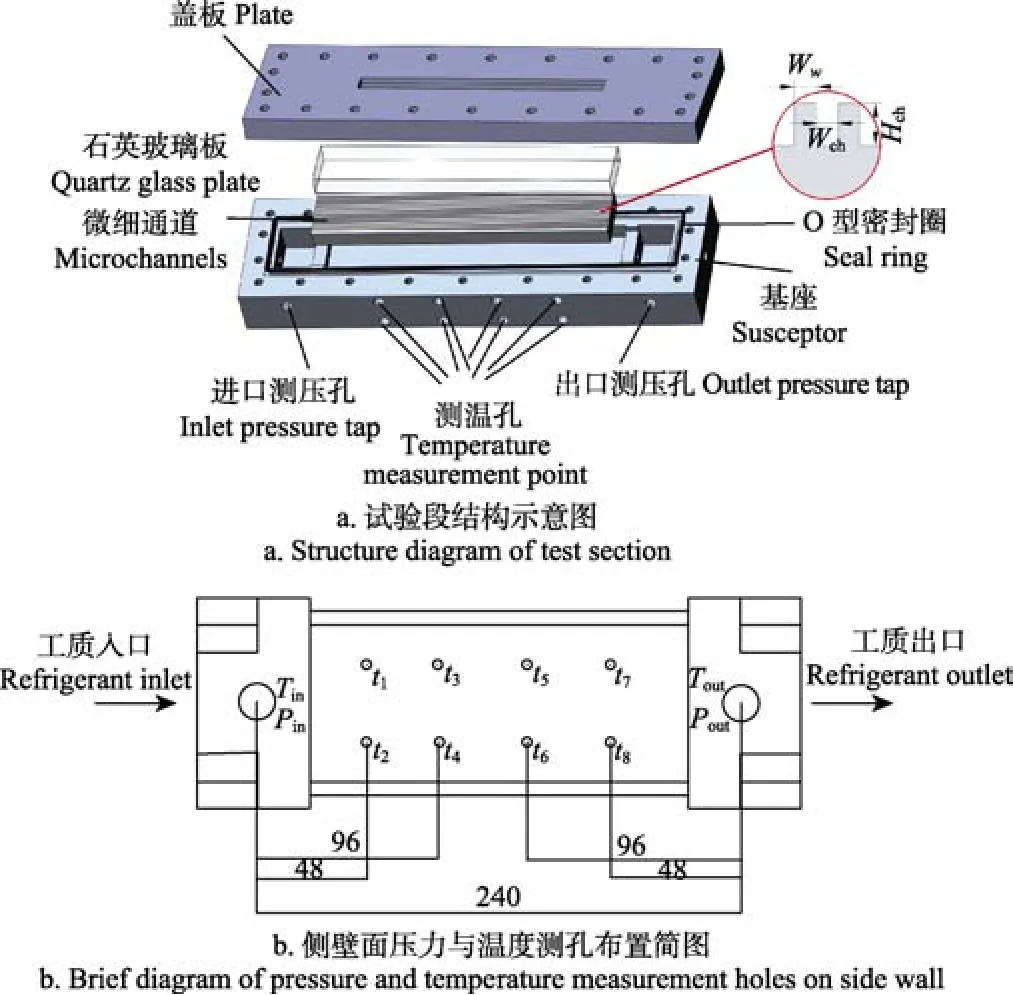
图2 试验段结构及测点布置Fig.2 Structure of test section and layout of measuring points
为提高测试结果的准确度,本文采用降温法对测试用压力传感器和热电偶在使用前进行了标定,选择温度标定范围为 20~90 ℃,先将水加热至 90 ℃以上,搅拌均匀,待水温降至90 ℃开始采集,之后每隔1 ℃采集1次,直至水温降低至20 ℃,停止标定,标定结果见表1。

表1 传感器标定结果Table 1 Results of sensor calibration
1.3 纳米制冷剂的制备
本试验纳米制冷剂选用 SH-A25型 Al2O3纳米颗粒(平均直径95 nm,扫描电镜(SEM)图像见图3a)与R141b纯制冷剂经两步法[16]配制而成,具体配制过程如图3b所示,为确保配制到浓度准确的纳米流体,采用上海恒平AE224分析天平(量程120 g,精度为0.1 mg)称量纳米颗粒。文献[17]表明该方法制得的纳米流体分散均匀并能在较长时间内保持稳定。根据本实验室以往的研究[18],低浓度的纳米流体有强化相变传热的效果,浓度过高反而会恶化传热,Al2O3/R141b纳米制冷剂质量分数低于 1%时,在微通道流动沸腾试验中的颗粒沉积量极少,且浓度越低性质越稳定,因此本文选择配制较低浓度的纳米制冷剂,所配制的纳米流体的质量分数分别为0.05%、0.10%、0.15%、0.20%和0.30%。

图3 纳米制冷剂的制备与检测Fig.3 Preparation and detection of nano-refrigerant
由于纳米颗粒的加入,纳米流体相对于其基液各物性参数发生了变化,本文参考文献[19]对其各物性进行计算,得到饱和温度46.9 ℃条件下,不同浓度纳米流体的物性参数见表 2。文献[20]通过该方法计算了纳米流体的物性参数,并与试验测试结果进行对比,发现计算结果与实测结果误差很小,证明了该计算方法的准确可靠。

表2 Al2O3/R141b纳米制冷剂流体物性参数Table 2 Physical parameters of Al2O3/R141b nano-refrigerant
为验证所配制的纳米流体具有稳定性,本文采用紫外可见分光光度计(型号agilent cary60,美国agilent公司生产)对其进行了透射比试验,所谓投射比是指透过材料或介质的光通量与入射通量之比,当一段时间后流体的透射比保持不变,即可证明该流体处于均匀稳定状态。试验结果如图3c所示,一段时间后不同浓度纳米制冷剂的透射比都趋于稳定,说明此时纳米制冷剂已经分散稳定。
1.4 试验方案
由于本文主要研究微细通道流动沸腾的非线性特征,为确保纳米流体在微细通道内达到核态沸腾,结合实验室以往的研究,本试验设计系统压力为165 kPa,在质量流量310.5 kg/(m2·s)条件下,分别进行了热流密度为14、18、22、26、30、34、38、42 和 46 kW/m29 种工况下的流动沸腾试验,为确保试验数据可靠,每组工况独立进行 2次试验,经验证以上工况范围可使纳米流体顺利进入核态沸腾阶段。
2 理论分析及数据处理
2.1 传热系数计算及误差分析
本试验温度范围内,6063-T5型铝材的导热系数λ几乎不变,而沿工质流动方向的热量传递忽略不计,因此热量沿着截面内厚度方向进行一维热传导,如图4所示。由Fourier导热定律[21]得第i对测温点(14i≤≤)所在截面局部有效热流密度,eiq

式中e,iq 为第i对测温点局部有效热流密度,W/m2;λ为铝材料的导热系数,W/(m·℃);Tup,i、Tdn,i分别为侧壁面第i对测温点处上、下端测点温度值,℃;δ为上下测温点距离,mm。
试验中,可认为沿着工质流动方向加热壁面热流均匀分布,故整体加热面的平均有效热流密度值qave为

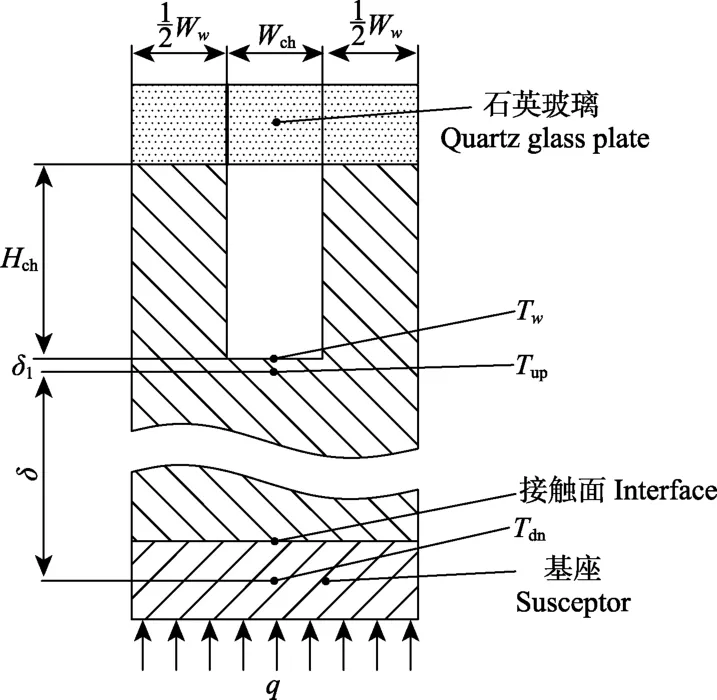
注:δ为上、下温度测点距离,mm;δ1为上测点距通道底面距离,mm;Tup、Tdn分别为测温点处上、下端测点温度值,℃;Tw为壁面温度,℃;q为热流密度,kW·m-2。Note: δ represents distance between top and bottom temperature measurement point, mm; δ1 represents distance between the bottom surface and the top measuring point, mm; Tup and Tdn respectively represent the temperature value of the top and down measuring points, ; ℃Tw represents the wall temperature, ℃; q represents heat flux density, kW·m-2.
通道底面温度Tw,i如下

测点处壁面过热度ΔTsat

式中Tsat为微通道内试验工质的饱和温度,℃。
传递给流体工质的热量来源有 2部分:一部分来自于槽道底面,另一部分来自于槽道两侧壁面。因此计算传热系数 h时,需考虑肋片效应带来的影响,本文使用Lee等[22]对矩形微细通道的两相流沸腾传热计算

故第i对测温点处局部传热系数hi为
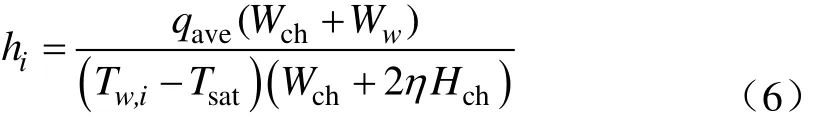
式中肋片效率η为
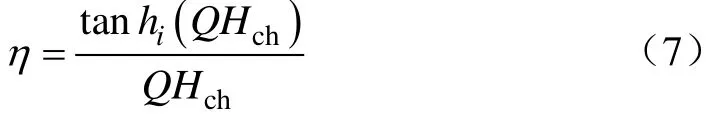
式中Q为肋片参数

整个微细通道流动沸腾的平均传热系数为

由式(7)、(8)、(9)可以看出传热系数与肋片参数互相耦合,故本文利用迭代的方法,通过MATLAB编程计算各值。
2.2 误差分析
本文将试验数据的误差分为 2类:直接测量参数误差和计算参数误差。
1)直接测量误差
直接经过仪器测量得到的试验参数主要有:主回路质量流量、试验段工质进出口压力、各壁面测温点温度及流道尺寸等,这些参数测量误差取决于测量仪器的精度。
2)计算参数误差
对于计算参数所带来的误差,采用误差传递理论[23-24]进行估算,对于计算参数Z,其由直接测量参数X1,X2,…Xn经计算得到

已知X1,X2,·· Xn的测量不确定度 δX1,δX2,… δXn,则Z的不确定度

相应的Z的相对不确定度为

2.3 Hurst指数分析
Hurst指数是一个用以研究“有偏随机游动”的统计量,被广泛用于时间序列的混沌分形分析,目前国内外许多学者将其应用于两相及多相流的分析[25]。当H=0.5,代表所研究的序列为完全随机序列;0.5 式中 n为样本长度;R/S为重标极差;C为常数;H为Hurst指数。 曲线斜率即为随机系列对应的Hurst指数值。 重构相空间理论认为由于非线性的相互作用,系统任一分量的演化是由与之相互作用着的其他分量所决定的,通过其一个特征分量即可重构出一个与原非线性空间相等价的状态空间,从而研究该系统的动力学特征。目前广泛采用延迟坐标法[27]来进行相空间重构,对于一个在时刻 ti=t0+iΔt时所对应的单变量时间序列 x(i)(i=1,2,…n) 式中 N=n–(m–1)τ,m 代表嵌入维数,τ称为延迟时间,通过确定恰当的 m和τ,即可将一个单变量时间序列扩展为一个m维的相空间,在拓扑等价的意义下恢复原来系统的动力学形态。 关联维数D2作为一种分形维数对系统的时间过程行为反应敏感,能够较好地反映系统的动力学特性,可用来衡量相空间中吸引子的复杂性,同时也是混沌识别的一种方法。G-P算法是定义和计算关联维数的经典方法[28]:给出任意小距离r,对于相空间中各点Xi(i=1,2N…),计算另外 N–1个点到它的距离,则可以统计出落于以点Xi为中心、以小标量r为半径的体积元中的点的个数,从而得到关联函数Cm(r) 式中H(x)为Heaviside阶跃函数 当r趋向于0时,存在 Cm(r ) ∝ rD2,则关联维数D2 计算关联维数时,首先画出一个嵌入维数下的双对数曲线lnCm(r)—lnr,取其中线性度较好的部分,对其进行最小二乘线性拟合,拟合直线的斜率即为对应嵌入维数下时间序列的关联维数,然后逐步增加嵌入维数 m,重复上述步骤,直到相应的D2值随着m的增大而在一定的误差范围内波动,此时得到的D2值即为该动力系统的关联维数。如果D2值随着m的增大而增大,并不收敛于一个稳定的值,则表明所研究的系统为随机时间序列。 混沌的一个重要特征是初值敏感性,即初始时刻相邻的点随着时间推移不断地分离,Lyapunov数即被用来定量的刻画这种敏感依赖性。对于k维混沌系统,分别存在从大到小的Lyapunov指数 λ1,λ2,…λk,在非线性动力学中,最大Lyapunov指数是区分混沌和非混沌行为的重要指标,最大Lyapunov指数的正、零和负分别表示系统处于混沌的、周期的和基本稳定的状态。本文采用小数据量法求最大Lyapunov指数[29],首先由快速傅里叶变换(fast fourier transform, FFT)法计算延迟时间和平均周期P,然后对系统进行相空间重构,找出相空间中每个点的最邻近点并限制其短暂分离,测量各个点的平均分离距离,最后用最小二乘法拟合出回归直线的斜率即为最大Lyapunov指数。 Kolmogorov熵简称K熵,是确定系统混沌程度的一个重要定量特征,是关于系统不确定性的度量,它可以通过测量信息的丢失速率,进而表征系统的可预测度。对于随机行为,完全不可预测,故K熵是无界的;对于周期行为,系统的后续演化完全可以预测,K熵为零;对于混沌行为,K熵则是一个大于零的有限值,且数值越大,表明系统越混沌。 对于Kolmogorov熵的计算,本文根据文献[30],通过K2熵逼近法来实现 图 5为不同浓度纳米流体各个工况下的沸腾传热系数,其中热流密度、质量通量和传热系数的最大相对误差分别为 0.20%、0.50%和 0.61%。结果表明在 14~38 kW/m2下,纳米制冷剂沸腾传热系数随着热流密度的增加而增大,但当热流密度超过38 kW/m2时,传热系数反而下降了,分析认为在一定热流密度内,随着热流密度的增大,更多的壁面活化核心点被激活,通道壁面会产生更多的汽泡,有效强化了沸腾传热过程,传热系数明显增大;但当热流密度过高时,壁面上生成的汽泡过多且大量汽泡逐渐聚合形成气膜附着在加热壁面上,阻碍了壁面上液体的再润湿过程,不利于沸腾传热的进行,因此传热系数反而减小了。进一步研究发现纳米制冷剂的沸腾传热系数均比纯制冷剂高,其中质量分数0.10%的纳米制冷剂沸腾传热系数最高,可达4.25 kW/(m2·K),而纯制冷剂仅为2.42 kW/(m2·K),较纯制冷剂提高约76%,这说明向制冷剂中添加纳米颗粒配制成纳米流体可以提高传热性能,但并不是浓度越高传热效果越好,而是存在着最佳纳米颗粒浓度。 图6为在热流密度为38 kW/m2,系统压力为165 kPa,质量通量310.5 kg/(m2·s)试验工况下系统稳定运行后,通过采集一段时间内的试验段进出口压力数据,计算得到这段时间内的进出口压差数据,从而建立的单变量时间序列。不同浓度纳米流体流动沸腾时的压差波动并不是周期运动或者随机运动,具有一定的复杂性,另外不同浓度的纳米流体的压差平均值相比纯制冷剂,均有所降低,且浓度越高,平均值越低。 图5 纳米制冷剂与非纳米制冷剂传热系数Fig.5 Heat transfer coefficient of Al2O3/R141b and R141b 经计算得不同浓度纳米流体在微细通道内流动沸腾过程中压差时间序列的各个非线性特征量结果见表3,可以发现纯制冷剂和纳米流体的Hurst指数均大于0.5,这说明相应的流动沸腾系统在一定时间内具有较大的可预测性。根据文献[31],当Hurst指数大于0.5时,表明系统可能处于混沌状态,即纯制冷剂与纳米流体在微细通道内的流动沸腾均可能产生混沌状态。另外,纳米流体的 Hurst指数要大于纯制冷剂,其中 0.10 %的 Al2O3/R141b纳米流体的Hurst指数最高,达到0.72,说明浓度为0.10 %的Al2O3/R141b纳米流体最有可能达到混沌状态。 图6 不同浓度纳米制冷剂流动沸腾压差信号的单变量时间序列Fig.6 Time series of flow boiling pressure differential signals of nano-refrigerant with different mass fractions of nano-fiuids 表3 压差信号各非线性特征量计算结果Table 3 Calculation results of nonlinear eigenvalues of pressure differential signals 图 7为关联维数随嵌入维数的变化规律,可以看出不同浓度纳米流体流动沸腾系统的关联维数均随嵌入维数的增加逐渐趋于平稳,表明各个系统均处于混沌状态,纳米流体的关联维数高于纯制冷剂,说明纳米流体在微细通道内的流动沸腾系统更加复杂,其中质量分数为0.10%的纳米流体关联维数达到了5.20。 不同浓度纳米流体压差波动时间序列的最大 Lyapunov指数和Kolmogorov熵值均大于0,进一步证明了其流动沸腾系统均已进入混沌状态,其中质量分数为0.10 %时,最大Lyapunov指数值和K熵值分别为0.4830和0.67,均为最大值,故质量分数为0.10 %的纳米流体在微细通道内流动沸腾传热的混沌程度最强。 图7 不同浓度纳米流体流动沸腾系统关联维数与嵌入维数的关系Fig.7 Relationship between correlation dimensions and embedding dimensions of flow boiling system with different mass fractions of nano-fluids 根据以上的试验和计算结果可以发现微细通道内纳米流体流动沸腾系统的各非线性特征量与系统的传热系数存在一定的对应关系,不同浓度纳米流体的各项非线性特征量均比纯制冷剂大,其沸腾传热系数也比纯制冷剂大,系统混沌性更强,传热效果也更好。分析认为这是由于纳米颗粒的加入对微细通道内汽泡的形成、生长、脱离产生了影响,根据文献[32]的研究,纳米颗粒的加入主要作用于流体的相界面,可以使得微细通道内沸腾时产生的汽液固三相线向汽相一侧移动,导致汽泡脱离直径变小,脱离频率增大,通道内产生的小汽泡更多,其与通道内的液体工质摩擦作用增强,使得微细通道内流体的湍流强度增加,系统变得更加复杂,混沌性更强,各项非线性特征量增大。更多的小气泡会带走更多的热量,大量气泡的脱离也会对近壁面的温度边界层产生强烈的扰动作用,从而大幅提高传热效率,另外添加纳米颗粒也会使流体的导热性有所增强,传热效果进一步强化。但从计算结果中也发现当纳米流体质量分数超过0.10%,混沌程度和传热系数反而降低了,这是因为微尺度条件下纳米颗粒在壁面的沉积会在一定程度上增加传热壁面的传热热阻并且使壁面的润湿性增强,在低浓度纳米流体中,这种改变十分微小,但当纳米流体浓度超过一定限值时,其传热壁面热阻明显增大,壁面润湿性明显增强,工质汽化所需的壁面过热度明显升高[33-34],通道内产生的小气泡数量减少,反而使系统混沌作用有所减弱,传热效率降低。 本文通过对纳米流体与非纳米流体在2 mm×2 mm微细通道内流动沸腾系统的非线性特性进行定性和定量的分析。 1)本试验范围内,Al2O3/R141b纳米流体与纯制冷剂R141b在微细通道内的流动沸腾均处于混沌状态,其Hurst指数均大于0.5,关联维数、K熵、最大Lyapunov指数均为大于0的有限值。 2)纳米流体流动沸腾系统的各项非线性特征量相比纯制冷剂均有所增大,其流动沸腾传热系数相比纯制冷剂也有所提高,说明向纯制冷剂中添加纳米颗粒后,微细通道内流动沸腾系统变得更加复杂,混沌性更强,传热能力也得到提升。 3)微细通道内纳米流体流动沸腾系统的混沌程度随着浓度的升高先增强后减弱,其沸腾传热系数也随着浓度的升高先增加后减小,试验工况下质量分数为0.10%的纳米流体流动沸腾系统的各项非线性特征量达到最大值,相应的沸腾传热系数也为最大,其平均沸腾传热系数相比纯制冷剂提高了约76%。 [1] Yavatkar R, Tirumala M. Platform wide innovations to overcome thermal challenges[J]. Microelectronics Journal,2008, 39(7): 930-941. [2] 郑捷庆,何宏舟,袁嘉隆,等. 矩形微通道热沉内变物性工质的流动与换热特性[J]. 农业工程学报,2015,31(21):205-210.Zheng Jieqing, He Hongzhou, Yuan Jialong, et al. Flow and heat transfer characteristics in rectangular microchannel heat sinks using coolant with variable thermal property[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2015, 31(21): 205-210. (in Chinese with English abstract) [3] Karayiannis T G, Mahmoud M M. Flow boiling in microchannels: Fundamentals and applications[J]. Applied Thermal Engineering, 2017,115(25):1372-1397. [4] Yu L, Sur A, Liu D. Flow boiling heat transfer and two-Phase flow instability of nanofluids in a minichannel[J].Journal of Heat Transfer, 2015, 137(May): 51501-51502. [5] Wan Z, Deng J, Li B, et al. Thermal performance of a miniature loop heat pipe using water–copper nanofluid[J].Applied Thermal Engineering, 2015, 78: 712-719. [6] Li X, Cheung S C P, Tu J. Nucleate boiling of dilute nanofluids-mechanism exploring and modeling[J]. International Journal of Thermal Sciences, 2014, 84(4): 323-334. [7] Prajapati O S, Rohatgi N. Flow boiling heat transfer enhancement by using ZnO-water nanofluids[J]. Science &Technology of Nuclear Installations, 2014(4): 246-250. [8] Paruya S, Goswami N, Pushpavanam S, et al. Periodicallyforced density wave oscillations in boiling flow at low forcing frequencies: Nonlinear dynamics and control issues[J]. Chemical Engineering Science, 2016, 140(2): 123-133. [9] Zhou L, Li Y, Wei L, et al. Multi-jet flows and bubble emission during subcooled nucleate boiling of aqueous n-butanol solution on thin wire[J]. Experimental Thermal &Fluid Science, 2014, 58(10): 1-8. [10] Prasad G V D, Pandey M. Parametric effects on reactivity instabilities and nonlinear oscillations in a nuclear-coupled double channel natural circulation boiling system[J]. Nuclear Engineering & Design, 2010, 240(5): 1097-1110. [11] 强爱红,刘明言,孙永利. 汽液固三相流动沸腾传热系统的非线性特性[J]. 化工学报,2005,56(5):779-785.Qiang Aihong, Liu Mingyan, Sun Yongli. Nonlinear characteristics in vapor-liquid-solid flow boiling system[J]. Journal of Chemical Industry & Engineering, 2005, 56(5): 779-785.(in Chinese with English abstract) [12] Langford H M, Beasley D E, Chterbeck J M. Chaos analysis of pressure signals in upward air-water flows[C]// Third International Conference on Multiphase Flow, ICMF’98, France,1998. [13] Gavilán-Moreno C J, Espinosa-Paredes G. Using largest lyapunov exponent to confirm the intrinsic stability of boiling water reactors[J]. Nuclear Engineering & Technology, 2016,48(2): 434-447. [14] Jin D L, Pan C. The complex nonlinear dynamics in the multiple boiling channels coupling with multi-point reactors with constant total flow rate[J]. Annals of Nuclear Energy,2014, 71: 174-189. [15] 贾涛,王照亮,布文峰. 核态沸腾中汽化核心处温度时间序列的非线性分析[J]. 上海理工大学学报,2006,28(1):71-74.Jia Tao, Wang Zhaoliang, Bu Wenfeng. Nonlinear analysis of the temperature-time series at the nucleation site in nucleate boiling[J]. Journal of University of Shanghai for Science &Technology, 2006, 28(1): 71-74. (in Chinese with English abstract) [16] Tseng W J, Chen C N. Effect of polymeric dispersant on rheological behavior of nickel–terpineol suspensions[J].Materials Science & Engineering A, 2003, 347(1): 145-153. [17] Hwang Y, Lee J K. Production and dispersion stability of nanoparticles in nanofluids[J]. Powder Technology, 2008,186(2): 145-153. [18] Zhou J, Luo X, Deng C, et al. Influence of nanoparticle concentrations on flow boiling heat transfer coefficients of Al2O3/R141b in micro heat exchanger by direct metal laser sintering ☆ [J]. Chinese Journal of Chemical Engineering,2017,25(12):1714-1726. [19] Mahbubul M, Saidur R, Amalina M A, et al. Thermal conductivity viscosity and density of R-141b refrigerant based nanofluid[J]. Procedia Engineering, 2013, 56: 310-315. [20] Zhang C, Zhang L, Xu H. Investigation of flow boiling performance and the resulting surface deposition of graphene oxide nanofluid in microchannels[J]. Experimental Thermal and Fluid Science, 2017, 86: 1–10. [21] 罗小平,邓聪,冯振飞,等. 制冷系统不同表面能微通道的流动沸腾传热特性试验[J]. 农业工程学报,2016,32(20):217-222.Luo Xiaoping, Deng Cong, Feng Zhenfei, et al. Flowing boiling heat transfer characteristics test for microchannels with different surface energy in refrigeration system[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2016, 32(20): 217-222. (in Chinese with English abstract). [22] Lee H, Park I, Mudawar I, et al. Micro-channel evaporator for space applications – 1. Experimental pressure drop and heat transfer results for different orientations in earth gravity[J]. International Journal of Heat and Mass Transfer,2014, 77(4): 1213–1230. [23] Yin L, Jia L, Guan P, et al. Experimental investigation on bubble confinement and elongation in microchannel flow boiling[J]. Experimental Thermal & Fluid Science, 2014,54(2): 290-296. [24] Figueiredo A B, Baptista R M, Rachid F B D F, et al.Numerical simulation of stratified-pattern two-phase flow in gas pipelines using a two-fluid model[J]. International Journal of Multiphase Flow, 2017, 88: 30-49. [25] Drahos J, Bradka F, Puncochar M. Fractal behaviour of pressure fluctuations in a bubble column[J]. Chemical Engineering Science, 1992, 47(15): 4069-4075. [26] Carr J R. Statistical self-affinity, fractal dimension, and geologic interpretation[J]. Engineering Geology, 1997, 48(3):269-282. [27] Altunkaynak B, Kilic C, Klimek M D. Multidimensional phase space methods for mass measurements and decay topology determination[J]. European Physical Journal C,2017, 77(2):61. [28] Grassberger P, Procaccia I. Characterization of strange attractors[J]. Phys Rev Lett , 1983 , 50(5): 346-349. [29] Rosenstein M T, Collins J J, Luca C J D. A practical method for calculating largest Lyapunov exponents from small data sets[J].Physica D Nonlinear Phenomena, 1993, 65(1): 117-134. [30] Albano A M, Passamante A, Farrell M E. Using higher-order correlations to define an embedding window[J]. Physica D Nonlinear Phenomena, 1991, 54(1): 85-97. [31] Coeurjolly J F, Porcu E. Properties and Hurst exponent estimation of the circularly-symmetric fractional Brownian motion[J]. Statistics & Probability Letters, 2017, 128(4):21-27. [32] 徐立, 李玉秀, 徐进良, 等. 微通道中纳米流体流动沸腾换热性能研究[J]. 高校化学工程学报, 2011, 25(4): 559-564.Xu Li, Li Yuxiu, Xu Jinliang, et al. Flow boiling heat transfer performance of nanofluids in a microchannel[J]. Journal of Chemical Engineering of Chinese Universities, 2011, 25(4):559-564. (in Chinese with English abstract) [33] Hai T P, Caney N, Marty P, et al. Flow boiling of water in a minichannel: The effects of surface wettability on two-phase pressure drop[J]. Applied Thermal Engineering, 2011, 31(11):1894-1905. [34] Tang X, Zhao Y H, Diao Y H. Experimental investigation of the nucleate pool boiling heat transfer characteristics of δ-Al2O3-R141b nanofluids on a horizontal plate[J].Experimental Thermal & Fluid Science, 2014, 52: 88-96.
2.4 相空间重构及关联维

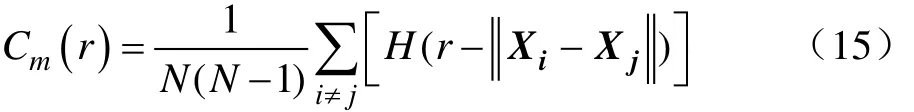


2.5 最大Lyapunov指数及Kolmogorov熵

3 结果与分析
3.1 纳米制冷剂流动沸腾试验结果




3.2 讨论
4 结 论

