双离合自动变速器预选挡特性分析及控制策略

刘 玺，何 仁，程秀生

0 引 言

预选挡是双离合自动变速器（dual clutch transmission，DCT）换挡过程的关键环节之一。由于DCT具有相邻挡位分属奇偶离合器的结构特点，当车辆以某一挡位行驶时，可控制另一离合器对应挡位的换挡拨叉进行预选挡，使目标挡位在换挡点到来之前及时就绪，到达换挡点后，通过控制两离合器交互，实现当前挡位向目标挡位过渡，完成换挡[1-5]。由此可见，预选挡是离合器交互的前提，要实现快速、舒适的换挡，预选挡控制必须及时、平稳[6]。

国内外学者对选挡特性进行了大量研究，并且取得了很多有价值的成果。Kunal等[7]对同步器进行建模并对换挡力进行了仿真；Lovas等[8]研究了同步器滞滑现象对换挡力的影响；Singh等[9]对拨叉刚度与换挡质量之间的关系进行了研究；马明月等[10]采用遗传算法对换挡元件进行了优化；Oh等[11]对DCT换挡过程进行了建模仿真；沈文臣等[12]通过建立换挡机构的动态耦合模型来换挡过程中的换挡力控制问题；这些研究大多旨在探明换挡机构参数对换挡力的影响，对换挡机构进行优化设计。在选挡过程控制方面，国内学者对自动变速器换挡过程的选挡执行机构控制方法及动力传动系统的扭矩变化进行了研究[13-16]，但由于DCT奇偶挡位分属不同离合器的结构特点使其具有特殊的预选挡过程[17]，上述成果并没有充分考虑并利用这一特殊性。本文从DCT换挡机构的结构出发，对预选挡过程进行运动学与动力学分析，研究各阶段选挡特性，制定基于DCT特性的预选挡策略。在此基础上，提出基于换挡拨叉位置闭环的换挡力控制策略，以期获得较好的预选挡品质，为实现DCT快速平稳的预选挡功能提供参考，也为手动变速器的换挡力分析提供了参考。

1 DCT预选挡特性分析

1.1 DCT预选挡原理及策略

DCT预选挡包括2个方面的内容：一是离合器切换前，实现目标挡位同步器的结合，即挂挡操作；另一方面是在离合器切换完成后，实现前一挡位同步器的分离，即摘挡操作。这 2个过程都会使与同步器主从动部分相连部件的转矩发生改变，因此有必要对预选挡过程中DCT的动力传递原理进行讨论。

DCT是在平行轴式变速器基础上发展而来，2个液压驱动的湿式离合器采用同心布置结构，各自连接一根输入轴，实心内轴和中空外轴上的齿轮分别与奇偶挡位的被动齿轮啮合。当车辆在某一挡位行驶时，相邻挡位的离合器完全分离，该挡所在离合器完全结合，将发动机转矩经挡位齿轮传递至驱动轮。这种结构使相邻挡位同步器的预先结合成为可能，到达换挡点后，进行 2个离合器切换，即可实现换挡[18-19]。从动力传递的角度可将DCT工作原理简化为图1所示。

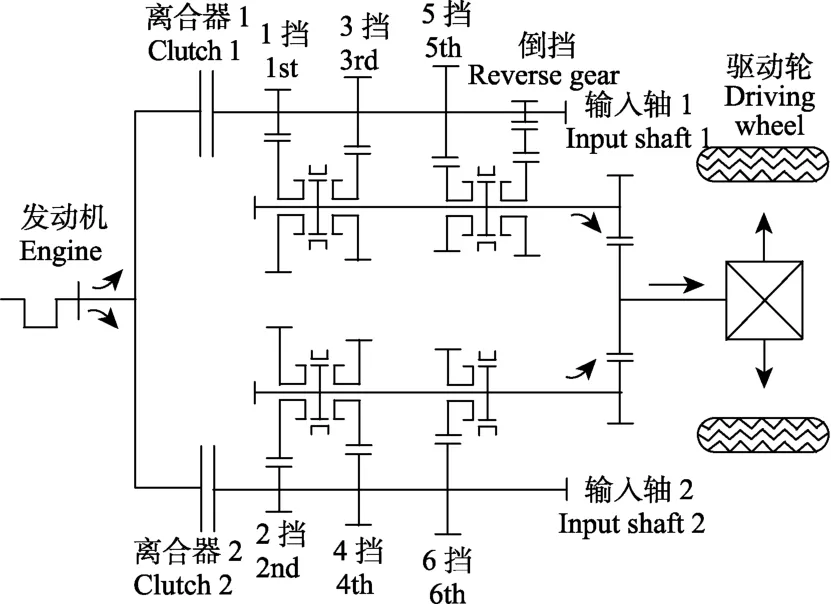
图1 DCT工作原理示意图Fig.1 Working principle diagram of DCT

手动或机械式自动变速器工作时，除当前挡位所在齿轴外，其它齿轴都处于自由转动状态，同步器结合前，无法对待结合齿圈相连轴齿进行调速，同步器结合套与待挂入挡位接合齿圈的转速差不可控，转速差较大时，会延长同步时间，带来同步器的过度磨损和烧蚀。但是DCT具有双离合器结构，当前挡位离合器处于结合状态，传递发动机全部扭矩；另一离合器处于自由可控状态，其从动部分连接待结合齿圈所在的齿轴。当该离合器无压力时，由于带排转矩的作用，离合器从动端以较低的转速转动[20-21]；当压力逐渐增大时，离合器从动端转速逐渐升高，处于滑摩状态；当压力足够大时，离合器主从动端转速差为0，处于结合状态。因此可以通过对该离合器的压力控制，实现待结合齿圈所在齿轴的调速，减小同步器主从端转速差，降低同步过程滑摩程度，缩短同步时间。

基于上述分析，可见DCT预选挡的独特性主要体现在挂挡过程。本文制定的挂挡策略具体如下：1）在接近换挡点时，计算待挂入挡位同步器主动端，即同步器结合套转速 n1；根据目标挡位离合器从动部分当前转速，计算待挂入挡位同步器从动端，即待接合齿圈转速 n2；假设目标挡位离合器结合，计算待挂入挡位同步器从动端转速n3；2）分析比较n1、n2和n3三者之间的关系，按照表 1所示的策略对目标挡位离合器进行控制，使同步器主从动端转差最小；3）同步器主从动端转差达到最小后，目标挡位离合器压力迅速降到最小，控制目标挡位拨叉操纵同步器，完成同步过程，实现挂挡。

表1 DCT预选挡目标挡位离合器控制策略Table 1 Control strategy of clutch for gear pre-selection

摘挡过程相对短暂，整个过程步器主从动部分转矩基本不变，具体摘挡策略为：离合器交互完成后，控制上一挡位拨叉将同步器结合套推回中间空挡位置，同步器主从端分离。

1.2 DCT预选挡特性

根据DCT预选挡机构的机械结构，可从运动学与动力学角度，分别对挂挡、摘挡特性进行分析。

1.2.1 挂挡特性分析

挂挡开始后，同步器结合套在拨叉作用下，克服结合套空挡自锁阻力，离开中间空挡位置做轴向运动，使同步器外锥环、中间环、内锥环及换挡齿轮摩擦锥面相互挤压，形成 3个摩擦副，在持续的摩擦力作用下，外锥环和结合套的转速迅速接近接合齿圈转速，实现结合套与外锥环的啮合，即同步锁止；随后结合套继续移动，结合套内花键齿端倒角与接合齿圈相应齿端倒角接触后，作用在接合齿圈花键齿端斜面上的切向分力就会使齿圈及与之相连的所有零件一起相对于结合套向前旋转一个角度，结合套和结合齿圈啮合，完成整个挂挡过程[22]。在此过程中，随着轴向位置的改变，结合套受到不同力的作用。

1）结合套空挡自锁阻力

结合套空挡自锁装置结构简图如图2a所示。当于中间空挡位时，定位钢球在弹簧压力下嵌入凹槽，阻止结合套轴向运动，防止自行挂挡。挂挡时，换挡拨叉轴向作用在结合套上，克服自锁弹簧的阻力将定位钢球从凹槽中挤出推回孔中，其动态受力分析如图2b所示。

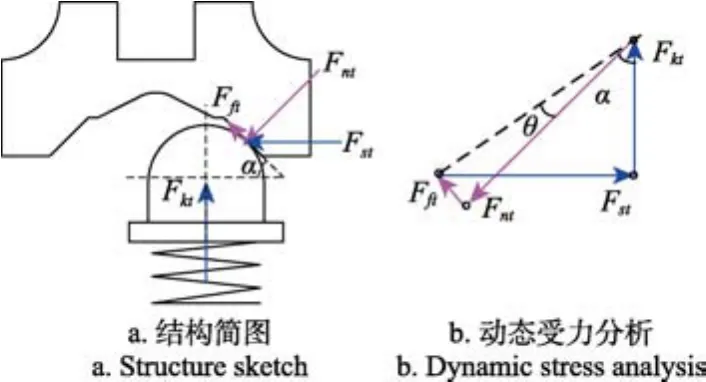
图2 结合套空挡自锁装置受力分析Fig.2 Force analysis of sleeve self-locking devices in neutral

设x为轴向方向，y为径向方向，则结合套空挡自锁装置受力分析如下

式中 Ft0为自锁弹簧预紧力，N； kt为自锁弹簧刚度，N/mm；Δy为自锁弹簧压缩量，mm。

钢球在凹槽内运动过程中，定位钢球与凹槽壁面间的摩擦力极小，即Fft≈0，故可取近似值θ=0，结合式（1）、（2）可得该过程中结合套空挡自锁阻力为

钢球被挤出凹槽推回孔中后，α=0，此时结合套在轴向只受到摩擦力Ftf，即

式中hs为凹槽深度，mm；μb为结合套与钢球间的摩擦系数。

2）同步力

结合套离开中间位置后，继续轴向移动，逐渐消除同步器各部件的间隙后，在同步力的作用下产生同步力矩，开始同步过程，该过程中同步器受力分析如图3所示。

图3 同步器受力分析Fig.3 Force analysis of synchronizer

分别对同步器主、从动部分进行动力学分析，可以得到同步过程中同步器主、从动部分的运动微分方程为

式中t为时间，s。

同步前，若ωf>ωrifir，则K=1，反之，K=–1。对于本文研究的三锥同步器，同步力矩与同步力的关系为

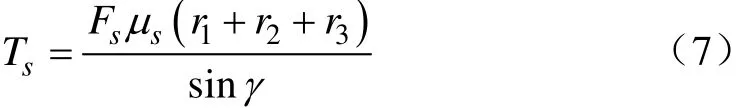
式中μs为同步器摩擦锥面间的摩擦因数；r1、r2、r3分别为3个摩擦锥面的摩擦半径；γ为摩擦锥面的半锥角。

假设在同步过程中，Tt、Te、Ts和 Tv为常数，对式（5）、（6）积分可得

式中A、B为积分待定常数。

同步过程的初始条件为

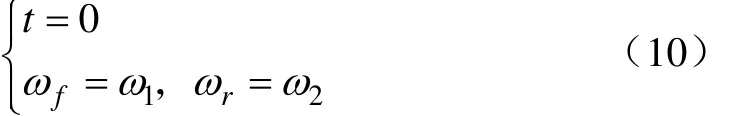
在同步力作用下，同步器主从动部分转速逐渐接近直至相等，同步结束条件为

式中 ω1为同步开始时目标挡位离合器从动部分转速，rad/s；ω2为同步开始时变速器输出轴转速，rad/s；ts为同步时长。

综合式（7）～（11），最终可以得到同步力与同步时长的关系表达式为

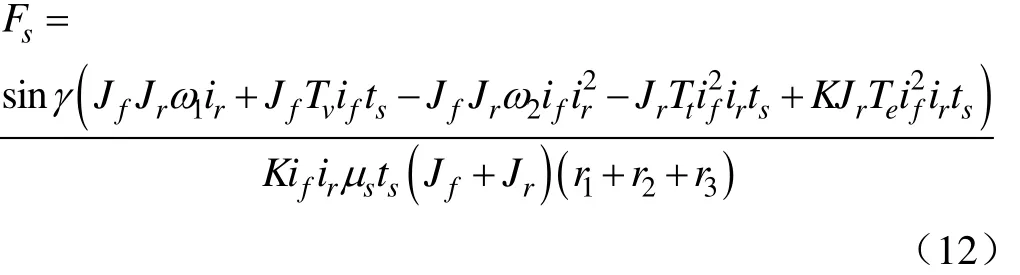
3）结合齿圈抵触阻力

同步器主从动部分转差消失后，结合套在换挡力的作用下与外锥环啮合，随后继续轴向移动直至与接合齿圈齿端相抵触，对齿圈齿端会产生切向分力，使结合齿圈及其相连的组件相对于外锥环发生转动，结合套和齿圈啮合，完成挂挡[23]。此过程受力分析如图4所示。

图4 结合齿圈抵触阻力分析Fig.4 Resistance analysis of connection gear ring

以结合套向齿圈运动的轴向方向为x轴正方向，齿圈相对结合套旋转的切线方向为y轴正方向，在齿圈及与之相连组件的惯性力矩作用下，结合套受到抵触阻力，由转动定律得

结合齿圈抵触阻力由结合套内齿对齿圈花键齿正压力及滑动摩擦力在轴向的两部分分量组成

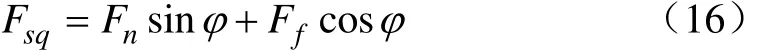
式中Jq为结合齿圈及相连组件转动惯量，kg·m2；dq为齿圈齿端平均半径，m；x为齿圈轴向位移，m；μq为结合套内齿与齿圈花键齿间的摩擦系数。

联立式（13）～（16），即可得到接合齿圈抵触阻力Fsq为

在结合套和齿圈啮合，完成挂挡同时，换挡拨叉自锁装置中的自锁弹簧将自锁钢球压入换挡拨叉的凹槽，使换挡拨叉轴向位置固定，防止自行脱挡。

1.2.2 摘挡特性分析

在选挡执行机构中，由液压系统提供的主压力，经过选挡力控制电磁阀调节后，作用在拨叉液压缸中的活塞上，推动活塞，进一步带动选挡拨叉，将自锁钢球从拨叉的凹槽中推出，进而带动结合套沿轴向运动至中间空挡位置，完成退挡。换挡拨叉自锁装置结构及受力分析如图5所示。

图5 换挡拨叉自锁装置受力分析Fig.5 Force analysis of shifting fork self-locking devices

结合图2与图5，可知换挡拨叉自锁装置与结合套空挡自锁装置的受力过程类似，参照结合套自锁阻力求解过程，设x为轴向方向，y为径向方向，摘挡过程中换挡拨叉自锁装置中定位钢球与拨叉凹槽壁面之间摩擦力极小，即Ffb≈0，故可取近似值δ=0，最终可得换挡拨叉自锁阻力为

式中Fb0为自锁弹簧预紧力，N；kb为自锁弹簧刚度，N/mm。

换挡拨叉将定位钢球挤出凹槽后，β=0，在轴向只受摩擦力Fbf作用，其表达式为

式中hb为拨叉凹槽深度，mm；μb为换挡拨叉与定位钢球间的摩擦系数。

综合上述分析，基于预选挡工作原理，结合预选挡过程运动学、动力学特性，按照拨叉的位移，可将挂挡过程顺序分为滑块滑动、同步、同步环拨正、穿过同步环、结合齿拨正、轴套与结合齿啮合 6个阶段，将摘挡过程分为解除换挡拨叉自锁和拨叉回位 2个阶段。各个阶段拨叉所受阻力如图 6所示。在换挡力作用下，换挡拨叉克服各阶段阻力，完成该阶段的轴向位移，最终实现预选挡。

图6 预选挡过程拨叉位置-阻力关系示意图Fig.6 Diagram of relationship between fork position and resistance in gear pre-selection

2 DCT预选挡过程的换挡力分析

2.1 DCT预选挡品质评价指标

从上节分析可知，预选挡过程中每个阶段换挡拨叉受力各不相同，换挡力决定了预选挡机构的工作状态，进而影响预选挡品质，因此有必要根据预选挡品质要求，对换挡力进行分析。

1）冲击度。预选挡过程会影响车辆纵向加速度的变化率，即冲击度。根据图3所示的同步过程动力学模型，该过程冲击度js可以表示为式中a为车辆纵向加速度，m/s2；rw为车轮滚动半径，m；iw为主减速比。

再结合式（7），最终可得同步过程中冲击度为

根据图 4所示的结合齿圈抵触阻力模型，结合式（17），同理可得结合套与接合齿圈啮合过程的冲击度为

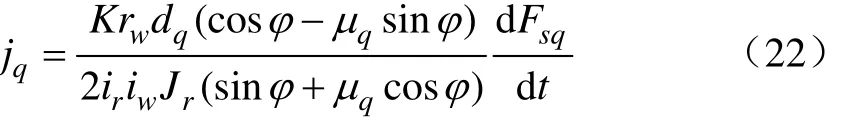
2）滑磨功率。滑磨功率是指同步力矩在同步器摩擦锥面上单位面积、单位时间所做的功，用来衡量同步器的滑磨程度[24]。取三锥同步器中的一对摩擦面为研究对象，则有

式中Ls为滑磨功率，W。

同步过程换挡力恒定，则摩擦面间的相对滑动速度呈线性变化，结合式（10）、式（11），可得同步过程中的任意时刻

将式（24）代入式（25），可得同步期间滑磨功率的表达式为

2.2 基于预选挡品质评价指标的换挡力

冲击发生在换挡力变化的时刻。同步过程、结合套与接合齿圈啮合过程换挡力保持不变[25]，所以只需要考虑同步初始阶段及啮合初始阶段冲击度对预选挡品质的影响。人体对冲击度存在耐受范围，冲击度过大会影响舒适性甚至造成损伤[26]。设定冲击度允许值[j]，结合式（21）、（22），可得同步初始阶段及啮合初始阶段的换挡力变换率为

滑磨发生在同步过程，理想的预选挡过程需要较大的换挡力来实现缩短预选挡时间，但过大的换挡力会导致滑磨功率过大，加剧同步环磨损甚至烧蚀[27]。解决方式是在滑摩功率允许的前提下，采用最大换挡力来实现同步。设定极限滑磨功率[L]，结合式（25）可得

3 DCT预选挡控制

3.1 DCT预选挡过程拨叉位置分析

由上文得出的换挡力-拨叉位置对应关系可知，明确拨叉目标位置是计算换挡力的前提，根据预选挡原理及特性，制定出的挂挡和摘挡过程换挡拨叉目标位置如图7所示。

图7 预选挡过程拨叉目标位置示意图Fig.7 Diagrammatic target position of fork in gear pre-selection

挂挡过程分为3个阶段：0～te1阶段结合套离开中间位置对同步环进行预紧；te1～te2阶段结合套停止轴向运动进行同步；te2～te3阶段结合套继续轴向运动与结合齿圈啮合，完成挂挡。预紧阶段和啮合阶段时长可根据经验数据选取，结合式（12）、（28）可求得同步阶段时长为

摘挡过程分为2个阶段：0～tr1阶段结合套与原挡位齿轮脱离，tr1～tr2阶段结合套轴向运动至中间位置。各阶段时长可根据经验数据选取[28]。

从工程角度出发，为了便于应用，除同步阶段外，设定其它阶段拨叉做匀速运动，确定 te1、te2、te3、tr1和tr2后，结合拨叉及同步器结构参数，即可确定预选挡过程中任一时刻的拨叉目标位置。

3.2 DCT预选挡过程拨叉位置闭环控制

基于上文制定的预选挡过程拨叉目标位置，以及阻力-拨叉位置关系，提出拨叉位置闭环控制策略。如图 8所示，在预选挡过程中，根据拨叉目标位置和实际位置计算位置偏差及偏差变化率，输入模糊控制器，经模糊规则产生换挡力调节量，与拨叉实际位置对应的阻力求和后，最终作为目标换挡力输出。

图8 预选挡过程拨叉位置闭环控制策略Fig.8 Position closed-loop control strategy in gear pre-selection

设定拨叉位置偏差物理论域为[–1,1]，偏差变化率物理论域为[–0.5,0.5]，输入量化因子为6；换挡力修正量物理论域为[–30,30]，输出量化因子为0.1；模糊语言集为{负大，负中，负小，零，正小，正中，正大}，隶属函数为三角形均匀分布函数，基于Mamdani推理原则[29]，采用重心法进行反模糊化最终可得换挡力控制模糊规则如图9所示。

图9 换挡力控制模糊规则曲面Fig.9 Fuzzy rules surface of shifting force control

4 实车试验与分析

为了验证双离合自动变速器预选挡特性分析及控制策略的有效性，在搭载 6DCT的试验样车上进行预选挡试验。除DCT自身传感器外，试验在良好平直路面上进行，由于 1挡同步器主从动部分转动惯量相差最大，挂挡最困难，因此挂挡试验选用2挡降1挡时挂1挡过程，摘挡试验选择1挡升2挡后摘1挡过程，试验过程中拨叉目标位移和阻力是根据整车及DCT系统参数计算的理论值；拨叉实际位移、变速器输入、输出轴转速来自于传感器；在此基础上结合变速器参数，可计算出换挡力、齿圈转速和结合套转速，相关参数如表 2所示。试验车辆除DCT自身传感器外，还加装了法国FGP公司生产的加速度传感器 FA101，用于测试冲击度。实车试验平台如图10所示。试验结果分别如图11、12所示。

表2 试验样车主要参数Table 2 Main parameters of test prototype

图10 DCT实车试验平台Fig.10 DCT vehicle experiment platform

图11 2挡降1挡时挂1挡试验结果Fig.11 Test results of shifting into first speed during 2-1 downshift

从图11可以看出，初始阶段利用1挡所在的离合器迅速把结合齿圈转速从780下拉到640 rad/min，随后到达换挡点开始挂挡，挂挡过程中拨叉实际位置对目标位置跟踪误差不超过4.67%，整个过程用时约0.24 s，实际换挡力与理论阻力的最大误差不超过 12.3 N，在同步阶段和啮合阶段均出现了冲击，但冲击度最大值没有超过2 m/s3，几乎不影响舒适性。

图12 1挡升2挡时摘1挡试验结果Fig.12 Test results of shifting out of first speed during 1-2 upshift

由图12可知，摘挡过程用时约0.11 s，最大换挡力出现在开始阶段，用于克服拨叉自锁阻力。0.07 s时结合套与齿圈完全分离，换挡力迅速降低，随后结合套与齿圈出现转速差，整个过程冲击较小。

为了验证预选挡策略的可靠性，在实车试验的基础上，在试验台架上进行了模拟负载耐久试验，实物如图13所示。试验参照QC/T 1056-2017[30]进行，在试验台上完成1.6×105km换挡耐久等效试验后停机拆检，同步器锥环未出现磨损超限或烧蚀。

图13 DCT耐久试验实物图Fig.13 Picture of DCT endurance test

以上试验结果表明预选挡过程中冲击度和滑磨功率均满足要求，预选挡品质符合预期，验证了本文提出的双离合自动变速器预选挡策略的可行性和有效性。

5 结 论

1）针对 DCT特有的双离合器结构，制定了能够发挥结构优势的预选挡目标挡位离合器控制策略，通过对目标挡位离合器的压力控制，能够实现待结合齿圈所在齿轴的调速，减小同步器主从动部分转速差。

2）从运动学与动力学角度，分别对挂挡、摘挡特性进行分析，结合预选挡品质评价指标，得到预选挡过程中拨叉目标位置及对应换的换挡力，为拨叉位置闭环预选挡控制策略提供参考。

3）实车试验表明，可在0.24、0.11 s内分别完成降挡和升挡的预选挡过程，期间实际换挡力与理论阻力的最大误差不超过 12.3 N，拨叉实际位置对目标位置跟踪误差不超过4.67%；耐久试验显示同步器锥环未出现磨损超限或烧蚀。综合表明预选挡过程迅速平稳，冲击度和滑磨功率符合预期目标。该研究可以为双离合自动变速器预选挡特性及控制研究提供参考。

[1] 刘永刚，秦大同，叶明. 双离合器自动变速器电控单元控制策略模块化设计[J]. 机械设计与研究，2012，28(5)：74－79.Liu Yonggang, Qin Datong, Ye Ming. Research on control strategy of electronic control unit for dual clutch transmissions based on modular approach[J]. Machine Design & Research,2012, 28(5): 74－79. (in Chinese with English abstract)

[2] Kulkarni M, Shim T, Zhang Y. Shift dynamics and control of dual-clutch transmissions[J]. Mechanism & Machine Theory,2007, 42(2): 168－182.

[3] 张炳力，王伦珍. 双离合自动变速器特殊工况下换挡规律的智能在线修正研究[J]. 汽车工程，2015，36(6)：686－690.Zhang Bingli, Wang Lunzhen. A Research on the online intelligent correction of shift schedule for dual-clutch transmissions under special working conditions[J]. Automotive Engineering,2015, 36(6): 686－690. (in Chinese with English abstract)

[4] 刘振军，郝宏伟，董小洪，等. 湿式双离合器自动变速器换挡控制与仿真分析[J]. 重庆大学学报，2011，34(1)：7－14.Liu Zhenjun, Hao Hongwei, Dong Xiaohong, et al. Shifting control and simulation of wet dual clutch transmission[J].Journal of Chongqing University, 2011, 34(1): 7－14. (in Chinese with English abstract)

[5] Goetz M, Levesley M C, Crolla D A. Dynamics and control of gearshifts on twin-clutch transmissions[J]. Journal of Automobile Engineering, 2005, 219(8): 951－963.

[6] 赵治国，杨云云，陈海军，等. 干式DCT预换挡过程分析及拨叉轴位置伺服控制[J]. 中国公路学报，2015，28(10)：120－128.Zhao Zhiguo, Yang Yunyun, Chen Haijun, et al. Pre-shift process analysis and position servo control of shifting fork shaft for dry dual clutch transmission[J]. China Journal of Highway and Transport, 2015, 28(10): 120－128. (in Chinese with English abstract)

[7] Kunal R, Adiga G, Gill S, et al. Simulation of gear shift force curve and shift rail ramp profile[C]//SAE Technical Paper,2010-01-0896, 2010.

[8] Lovas L, Play D, Marialigeti J, et al. Mechanical behavior simulation for synchromesh mechanism improvements[J].Proc IMechE Part D: J Automobile Engineering, 2006,220(7): 919－945.

[9] Singh J, Verma A, Kunal R, et al. Shifter fork stiffness correlation to gear shift quality[J]. SAE International Journal of Commercial Vehicles, 2013, 6(2): 498－509.

[10] 马明月，刘艳芳，徐向阳，等. 基于遗传算法的AT换挡元件方案优选[J]. 北京航空航天大学学报，2014，40(10)：1372－1377.Ma Mingyue, Liu Yanfang, Xu Xiangyang, et al. Selection of shifting element design based on genetic algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014,40(10): 1372－1377. (in Chinese with English abstract)

[11] Oh J J, Choi S B, Kim J. Driveline modeling and estimation of individual clutch torque during gear shifts for dual clutch transmission[J]. Mechatronics, 2014, 24(5): 449－463.

[12] 沈文臣，胡宇辉，余天啸，等. 气动换挡执行机构压力特性仿真与试验[J]. 农业机械学报，2016，47(2)：338－348.Shen Wenchen, Hu Yuhui, Yu Tianxiao, et al. Simulation and experiment of pressure characteristics for pneumatic shifting actuator[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(2): 338－348. (in Chinese with English abstract)

[13] 赵鑫鑫，杨珏，张静，等. 液力自动变速器换挡过程的反演优化控制[J]. 农业工程学报，2016，32(增刊1)：27－33.Zhao Xinxin, Yang Jue, Zhang Jing, et al. Optimizing gear shifting quality with backstepping control for automatic transmission[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016,32(Supp.1): 27－33. (in Chinese with English abstract)

[14] 黄斌，吴森，付翔，等. 电驱动机械式自动变速器换挡过程研究[J]. 汽车技术，2015 (7)：18－23.Huang Bin, Wu Sen, Fu Xiang, et al. Research on shifting process of electric-drive mechanical transmission[J]. Automobile Technology, 2015(7): 18－23. (in Chinese with English abstract)[15] Walker P D, Zhang N. Modelling of dual clutch transmission equipped powertrains for shift transient simulations[J].Mechanism and Machine Theory, 2013, 6(2): 498－509.

[16] Mashadi B, Mansourian S M, Kakaee A H, et al. Control of a twin clutch transmission for smooth gearshifts[J]. Mathematical and Computer Modelling of Dynamical Systems, 2015, 21(4):389－409.

[17] 严忆泉，宋健，李亮. 干式双离合自动变速器分段优化换挡策略研究[J]. 农业机械学报，2014，45 (5)：30－36.Yan Yiquan, Song Jian, Li Liang. Multi-section optimization shift control method of dry dual clutch transmission[J].Transactions of the Chinese Society for Agricultural Machinery,2014, 45(5): 30－36. (in Chinese with English abstract)

[18] Galvagno E, Velardocchia M A, Vigliani A. Dynamic and kinematic model of a dual clutch transmission[J]. Mechanism and Machine Theory, 2011, 46(6): 794－805.

[19] 刘玺，何仁，程秀生. 基于驾驶员类型识别的双离合自动变速器换挡规律研究[J]. 农业工程学报，2015，31(20)：68－73.Liu Xi, He Ren, Cheng Xiusheng. Shift schedule of dual clutch automatic transmission based on driver type identification[J].Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2015, 31(20): 68－73. (in Chinese with English abstract)

[20] Iqbal S, Al-Bender F, Pluymers B, et al. Model for predicting drag torque in open multi-disks wet clutches[J]. Journal of Fluids Engineering, 2014, 136(2): 021103.

[21] 金涵宇. 基于湿式离合器的商用车 AMT动力传动系统一体化控制技术研究[D]. 长春：吉林大学，2016.Jin Hanyu. Research on Powertrain System Integrated Control Technology of Commercial Vehicle AMT Based on Wet Clutch[D]. Changchun: Jilin University, 2016. (in Chinese with English abstract)

[22] 付超，王明成，赵雪松，等. 双离合变速器锁环式同步器设计开发[J]. 传动技术，2016，30(2)：11－16.Fu Chao, Wang Mingcheng, Zhao Xuesong, et al. Design and development of blocker ring synchronizer for dual clutch transmission[J]. Drive System Technique, 2016, 30(2): 11－16. (in Chinese with English abstract)

[23] 史文库，姚为民. 汽车构造[M]. 北京：人民交通出版社，2013.

[24] Singh M P, Singh P, Kumar K, et al. Development of test method to validate synchronizer ring design for torsional fluctuations in manual transmission[C]//SAE Technical Paper,2016-28-0012, 2016.

[25] 陈震，钟再敏，章桐. 基于ADAMS的同步器同步过程仿真分析[J]. 汽车工程，2011，33(4)：340－344.Chen Zhen, Zhong Zaimin, Zhang Tong. Simulation analysis on the synchronizing process of synchronizer based on ADAMS[J]. Automotive Engineering, 2011, 33(4): 340－344.(in Chinese with English abstract)

[26] Eager D, Pendrill A M, Reistad N. Beyond velocity and acceleration: jerk, snap and higher derivatives [J]. European Journal of Physics, 2016, 37(6): 1－11.

[27] Walker P D, Zhang N. Transmission of engine harmonics to synchronizer mechanisms in dual clutch transmissions [J].Journal of Vibration and Acoustics, 2014, 136(5): 1－8.

[28] 刘玺. 湿式双离合器自动变速器换档过程关键技术研究[D]. 长春：吉林大学，2011.Liu Xi. Study on Key Technologies During the Shifting Process of Wet Dual Cluth Transmission[D]. Changchun: Jilin University,2011. (in Chinese with English abstract)

[29] Jantzen J. Foundations of Fuzzy Control: A Practical Approach [M]. John Wiley & Sons, 2013.

[30] 中华人民共和国工业和信息化部. 汽车双离合器自动变速器总成技术要求和试验方法：QC/T 1056-2017[S]. 北京：科学技术文献出版社.