拖拉机定速巡航系统纵向加速度跟踪控制

王 卓 刘知祥,2 白晓平 高 雷

(1.中国科学院沈阳自动化研究所， 沈阳 110016； 2.东北大学信息科学与工程学院， 沈阳 110819)

0 引言

农机自动驾驶系统是现代化农业中的重要作业装备，对农业增产增收发挥着越来越重要的作用。国内外对农机自动驾驶的研究主要集中在农机智能导航的农机运动学模型、导航路径跟踪控制以及导航定位新算法等方面，对农机巡航控制的研究不多，实际应用的则更少，但对汽车的巡航控制系统研究较多，在动力学系统模型和速度控制算法上取得了较多的研究成果[1-7]。大型农场轻载作业(播种和喷药等)的拖拉机、多功能收获机等采用定速巡航系统，能大大降低驾驶员劳动强度，减少有害气体排放，节省油料，提高生产效率。

针对农机的速度控制，相关专家学者进行了相应的研究和设计。COEN等[8]采用基于模型预测控制方法开发了联合收获机的巡航控制系统，降低发动机的油耗及噪声，简化操作人员的任务。FOSTER等[9]采用PID控制设计自走式割晒机的速度控制器。KAYACAN 等[10]在设计自动驾驶拖拉机时，通过PID控制器控制拖拉机的纵向速度。韩科立等[11]设计了增量式PID控制算法对拖拉机进行定速巡航控制。苗中华等[12]建立采棉机的行走速度调节模型，设计了模糊PID控制器，采用模糊规则和推理方法对PID参数进行调节，实时调节行走速度。郭娜等[13]针对插秧机在田间的工作特点及行驶速度的要求，将变论域引入模糊PID控制设计中，提高了插秧机行走系统的自适应性。上述控制器的设计方法能较好地克服外界的干扰，然而，在这些控制器中很少考虑行走系统本身的非线性特性以及外界干扰对行走系统参数的影响。

目前针对拖拉机的行驶速度控制系统主要考虑外界干扰，基本上采用传统的PID控制，而实际行驶过程中，系统模型参数会发生变化，并且低速行驶时，容易激发系统的未建模特性[14]。因此，有必要对系统的鲁棒性进行研究。农机定速巡航系统是农机自动驾驶的重要组成部分，其研究与设计是基于系统仿真与试验。本文基于雷沃TA800型拖拉机实验平台，研究拖拉机纵向动力学模型，其3个输入控制变量和2个输出响应变量分别是：油门开度、制动压力、挡位和加速度、行驶速度。主要针对拖拉机定速巡航系统各工况工作点下参数的变化以及外界的干扰，设计速度控制系统，引入车辆的标准定速巡航控制结构[15]，上层控制系统主要根据拖拉机行驶车速输出期望加速度，下层控制系统对执行机构进行控制跟踪期望加速度。

本文主要考虑下层控制器的设计，首先建立下层控制对象的数学模型，结合模型特点以及外界对系统的干扰，设计下层控制对象控制器，以改善系统的鲁棒性及响应特性。

1 定速巡航动力学系统传递函数模型

下层控制对象的数学模型是对拖拉机加速度控制系统进行分析和研究的基础。由于纵向动力学系统具有非线性部件，例如发动机等，且该动力学模型较复杂，通过公式推导该系统的近似线性化传递函数比较困难。因此，本文在通过机理分析及结合试验数据获得拖拉机纵向动力学模型的基础上，根据其非线性特点，对其进行线性化，将线性化的纵向动力学模型作为拖拉机定速巡航动力学系统模型。采用系统辨识的方法对拖拉机定速巡航动力学系统进行辨识，获得拖拉机定速巡航下层控制对象的传递函数模型。拖拉机定速巡航动力学系统模型结构如图1所示，图中ac表示控制器输出信号，αdes表示期望节气门开度，α表示节气门执行器实际输出角度，Pdes表示期望的制动压力，P表示制动执行器实际输出压力，a表示输出的实际加速度。

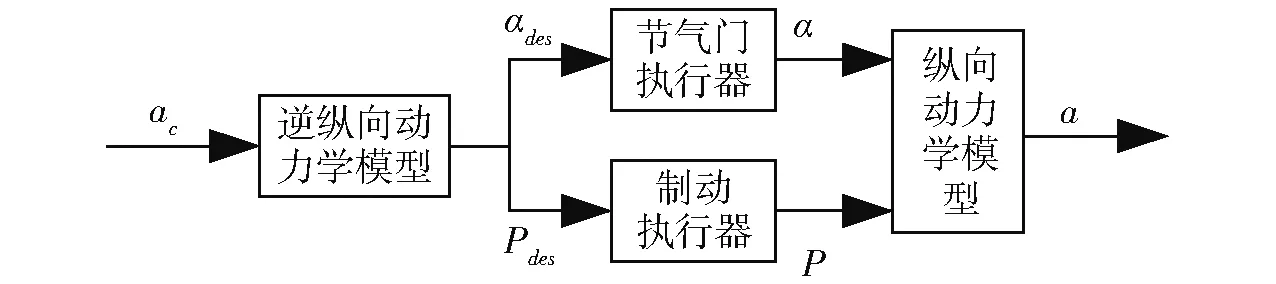
图1 拖拉机定速巡航动力学系统模型Fig.1 Dynamic system model of tractor cruise control

1.1 系统传递函数模型的辨识

对于线性系统的辨识方法，相关研究人员已经对其进行了深入的探讨和研究，总结出了一系列成熟的方法，依据是否要事先确定模型结构，可将它们分为两大类。一类叫做非参数模型辨识方法，不必事先确定过程模型的具体结构，采用响应曲线来描述，如时域的脉冲响应、阶跃响应及频率响应等，从而获得系统的数学模型；另一类是参数模型辨识方法，该方法事先确定一种模型结构，然后采用最小二乘法、最大似然辨识法、梯度法等方法来确定模型参数[16]。由于事先确定拖拉机定速巡航动力学系统传递函数模型结构较难，本文采用非参数模型辨识方法中经典的频率响应法，辨识线性化后的拖拉机纵向动力学系统。

根据频率响应辨识理论，向线性稳定系统输入正弦信号，则系统的频率响应信号与输入信号相同，其幅值和相位的变化为频率函数，且与系统的模型相关，因此可以运用频率响应试验确定稳定系统的传递函数模型[17]。根据上述原理，当拖拉机定速行驶在5、15、25 km/h工作点处和道路坡度角分别为0°、5°、10°的工况下，且挡位保持在常用工作挡位上，首先让系统处于非饱和状态，然后输入非死区的正弦信号幅值，然后在一定频率范围内，通过Simulink模块中的正弦信号发生器输入不同频率的正弦信号，作为拖拉机定速巡航动力学系统的期望加速度信号，改变输入正弦信号的频率，记录系统各频率点处输出信号的波形，该输出波形就是系统的加速度输出信号。频率响应试验原理图如图2所示。

图2 频率响应试验原理Fig.2 Frequency response experiment principle

由稳态段的输入输出信号的幅值比和相位差绘制对数频率特性曲线。图3是下层控制对象在各工作点处所对应的各工况下的对数幅频曲线。

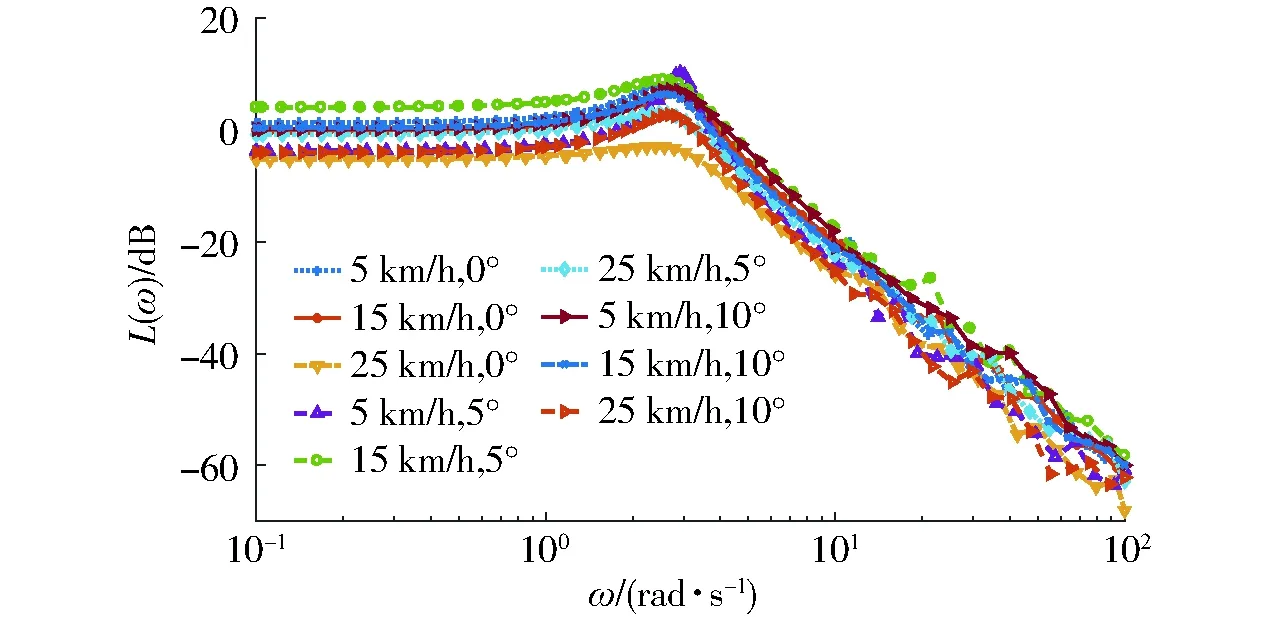
图3 系统对数幅频特性曲线Fig.3 Curves of log magnitude-frequency characteristics

分析所测数据，可知拖拉机运行在相同工况下和不同工作点上以及不同工况下和相同工作点上时，频率特性曲线都不相同，尤其是高频段幅值偏差较明显，所以拖拉机的动力学系统传递函数会随着工况的变化而改变。利用最小二乘法将多条频率响应特性曲线拟合成一条曲线，依据该曲线，按最小相位系统处理，推导出传递函数的模型结构并计算出模型各参数，忽略系统的延迟环节，作为下层控制对象的标称传递函数。

(1)

式中u——输入的加速度控制信号

图4是简化了的传递函数和实车加速度响应的比较，传递函数的加速度响应能很好地反映定速巡航动力学系统的仿真结果，因此，该标称传递函数可以用于下层控制器的设计。

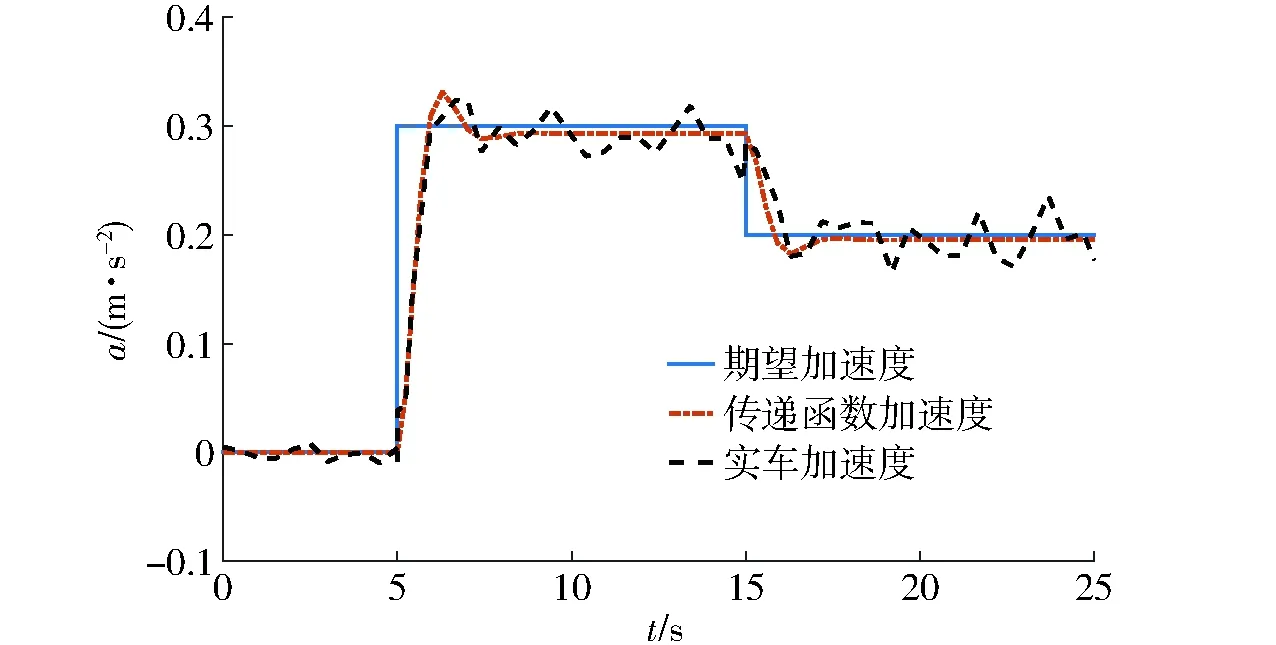
图4 传递函数模型加速度响应与实车加速度响应曲线Fig.4 Curves of acceleration response of transfer function model and real vehicle

1.2 下层控制系统工作原理

图5 标准定速巡航控制结构Fig.5 Structure of cruise control system

引入的标准定速巡航控制结构如图5所示，上层控制器根据驾驶员设定的行驶速度使拖拉机按设定速度行驶，并依据当前的行驶情况确定期望的加速度作为下层控制器的输入，下层控制器对拖拉机的定速巡航动力学系统进行控制，从而跟踪期望的加速度。由于上层控制器的设计相对较简单，采用PID控制即可满足需求，并以下层控制器的性能为基础，设计难点主要是下层控制器的设计，因此，本文主要考虑下层控制器的设计。

由于拖拉机的行驶速度相对较低，调节油门踏板的行程足可达到对系统的控制，所以本文主要考虑节气门的调节，制动踏板的控制主要用于系统停车以及行车安全。通过拖拉机试验，当加速度变化超过一定值时，例如陡长的下坡导致加速度变化过大，仅靠节气门调节需要较长的调节时间，因此会切换到制动系统，以减小加速度的过大变化，保证行车安全。

拖拉机定速巡航下层控制系统原理框图如图6所示，包括下层控制器、拖拉机逆纵向动力学模型、节气门执行器、拖拉机纵向动力学模型以及拖拉机传感系统。上层控制器输出的期望加速度ades作为下层控制器的输入信号，拖拉机逆纵向动力学模型根据输入的控制变量和拖拉机的行驶速度输出期望节气门角度，节气门执行器输出实际的节气门角度，拖拉机纵向动力学模型根据节气门角度计算出发动机输出转矩，从而跟踪期望加速度。

图6 下层控制系统原理框图Fig.6 Principle diagram of lower control system

2 滑模变结构控制器设计

滑模变结构控制是一种提高系统鲁棒性的有效方法，特别是在运动控制系统中的应用[18-19]，例如，CHOI等[20]设计了基于滑模控制的车辆纵向控制自适应观测器，WON等[21]在PATH项目中对前后车辆之间的距离控制采用了滑模控制算法，德国斯图加特大学的AXEL等[22]采用精确线性化方法及结合滑模控制方法来提高车辆加速度控制系统的鲁棒性。为了准确跟踪控制拖拉机的加速度响应、减小系统非线性特性的影响以及提高系统对模型参数变化和外界干扰的鲁棒性，本文设计了一个滑模变结构控制器作为下层控制器。

2.1 控制原理

滑模变结构控制可以迫使系统在一定特性下沿规定状态轨迹作小幅度、高频率的上下运动，如图7所示，在切换面s=0上运动点有3种：

(1)通常点(A)：系统运动点穿过切换面S时的点。

(2)起始点(B)：系统运动点到达切换面S附近时向切换面两侧离开时的点。

(3)终止点(C)：系统运动点到达切换面S附近时从切换面两侧趋近的点。

这3种情况，所有运动点都是终止点的区域为滑模区，系统在滑模区的运动称为滑模运动，在滑模区的运动都必须是C点的运动，当系统运动点运动到滑模区附近时需满足

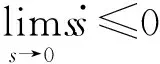
(2)

式中s——切换面函数

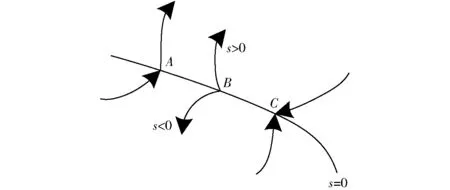
图7 切换面上3种点的特性Fig.7 Characteristics of three points on switching surface

滑模运动的模态轨迹是可以设计的，且与系统的参数及扰动无关。从而使得处于滑模运动的系统具有很好的鲁棒性[23]。由于拖拉机悬挂较大质量的农机具、道路坡度等引起系统参数发生变化并且低速行驶时容易引起的未建模特性，使用PID控制来设计控制器，不能提供足够的加速度响应控制性能。因此，设计滑模控制器来克服PID控制方法的不足。

2.2 控制器设计

对式(1)进行拉普拉斯反变换得到系统的微分方程为

(3)

式中t——时间

由于被控对象的传递函数是二阶的，且无零点，因此为消除较大的外界干扰对系统造成的稳态误差，设计带有积分项的加速度跟踪误差函数为

(4)

其中

e(t)=ades-a

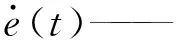
对式(4)进行求导，并结合式(3)求得

(5)

定义Lyapunov函数为

(6)

从而有

(7)

采用等速趋近律

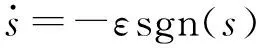
(8)

式中ε——系统运动点趋近切换面的速率 sgn(s)——符号函数

为降低滑动模态控制的抖振，将sgn(s)替换为饱和函数sat(s)

(9)

式中Δ——边界层

(10)

3 仿真与实验验证

3.1 基于Matlab的纵向动力学模型实现

利用Simulink建立各模块数学模型，并按照各模块间力矩的传递方式进行连接，所用参数是由实验平台雷沃欧豹TA800型拖拉机厂家提供以及实验测量的数据。拖拉机纵向动力学模型如图8所示，该系统的输入有4个：油门开度、挡位、制动压力以及行驶路面坡度，系统的输出量为行驶速度及加速度。

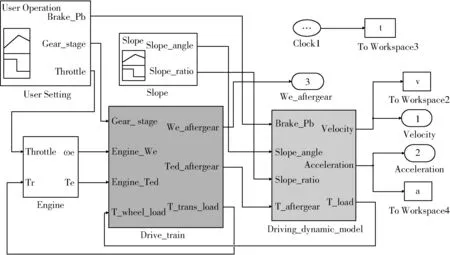
图8 拖拉机纵向动力学模型仿真框图Fig.8 Simulink simulation diagram of tractor longitudinal dynamics model

3.2 纵向动力学模型的验证及结果分析

为验证所建拖拉机纵向动力学模型的准确性和合理性，设计了拖拉机在水泥路面上行驶的典型工况实验，如表1所示。将实车实验所采集的数据和仿真结果进行对比，验证其稳态特性和动态特性的吻合程度。

表1 拖拉机纵向动力学模型验证实验工况Tab.1 Tractor longitudinal dynamic model validation test condition

实验平台如图9所示。将作用于所建模型的仿真输入信号通过设定的控制器的输入信号函数来实现，将控制器输出电信号作用于所设计的油门踏板调节机构的驱动器以及刹车行程的电动推杆，执行机构调节实际拖拉机平台上的油门踏板及刹车踏板，减少人为操纵的不确定性及不合理误差，挡位放置于常用的工作挡位上。仿真结果与实车实验结果如图10所示，其中速度的测量通过雷达地速传感器测量，加速度由农机自动导航系统中的GPS定位系统获得。

图9 拖拉机速度控制实验平台Fig.9 Experiment platform of tractor speed control

由仿真结果和实车实验结果对比可知，拖拉机纵向动力学模型能够很好地反映实车地纵向动力学特性。在3种典型工况下，仿真模型的速度和加速度响应的稳定误差不超过5%，其动态响应趋势与实车的响应结果具有较高的一致性。

3.3 控制算法仿真结果及分析

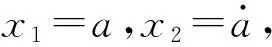
(11)

式中 d(t)——外界干扰项

在Simulink中的仿真框图如图11所示。

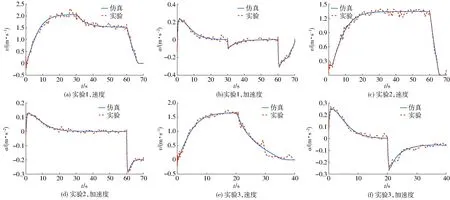
图10 仿真结果和实车实验结果对比Fig.10 Comparisons of simulation and experimental results

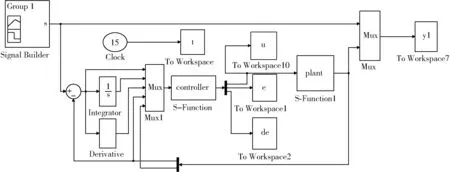
图11 控制器参数调节仿真框图Fig.11 Controller parameter adjustment simulation block diagram

将滑模变结构控制器与PID控制器进行比较。在工程实际中，PID控制应用广泛，其标称传递函数为

(12)

式中uo(t)——控制器输出信号KP——比例系数KI——积分系数KD——微分系数

针对标称传递函数，首先确定比例环节系数，令积分和微分环节系数为零，增大KP使输出信号振荡，然后再减小KP，找到临界振荡点，之后增大KI使输出信号达到目标值，最后针对超调和振荡情况适当增加KD，所调试的PID控制器参数：KP=4.5,KI=9.4,KD=0.8。根据期望的极点配置区域，即期望的最大最小阻尼系数，选择滑模控制器参数：c1=15,c2=0.815,Δ=45,ε=210。对所设计的控制器，在如下典型工况下进行仿真：t=0 s时，初始速度v0=0.5 m/s，初始加速度a0=0 m/s2，加速度变化幅值Δa=0 m/s2；t=3 s时，a0=0 m/s2，Δa=0.15 m/s2；t=7 s时，a0=0.15 m/s2，Δa=0.2 m/s2；t=11 s时，a0=0.15 m/s2，Δa=-0.1 m/s2。为检验控制系统的鲁棒性，加入坡度和拖拉机悬挂喷药系统产生质量变化的干扰，在7～11 s间，将道路坡度设定为5°，11～15 s间，坡度设定为-5°。

当加入坡度干扰以及拖拉机整体质量变化时，仿真结果如图12、13所示。

图12 加速度跟踪曲线Fig.12 Acceleration tracking curves

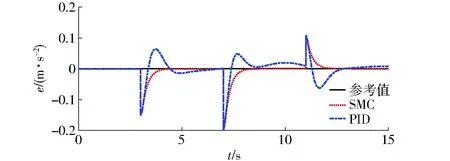
图13 加速度跟踪误差曲线Fig.13 Acceleration tracking error curves

图12、13是PID控制和滑模变结构控制(SMC)，在外加坡度干扰及整车质量发生变化时的加速度跟踪曲线以及加速度跟踪误差曲线。在0～7 s时间段内，增加500 kg的质量，未加入坡度干扰，由图12可知SMC控制器有更快的响应速度，且无超调，最大的稳态跟踪误差接近0，而PID在稳态阶段最大偏差为0.016 m/s2。7～15 s时间段内，在质量变化的干扰下叠加坡度干扰，并且伴有更大的加速度幅值变化以及减少加速度幅值，SMC控制器的跟踪误差的标准方差为0.046，而PID为0.076，可以得出外界干扰下SMC跟踪性能更稳定，并且跟踪速度更快，跟踪误差更小。

与PID控制器相比，SMC控制器对拖拉机加速度的控制，在响应速度、偏差精度及鲁棒性方面得到改善。此外，由仿真结果可知，相对于增加系统质量，坡度对系统的干扰要更大一些，而SMC控制器对路面坡度的干扰表现出良好的鲁棒性。

4 结论

(1)采用混合建模技术，对拖拉机的纵向动力传动系统进行机理分析，通过简化假设，并结合拖拉机实车数据，建立了拖拉机简化的纵向动力学模型。将所建模型在各典型工况下进行仿真，并将所获得的仿真数据与实车实验数据进行了对比，可以得出：所建模型能够准确地反映拖拉机行驶的纵向动力学特性，很好地兼顾了模型的准确性和简洁性，实现了整车全工况仿真，满足了拖拉机定速巡航系统对纵向动力学模型的要求。针对拖拉机定速巡航行驶工况下的加速度非线性特性，采用逆模型线性化方法对系统进行线性化，在线性化后的模型基础上，通过频率响应实验及最小二乘法获得系统的标称传递函数。

(2)由于系统的非线性及外界干扰对加速度响应的影响，设计了滑模变结构控制器来克服道路坡度以及增加系统质量负荷等对加速度跟踪控制的干扰。和PID控制相比，在坡度变化和由于悬挂农机具导致系统本身质量变化等的外界干扰情况下，该控制器有更好的跟踪响应速度和精度，对系统的参数变化及非线性干扰具有很好的鲁棒性。

1 胡静涛, 高雷, 白晓平, 等. 农业机械自动导航技术研究进展[J]. 农业工程学报, 2015, 31(10):1-10. HU Jingtao, GAO Lei, BAI Xiaoping, et al. Review of research on automatic guidance of agricultural vechicles[J]. Transactions of the CSAE, 2015, 31(10): 1-10. (in Chinese)

2 陈虹，宫洵，胡云峰，等．汽车控制的研究现状与展望[J]．自动化学报，2013，39(4)：322-346． CHEN Hong, GONG Xun, HU Yunfeng, et al. Automotive control: the state of the art and perspective[J]. Acta Automatica Sinica, 2013, 39(4): 322-346. (in Chinese)

3 RIGELSFORD J. Automotive control systems: for engine, driveline and vehicle[J]. Sensor Review, 2004, 11(4): 18-28.

4 GAO F, LI K, WANG J, et al. Adaptive throttle controller design based on a nonlinear vehicle model[C]∥American Control Conference, 2004 Proceedings of the IEEE, 2004:786-791.

5 韩科立, 朱忠祥, 毛恩荣,等. 基于最优控制的导航拖拉机速度与航向联合控制方法[J/OL]. 农业机械学报, 2013,44(2):165-170. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20130231&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2010.02.031. HAN Keli, ZHU Zhongxiang, MAO Enrong, et al. Joint control method of speed and heading of navigation tractor based on optimal control[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2013,44(2):165-170. (in Chinese)

6 KAYACAN E, RAMON H. Towards agrobots: identification of the yaw dynamics and trajectory tracking of an autonomous tractor[J]. Computers & Electronics in Agriculture, 2015, 115:78-87.

7 宋正河, 吕安涛, 陈文良, 等. 拖拉机自动驾驶系统的研究[J]. 拖拉机与农用运输车, 2005(5):1-5. SONG Zhenghe, LÜ Antao, CHEN Wenliang, et al. Research on tractor autonomous driving system[J]. Tractor and Farm Transporter,2005(5): 1-5. (in Chinese)

8 COEN T, SAEYS W, MISSOTTEN B, et al. Cruise control on a combine harvester using model-based predictive control[J]. Biosystems Engineering, 2008,99(1):47-55.

9 FOSTER C A, STROSSER R P, PETERS J, et al. Automatic velocity control of a self-propelled windrower[J]. Computers & Electronics in Agriculture, 2005, 47(1):41-58.

10 KAYACAN E, RAMON H, RAMON H, et al. Towards agrobots: trajectory control of an autonomous tractor using type-2 fuzzy logic controllers[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(1):287-298.

11 韩科立, 朱忠祥, 毛恩荣,等. 基于自动机械式变速的拖拉机定速巡航系统[J]. 农业工程学报, 2012, 28(4):21-26. HAN Keli, ZHU Zhongxiang, MAO Enrong, et al. Cruise control system of tractor based on automated mechanical transmission[J].Transactions of the CSAE, 2012, 28(4): 21-26. (in Chinese)

12 苗中华, 李闯, 韩科立,等. 基于模糊PID的采棉机作业速度最优控制算法与试验[J/OL]. 农业机械学报, 2015, 46(4):9-14,27. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150402&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2015.04.002. MIAO Zhonghua, LI Chuang, HAN Keli, et al. Optimal control algorithm and experiment of working speed of cotton-picking machine based on fuzzy PID[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2015,46(4):9-14,27. (in Chinese)

13 郭娜, 胡静涛. 插秧机行驶速度变论域自适应模糊PID控制[J/OL]. 农业机械学报, 2013, 44(12):245-251. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20131241&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2013.12.041. GUO Na, HU Jingtao.Variable universe adaptive fuzzy PID control of traveling speed for rice transplanter[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2013,44(12):245-251. (in Chinese)

14 GAO F, LI K, WANG J, et al. Adaptive throttle controller design based on a nonlinear vehicle model[C]∥American Control Conference, Proceedings of the IEEE, 2004:786-791.

15 RAJAMANI R. Vehicle dynamics and control[M]. Springer Science, 2006.

16 庞中华, 崔红. 系统辨识与自适应控制MATLAB仿真.[M]. 2版. 北京：北京航空航天大学出版社, 2013:11-15.

17 胡寿松. 自动控制原理[M]. 5版. 北京：科学出版社, 2007：187-206.

18 刘金琨. 滑模变结构控制MATLAB仿真:基本理论与设计方法[M]. 北京：清华大学出版社, 2015:1-17.

19 王海龙, 王刚, 陈曦,等. 仿海蟹机器人浮游步态动力学建模与运动控制[J]. 机器人, 2015，37(2):176-187. WANG Hailong, WANG Gang, CHEN Xi, et al. Dynamic modeling and motion control of a crablike robot in floating gait[J]. Robot, 2015, 37(2): 176-187.(in Chinese)

20 CHOI S B, HEDRICK J K. Vehicle longitudinal control using an adaptive observer for automated highway systems[C]∥American Control Conference, Proceedings of the IEEE, 1995:3106-3110.

21 WON M, KIM S S, KANG B B, et al. Test bed for vehicle longitudinal control using chassis dynamometer and virtual reality: an application to adaptive cruise control[J]. Journal of Mechanical Science and Technology, 2001, 15(9):1248-1256.

22 AXEL F, WERNER S. Nonlinear ACC in simulation and measurement[J]. Vehicle System Dynamics, 2001, 36(2-3):159-177.

23 UTKIN V. Variable structure systems with sliding modes[J]. IEEE Transactions on Automatic Control, 2003, 22(2):212-222.