舰空导弹舰上使用阶段战备完好性评估建模与分析

赵建印，王 玺，刘 星

（海军航空大学，山东烟台264001）

舰空导弹是现代海上防御作战中重要的舰载防空武器。舰空导弹战备完好性是影响其作战效能发挥的重要因素之一[1]。通过战备完好性模型的建立，可以定量地分析各影响要素与战备完好性的关系，为制定舰空导弹舰上使用保障方案和优化保障资源配置提供重要的理论依据。目前，关于装备战备完好性模型的研究多数停留在对装备的稳态使用可用度的评估以及基于装备时间的统计分析模型[2]，而面向具体装备和任务的战备完好性评估模型研究成果较少，且多以仿真模型[3-5]为主，很难实现针对具体任务和战备完好性要求制定和优化装备使用期间的保障方案[6-8]。

本文从舰空导弹舰上使用剖面出发，建立了给定舰上使用保障方案情况下舰空导弹瞬态战备完好性模型。

1 舰空导弹舰上使用剖面

舰空导弹舰上使用剖面是指舰空导弹从上舰到射击任务开始这段时间内所经历的全部事件和环境的时序描述[9-10]。

图1给出了舰空导弹舰上使用剖面的一般形式。舰空导弹装舰后长期处于战斗值班状态，当某一（随机）时刻来袭目标出现时，需要有足够数量的导弹处于可用状态，即战备完好状态。经过长期的舰上值班，舰空导弹能不能保持高的战备完好性，直接关系到防空作战的成败。

图1 舰空导弹舰上使用剖面Fig.1 Aviation missile ship used profile

2 舰空导弹舰上使用阶段战备完好性定义

武器装备的战备完好性是指当要求武器装备或武器系统投入作战时，该系统能够执行任务的能力或程度。战备完好性参数因装备的类型、任务范围和使用特点而异[4]。本文以发射准备好的概率为舰空导弹舰上使用阶段战备完好性参数。发射准备好的概率是指当来袭目标出现时每座发射装置均有足够数量的导弹处于可用状态的概率。这是一种面向任务的战备完好性定义。当来袭目标类型和数量不同时，要求可用导弹的数量也将有所不同，即任务不同，准备好的标准也不同[11]。

3 舰上使用阶段战备完好性模型

假设每座发射装置最大载弹量为m枚，在值班期间每枚导弹的故障过程是相互独立的[12]。

根据导弹舰上使用剖面，每座发射装置发射准备好的概率为：

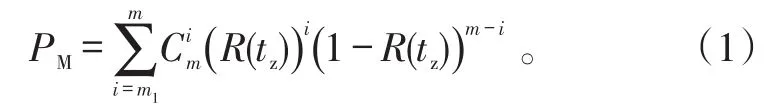
式（1）中：m1为处于发射准备好状态所要求的最少可用导弹枚数；m为每座发射装置最大载弹量；R(tz)为单枚导弹在值班tz时间内不发生故障的概率，即值班时间的可靠度。

当每枚导弹值班寿命均服从故障率为λz的指数分布时，式（1）可写为：

当值班时间tz服从某一概率密度函数为f(t)的随机分布时，R(tz)可由下式求得：

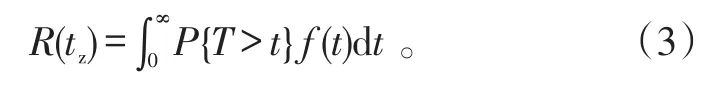
当导弹寿命服从参数为λz的指数分布，值班时间服从参数为 (μ,σ2)的正态分布时，式（3）可写成：

代入式（1）中，可得某一随机时刻舰空导弹战备完好性水平。

4 舰上使用阶段战备完好性的关联性分析

由式（1）可知，战备完好性与导弹值班可靠度有密切关系[13-15]。图2给出了在3种值班可靠度（值班4年）水平下PM随值班时间tz（1～12个月）变化曲线。

由图2可知，在相同值班时间条件下，值班可靠度越高，PM也越高；随着时间的增加，导弹出现故障的可能性越高，PM越低。PM是值班时间tz的递减函数。当值班时间较长时，导弹值班可靠度很可能无法满足较高的PM要求。在这种情况下，可以考虑在值班期间增加定期检测（定检）环节，若检测出故障，则立即更换舰上贮存的正常备用导弹，否则继续使用。

若给定PM的最低可接受值Pac，由式（1），可通过作图法找出在给定值班可靠度条件下允许的最长值班时间，然后根据导弹舰上使用保障相关规定确定定检时间。图3为值班4年可靠度为0.85时PM随值班时间变动曲线。假设Pac取0.95，则允许的最长值班时间为6个月，定检时间tc应不超过6个月。

图3 定检时间的确定Fig.3 Determination of verification time

给定定检时间tc和值班时间tz，则检测次数应满足：

当备用导弹数量充足时，nc等于tztc的整数部分。通过定检可以及时发现故障导弹并更换正常备用导弹，使每座发射装置导弹战备完好性恢复到较高水平。当备用导弹数量充足时，在定检时间PM被完全恢复如初，如图4所示。

图4 备用导弹充足情况下定检对PM的影响示意图Fig.4 PMdiagrammatic sketch of verification in the adequacy probability of standby missiles

接下来，进一步讨论定检时间给定的情况下如何确定舰上贮存备用导弹的数量。假设舰上贮存备用导弹的故障率远远低于值班导弹的故障率。在备用导弹数量充足的情况下，每个定检间隔期tc内，导弹故障过程可视为到达率为mλz的泊松过程，见图5。

图5 备用导弹充足情况下导弹故障和更换过程Fig.5 Missile failure and replacement process in the case of backup missile adequacy

在n个检测间隔期ntc内，共有i枚导弹发生故障的概率为：

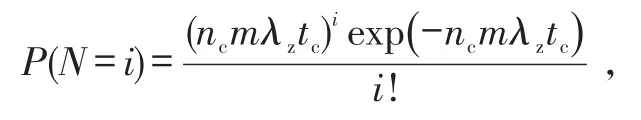
则备用导弹数量为s枚时，备用导弹充足概率为：

由式（5）可知，备用导弹充足概率主要与值班故障率、定检次数和定检时间有关。

图6给出了值班时间10个月、定检时间4个月时，备用导弹充足概率Ps与备用导弹s数量之间的关系曲线。在该定检时间下，要满足较高的备用导弹充足要求，每座发射装置备用导弹数量应以2～3枚为宜。

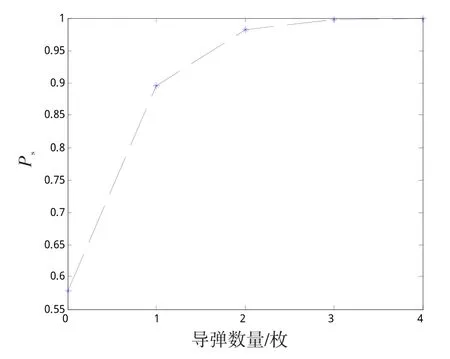
图6 备用导弹充足概率与备用导弹数量之间的关系Fig.6 Relationship between the adequacy probability of standby missiles and the number of standby missiles

5 有定检和备用导弹情况下战备完好性模型

式（1）给出了无定检情况下舰空导弹舰上使用阶段战备完好性模型。

在上述分析的基础上，下面讨论有定检和备用导弹的情况。

发射准备好主要包括2种情况[16-18]：

情况1：nc次定检期间备用导弹数量充足。该种情况下每座发射装置发射准备好的概率为：

式（6）中：Ps为nc次定检期间备用导弹数量充足的概率，可利用式（5）求得；PΔtz为从nc次定检nctc开始到值班tz时刻每座发射装置处于发射准备好状态的概率，可利用式（1）求得，即：

情况2：在第i(i=1,2,…,nc)次定检时出现备用导弹数量不足的情况，则后面不再进行定检。该种情况下每座发射装置发射准备好的概率为：

在定检时间为tc和备用导弹数量为s枚的情况下，每座发射装置发射准备好的概率为：

利用式（1）和（9），可分别得出无定检和有定检情况每座发射装置发射准备好的概率PM。由图2可知，当值班可靠度为0.80时，最长值班时间不超过4个月才能满足Pac=0.95的要求。因此，图7 a）和b）分别考察2种定检策略，即4个月和3个月定检一次时不同备用导弹数量对PM的影响。

图7 无定检和有定检情况下PM变动情况Fig.7PMchange in the absence of and without verification

由图7可知，定检能够明显提高导弹战备完好性水平，且备用导弹数量越多，战备完好性水平越高，但是随着备用导弹数量的增加，战备完好性增益在减少，备用导弹数量以2～3枚左右为宜。当备用导弹数量较多时，定检周期的长短对PM的影响不大，但在备用导弹数量较少时对PM有一定影响，且不是简单的单调递增或递减的关系。

6 结束语

本文在分析舰空导弹舰上使用剖面一般形式的基础上，以发射准备好的概率为参数，分别建立了无定检和有定检2种情况下战备完好性数学模型。通过战备完好性模型可以分析各影响因素对战备完好性的影响，如战斗值班可靠性、定检时间以及备用导弹数量等，为舰空导弹舰上使用保障方案的制定和优化提供重要理论依据。所建立的模型也可用于其他长期处于战斗值班状态装备的战备完好性评估。