基于梳状谱调制的LFM雷达噪声卷积干扰技术

赖维柯，刘 锋，李炳荣

（海军航空大学，山东烟台264001）

对雷达的有源干扰主要包括压制干扰和欺骗干扰。传统的压制干扰主要采用非相参噪声干扰，通过大功率噪声信号遮盖、淹没雷达回波信号达到干扰的目的；传统的欺骗干扰主要利用假目标迷惑敌方雷达，主要包括假目标拖引干扰、密集假目标干扰[1-3]。线性调频（Linear Frequency Modulation，LFM）雷达，通过脉冲压缩、脉冲前沿跟踪等技术，使的其对传统的压制干扰和欺骗干扰都有很好的抗干扰能力[4-6]。

为了更好地解决对线性调频雷达的干扰问题，灵巧干扰的概念随即被提出，文献[7-9]介绍了传统的灵巧干扰方法，分析了相关方法的优缺点。文献[10]指出，基于数字储频的全脉冲转发干扰虽然能获得脉压增益，形成有效假目标，但是这样会使得干扰信号至少滞后雷达回波一个脉宽，会增加平台被发现的概率；对于间歇采样干扰，文献[11]指出，该干扰方式能产生多距离假目标干扰的效果，但是该干扰只能在目标附近形成假目标，且每个假目标幅度有明显不同，无法保护载机后方的目标。同时，随机脉冲取样干扰等基于脉冲取样干扰的干扰方法得到了不少研究，但是没能根本上解决脉冲取样干扰的缺点[12-16]。

以LFM雷达为干扰对象，本文提出了一种基于梳状谱调制的噪声卷积干扰技术，利用数字储频技术得到的雷达样本与产生的梳状谱信号进行时域“乘积”调制[17-18]，将其与噪声信号进行卷积调制，所产生的干扰信号经脉冲压缩处理后，将产生大范围的噪声压制干扰和假目标干扰的效果。

该方法不仅有效解决了传统噪声压制干扰只能在主目标后面产生干扰的弊病，而且还具有大范围密集假目标干扰的能力。

1 原理分析

1.1 PD雷达灵巧噪声卷积干扰原理

记LFM雷达的发射信号为s(t)，则干扰机接收到的雷达信号为s(t-τ)，显然，s(t)、s(t-τ)是相参的。记高斯白噪声信号为n(t)，则噪声灵巧卷积干扰信号jn(t)就是s(t-τ)和n(t)的卷积，

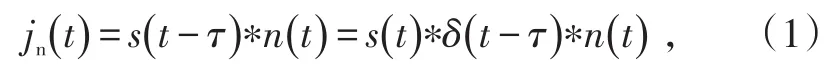
式中，∗表示卷积。

不考虑滤波器的时延，脉冲压缩滤波器的传输函数h(t)=s∗(-t)，则干扰信号经过匹配滤波器后的输出为：

设jn(t)、n(t)、s(t)的傅里叶变换分别为Jn(w)、N(w)、S(w)，时域卷积对应频域相乘，则干扰信号经过脉冲压缩后的频谱为：

因此，可以得到干扰信号经脉冲压缩后得到的时域信号为：

由此看出，噪声信号通过与截获的LFM信号进行卷积后通过脉冲压缩得到的时域输出实际上就是噪声信号与一个点扩展函数的卷积，通过这种方式，干扰信号得到了脉冲压缩增益，相对于传统噪声干扰将会对LFM雷达具有更有效的压制干扰效果。

1.2 LFM雷达的梳状谱干扰原理

对LFM雷达的梳状谱干扰主要通过数字储频技术将得到的雷达信号与梳状谱信号进行乘积调制，从而产生多假目标欺骗干扰的效果，其中每个假目标出现的频点就是梳状谱信号对应的频点。由于干扰信号具有相参性，因而也能起到一定的干扰效果。

设comb(t)是包含K个频点的梳状谱信号，表达式为：

式（5）中：fk为第k个频点的频率值；ak为第k个频点的幅度值。

记LFM雷达发射的线性调频信号s(t)表达式为：

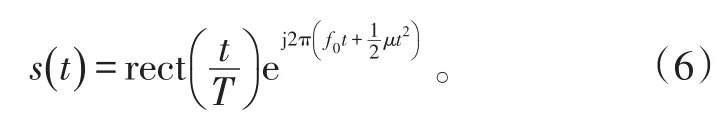
式（6）中：T为信号时宽；f0为信号中心频率；μ=B/T是调频斜率，B为信号带宽。

因此，通过将线性调频信号与上述梳状谱信号进行乘积调制，可以得到对LFM雷达的梳状谱干扰信号的表达式为：

脉冲压缩滤波器的传输函数：

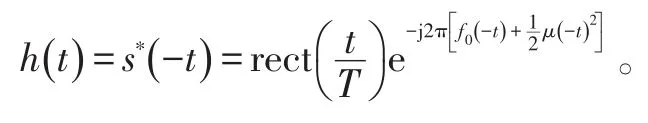
干扰信号通过脉冲压缩后得到的时域信号jpc(t)为：

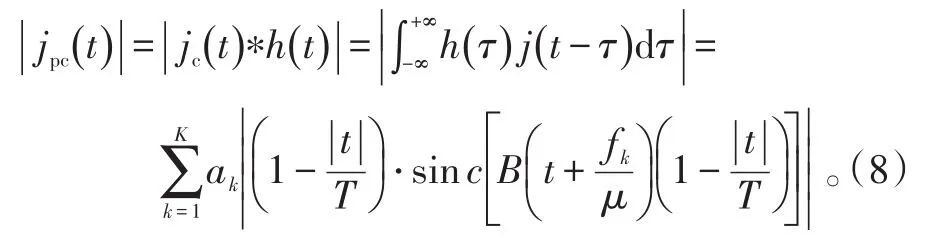
由此看出，梳状谱干扰信号经过脉冲压缩后的输出是K个辛格函数加权之和，且当t+fk/μ=0，即t=-fk/μ,k=1,2,…,K时，会出现峰值，刚好对应K个假目标所产生的时刻。据此根据fk的正负值，就可以同时形成前置、后置假目标，达到更好地假目标欺骗干扰的效果。

1.3 LFM雷达基于梳状谱的灵巧噪声压制干扰

从1.1节和1.2节的分析可以看出，无论是单独的梳状谱干扰，还是灵巧噪声干扰对LFM雷达的干扰都不是足够有效，但是如果利用梳状谱干扰产生一些前置、后置假目标。然后，在进行噪声卷积调制，就可以产生大范围的灵巧噪声压制干扰效果。

式（7）与高斯白噪声n(t)卷积得到梳状谱灵巧噪声干扰信号为：

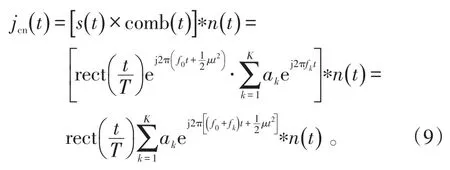
因此，通过脉冲压缩滤波器，得到梳状谱灵巧噪声干扰信号的输出为：

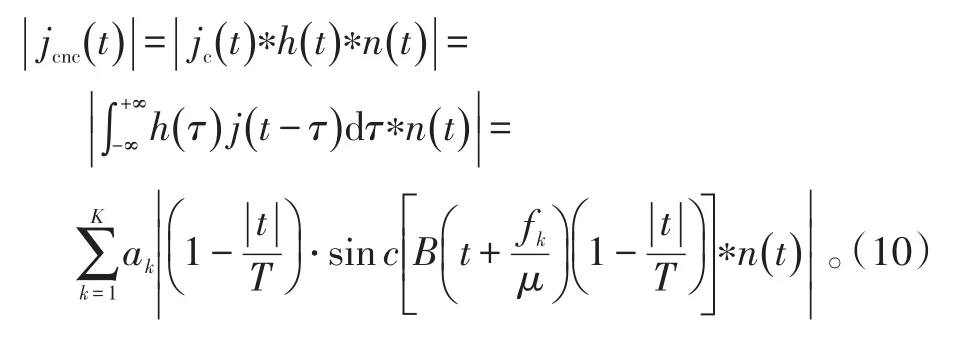
普通的灵巧噪声干扰，在经过脉冲压缩后将会在真实目标之后产生干扰效果，因此很容易就能被识别。但是由式（10）可以看出，利用梳状谱灵巧噪声干扰通过脉冲压缩之后将会在每个假目标之后都产生噪声干扰的效果，因而只要设置前置假目标与后置假目标混合，将会产生大范围的噪声干扰效果，将会进一步提升干扰效果。

2 干扰效果仿真与分析

2.1 LFM雷达的灵巧噪声卷积干扰仿真

取LFM雷达所发射的线性调频信号带宽B=1 MHz，脉宽 PW=100 μs，调频斜率k=10 G ，噪声功率为1dB，采样频率为100 MHz，通过仿真得到对PD雷达的噪声卷积灵巧干扰效果如图1所示。

由图1可以看出，采用噪声卷积干扰确实能起到很好的压制效果，同样也可以看出，真目标的位置正好出现在100 μs处，而干扰效果也正好从真目标开始向后展开，呈现一系列前置干扰效果。因此，能轻易找到目标的位置，且这种干扰方式在实战中无法保证有效性。

图1 噪声卷积干扰效果Fig.1 Noise convolution effect diagram

2.2 LFM雷达的梳状谱干扰仿真

取梳状谱信号的各个频点依次为：±500 kHz、±200 kHz、0，线性调频信号参数不变，每个频点对应幅值加权系数为：2、1.25、1；得到干扰信号经过脉冲压缩后的输出如图2所示。

图2 LFM雷达的梳状谱干扰效果示意图Fig.2 Comb spectrum interference effect of LFM radar

由图2可以看出，对应每个梳状谱信号的频点，都会有一个假目标与之一一对应出现，且相邻假目标的时间间隔为Δt=(fk-fk-1)/μ,k=2,3,…,K。一方面，LFM雷达的距离分辨率可以用1/B来衡量，这也就是说如果Δt＞1/B，将会形成可分辨的距离假目标，产生的假目标越多，欺骗干扰的效果也越好；如果Δt＜1/B，那么假目标之间是不能区分开来的，这样就会形成压制干扰的效果。另一方面，这种干扰方式存在的问题在于，要想取得好的干扰效果就需要足够度的假目标，这就要求梳状谱的数目足够多，这就导致干扰信号的平均功率大大降低，反而不利于干扰。

综上所述，单纯的梳状谱干扰无论是从欺骗干扰角度还是压制干扰角度，都受到梳状谱的数目和功率的限制，存在一定的局限性。因而基于梳状谱的灵巧噪声卷积干扰正好弥补了这一切。

2.3 LFM雷达的基于梳状谱的灵巧噪声干扰仿真

雷达发射信号保持不变，梳状谱频点也保持不变，噪声功率取1dB，得到梳状谱噪声卷积干扰信号经过脉冲压缩后的输出如图3所示。

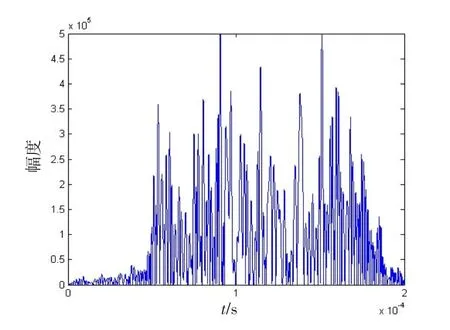
图3 LFM雷达的基于梳状谱的灵巧噪声卷积干扰效果Fig.3 Smart noise convolution jamming effect based on comb spectrum of LFM radar

由图3可以看出，调制梳状谱信号的灵巧噪声信号经过脉冲压缩将会产生大范围的压制干扰效果和密集假目标干扰效果。可以看出，通过合理设置梳状谱信号的频点产生前置假目标，再用噪声卷积干扰，就可以产生覆盖真实目标的噪声压制效果。这样做，不用太多的频点，将梳状谱信号的频点间隔拉的越大，干扰范围也越大。这样就可以同时避免普通噪声卷积干扰的弊端和单独梳状谱干扰分散太多功率的弊端。

3 硬件实现

调制梳状谱信号可以用一块中频信号处理模块，天线接收到雷达回波（干扰信号）后，先通多下变频将信号变换到中频进再行数字化处理。可以用现场可编程门阵列（FPGA）+数字信号处理芯片（DSP）实现中频信号数字处理。FPGA的功能主要包括数字正交下变频、数字储频、产生所需的梳状谱信号、调制梳状谱信号、数字正交上变频等功能。DSP的作用是接收干扰指令，计算干扰参数和产生相应频点的干扰信号、DRFM的读写控制等功能。用梳状谱信号调制后，再接入一个卷积器，将噪声产生模块产生的噪声与梳状谱调制信号进行卷积就得到了我们所需的基带干扰信号。

具体干扰信号的实现如图4所示。

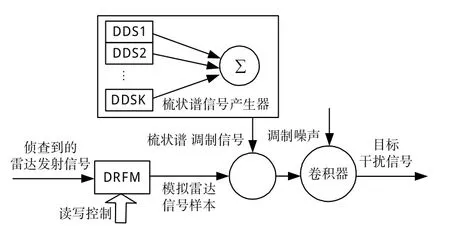
图4 干扰硬件实现方案Fig.4 Interference with hardware implementation

通过将FPGA中的直接数字频率合成器（DDS）单元进行组合就可以产生基带梳状谱信号，每个DDS根据FPGA中计算出的梳状谱的相应参数实时产生同相（I）、正交（Q）两路基带信号，之后将每个DDS的输出信号相加后再与雷达发射信号的相参样本的基带I、Q信号进行时域“乘积”调制，之后分别与噪声信号进行卷积调制，就能产生干扰数字基带I、Q信号。硬件上只需1个单级存储器、K个DDS、K-1个加法器、1个乘法器、1个噪声产生器和1个卷积器，就可以产生具有K个具备前置掩护能力的假目标灵巧噪声干扰信号，消耗资源小，便于工程实现，干扰效果也好。

4 结束语

对PD雷达的基于梳状谱的灵巧噪声卷积干扰通过梳状谱频点的控制可以产生前置假目标，与噪声结合，就会产生大范围的噪声压制干扰效果，最后将会形成假目标与压制干扰2种效果。这种干扰方式效果好，不需要太多梳状谱频点数，需要器件较少，是一种比较好的干扰方式，有较强的工程应用价值。