一类电子评标算法的安全性分析

赵 国

( 西南民族大学计算机科学与技术学院，成都 610041)

引 言

电子评标算法是整个电子评标系统的核心所在，其算法性能不仅影响评标结果的公平和公正，而且直接关系到招标、投标各参与方的合法权益［1］。

已有的招标、投标策略的研究多集中于各投标人的成本分布函数，通过计算博弈均衡以确定最优报价［2-10］，此法没有考虑电子评标算法本身具有的特征，因而存在一定不足。例如，在工程量清单招标中，工程数量是给定的，这意味着各标书的投标报价是综合单价的线性函数，如果投标人事先知道招标文件中公布的电子评标算法也存在线性结构，那么他可能会联合部分投标人私下串通投标报价，利用电子评标算法本身的潜在缺陷影响甚至控制最低评标价，从而损害招标人或者其他投标人的合法权益。当然，串通投标报价的行为违反了《中华人民共和国招标投标法》，但若是电子评标算法本身存在缺陷，则对此类违法行为防不胜防。

该算法作为评标算法的附件见于《绵阳市国家投资工程建设项目房屋建筑及市政工程标准施工招标文件( 2010 年版) 》［11］。虽然在最新版《绵阳市国家投资工程建设项目房屋建筑和市政工程施工标准招标文件( 2017) 》［12］中，没有继续推荐使用该算法作为评标价算法，但该算法的一个改进版本被《深圳市建设工程施工招标文件示范文本( 2012. 06 版) 》［13］采用。

在这一类基于价格要素偏差率的电子评标算法中，标书的偏差率是由价格构成要素( 人工费、材料费、机械费、综合费、措施费及其他费) 的偏差率直接加权平均折算而成的，其权重为各价格构成要素占总报价的比重。这种标书偏差率的线性加权结构意味着标书偏差率只与价格构成要素的算术平均值有关，而与其取值分布无关，这就使得投标人有机会进行串通投标报价，调整非法标书中各价格构成要素的值，使得这些非法标书在形式上是合法的。因此，本文旨在对一类基于价格要素偏差率的电子评标算法进行安全性分析，将利用这种线性结构来设计一种围标算法，并对其进行理论分析，从而论证其存在的安全隐患。

1 基于偏差率的电子评标算法

评标是体现招标投标公平合理的核心环节。在工程量清单计价模式下的招标中，评标价的计算是电子评标的关键。

1.1 工程量清单

工程量清单是建设工程的分部分项工程项目、措施项目、其他项目、规费项目和税金项目的名称和相应数量等的明细清单［14］。以分部分项工程量清单与计价表为例，见表1。

表1 分部分项工程量清单与计价表

在工程量清单招标中，工程数量是给定的，这意味着各标书的投标报价是综合单价的线性函数，正是这种线性结构使得基于价格构成要素偏差率的电子评标算法存在安全隐患。

为方便起见，本文将以表1 中的分部分项工程量清单为例，研究一类基于价格构成要素偏差率加权平均的电子评标算法的安全性能。

1.2 评标价计算方法

在电子评标算法中，计算机评标系统按照“投标报价评审算法”，自动对各投标人的投标报价进行详细评审，并计算出评标价。以经评审的最低投标价法为例［11］，评标价的计算方法如图1 所示。

在基于偏差率的评标价计算方法中，评标价的计算由如下步骤构成:

(1) 逐项确定招标文件中所有清单项j = 1，2，…，n的价格构成要素( 人工费、材料费、机械费、综合费) 的基准值。按照招标文件约定，如果标书数量m ≥20 ，基准值的取法按照正态分布取值。以清单项j 的人工费为例，从m 份标书中去掉离散样本值后，剩余样本数值的算术平均值即为清单项j 的人工费的基准值。

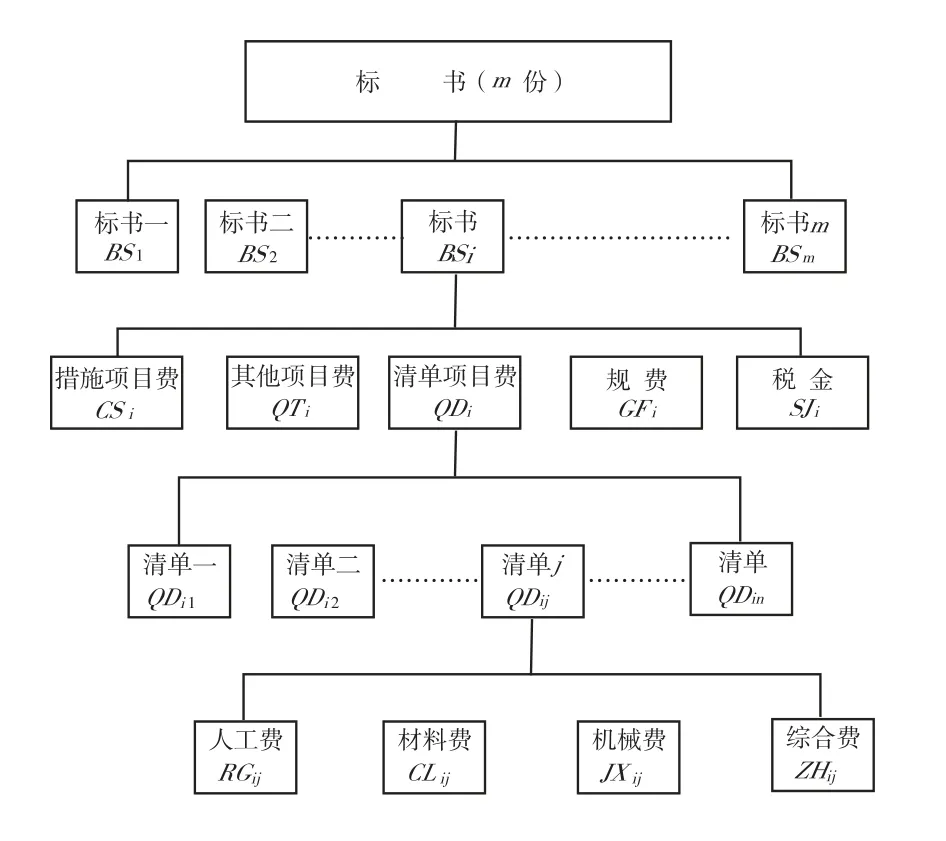
图1 投标报价评审算法

(2) 逐一计算所有投标文件中清单价格构成要素( 人工费、材料费、机械费、综合费) 的偏差率PRGij，PCLij，PJXij，PZHij。对每个清单项j 的价格构成各要素，均要计算其偏差率。以标书i 中清单项j 的人工费为例，其偏差率为:

(3) 计算标书i 的清单偏差率。将每个清单的价格构成要素的偏差率，按照其在清单价格中的比重，加权平均折算到清单偏差率中。例如，标书i 中清单项j 的偏差率为:

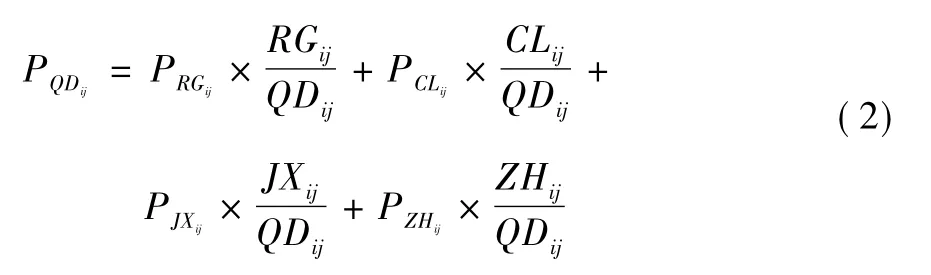
( 4) 计算标书i 措施费的偏差率PCSi。方法是按照各投标文件措施费总价( 扣除不可竞争费后) 进行计算。

(5) 计算标书i 其他费的偏差率PZi。方法是按照各投标文件投标报价( 扣除不可竞争费后) 进行计算。

(6) 计算标书i 的偏差率PBSi。方法是将清单偏差率、措施偏差率与其他费用偏差率这三项按照清单费用、措施费用和其他费用占总报价的比重，经加权平均折算到标书偏差率中，即:

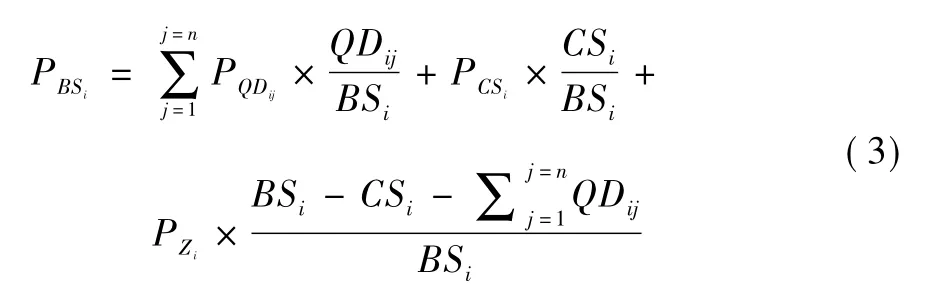
(7) 计算标书i 的评标价

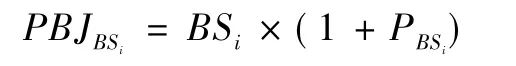
根据最低投标价法，将所有投标人的评标价按照由低到高的顺序进行排序，评标委员会从其中推荐1 ～3名作为中标候选人。

2 围标算法

1.2 节中基于偏差率的电子评标算法的设计初衷是尽可能以合理低价中标，但是这个算法本身存在严重缺陷，这种缺陷主要存在于下述两种设计中。

第一，招标文件中所有清单项的价格构成要素( 人工费、材料费、机械费、综合费) 的基准值，等于从所有标书中去掉离散样本值后，剩余样本数值的算术平均值。但是，根据大数定律［15］，当标书数量m ≥30 时，这个算术平均值应非常接近该要素的市场价格，从而很容易由市场价格来进行估计。以表1 中清单项001( 砌墙) 为例，根据大数定律，所有合法标书人工费的算术平均值应非常接近其市场价格978 元，如果所有标书都是合法的，在基于偏差率的评标算法中，清单项001 的人工费基准值应满足

第二，标书的偏差率是由价格构成要素( 人工费、材料费、机械费、综合费、措施费、其他费) 的偏差率经直接加权平均折算而成，其权重为各价格构成要素占总报价的比重。这种线性加权结构使得评标算法的安全性极为脆弱，容易被操纵。因为，线性加权结构意味着: 只要标书i 的所有价格构成要素的偏差率同时达到最小，则标书的偏差率PBSi自然达到最小，根据大数定律，该标书的评标价就能大概率地成为最低评标价。

下面，将分析这两个设计缺陷如何导致基于偏差率的评标算法被人为操纵的。本文将证明，只需一小部分( 理论阈值为20%，推导见后面的3.2 节) 投标者串通投标报价，就可以大概率地使指定标书的评标价达到理论最小值。

假设标书数量为m，其中标书1，2，…，n 已串通投标报价，打算让标书1 以最低评标价成为中标候选人。那么，利用大数定律以及评标算法的线性结构，可以通过以下步骤将标书1 的偏差率控制为最小，从而实现中标目的。注意，此时只有标书n + 1，n + 2，…，m 是合法的。

第一步研究招标文件，熟悉投标人须知中的各项要求及各种评标算法参数。

例如，《绵阳市招标文件(2010 年版) 》［11］规定:

(1) 投标人的报价低于招标控制价80%和高于招标控制价的投标报价，直接废标，不进入下一步评审。

(2) 当投标人的投标报价低于招标控制价的85%并且低于所有投标人( 不含(1) 中所述的直接废标的投标人的投标报价) 投标报价算术平均值的95%时，该投标人的投标报价将被认定为低于成本报价，作废标处理。

投标人不会冒直接废标的风险，也就是说，他们可以合理地假设投标人的总报价都不低于招标控制价的85%。为方便起见，称投标人须知中d = 0.95 为控价因子。

第二步进行市场调查，确定各清单项的价格构成要素( 人工费、材料费、机械费、综合费) 的市场价格，在此基础上，确定标书1 的总报价。

以表1 中清单项001( 砌墙) 为例。假设通过市场调查，得知人工费的市场价格的极大似然估计值为978。根据大数定律，当标书数量m ≥30 时，所有合法标书人工费的算术平均值应非常接近

为了不成为废标，所有投标人的报价都会根据招标控制价进行成比例调整。为简便起见，假设招标控制价高于市场成本。在此情形下，直接以市场价格报价不会成为废标，所以设标书1 的清单项001 的人工费为RG11需要指出的是，此时标书1 的报价在形式上是完全合法的。

第三步利用大数定律，制作非法标书，控制标书1的清单偏差率最小。

首先考虑清单项目中人工费的偏差率，以清单项001( 砌墙) 为例。投标人1 串通投标报价投标人2，3，…，n，制作n－1 份非法标书，理论上可以控制这n－1份非法标书中清单项001 人工费的算术平均值RG～1，使得标书1 的人工费偏差率达到理论最小值。

要让标书1 不成为废标，投标人1 的投标报价不能低于所有投标人投标报价算术平均值乘以d，也就是说，至少要让m 份标书( 包括非法的) 清单项001 的人工费算术平均值满足以下条件:

利用大数定律很容易做到这一点。事实上，根据大数定律，当合法标书数量m ≥30 时，m － n 份合法标书人工费的算术平均值应非常接近由此可得式(5) :

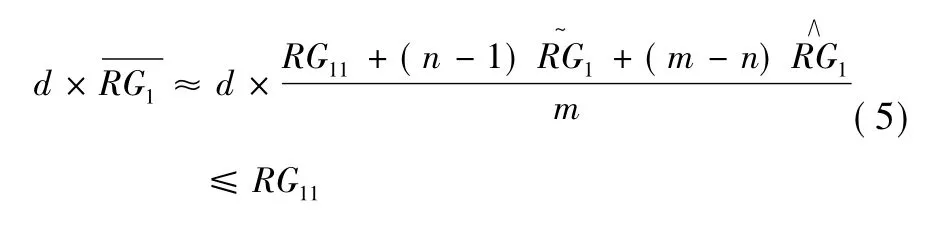
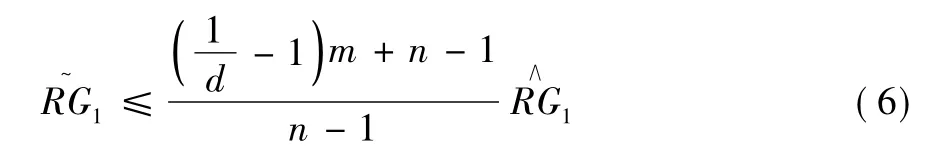
特别地，令控价因子d = 0.95，则得:

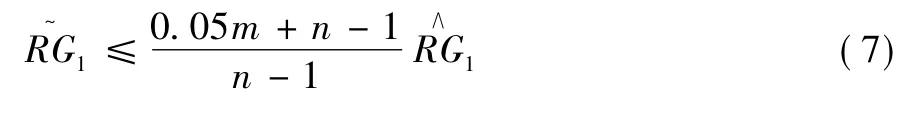
这里只需要控制n －1 份非法标书中清单项001 人工费的算术平均值而对其取值分布没有任何要求，这就使得投标人1，2，…，n 可以串通投标报价，通过调整标书2，…，n 中清单项001 人工费的值，使得这些非法标书在形式上是合法的。

同理，可以控制标书1 的其他清单项的人工费偏差率达到最小。通过这样的方法来制作非法标书，控制标书1 的所有清单项的材料费、机械费、综合费偏差率同时达到最小，从而保证标书1 的清单偏差率达到理论最小值。

第四步利用标书偏差率算法的线性加权性质，制作非法标书，控制标书1 的偏差率PBS1达到最小。

在基于偏差率的电子评标算法中，标书的偏差率是由清单偏差率、措施偏差率、其他费用偏差率经直接加权平均折算而成，其权重为各价格构成要素占总报价的比重。这种线性加权结构使得评标算法的安全性即为脆弱，容易被操纵。因为，线性结构意味着: 只要标书1的所有价格构成要素( 人工费、材料费、机械费、综合费、措施费、其他费) 的偏差率同时达到最小，则标书的偏差率PBS1自然达到最小，就能大概率以最低评标价中标。

同时，标书偏差率的线性加权结构意味着标书偏差率只与各价格构成要素( 人工费、材料费、机械费、综合费) 的算术平均值有关，而与其取值分布无关，这就使得投标人1，2，…，n 可以串通投标报价，调整非法标书2，…，n 中各价格构成要素的值，使得这些非法标书在形式上是合法的。

3 围标算法分析

验证上述分析结论的最好实证方法是根据理论分析的结果来制作一些非法标书，然后通过电子评标系统的评标结果来进行检验。同时，必须要指出的是: 这种行为是违法的，任何试图利用本文研究成果进行招投标的非法行为都将承担相应的法律后果。

如果不采用实证方法来验证，则退而求其次，可对理论模型中的参数进行数值分析，针对的关键问题是:非法标书是否能保证形式上合法而不直接废标。理论上讲，标书偏差率的线性加权结构意味着标书偏差率只与各价格构成要素( 人工费、材料费、机械费、综合费、措施费、其他费) 的算术平均值有关，而与其取值分布无关，但是这些取值可能受评标算法参数的影响较大。

3.1 控价因子

招标控制价直接影响投标人的利润水平以及投标策略，同时也影响非法投标人的违法成本。

例如，《绵阳市招标文件( 2010 年版) 》［11］中规定，投标报价不能低于所有投标人投标报价算术平均值乘以d = 0.95。若重新规定控价因子d = 0.9，则可以得出非法标书中清单项001 人工费的算术平均值应满足:

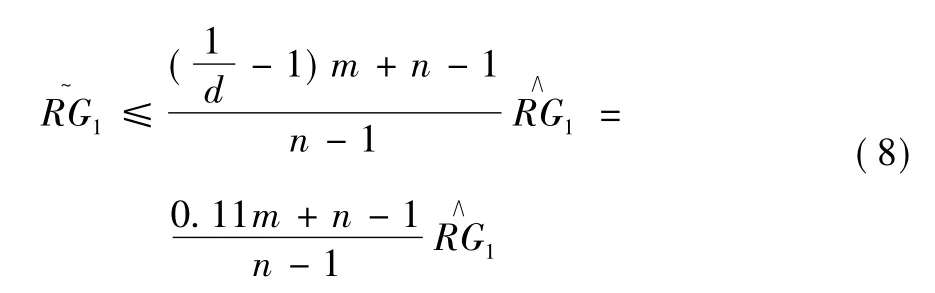
由此可见，随着控价因子的减小，非法标书1 成为废标的风险增大了，相应地，围标的违法成本也增大了。

3.2 参与围标的标书数量

参与围标数量n 的多少直接决定了其违法成本。很显然，如果很少的一部分投标人串通投标报价就可以控制评标结果，那么这个评标算法就存在重大安全隐患。

例如，《绵阳市招标文件( 2010 年版) 》［11］中规定，投标人的报价低于招标控制价80%和高于招标控制价的投标报价，直接废标。在此规定之下，如果报价高于市场价的倍，则极有可能超出招标控制价。要想形式上合法，非法标书中清单项001 人工费的算术平均值的最大值应满足:

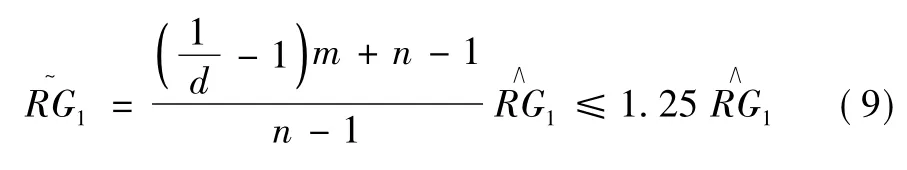
解之得:

特别地，令控价因子d = 0.95，得:

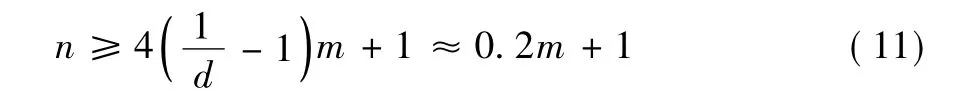
由此并结合大数定律，可得出结论: 最少只需要20% 的投标人相互串通报价，就可大概率地确保中标。

实际上，本文只讨论了n 家投标人联合而确保1 份标书入围中标候选人的情形。事实上，若将标书1 中价格构成要素加入白噪声而“复制”多份，则实现围标的概率将更大，所以，基于偏差率的电子评标算法存在重大安全隐患。

4 结束语

电子评标算法是整个电子招标系统的核心所在，其安全性能直接关系到评标结果的公平和公正。本文对一类基于价格构成要素偏差率加权平均的电子评标算法进行安全性分析。理论分析表明，在算法参数已知条件下，投标人可以私下串通报价，从而影响招标文件中所有清单项的价格构成要素的基准值，进而控制指定标书的偏差率。根据大数定律，小部分投标人采用串通投标报价的围标策略就能大概率地使指定标书的评标价达到理论最小值，进一步的数值分析表明，在《绵阳市招标文件( 2010 年版) 》给定的参数条件下，最少只需要20% 的投标人相互串通投标报价，就可大概率保证指定标书成为中标候选人。此研究结果将有助于确保招标投标各方的合法权益。