谱元法在多层粘弹性路基中位移计算的研究
汪昌勇,冯志强,李九一,陈荟键
( 西南交通大学力学与工程学院,成都 610031)
引 言
目前,在数值模拟方面,对大多数固体模型进行分析的方法通常是有限元法、边界元法等。在公路工程中,路基检测的方法一般分为两种,一种是钻取样本检测方法,另一种是无损检测法[1]。无损检测方法中的落锤式弯沉仪( Falling Weight Deflectometer,FWD) 检测方法,是通过落锤式弯沉仪对路面施加瞬态载荷( 该载荷可以很好的模拟行车载荷) ,并通过电脑获取传感器数据,进而分析公路质量的一种方法[2-3]。落锤式弯沉仪检测能够在短时间内获取数据并进行分析,适用于对公路的阶段性检测,能够及时得出公路质量结果,节约公路养护资金,减少交通事故的发生[4]。高速公路结构一般分为路面层、基层和底基层[5]。按路基性质区分,公路分为刚性路基、柔性路基和半刚性路基[6]。Al -Khoury 等人[7]通过对路基结构的研究,提出了一套新的理论方法即对线弹性多层结构进行计算和分析的谱元法理论。谱元法的基本思路是首先基于连续介质力学得到结构的受力平衡偏微分方程;然后利用傅里叶变换将时域内的偏微分方程转化为频域内的常微分方程;其次通过引进波谱形函数,把单元的任一位置的位移用结点位移表示;最后求解常微分方程并代入相应的载荷和边界条件,求出位移以及其它的变量结果,并将结果转化为时域中的结果[8]。工程中,路基层常常表现出粘弹性,本文以线弹性得到的谱元法理论为基础,对粘弹性层结构模型进行分析,这可为结构的参数识别方法打下坚实的基础。
1 谱元法理论
柱坐标系下的半空间如图1 所示,图中虚线表示理想边界,该处路表响应为零; p( r,t) 为施加的瞬态载荷,可用点关于空间和时间两个独立函数的乘积表示,其表达式为:

对于各向同性线弹性体,以位移表达的纳维方程为:
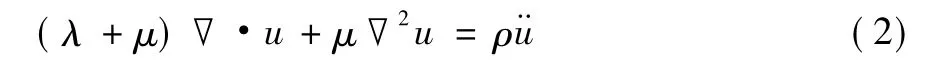
式中u 为弹性体的位移; ρ 为弹性体的质量密度; λ 和μ为拉梅常数。
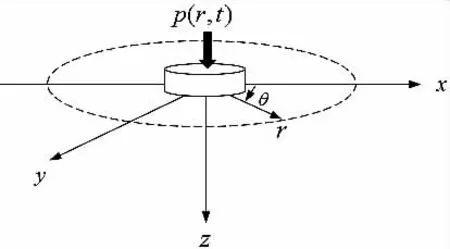
图1 柱坐标系下的半空间
根据斯托克斯-亥姆霍兹矢量分解定理,位移矢量场可用标量势函数φ( r,t) 和一个矢量势函数珗ψ( r,t) 表示:
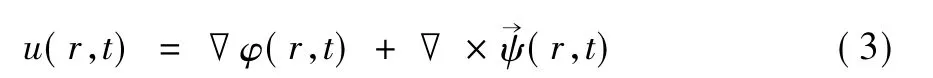
1.1 轴对称结构的求解推导
由于轴对称性质,以势函数表示的位移表达式和应力-位移表达式分别为:
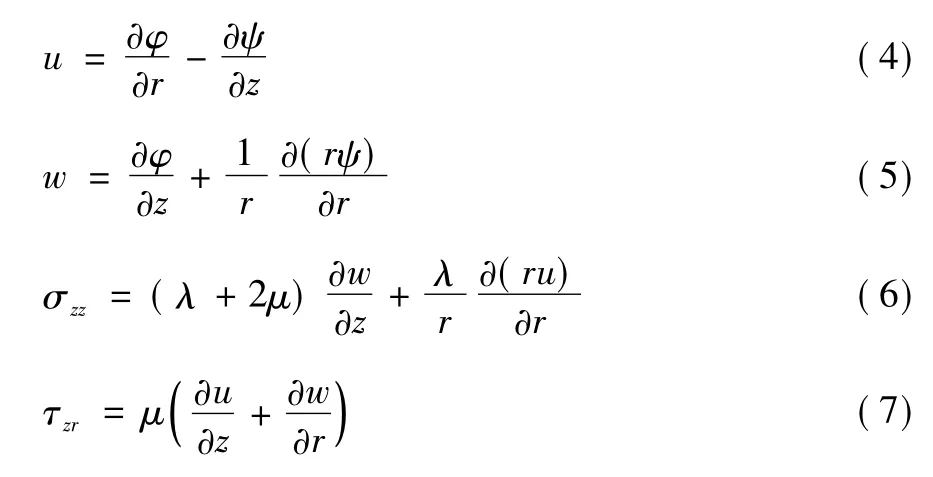
式中u 和w 分别表示水平位移和垂直位移。将式(4) 和式(5) 代入式(2) ,通过傅里叶变换得:
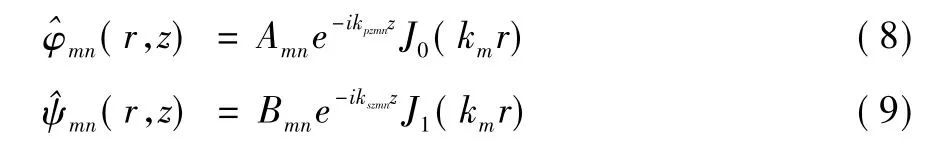
通过求和得到:
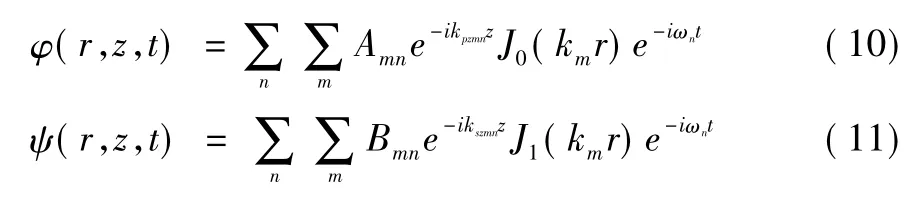
对于给定边界r = R,n = 1,...,N; m = 1,...,M就足够能描述模型整体的振动形态。于是:
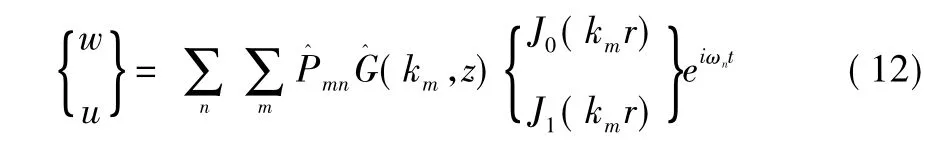
Doyle[9]将谱元法运用于轴对称单元,得到了两种类型的单元,即二节点层单元和一节点半空间单元。二节点轴对称层单元如图2 所示。
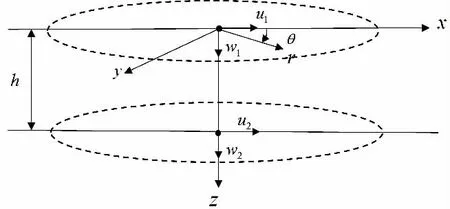
图2 二节点轴对称层单元
由于二节点轴对称层单元具有入射波和反射波的叠加,因此,其位移表达式为:
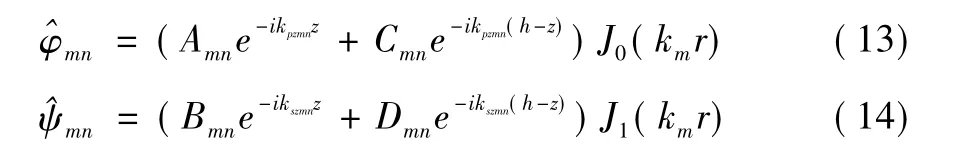
仅考虑垂直方向,则有:
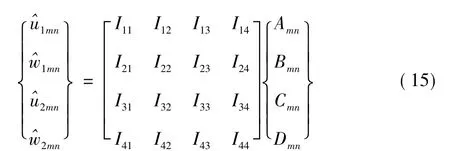
式中:
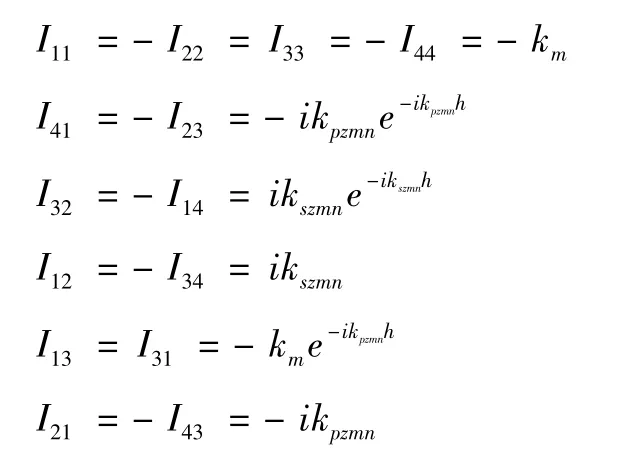
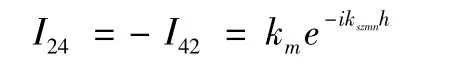
于是可知系数Amn、Bmn、Cmn和Dmn由上述节点位移确定,令式(15) 中的4 × 4 的逆矩阵为因于是有:

根据柯西应力原理[10],正应力、剪应力与边界应力的关系为Tk= τkmnm,其中单位矢量n 是垂直于界面且指向外侧的,于是有:
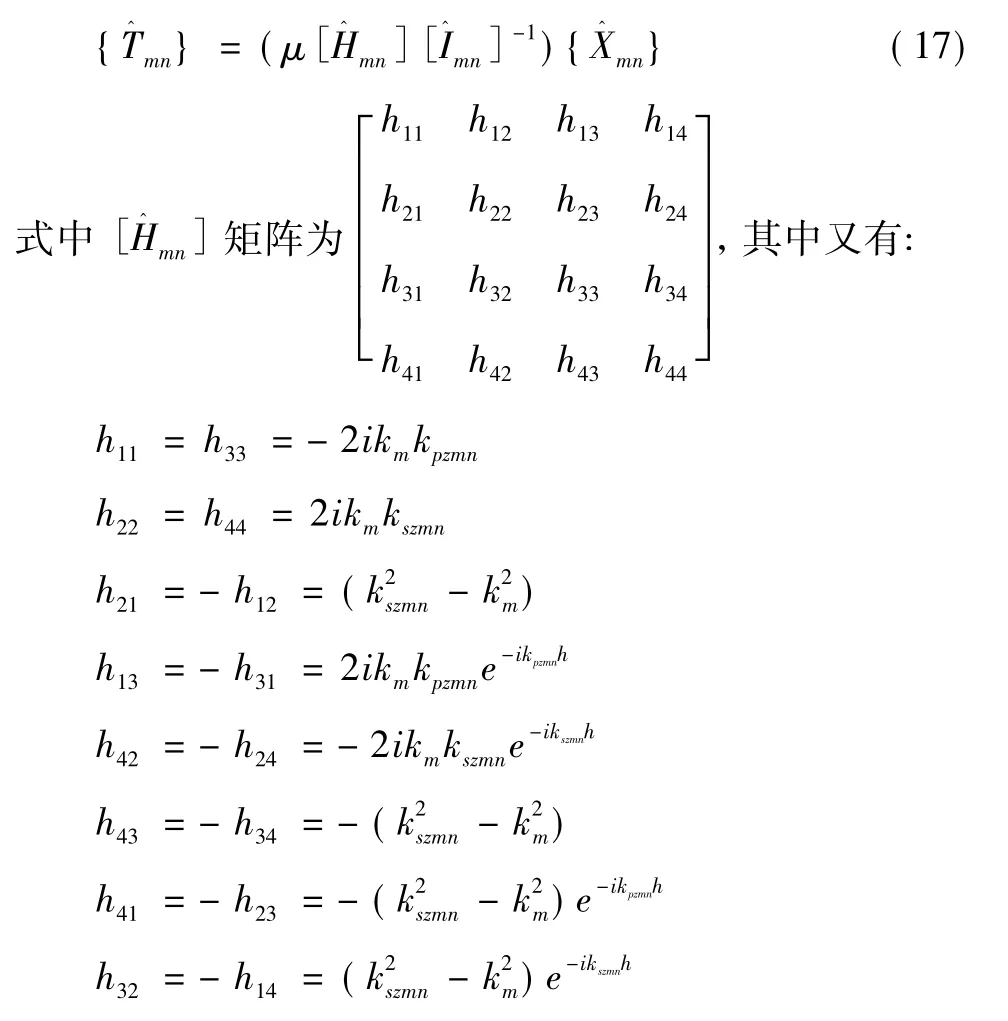
一节点半空间单元属于二节点层单元的特例,如图3 所示。由于没有反射波的产生,因此得出:

式中:
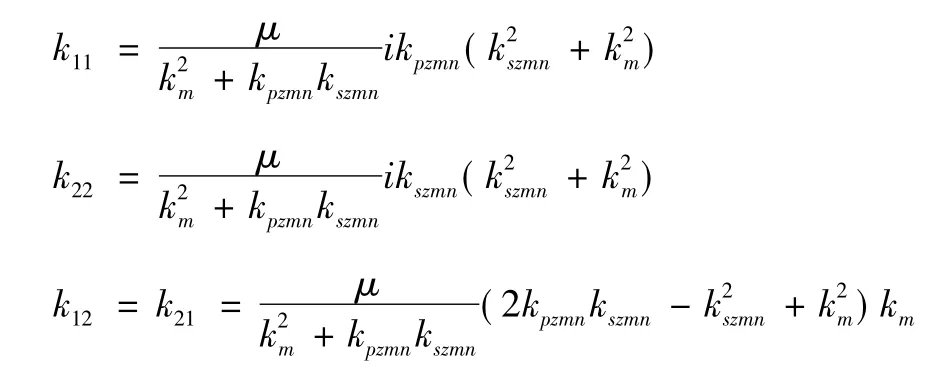
式(18) 中的二阶矩阵即为一节点半空间单元的刚度矩阵。
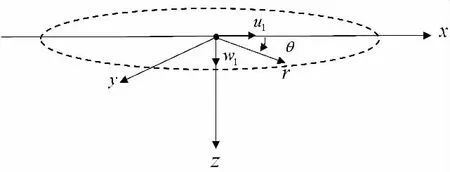
图3 一节点半空间轴对称单元
根据库利-图基的基2 快速傅里叶算法[11],离散傅里叶变换对为F( t) 和:
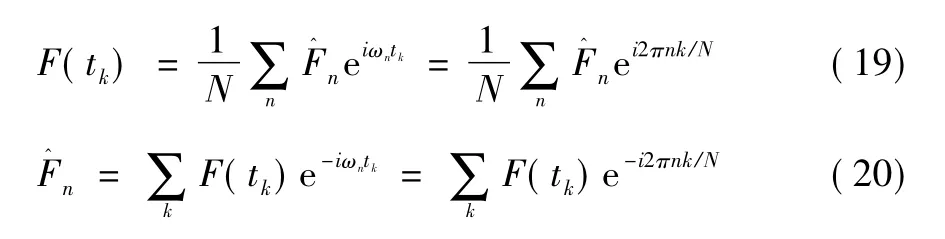
式中,k,n = 0,1,...,N -1 ; N 是奈奎斯特频率的采样数; tk= k·Δt,Δt 是采样间隔。
载荷分布形态如图4 所示。对于一个圆柱形载荷,它的半径为a,q = 1,那么载荷的空间分布表达式可以写为:
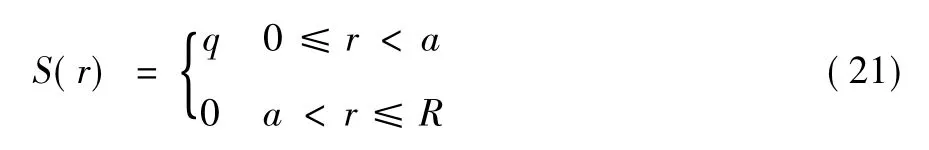
于是根据傅里叶—贝塞尔理论[12],可以确定为:
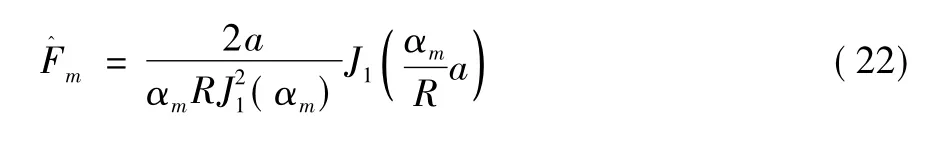
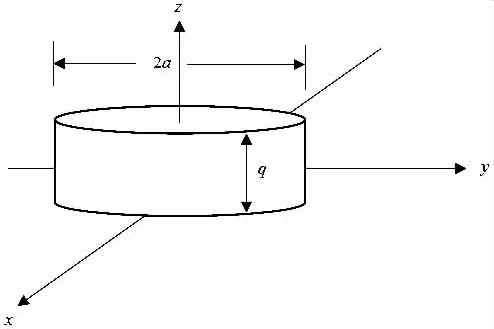
图4 载荷分布形态
1.3 刚度矩阵组装
谱元法刚度矩阵结构单元划分的示意图如图5 所示。
从图5 可知,谱元法刚度矩阵的结构包含2 个有限厚度层和1 个半无限层,分别以2 个二节点单元和1 个一节点半无限单元组成,一个单元模拟一整层。谱元法刚度矩阵km,ωn) 的组装原理类似于有限元法中刚度矩阵的组装[13]。谱元法刚度矩阵总方程组为:
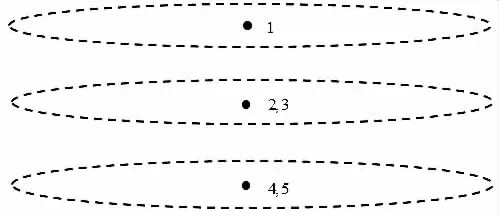
图5 结构单元划分的示意图
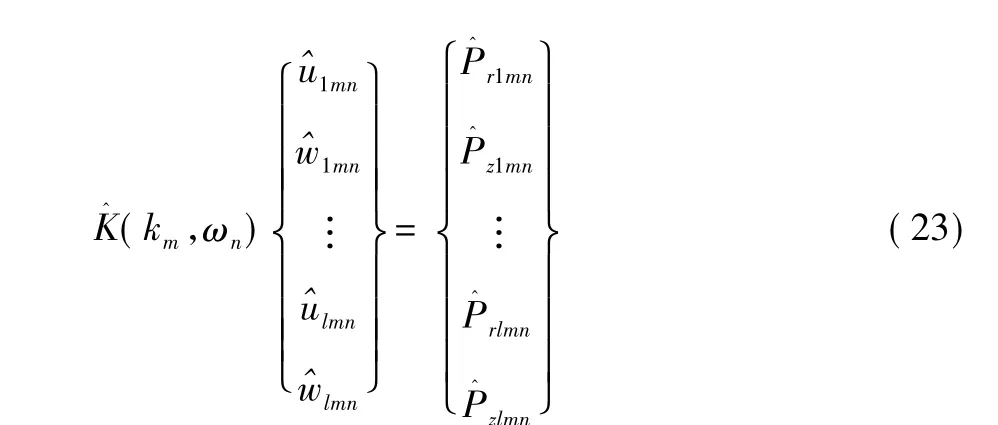
式中:
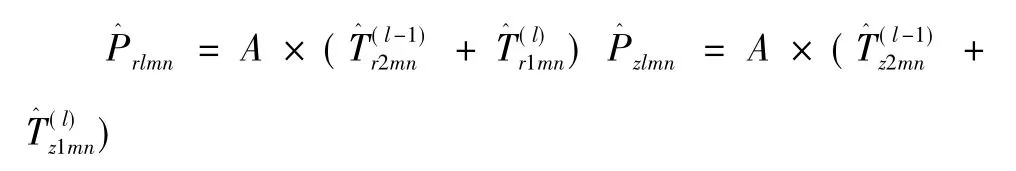
通过求和并逆变换得:
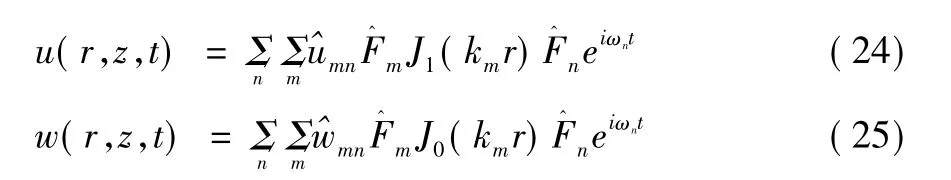
1.4 谱元法小结
传统有限元法对模型划分单元数很多,所需计算时间较长,而谱元法计算过程主要在频域中,避免了遇到无穷积分的计算难题,且谱元法的二节点层单元可以模拟整个路基层,一节点单元可以模拟半无限路基层,因此在划分单元上,谱元法优于有限元法。
2 粘弹性介质
2.1 偏微分算子法
粘性对粘弹性介质中波传播的影响很大[14]。线性粘弹性固体可以利用胡克定律得到应力和应变关系,采用偏微分算子法,应力和应变表达式为:

将式(26) 傅里叶变换得到:
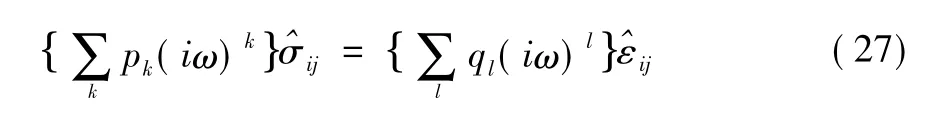
2.2 伯格斯(Burgers)模型
伯格斯模型是将Maxwell 模型和Kelvin 模型联合一起的模型,如图6 所示。伯格斯模型能很好的模拟粘弹性的特性[15]。
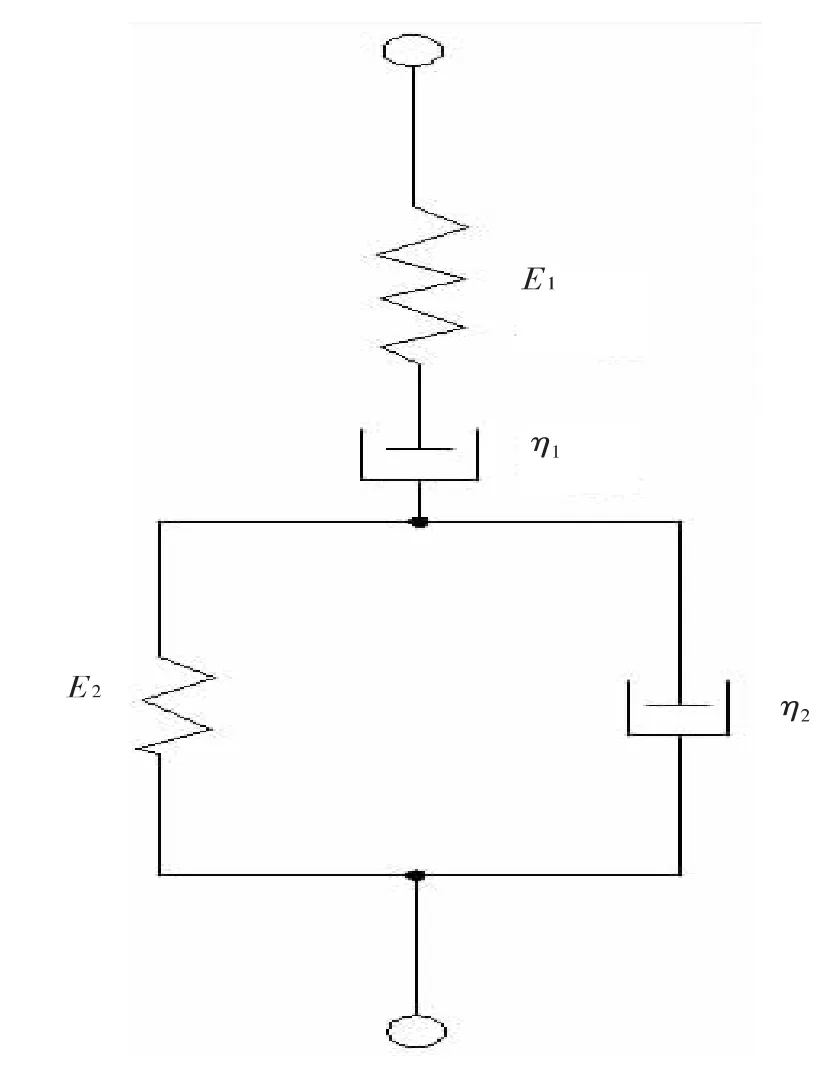
图6 伯格斯(Burgers)模型
伯格斯模型的应力-应变表达式为:
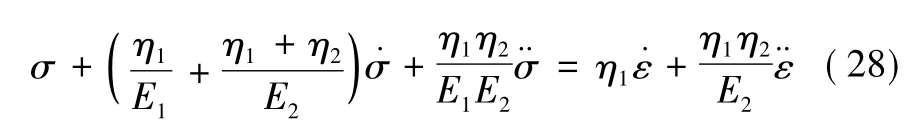
由式(27) 和式(28) 得到:


式中,E*( ω) 为伯格斯模型复模量。这里假设材料对体积行为表现为弹性可压缩( σii= 3Kεii) 以及多维变形的伯格斯行为( Sij= 2μ*( ω) eij) ,于是有:
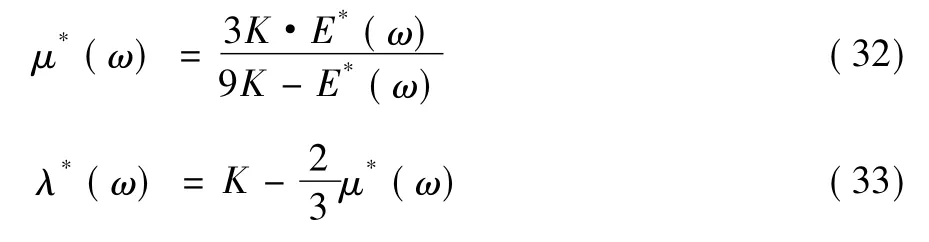
式中,K 为体积模量。对于粘弹性层刚度矩阵,需要将线弹性公式(17) 中的μ 替换成式(32) 中的μ*( ω) ,然后通过组装单元刚度矩阵得到其总体刚度矩阵。
2.3 程序计算流程
程序计算流程如图7 所示。
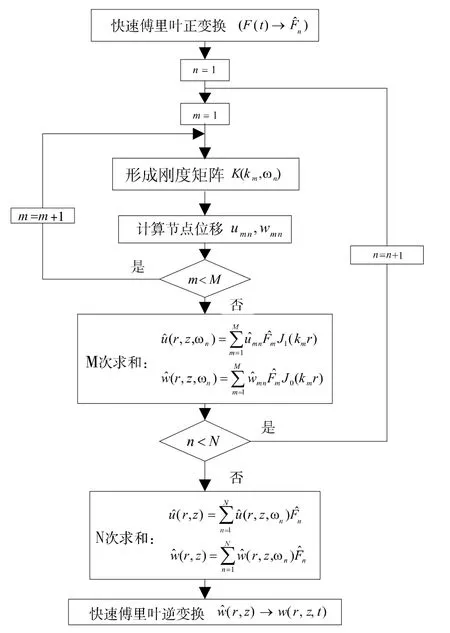
图7 程序计算流程图
首先通过使用编程软件自编程序代码;然后通过计算程序计算得到模型表面不同位置的垂直方向位移的数据;最后将数据导入绘图软件中,获取数据曲线并对其进行分析。
3 算 例
Al-Khoury[7]等人通过谱元法对线弹性层的计算做出了验证,将计算结果与有限元软件CAPA -3D 的计算结果作对比,证明了谱元法对线弹性层计算的精确性和适用性。对于粘弹性层,该方法同样适用。对粘弹性层的研究,利用伯格斯模型给出了两个算例,首先研究泊松比随时间变化的情况,即在频域中泊松比随频率变化的情况;其次是研究泊松比为常数的情况,在这两种状况下分别得出沥青表面位移随时间的变化情况。
3.1 算例一
模型分为沥青层、地基层和底基层,其厚度分别为100 mm、300 mm 和15 000 mm。根据弯沉仪位移传感器的位置,分别计算了模型表面距载荷源中心位置0 mm、300 mm、600 mm、900 mm、1200 mm、1500 mm、1800 mm 的垂直方向位移,其受载荷的时程曲线如图8 所示,为50 ms的瞬态加载,其最大载荷为50 kN,载荷半径为150 mm。
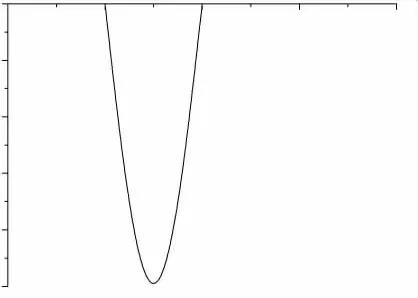
图8 载荷时程曲线图
图8 经傅里叶正变换得到的频谱图如图9 所示。从图9 可知,频率取0 Hz 到150 Hz 就能满足载荷随时间变化的要求。
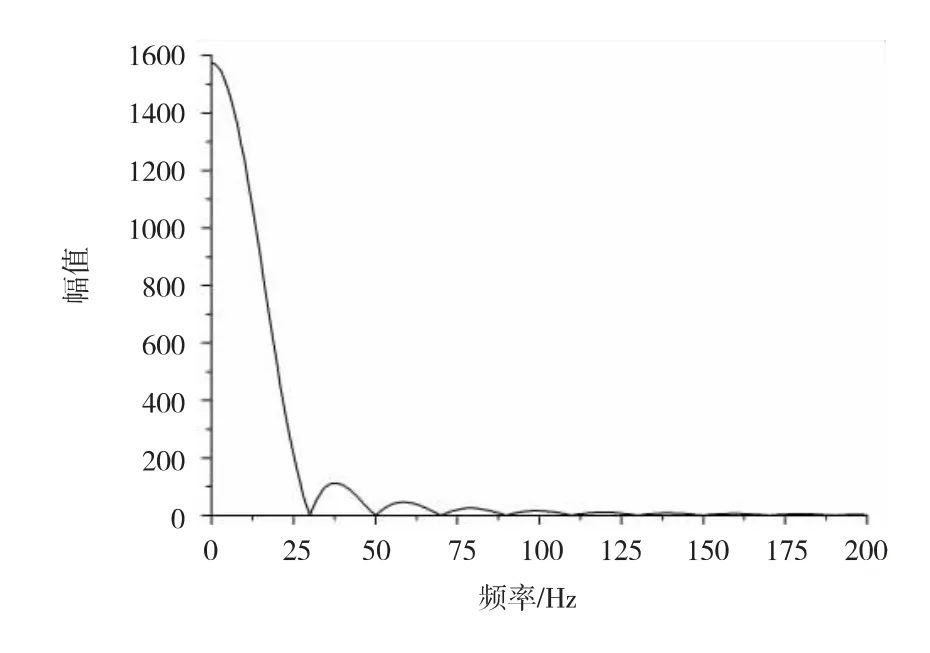
图9 载荷频谱图
F^m随m 的变化如图10 所示。从图10 可知,随m的增加,曲线幅值在不断的衰减,因此取M =1700 已能满足计算结果精确性的要求。为满足不同频率波传播,并使边界条件R 能充分满足所有振型情况,在算例中取R=25 m,这就能很好的计算出瞬态载荷作用与模型表面的位移。
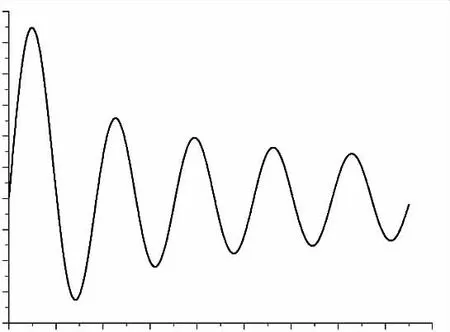
图10 傅里叶-贝塞尔系数分布图
在载荷时程曲线中( 图8) ,取时间周期T=1 s,载荷样本点数为4096,取样时间间隔Δt =0.000 244 s,因此取N=4096。模型结构分三层,分别模拟沥青、基层和底基层,均作为粘弹性材料来研究,其材料参数见表1。
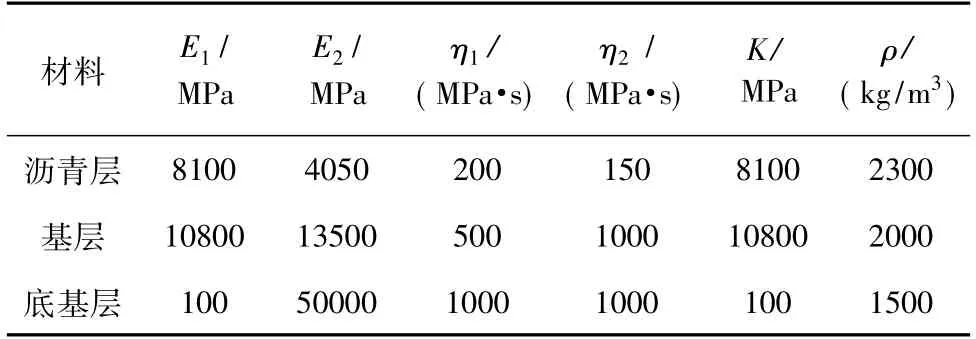
表1 粘弹性层参数
这里假设材料为弹性可压缩( σii= 3Kεii) 以及变形( Sij= 2u*( ω) eij) 的伯格斯模型。从表1 中沥青层的数据可得到的复剪切模量以及复泊松比随频率变化的情况,分别如图11 和图12 所示。
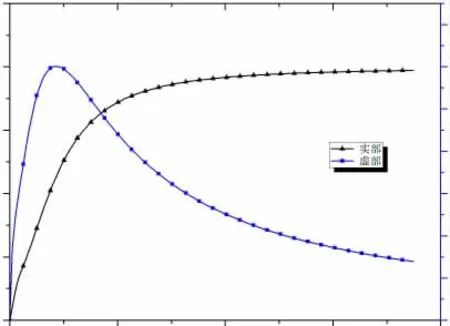
图11 复剪切模量的实部与虚部图
从图11 可知,当频率ω = 0 rad/s 时,其剪切模量为0,材料处于一种流体的状态。从图12 可知,伯格斯模型呈现出完全不可压缩的流体状态,但随着频率的增加,其可压缩性逐渐增加。
根据表1 中的参数数据,以及复剪切模量( 图11) 和泊松比的变化规律( 图12) ,通过程序代码可计算出模型表面距载荷源中心不同距离的垂直位移,如图13 所示。
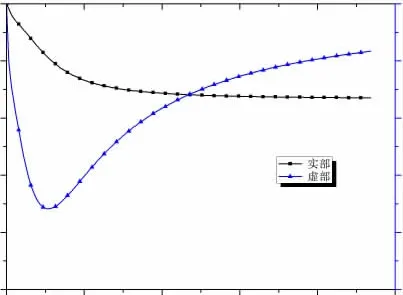
图12 复泊松比的实部与虚部图
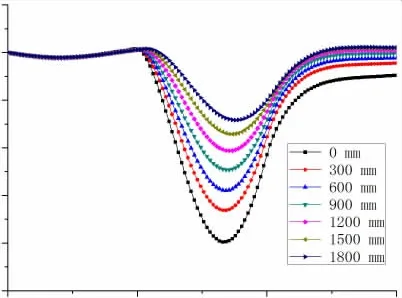
图13 模型表面垂直位移时程曲线图(泊松比变化)
不同位置最大位移曲线图如图14 所示,描述了在不同位置最大位移的趋势变化,由于轴对称性质,在距载荷源相同的位置其位移相等。
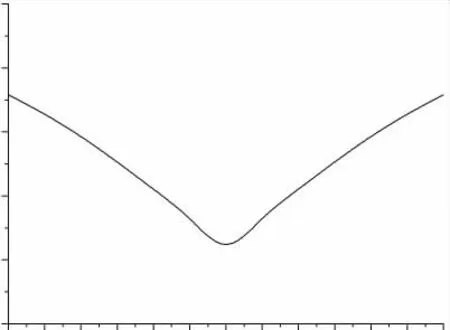
图14 不同位置最大位移曲线图(泊松比变化)
3.2 算例二
模型中其他参数不变,只将沥青层、地基层和底基层泊松比设为定值,都为0.45。通过程序计算得出距载荷源距离分别为0 mm、300 mm、600 mm、900 mm、1200 mm、1500 mm、1800 mm 的沥青表面垂直位移,其位移时程曲线和不同位置最大位移曲线分别如图15、图16 所示。
从图15 和16 可知,泊松比设为定值时,其位移时程和不同位置最大位移的变化趋势皆基本与泊松比变化时的趋势一致。
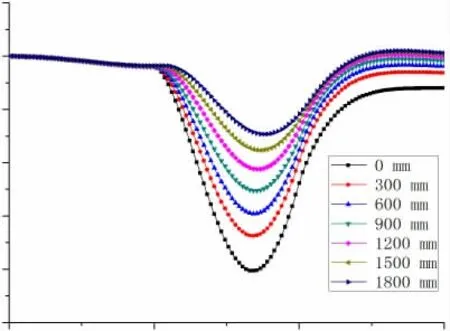
图15 模型表面垂直位移时程曲线图(泊松比为0.45)
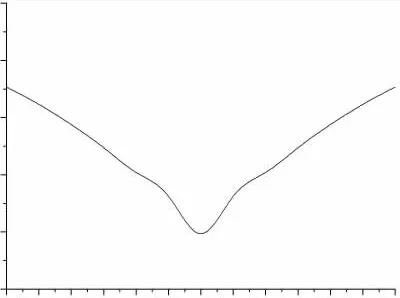
图16 不同位置最大位移曲线图(泊松比为0.45)
4 结束语
公路受到高温时,路面出现软化,使得其材料表现出粘弹性。本文以线弹性得到的谱元法理论为基础,对粘弹性层结构模型进行分析。为了便于计算,将模型结构简化为三层,分别模拟沥青层、地基层和底基层,并假定三层均表现为粘弹性,以泊松比随时间变化和泊松比不随时间变化为例,通过程序计算得出模型表面距离不同载荷源中心的垂直位移。
由算例一和算例二可知,随着距载荷源的距离越长,其同一时刻产生的位移不断减小,这符合瞬态力加载时产生的波在介质中传播不断衰减的特征; 同时,在距离载荷源不同位置产生的最大位移时刻不同,离载荷源越近,产生的最大位移时刻靠前,离载荷源越远,产生的最大位移时刻靠后,这符合瞬态动力学中的滞后现象。由轴对称性质可知,不同位置处的最大位移曲线变化趋势表明了动力学问题可以在某一时刻考虑成为静力学问题。通过使用波谱元法对粘弹性模型的位移计算的研究,可以更好的为路基层的参数识别提供可靠的理论和计算上的支撑。

