均值-方差准则下相依双险种最优再保险

蒋兰青

( 闽江师范高等专科学校初等教育系，福州 350108)

引 言

随着对保险破产概率研究的成熟和完善，越来越多的学者开始关注再保险对破产概率的影响，以及再保险设计如何达到最优，从而为原保险公司分散风险，扩大承保能力。已有不少文献研究过单一的成数或超额赔款再保险模型的破产概率，或者进一步讨论模型的最优自留额。王旭在文献［1］中讨论了离散时间比例再保险模型的破产概率，文献［2-3］均利用最小化破产概率讨论了最优的比例再保险问题，文献［4-7］利用期望效用函数最大化研究了最优化比例或超额损失再保险策略。而早在2002 年，Centeno M L 就在文献［8］中研究了成数超额赔款混合再保险模型，其中成数再保险保费按原始条款计算，而超额赔款再保费则依据期望值原则计算，并且假设理赔过程是一个复合Poisson 过程。李兴玉等在文献［9］中以经典破产理论为基础，将比例再保险和超额赔款再保险纳入考量，构造与风险态度有关的投资函数，再根据鞅方法得到与投资谨慎性有关的破产概率。

受前人的启发，本文建立成数和超额损失混合双险种再保险模型，并考虑两险种的理赔之间不是独立的，将Centeno M L 在文献［10］中的某种相依关系引入到模型中，建立了一类更符合实际的再保险模型。其次，考虑到原保险人利用再保险转嫁风险必然会减少其原有的期望收益，但是一个合理的再保险又可以通过增加安全性来降低风险，综合这两方面因素，保险人必须通过权衡收益和风险来得到最优策略。文献［11-14］均从不同角度研究了均值-方差准则下的最优再保险问题。文献［11］将保险公司比例再保险的收益和风险通过线性组合的方式，转化为单目标的最优决策模型，通过确定分出比例来使再保险的风险效用达到最大。根据该思想，最优再保险的决策问题就转化为再保险中相应参数的选取问题。本文运用均值-方差原理，即通过将总体风险最小和期望收益最大的双目标规划转化为单目标问题，得到了模型的相应参数，从而选取最优自留额。

1 预备知识与模型建立

定义1［15］计数过程{N( t) ，t ≥0} 称为参数为λ( λ ＞0) 的齐次Poisson 过程，如果:

(1) N(0) = 0;

(2) 过程有独立增量;

(3) 对任意的s，t ≥0;

定理1［16］关于齐次Poisson 过程的可加性。设M ={Mt，t ≥0} 和N = {Nt，t ≥0} 是强度分别为λ1和λ2的齐次Poisson 过程，并且两个过程相互独立，对于每一个ω ∈Ω 和任意的t ≥0，令:

Kt( ω) = Mt( ω) + Nt( ω)

则上式定义的过程K = {Kt，t ≥0} 称为过程M = {Mt，t ≥0} 和N = {Nt，t ≥0} 的叠加，且是服从强度为λ =λ1+ λ2的齐次Poisson 过程。

定理2［16］设{S( t) ，t ≥0} 是一个复合Poisson 过程，Poisson 过程{N( t) ，t ≥0} 的强度为λ，则:

(1) S( t) 有独立增量;

(2) 若E( Xi) ＜+ ∞，则E( S( t) ) = λtE( X1) ，Var( S( t) ) = λtE() 。

下面进行模型的建立。

设( Ω，F，P) 为一个完备的概率空间，本文考虑的所有随机变量都是定义在该概率空间上的。假设保险公司对两类险种采取不同的再保险策略，具体而言，对险种一的理赔选择自留比例为a 的成数再保险，对险种二的理赔选择自留额为M 的超额赔款再保险，建立如下的相依混合双险种再保险风险模型，保险公司的盈余过程与盈利过程分别为式(1) 和式(2) :

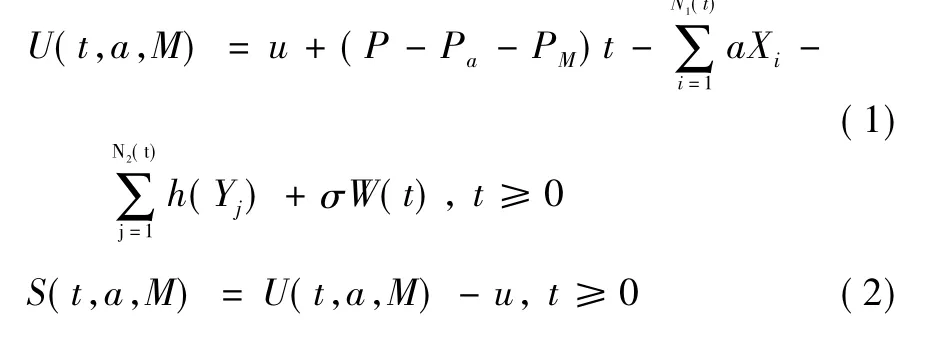
其中:

(1) u ≥0 为保险公司的初始资金，P 为单位时间的保费率。

(2) {Xi，i ≥1}，{Yj，j ≥1} 是取值于［0，∞) 上非负独立同分布的随机变量序列，分别表示险种一在第i次的理赔额及险种二在第j 次的理赔额，设其分布函数分别为F( x) ，G( y) ，均值分别为μ1，μ2，且对x ≤0 有F( x) = 0，对y ≤0 有G( y) = 0。

(3) N1( t) ，N2( t) 分别表示两类险种在t 时间内的理赔次数，令N1( t) = K1( t) + K( t) ，N2( t) = K2( t) +K( t) ，其中K1( t) ，K2( t) ，K( t) 分别服从参数为λ1，λ2，λ 的Poisson 分布且相互独立，这样两险种的各自理赔总额便通过K( t) 联系起来。由定理1 易知N1( t) ，N2( t) 是分别服从强度为λ1+λ，λ2+λ 的齐次Poisson 过程。

(4) h( Yj) = min{Yj，M} 表示险种二在第j 次的理赔额，Pa，PM分别为成数再保险和超额赔款再保险的单位时间再保费率，假设原保险公司与再保险公司都是按期望值原理收取保费，且原保险、成数再保险和超额赔款再保险的安全负载分别为θ，θ1，θ2( θ ≤θ1，θ ≤θ2) ，于是P = (1 + θ) ［( λ1+ λ) μ1+ ( λ2+ λ) μ2］，Pa=(1 + θ1) (1 － a) ( λ1+ λ) μ1，PM= (1 + θ2) ( λ2+λ) E［( Yj－ M)+］。

(5) {W( t) ，t ≥0} 为标准维纳过程，表示保险公司不确定的收益和支出，σ ＞0 为干扰因子。且假设{Xi，i ≥1}，{Yj，j ≥1}，{N1( t) ，t ≥0}，{N2( t) ，t ≥0}，{W( t) ，t ≥0} 之间相互独立。

定义2记Ta，M= inf{t| U( t，a，M) ＜0} 表示保险公司的破产时刻，若对所有t，均有U( t，a，M) ＞0，则Ta，M= ∞; 记ψ( u，a，M) = P( Ta，M＜∞| U(0) = u) ，∀u ≥0 表示最终破产概率。

2 均值方差下的最优再保险

引言中已指出均值－方差原理的思想，即通过将总体风险最小和期望收益最大的双目标规划转化为单目标问题，本节将利用该方法求解以下模型的最优自留额:

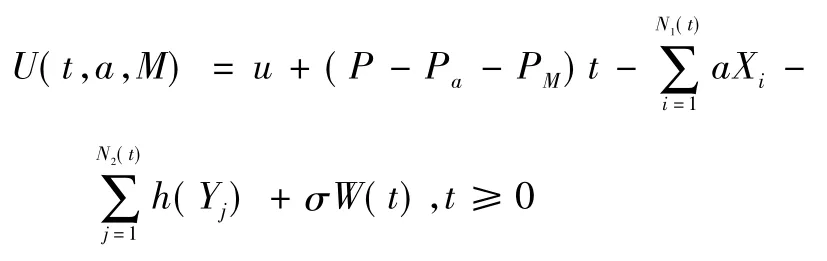
这里考虑在某一时间段内的理赔，记两类总理赔分别为:

由模型中的相关符号定义知，保险公司在该时间段内的期望收益为:

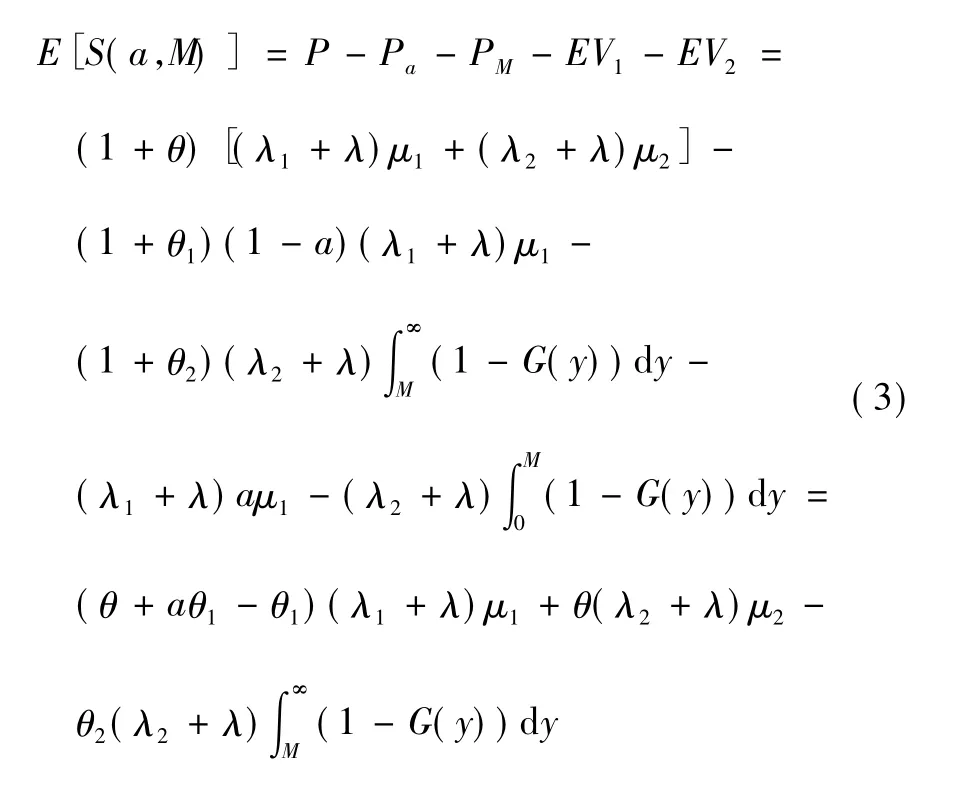
原自留总风险的方差为:

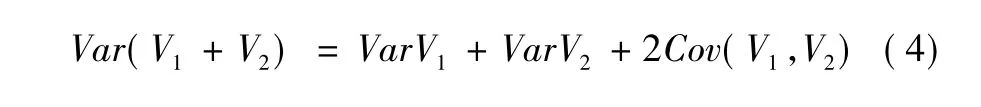
其中:

从而:

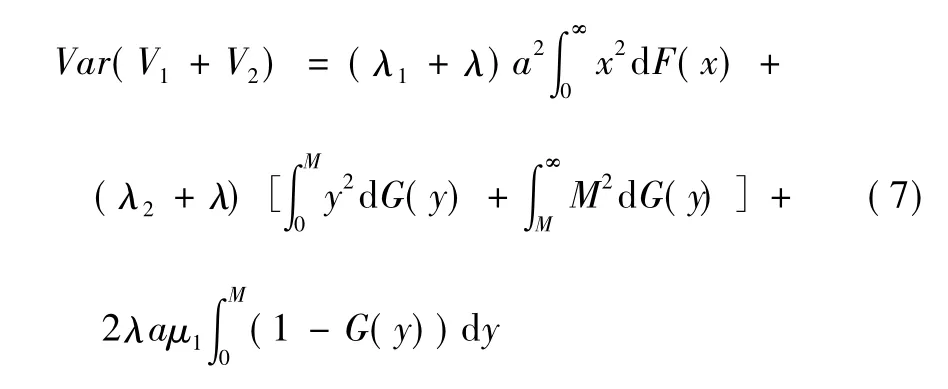
原保险公司是为了得到一个最优的再保险合同，即选取适当的a，M 后，能使总期望收益尽量的大，而同时总的风险尽量的小。然而这是一个非线性的双目标规划问题，两个目标相互冲突，当保险人厌恶风险时，其获得的收益就小，而当保险人追求收益时，其面临的风险就增大，因此无法得出最优解。但可以通过控制一个目标变量，而使另一个目标变量达到最优。本节就是在既定的期望收益下，使保险公司的总风险方差达到最小。

假设期望收益为k，可以利用Lagrange 乘数法来求上述问题的最优解，此时Lagrange 函数为:

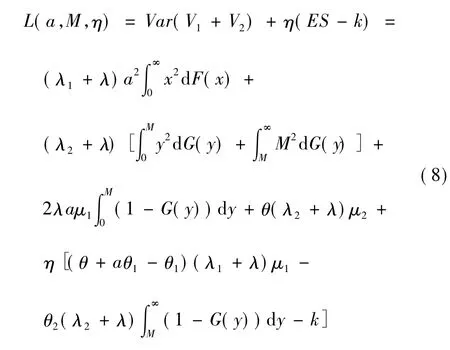
式(8) 分别对a，M，η 求偏导，并令其为0，得:

由式(9) － 式( 11) 组成的方程组的解即为所要的最优解。当理赔的分布函数确定时，代入上述方程组即可求得最优解。

3 应用举例

设两险种理赔额{Xi，i ≥1}，{Yj，j ≥1} 均服从参数为1 的指数分布，即F( x) = 1 － e－x，x ＞0; G( y) =1 － e－y，y ＞0，于是μ1= μ2= 1，且:

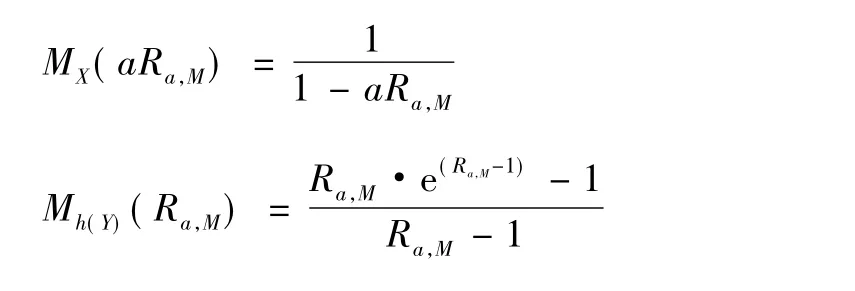
假设θ = 0.2，θ1= θ2，= 0.3，λ1= λ2= 1，σ =0.05，k = 0.6，根据这些数据并利用Matlab 计算得:成数再保险的最优自留比例a = 0.6075，超额赔款再保险的最优自留额M = 1.2939。