一种小数据量的通信信号符号速率估计方法

李啸天

(中国电子科技集团公司第五十四研究所，河北 石家庄050081)

0 引言

在非合作通信侦察背景下，符号速率等信息往往未知。为了正确进行解调，需要进行符号速率估计[1-4]。

传统的符号速率估计方法基于二次方谱[5-6]或者循环平稳特性[7-8]，在样本符号个数较多的条件下，信号的符号速率统计特性较为明显，该类方法具有较好的识别效果。然而，对于某些短时突发[9-11]或者高速跳频信号[12-15]，每一突发或者每一跳符号个数较少，甚至于只有几个符号，信号的统计特性不明显，无法正确进行识别。从通信侦察角度考虑，非合作方受限于地理位置等不利因素，往往也不能够获取足够长度的信号样本。针对此问题，学者们提出了基于过零检测的符号速率估计方法[16-17]，该方法利用调制信号的过零特征。以PSK信号为例，其基带信号为成型的极性信号，不同的符号间存在过零点，利用基带波形的过零间隔能够在符号个数较少时识别出符号速率。然而，基于过零检测的符号速率估计方法受噪声影响较为严重[18-21]，噪声会破坏信号的过零特性，导致该方法在低信噪比条件下识别性能较差。

本文提出一种基于判决反馈的符号速率估计方法。针对短时突发或高速跳频等符号个数较少的情况，该方法利用已知符号速率集，首先对接收信号的基带波形按照集合中的符号速率进行判决，根据判决结果生成方波信号与原始基带信号进行相关，若相关值大于事先确定的门限值，则认为当前符号速率为真实符号速率。仿真试验表明，该算法的信噪比性能明显优于过零检测方法。

1 信号模型

以恒包络PSK信号为例，其正交下变频之后的I路基带信号可表示为[22]：

(1)

式中，K为当前突发内符号个数，Ak= 1或-1为发送码元，g(t)为脉冲成形滤波器，Ts为符号周期，n(t)为高斯白噪声。设采样率为fs，则经过无失真采样后的数字基带信号为：

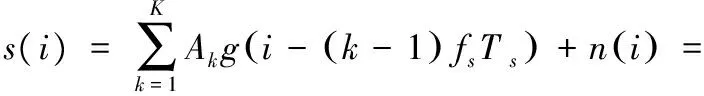
(2)

式中，N=fsTs为过采样率。在采样率已知的情况下，估计符号速率等价于估计过采样率N，即符号间隔。

为了保证信号频谱具有较好的滚降特性，成型滤波器一般设计为升余弦函数结构：

(3)

式中，0≤β≤1为滚降系数。不同β取值条件下成型滤波器时域波形如图1所示。

图1 成型滤波器时域波形

从图1中可以看出，对于不同β，成型滤波器时域波形具有如下3个特征。

特征1：g(i)为偶函数，即左右对称；

特征2：-N≤i≤0时，g(i)为单调递增函数，0≤i≤N时，g(i)为单调递减函数，且-N≤i≤N时，g(i)≥0；

特征3：g(i)大部分能量集中在主瓣范围(-N≤i≤N)内。

2 过零检测方法

当突发信号符号个数K较小时，基带码流更容易出现连0或连1现象，导致基带信号符号速率频率特征不明显，无法利用二次方谱或包络谱等传统方法识别符号速率。因此，目前实际工程应用中一般采用过零检测方法。

在不考虑噪声影响条件下，首先证明：对于2个相邻符号A0和A1，其判决最佳采样点分别为i= 0和i=N，则区间[0,N]内存在过零点的充分必要条件为A0≠A1，且过零点在i=N/2处。

证明：

首先证明充分性。设A0=1，A1= -1，可得：

s(i)=g(i)-g(i-N)。

(4)

根据特征1可得两符号交界处i=N/2时：

s(N/2)=g(N/2)-g(-N/2)=0，

(5)

A0=-1，A1= 1时可得相同结论，充分性证毕。

接下来证明必要性。根据特征1可得：

s(i)=A0g(i)+A1g(i-N)=

A0g(i)+A1g(N-i)。

(6)

由特征2可知对于0≤i≤N，g(i)≥0，g(N-i)≥0，则要使s(i)=0，必须满足A0A1<0，即A0≠A1。另外容易证明，对于0≤i≤N，A0g(i)与A1g(N-i)具有相同的单调性，因此s(i)也是单调递增或递减的，则在区间[0,N]内s(i)只能有一个过零点，即在i=N/2处。必要性证毕。

上述定理只考虑了区间[0,N]内的情况，原因是该区间是相邻两个符号的主瓣影响区间。该区间内除了相邻两个符号的主瓣，还有可能存在其他符号的旁瓣分量影响信号过零特性。根据特征3，暂不考虑其他符号旁瓣影响。

根据上述定理可以得出，不考虑噪声的情况下，基带信号的过零点必然是两个符号最佳采样点的中点，即两符号交界点，则基带符号的过零点间隔必然是符号周期的整倍数。根据此特征，可得基于过零检测的符号速率估计算法流程：

① 数据初始化：备选符号速率集合{R1,R2,R3,……,RM}内符号速率由低到高排列，M为符号速率个数；输入基带信号s(i)，其采样长度为L，采样率为fs。

② 分别计算各符号速率对应过采样率，即符号间隔：

Nm=fs·Rm,m=1,2,3,…,M。

(7)

③ 计算s(i)过零点：

PZ={ipz|s(ipz)·s(ipz-1)<0,i=2,3,…,L} 。

(8)

计算过零间隔：

PZS=diff(PZ)={S1,S2,S3,…,ST}，

(9)

式中，T为过零间隔个数。

④ 设m= 1。

⑤ 计算代价函数：

(10)

⑥ 如果Bias< 0.1×L，则Rm为符号速率估计值；否则m=m+ 1，返回步骤⑤。若m=M且仍不满足Bias< 0.1×L，则识别失败。

在实际通信系统中，为便于实现，备选符号速率往往会采用倍频的形式，即符号速率间是整倍数关系。这种情况会导致符号速率模糊问题，若识别出符号速率为Rm，真实符号速率有可能是Rm整倍数。在上述算法中，若符号速率集是整倍数关系，且对于第m个符号速率满足Bias< 0.1×L约束条件，则第m+1、m+2、……个符号速率必然仍满足约束条件，因此只能按符号速率由低到高遍历，取最低符号速率值为估计值。设真实符号速率为R，过零间隔N= 1/R，则不同传输码流条件下Bias计算结果如表1所示。

表1 传输码流与bias关系

传输码流过零间隔计算Bias所用符号速率Bias110011001101110111012N、2N2N、2N2N、N、N2N、N、N2N、N、NR/2RR/2R2R002N00

基带码流为1100，则符号速率为R的基带波形与符号速率为R/2的基带波形相同，按2种符号速率计算Bias均为0；若基带码流为1101，则按符号速率为R/2计算Bias为2N，可确定真实符号速率不等于R/2，按符号速率为R计算Bias为0，可正确识别符号速率，按符号速率为2R计算Bias仍为0，因此必须按照符号速率由低到高遍历。

若备选符号速率集均不存在整倍数关系，则不会产生符号速率模糊问题，上述算法步骤④、⑤、⑥可改为遍历M种符号速率计算代价函数Bias，取Bias最小值对应的符号速率为估计值，此时估计算法具有更高的可靠性。

3 判决反馈方法

从第2节所述算法可以看出，噪声会严重影响过零检测方法的性能。噪声的起伏将会使基带波形过零点发生较大偏移，导致符号速率估计错误。针对此问题，本文提出一种基于判决反馈的符号速率估计方法。该方法根据已知符号频率集，分别进行基带判决，并根据判决结果生成方波信号作为模板，与原始基带信号进行相关匹配，如匹配值大于预先设定的门限值，则认为当前符号速率为真实符号速率。基于判决反馈的符号速率估计算法流程如下：

① 数据初始化：备选符号速率集合{R1,R2,R3,……,RM}内符号速率由低到高排列，M为符号速率个数；输入基带信号s(i)，其采样长度为L，采样率fs；计算相关门限：

(11)

② 分别计算各符号速率对应过采样率，即符号间隔：

Nm=fs·Rm,m=1,2,3,…,M；

(12)

③ 设m= 1；

④ 将基带信号s(i)根据Nm进行极性判决：

(13)

⑤ 根据判决结果生成方波模板：

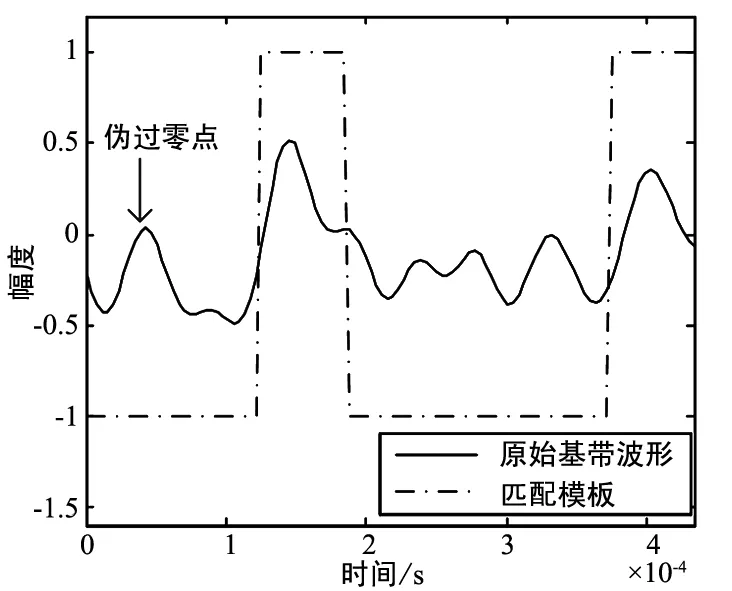
sm(i)=au, (u-1)Nm+1≤i

(14)

⑥ 计算基带信号s(i)与模板sm(i)的相关值：

(15)

⑦ 若Cm≥T，则Rm为符号速率估计值；否则m=m+ 1，返回步骤③；若m=M且仍不满足Cm≥T，则识别失败。

基于判决反馈的符号速率估计方法受符号速率倍数关系的影响，以及在非倍数符号速率条件下算法可做的改进，与过零检测相同，在此不多做赘述。相较于过零检测方法，该方法利用了基带信号的幅度信息，在一定程度上弱化了噪声对过零点的影响，因此性能优于过零检测方法。

基于判决反馈的符号速率估计方法在判决过程中需要定时同步，否则错误的模板会导致符号速率估计错误。针对此问题，提出以下2种解决思路：

① 短时突发信号同步技术[23-24]。在进行突发信号检测时，利用双滑动窗等能量检测方法，精确获得突发起始点作为第一个符号起始点。

② 过零检测与判决反馈联合的符号速率估计方法。若由于信噪比等原因，无法通过能量检测精确获取突发起始点，可结合过零检测与判决反馈方法，利用第一个过零点作为式(13)的判决起始点，前后同时判决生成基带模板。

4 仿真试验

本试验利用蒙特卡洛仿真验证判决反馈算法的识别正确率，试验参数如下：采样率1 024 kHz；突发时长500 μs；目标信号调制样式为BPSK，符号速率分别为16 ksps、32 ksps、64 ksps，则每一突发符号个数分别为8、16、32；蒙特卡洛仿真次数为2 000。

信噪比为5 dB、符号速率为16 ksps条件下，经过下变频及抽取滤波之后的基带原始波形与匹配模板如图2所示。从中可以看出，低信噪比条件下，随机出现的伪过零点会破坏原始基带信号仅在两符号交界点过零的特性，利用过零检测算法会导致符号速率估计错误。然而，考虑到噪声的随机抖动，伪过零点间信号幅度不会很大，因此不会影响判决正确性，利用判决结果生成的方波模板能够较好地重现波形幅度特征，与原始基带信号进行相关，能够得到较高的相关值，保证符号速率估计正确。

图2 原始基带波形与匹配模板

符号速率为32 ksps条件下，过零检测算法与判决反馈算法的识别正确率如图3所示。从中可以看出，判决反馈算法符号速率估计性能明显优于过零检测算法。在识别正确率大于80%区域，判决反馈算法信噪比性能优于过零检测算法6 dB以上。

不同符号速率条件下判决反馈算法的信噪比性能如图4所示。从中可以看出，信噪比高于5 dB时，识别正确率随着符号速率的提升而提升，原因是信噪比较高时基本可保证基带信号判决正确，此时生成的匹配模板正确，则符号速率越高，相关符号个数越多，性能越好；当信噪比低于5 dB时，识别正确率随着符号速率的提升而下降，原因是低信噪比条件下判决误码导致匹配模板生成错误，此时符号速率越高，过采样率越低，基于能量的判决性能越差。

图3 过零检测与判决反馈算法性能对比

图4 不同符号速率条件下判决反馈算法性能

5 结束语

本文针对样本符号个数较少条件下的符号速率估计方法进行研究。针对传统过零检测算法受噪声影响严重，伪过零点会恶化识别性能的问题，提出了一种基于判决反馈的符号速率估计方法。该方法利用基带判决生成匹配模板，与原始基带信号进行相关匹配，估计符号速率。仿真试验表明，识别正确率大于80%条件下，基于判决反馈的符号速率估计方法信噪比性能优于传统过零检测方法6 dB以上。本文提出的方法适用于短时突发、高速跳频等样本符号个数较少的目标信号非合作接收系统中，可以提升信号侦收性能与参数指标。

[1] 陈卫东.数字通信信号调制识别算法研究[D].西安: 西安电子科技大学,2001.

[2] Tang S,Yu Y.Fast Algorithm for Symbol Rate Estimation[J].IEICE Transactions on Communications,2005,88(4): 1649-1652.

[3] 刘维倩.数字调制信号符号速率的测量[J].国外电子测量技术,2013,32(8):31-33.

[4] 石明军,邓名桂,肖立民,等.一种新的数字调制信号符号率估计和同步算法[J].通信技术,2009,42(1):40-42,45.

[5] Yang W C,Yang X Q.Research on Symbol Rate Estimation Based on the Generalized Square Envelope Spectrum[C]∥2015 IEEE International Conference on Communication Problem-Solving,2015: 391-394.

[6] 袁本义,于宏毅,田鹏武.基于信号二次方谱相关特征的MPSK调制识别[J].信号处理,2011,27(4): 558-562.

[7] 金艳,姬红兵.基于循环自相关的PSK 信号码速率估计的噪声影响分析[J].电子与信息学报,2008,30(2):505-508.

[8] Soliman S S ,Hsue S Z.Signal Classification Using Statistical Moment[J].IEEE Transactions on Communications,1992,405: 908-916.

[9] 张浩.短时突发信号侦察技术研究[D].成都: 电子科技大学,2015.

[10] 杜谦.一种实用的MPSK/TDMA 突发信号盲解调方案[J].无线电工程,2016,46(3): 15-17,61.

[11] 廖明.短时突发PSK信号分析和盲解调技术研究[D].绵阳:中国工程物理研究院,2014.

[12] 刘延路,孙晨华,王赛宇.跳频卫星信号传输波形设计研究[J].无线电工程,2017,47(2): 28-31.

[13] 孙海祥,王晓亚.高速跳频信号解调算法研究[J].中国无线电,2008(7): 64-67.

[14] 王硕.基于FPGA的快跳频系统模块的设计与实现[D].哈尔滨:哈尔滨工业大学,2016.

[15] 魏来,龚晓峰.跳频信号参数估计的优化算法研究[J].计算机仿真,2016,33(6):223-227.

[16] Elgenedy M A,Elezabi A.Blind Symbol Rate Estimation Using Autocorrelation and Zero Crossing Detection[C]∥IEEE ICC 2013 Signal Processing for Communications Symposium,2013: 4750-4755.

[17] 芦跃.数字信号调制识别及参数估计研究[D].苏州: 苏州大学,2013.

[18] 郭建涛,王宏远.低信噪比下的跳频信号参数估计[J].计算机工程与应用,2010,46(27): 142-144.

[19] 栾海妍,江桦.基于小波变换的跳频信号跳速盲估计算法研究[J].通信技术,2007,40(7): 30-32.

[20] 茹乐,杜兴民,毕笃彦.STFT 与SOPC技术相结合实现高速跳频图案的识别与跟踪[J].电视技术,2005(1): 40-44.

[21] 金龙,詹磊，沈永健,等.PSK通信信号的干扰算法研究[J].电子信息对抗技术,2014(5):55-61.

[22] Proakis J G.Digital Communications(Fifth Edition)[M].New York: McGraw-Hill,2007.

[23] 王成.短波突发信号同步技术研究及DPS实现[D].郑州: 解放军信息工程大学,2010.

[24] 罗欢吉,夏高峰.一种突发通信信号检测及同步算法[J].航空电子技术,2015,46(4): 1-6.