自由面与最小抵抗线对爆破振动的影响分析

何 闯， 尹冬梅， 王海亮， 闫鸿浩

0 引言

掏槽爆破的槽腔为后续起爆的其他炮孔提供了第2自由面，后续起爆的其他炮孔自由面数目越多、最小抵抗线越小，受岩石夹制作用越小[1]。因此，需对后续起爆炮孔的单段最大起爆药量、炮孔间排距等爆破参数进行调整。目前，我国GB 6722—2014《爆破安全规程》[2]中规定的萨道夫斯基公式未考虑自由面与最小抵抗线对爆破振速的影响，导致后续起爆炮孔单段最大允许起爆药量的理论计算值偏离实际值，因此，亟需对已有理论进行补充。曹孝君[3]、向亮[4]和王仁涛等[5]通过现场监测发现，受自由面条件的影响，不同类型的炮孔爆破引起的振动效应差异较大，其中掏槽孔爆破振动效应最强烈； 刘清泉等[6]、汪传松等[7]、陈星明等[8]、梁雪松[9]和张建平[10]均指出，随着自由面个数的增多，爆破振动强度降低； 文献[11]和文献[12]均指出，有自由面时爆破产生的振动速度比离自由面较远的夹制爆破产生的振动速度小； 闫鸿浩等[13]指出，测点与振源的相互位置不同时，即使测点在等距离或等高程上，振速的大小也不同； 张南等[14]经现场试验发现爆破抛掷反方向产生的爆破地震波对周围结构危害相对较大； 池恩安等[15]发现自由面越充分，爆破振动的危害效应越低，越有利于结构的安全； 张成良等[16]通过在预裂缝内、外侧布置测点，经分析得到地震作用最强烈的地方是最小抵抗线的后方。由目前的研究成果可知，国内外学者侧重于研究自由面或最小抵抗线与爆破振速的关系，缺少对自由面、最小抵抗线和爆破振速三者综合关系的研究。掏槽爆破成腔后，后续起爆炮孔的自由面与最小抵抗线均发生变化。因此，有必要以工作面与槽腔作为自由面确定后续起爆炮孔的最小抵抗线及其方向，对爆破振动规律做进一步的研究。本文以青岛地铁2号线延安路站右线TBM始发导洞近接建筑物爆破施工为背景，通过地表测点同步监测，研究爆破振动、自由面和最小抵抗线三者之间的关系，以期为爆破方案提供一定的指导和参考。

1 工程概况

延安路站右线TBM始发导洞位于车站主体南侧、1号风道与车站主体交叉处，沿延安三路敷设，总长30.1 m。导洞主要位于中风化花岗岩和微风化花岗岩带，局部位于强风化花岗岩下亚带，围岩等级为Ⅳ～Ⅴ级，采用上下台阶施工。导洞上覆岩层厚度约为17 m，西南侧6.52 m为金狮大酒店(10层)，要求振速控制在1.5 cm/s以内； 东南侧28.1 m为172#居民楼，要求振速控制在0.5 cm/s以内。施工现场雷管采用第1系列毫秒延期导爆管雷管，炸药采用2号岩石乳化炸药，共布置4个测点，采用TC-4850测振仪监测测点振速。右线始发导洞与金狮大酒店、172#居民楼及测点的位置关系如图1所示。

2 试验爆破方案

因上台阶是爆破振动控制的重难点，本文只对上台阶进行研究，共采用3种爆破方案进行了试验。3种爆破方案的炮孔间距、炮孔个数、起爆网路、雷管段别等爆破参数相同，只对炮孔深度和单孔装药量进行调整。上台阶开挖断面宽7.8 m，高3.9 m，断面面积23.89 m2，分2次起爆。第1炮爆破掏槽区域A-Ⅰ和掏槽两侧区域A-Ⅱ，A-Ⅰ和A-Ⅱ之间用第20段雷管进行孔外延期； 第2炮爆破拱顶区域B。掏槽区域A-Ⅰ采用多级楔形掏槽。上台阶炮孔布置如图2所示。3种爆破方案的炮孔个数均为108。

3种爆破方案的上台阶掏槽布置如图3所示。方案1、2和3的爆破循环进尺分别为1.0、1.8、1.5 m，总装药量分别为30.2、44.7、37.9 kg。1)第1种方案： 第1级到第4级掏槽孔单孔装药量分别为0.2、0.4、0.4、0.3 kg，A-Ⅱ区域的辅助孔、周边孔及底板孔单孔装药量均为0.3 kg，B区域的辅助孔及周边孔单孔装药量均为0.2 kg； 2)第2种方案： 第1级到第4级掏槽孔单孔装药量分别为0.2、0.6、0.6、0.45 kg，A-Ⅱ区域的辅助孔、周边孔及底板孔单孔装药量均为0.45 kg，B区域的辅助孔及周边孔单孔装药量均为0.3 kg； 3)第3种方案： 第1级到第4级掏槽孔单孔装药量分别为0.2、0.5、0.5、0.4 kg，A-Ⅱ区域的辅助孔、周边孔及底板孔单孔装药量均为0.4 kg，B区域辅助孔及周边孔单孔装药量均为0.25 kg。

(a) 平面位置关系

图1右线始发导洞与金狮大酒店、172#居民楼及测点的位置关系(单位： m)

Fig. 1 Relationships among shield launching adit on right line, Jinshi Hotel, residential building #172 and monitoring points(unit： m)

3 爆破振动监测数据分析

在右线TBM始发导洞采用3种不同的爆破方案共进行了6个爆破循环试验，通过4台测振仪共获得16组爆破振动数据，从中选取10组有效的典型数据进行分析。

除尺寸标注外，阿拉伯数字均代表雷管段别。

图2上台阶炮孔布置(单位： mm)

Fig. 2 Layout of blasting holes on top heading(unit： mm)

(a) 方案1

(b) 方案2

(c) 方案3

3.1 爆破数据

利用爆破测振仪的配套软件Blasting Vibration Analysis分别提取上台阶不同爆破区域的最大爆破振速及其出现时间、出现位置、炮孔深度、自由面个数、最小抵抗线和爆心距等爆破参数。本文中最小抵抗线方向“左右”指的是最小抵抗线指向隧道两侧，首排(列)辅助孔指的是距离辅助孔爆破抛掷自由面最近一排(列)的辅助孔。掏槽区域A-Ⅰ、掏槽两侧区域A-Ⅱ和拱顶区域B的振动参数见表1。

表1 掏槽区域A-Ⅰ、掏槽两侧区域A-Ⅱ和拱顶区域B的振动参数

由表1可知：

1)掏槽区域A-Ⅰ、掏槽两侧区域A-Ⅱ和拱顶区域B的爆破振速峰值分别由第2级掏槽、首列辅助孔和首排辅助孔爆破产生。由分析可知，掏槽区域A-Ⅰ第2级掏槽孔、掏槽两侧区域A-Ⅱ首列辅助孔和拱顶区域B首排辅助孔起爆时，最小抵抗线在同区域内最大。由爆破理论可知，最小抵抗线越小，炸药爆炸能量释放得越快，会有越多的能量形成空气冲击波，较少的能量转化为爆破地震波，因此，振动强度越小。

2)爆心距、单段最大起爆药量等参数相同而自由面个数不同时，2个自由面的平均爆破振速峰值较1个自由面的小。

3)自由面个数相同、最小抵抗线方向不同时，产生的爆破振动峰值不同。

3.2 爆破振速衰减规律拟合与分析

采用最小二乘法对萨道夫斯基公式进行回归变换，代入表1中的相应数据，得到不同爆破区域的拟合回归方程。不同爆破区域的振速回归曲线如图4所示，回归参数见表2。

(a) 掏槽区域A-Ⅰ (b) 掏槽两侧区域A-Ⅱ (c) 拱顶区域B

图4 不同爆破区域的振速回归曲线

由表2可知：

1)自由面个数不同时，K和α的值也不同。自由面个数增多时，K值和α值均减小，且K值减小的速度快，α值减小的速度慢。

2)自由面个数相同时，由于最小抵抗线方向不同，K和α的值也不同。最小抵抗线方向为左右时，K值和α值较最小抵抗线方向向下的小，而单段最大允许起爆药量理论计算值较最小抵抗线方向向下的大。

4 右线TBM始发导洞爆破方案优化

4.1 优化方案

上台阶掏槽区域A-Ⅰ、掏槽两侧区域A-Ⅱ及拱顶区域B的场地系数和衰减系数各不相同，单段最大允许起爆药量理论值分别为2.1、5.3、2.8 kg。对上台阶优化如下：

1)上台阶爆破循环进尺优化为1.8 m，以提高施工效率。结合原爆破方案炮孔利用率，将掏槽孔最大深度优化为2.1 m，辅助孔深度优化为1.9 m。

2)掏槽区域A-Ⅰ是振动控制的关键区域。掏槽仍采用多级楔形掏槽，第1级掏槽孔炮孔长度增加至1.21 m，单孔装药量调整为0.3 kg，可以为第2级掏槽创造更大的槽腔体积，减小第2级掏槽产生的爆破振速。考虑到掏槽两侧区域A-Ⅱ的最大爆破振速由首列辅助孔产生，增设第5级掏槽，减小首列辅助孔的最小抵抗线。

3)槽腔形成过程中，只有1个自由面，故控制掏槽区域A-Ⅰ第1级掏槽、第2级掏槽和第3级掏槽的单段最大起爆药量分别为0.6、1.2、1.2 kg； 槽腔形成后，后续起爆的第4级、第5级掏槽孔有2个自由面，变为6孔1段(即6个炮孔使用同一段位的雷管)，单孔装药量调整为0.45 kg，单段最大起爆药量增大至2.7 kg。

4)掏槽两侧区域A-Ⅱ爆破振动易受控制，故减少其比钻孔数，并将辅助孔减少至2排。

5)拱顶区域B爆破时，存在2个自由面，故减少其比钻孔数，辅助孔间排距变为0.9～1.1 m。由于拱顶区域B辅助孔最小抵抗线方向竖直向下，爆破振动较掏槽两侧区域A-Ⅱ难控制，故调整拱顶区域单段最大起爆药量为1.8 kg，其中辅助孔单孔装药量为0.45 kg，周边孔单孔装药量为0.3 kg。

优化后上台阶炮孔布置如图5所示，掏槽孔布置如图6所示，爆破参数见表3。此时雷管段位充足，没必要进行分次爆破，故上台阶变为一次起爆。

4.2 优化效果

使用优化后的爆破方案进行8个循环的爆破施工，取得了显著的经济技术效果。优化后C2测点典型爆破振动曲线如图7所示，试验方案2与优化后爆破方案的经济技术参数对比见表4。

图5 优化后上台阶炮孔布置(单位： mm)

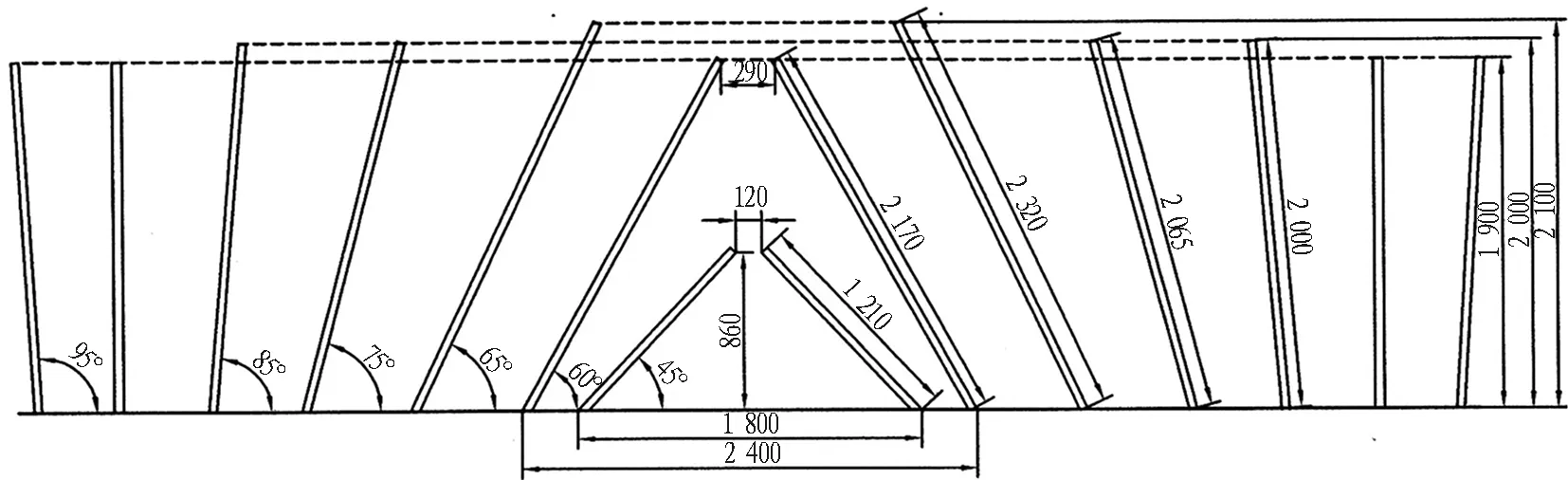
图6 优化后掏槽孔布置(单位： mm)

炮次炮孔名称雷管段别炮眼数炮孔深度/m单孔装药量/kg单段最大起爆药量/kgA第1级掏槽1、3、460．850．300．60第2级掏槽5～9101．900．601．20第3级掏槽10～1382．100．601．20第4级掏槽14～1582．000．451．80第5级掏槽16～1781．900．452．70辅助孔14～17141．900．451．80周边孔17～20201．900．301．80底眼孔13、14、18、1991．900．451．35合计833．6

下、上台阶一次起爆，1.2 s之前为下台阶爆破振动曲线。

图7优化后C2测点典型爆破振动曲线

Fig. 7 Typical blasting vibration curves of monitoring point C2 after optimization

表4 试验方案2与优化后爆破方案的技术经济参数对比

5 结论与建议

本文以青岛地铁2号线延安路站右线TBM始发导洞近接建筑物爆破施工为背景，对爆破振动与自由面、最小抵抗线的关系进行了研究，并对原爆破方案进行了优化。得出的主要结论与建议如下：

1) 爆破振动受自由面与最小抵抗线的共同影响。在爆心距、单段最大起爆药量相同而自由面数量不同时，自由面数量越多，位于隧道斜上方的质点振动强度越小； 自由面数量相同而最小抵抗线方向不同时，质点振动强度也不同。质点振动强度与最小抵抗线的大小也有一定的关系，相同条件下，质点振动强度随最小抵抗线的增大而增大。

2) 自由面个数不同时，场地系数K和衰减系数α也不同。随着自由面数量的增多，K值和α值均减小，且K值减小的速度快，α值减小的速度慢；自由面数量相同而最小抵抗线方向不同时，K值和α值也不同。不同爆破区域的K值和α值不同，使得不同爆破区域的单段最大允许起爆药量也不同。因此，在爆破设计时，应根据不同爆破区域的K值和α值分别核算单段最大允许起爆药量。

本文回归拟合了不同自由面个数和不同最小抵抗线方向条件下的场地系数K和衰减系数α，但未对最小抵抗线方向相同而大小不同时的场地系数K和衰减系数α进行回归拟合，只对爆破振动与最小抵抗线的关系做了理论性分析。后期工作可进一步研究最小抵抗线与爆破振动的关系，为优化爆破设计提供参考。

[1] 何闯, 王海亮. 针对消除落石危害的爆破参数优化研究[J]. 山东科技大学学报(自然科学版), 2016(2): 79.

HE Chuang,WANG Hailiang. Research on blasting parameter optimization to eliminate rockfall hazards[J]. Journal of Shandong University of Science and Technology(Natural Science), 2016(2): 79.

[2] 爆破安全规程: GB 6722—2014[S]. 北京: 中国标准出版社， 2015.

Safety regulations for blasting：GB 6722—2014[S]. Beijing: China Standard Press， 2015.

[3] 曹孝君. 浅埋隧道爆破的地表震动效应研究[D]. 成都: 西南交通大学， 2006.

CAO Xiaojun. Study of vibration effects of ground resulted from blasting in shallow tunnel[D]. Chengdu: Southwest Jiaotong University， 2006.

[4] 向亮. 城市浅埋硬岩大跨隧道开挖爆破振动监控研究[D]. 成都: 西南交通大学， 2009.

XIANG Liang. Monitoring study of blasting vibration of large-span shallow overburden hard rock tunnel in urban area[D]. Chengdu: Southwest Jiaotong University, 2009.

[5] 王仁涛, 王成虎, 宋凯. 青岛地铁超浅埋段爆破振动监测数据特征研究[J]. 中国安全生产科学技术, 2015, 11(12): 72.

WANG Rentao, WANG Chenghu, SONG Kai. Study of characteristics of monitoring data for blasting vibration in the ultra-shallow buried section of Qingdao Metro[J]. Journal of Safety Science and Technology, 2015, 11(12): 72.

[6] 刘清泉, 李玉民. 城市地下工程的减震爆破技术[J]. 煤炭科学技术, 1991(10): 11.

LIU Qingquan, LI Yumin. Vibration reduction blasting technology for urban underground engineering[J]. Coal Science and Technology, 1991(10): 11.

[7] 汪传松, 彭辉. 双自由面台阶爆破最小理论药包量的计算[J]. 武汉水利电力大学(宜昌)学报, 1999, 21 (2): 114.

WANG Chuansong, PENG Hui. A theoretic formula about the minimum charge quantity needed for two freedom surfaces bench blasting[J]. Journal of University of Hydraulic & Electric Engineering(Yichang), 1999, 21 (2): 114.

[8] 陈星明, 肖正学, 蒲传金. 自由面对爆破地震强度影响的试验研究[J]. 爆破, 2009, 26(4): 38.

CHEN Xingming, XIAO Zhengxue,PU Chuanjin. Experimental study of influence of blasting earthquake strength on free faces[J]. Blasting, 2009, 26(4): 38.

[9] 梁雪松. 自由面对爆破振动的影响研究[D]. 沈阳: 东北大学, 2013.

LIANG Xuesong. The effects of free surface on blast vibration[D]. Shenyang: Northeastern University, 2013.

[10] 张建平. 自由面数量对爆破振动规律影响实验研究[J]. 现代矿业, 2009(7): 46.

ZHANG Jianping. Experimental research on effects of free surface quantity on blasting vibration laws[J]. Modern Mining, 2009(7): 46.

[11] 熊代余, 顾毅成. 岩石爆破理论与技术新进展[M]. 北京: 冶金工业出版社, 2002.

XIONG Daiyu, GU Yicheng. New progress in theory and technology of rock blasting[M]. Beijing: Metallurgical Industry Press, 2002.

[12] SINGH P K . Blast vibration damage to underground coal mines from adjacent open pit blasting[J]. International Journal of Rock Mechanics & Mining Sciences, 2003, 20(2): 959.

[13] 闫鸿浩, 王小红. 城市浅埋隧道爆破原理及设计[M]. 北京: 中国建筑工业出版社, 2013.

YAN Honghao, WANG Xiaohong. Blasting principle and design of shallow-buried tunnel in urban area[M]. Beijing: China Architecture & Building Press, 2013.

[14] 张南, 方向, 范磊, 等. 微差爆破中起爆顺序对爆破振动的影响分析[J]. 爆破器材, 2013(1): 39.

ZHANG Nan, FANG Xiang, FAN Lei, et al. The influence of initiation sequences on blasting vibration in millisecond blasting[J]. Explosive Materials, 2013(1): 39.

[15] 池恩安, 赵明生, 梁开水, 等. 自由面数量对爆破地震波时频特性影响分析[J]. 爆破, 2013, 30(2): 16.

CHI En′an, ZHAO Mingsheng, LIANG Kaishui, et al. Influence of number of free surface on time-frequency characteristics of blasting seismic wave[J]. Blasting, 2013, 30(2): 16.

[16] 张成良, 梁开水, 唐海. 预裂爆破减振作用效果分析[J]. 爆破, 2003, 20(2): 17.

ZHANG Chengliang, LIANG Kaishui, TANG Hai. Analysis of effect of shock-absorption on presplit blasting[J]. Blasting, 2003, 20(2): 17.