基于车流量的智能交通信号优化控制研究
邱建东 解小平 汤旻安 佘 飞
1(兰州交通大学机电工程学院 甘肃 兰州 730070) 2(兰州交通大学新能源与动力工程学院 甘肃 兰州 730070)
0 引 言
随着汽车工业的发展和城市化进程的加速,我国城市常住人口和汽车数量呈现出了爆炸性增长的局面,交通拥堵问题日益严峻。特别是在交通高峰时段,一些城市交通路网甚至会出现局部瘫痪的现象,严重的影响了城市生活的质量,制约城市发展。各大城市在努力扩大交通设施建设的同时也在积极研究如何通过合理控制交通流,提高现有路网的利用率来缓解交通拥堵。城市道路呈现网状结构,十字路口多、通行效率低,加强十字路口交通管控是减少交通拥堵的关键环节,对缓解城市交通拥堵有着极其重要的现实意义。因此,城市交通信号灯的优化控制已经成为城市智能交通研究的重要课题之一[1-5]。而目前城市交通灯的控制主要还是固定配时控制,即根据统计到的各路口历史车流量数据而分配的相对比较合理的固定配时方案。固定配时方案存在灵活性差,不能根据路网的实际车流量进行动态调节等缺点,一定程度上造成了道路资源的浪费。
随着智能交通技术的发展,一些学者对交通信号灯的优化控制也做了许多研究。卫星等提出了基于遗传算法的交通灯自适应控制策略[6];Zhang等提出并建模求解了独立路口绿灯持续时间的动态范围优化设置问题[7];但这些方法都是基于单一路口的交通灯控制,并且需要经过多次迭代才能确定最优配时,在线控制效果较差。Dai[8]等提出了基于机器学习的自适应交通灯控制模型;张国刚研究了城市双交叉口交通信号协调模糊控制与优化算法[9];但随着交通网络的增大,模型建立和求解都比较困难,很难高效地应用与实际交通网络中[10]。针对目前智能交通信号灯控制方法的不足,根据相邻交叉路口车流量具有相关性[11]的特点,本文提出一种基于车流量的智能交通灯优化控制方法。建立了基于门限服务策略的交通灯轮询控制模型,利用马尔科夫链和概率母函数分析了交叉口车辆平均排队长度和信号灯配时方案,并且计算复杂度不会随着交通网络的增大而增加,简单高效地实现了智能交通系统的分布式控制。通过仿真实验验证了该控制方法的正确性和有效性,能够极大地缓解城市交叉路口的交通拥堵情况。
1 交叉路口交通网络模型的建立与分析
1.1 交叉路口交通网络模型的建立
在城市交通控制研究中,中心路口的控制是首要考虑的问题,而与中心路口相邻路口的车流量直接决定了中心路口的交通情况[12],本文以中心路口O为研究对象,建立的交叉路口交通网络模型如图1所示。
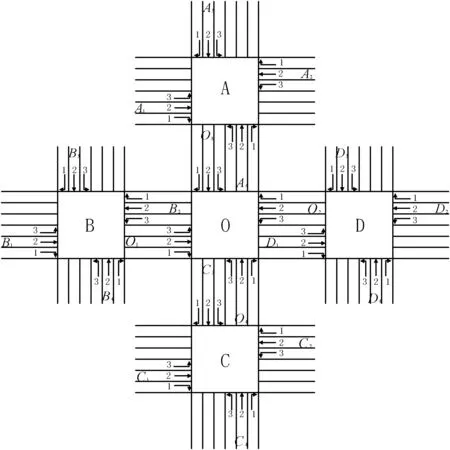
图1 交叉路口模型
如图1所示,设与中心路口相邻的有4个交叉路口,分别记为A、B、C和D,为了建模方便,假设交叉口之间的道路均为双向6车道,在到达中心路口前,在右转车道的车辆只能右拐弯,中间车道的车辆只能直行,左转车道的车辆只能左拐弯,为了统计车流量,在每个交叉口的上游和下游分别安装有车流量检测器。每个交叉口交通灯都采用四相位控制,相位图如图2所示。
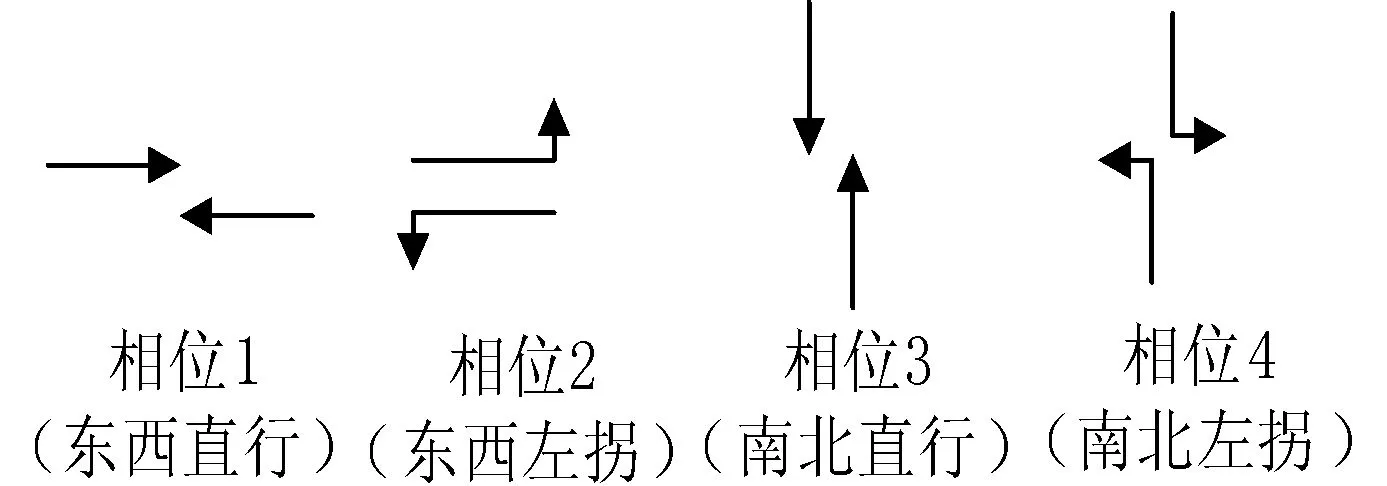
图2 交通灯四相位图
1.2 中心交叉口车流量控制模型
如图1所示,中心交叉路口与交叉路口A、B、C、D相邻,设在t时间内,从交叉口K驶向中心交叉口O的车辆数用Qko表示,从交叉口K的Kb方向M车道驶向中心路口O的车辆数用Qk-b-m(t)来表示,其中K为A、B、C、D,b为1、2、3、4,M为1、2、3。
QAO=t1QA-1-1(t)+t2QA-3-2(t)+t3QA-2-3(t)
(1)
QBO=t1QB-4-1(t)+t2QB-1-2(t)+t3QB-3-3(t)
(2)
QCO=t1QC-2-1(t)+t2QC-4-2(t)+t3QC-1-3(t)
(3)
QDO=t1QD-3-1(t)+t2QD-2-2(t)+t3QD-4-3(t)
(4)

QO=QAO+QBO+QCO+QDO
(5)
由式(5)可以看出,QO表示在t时间内从相邻交叉口驶向中心交叉口O的车流量之和,QO越大表示在下一时段交叉口O的交通流量压力越大。
如果要控制从交叉口K驶向中心交叉口O的车流量,只要调整交叉口K通往交叉口O方向的绿灯时间即可。设交叉口K通往交叉口O方向的绿灯时间为Tko,则此方向的车流量变化方程为:
(6)
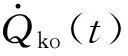
如果把与中心交叉口O相邻的所有路口都考虑在内,则中心交叉口O的车流量变化方程为:
(7)
由式(7)可以看出,只要调整各路口通往交叉口O的绿灯时间Tko就可以控制交叉口O的车流量。这也充分体现了交通路网中任何一个交叉路口的车流量均与相邻交叉路口有着很强的相关性。下面利用轮询控制模型来分析交叉口车辆平均排队长度和交通灯配时方案。
2 智能交通交叉口信号灯控制模型
2.1 交叉口信号灯轮询控制模型
轮询系统理论是排队论中多队列顾客共享服务资源的理论,由于其具有公平性、灵活性、高效性和实用性等特点,轮询理论在通信网络系统、物流系统和交通控制等领域得到了广泛的应用[13]。轮询系统的基本模型可以描述为,一个服务器按照某种服务规则依次对每一个队列进行服务,服务完最后一个队列再返回第一个队列,这样就实现了N个队列按照一定的服务规则共享一个或多个资源。在城市交叉路口的信号控制中,不同相位的排队车辆可以看成是不同队列,交通信号灯可以看作是轮流给不同相位的车辆提供服务使其获得通行权的服务器,交叉口内的道路空间即为公共资源。因此,轮询系统的理论研究结果可用于城市交叉口信号灯的配时优化分析与设计,4相位的交通灯可以看作是一个由4个队列和1个服务器组成的轮询控制系统,控制模型如图3所示。
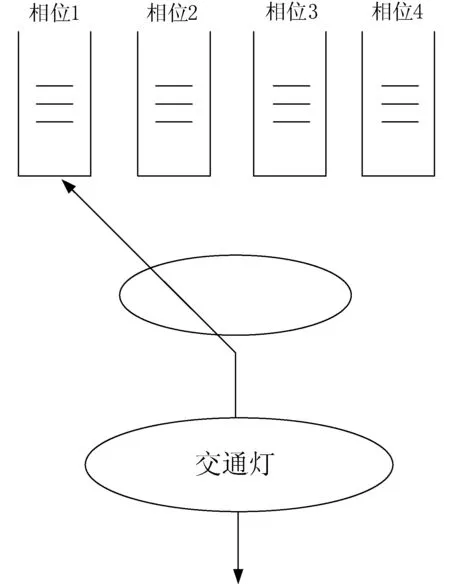
图3 交通灯轮询控制基本模型
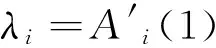
2.2 轮询控制模型的门限服务策略
轮询控制模型的典型服务策略包括完全服务、限定服务和门限服务[14]。其中限定服务的公平性较好,但平均等待时间较长;完全服务系统平均等待时间最短,但公平性较差;为了兼顾平均等待时长和不同相位之间的公平性,本文采取综合服务性能较好的门限服务策略来研究分析交叉口信号灯的优化配时问题。即根据各个相位的车流量对城市交叉口信号灯的配时进行动态调整,门限服务策略控制交通信号灯按照以下规则进行切换:
(1) 各相位车辆在通过路口时都必须遵循门限轮询服务规则,即一次绿灯服务时间需持续到上一周期内到达的对应相位排队等待的车辆(不超出设定的上限值L)全部通过才能切换,此绿灯服务时间内到达的车辆需等到下一周期绿灯时才能通行;
(2) 为了避免某一相位车辆排队过长而导致交通拥堵同时兼顾各相位之间的公平性,当某一相位的排队车辆数大于L时,每次绿灯服务时间内通过车辆L后进行相位切换。
2.3 交叉口交通灯动态配时分析
从前文对轮询控制系统的分析可知,交通灯的门限服务轮询控制系统主要包括以下三个独立的过程,即队列中对员(不同相位车辆)的到达过程、服务器(交通灯)对队员的服务过程(某一相位车辆获得通行权)和队列(不同相位)间的转换过程。为此,以下采用随机过程理论来分析交通灯的动态配时问题。
假设中心交叉口O的第l相位在tn时刻为绿灯,当在tn时刻之前到达的车辆全部通过后再经过一个黄灯时间,第l+1相位变为绿灯,在tn时刻第l相位排队等待通过中心交叉口的车辆用随机变量Qol(n)来表示,则具有N个相位的中心交叉口在tn时刻车辆排队状态的变量可表示为[Qo1(n),Qo2(n),…,Qoi(n),…,QoN(n)]。此时系统状态变量的概率分布为P[Qol(n)=xl;l=1,2,…,N],概率分布函数为πl(x1,x2,…,xl,…,xN);在tn+1时刻车辆的排队状态变量可表示为[Qo1(n+1),Qo2(n+1),…,Qoi(n+1),…,QoN(n+1)],此时系统的状态变量概率分布为P[Qol(n+1)=yl;l=1,2,…,N],概率分布函数为πl(y1,y2,…,yl,…,yN)。
在上述交叉口交通控制系统中,tn+1时刻的系统状态变量只与tn时刻的系统状态有关,是一个无后效性的马尔科夫(Markov)过程,因此在交通灯绿灯从i相位转换至i+1相位时,即在tn+1时刻各相位车辆的排队数量可以表示为:
(8)
式中:vi(n)表示i相位的绿灯时长;ui(n)表示黄灯时长;ηj(vi)表示在vi(n)期间到的j相位的车辆数;μj(ui)表示在ui(n)期间到达j相位的车辆数。
(9)
概率母函数为:
Gi(z1,…,zl,…,zN)=
(l=1,2,…,N)
(10)
在tn+1时刻,由式(8)可知各相位排队车辆数量的概率母函数为:
(11)
其中Al(□),Bl(□),和Rl(□)的含义如前文中所述。
定义在tn时刻当i相位的绿灯亮起时,第j(j≠i)相位车辆的排队数量为gi(j),由式(8)可知,相位j(j≠i)中车辆的排队数量为在tn时刻j相位中已有的排队车辆加上在i相位绿灯和黄灯时间内到达的车辆,根据门限服务策略和随机变量概率母函数的性质对其所对应的概率母函数求一阶偏导可得:
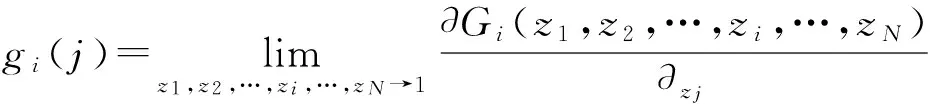
(12)
定义gi(i)为当i相位交通灯变为绿灯时该相位排队等待通过的车辆数,将式(8)代入式(11)并将计算结果求一阶偏导化简得到在该轮询模型控制下,交叉口某一相位的车辆平均排队长度为:
(13)
定义T为交通灯的配时周期,即交通灯按照门限服务策略对N个相位依次服务一遍的时间,由各相位绿灯通行时间和黄灯等待时间之和所组成[16]。根据轮询控制模型中的门限服务策略可知,相位i中在该交通灯配时周期内到达的车辆都要等待到下一次绿灯才能通过,因此,根据平均循环周期和车辆排队长度的关系可得交通灯配时周期为:
(14)
根据门限服务策略可知,在一个交通灯配时周期内相位i的绿灯时长为:
Ti=βiargmin(gi(i),Lth)
(15)
3 仿真实验
为了验证上述理论分析的正确性和优化控制策略的有效性,本文根据兰州市安宁区兴安路—万新北路交叉口的实际交通情况进行实例仿真,统计连续两周工作日的交叉口高峰期交通流量的平均值如表1所示。
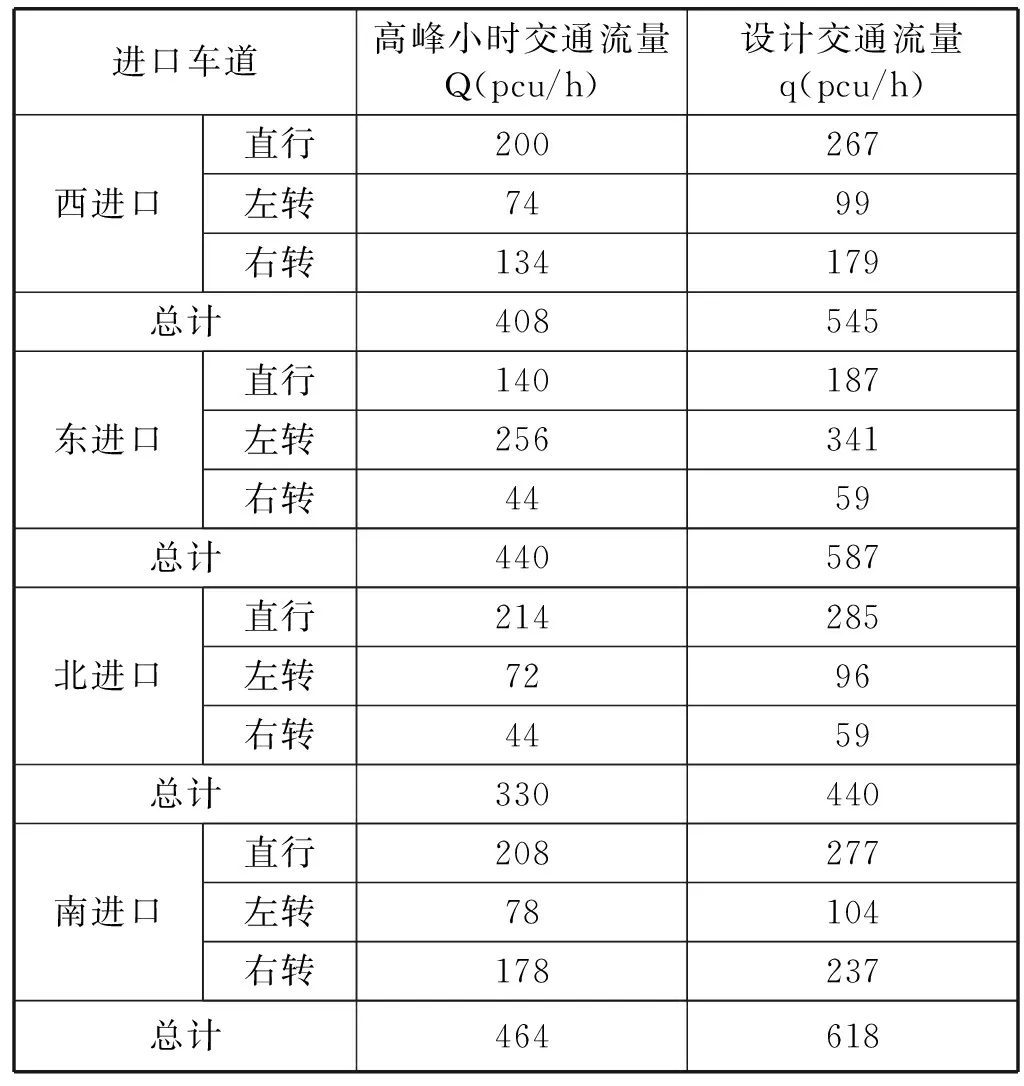
表1 高峰时段交通流量统计
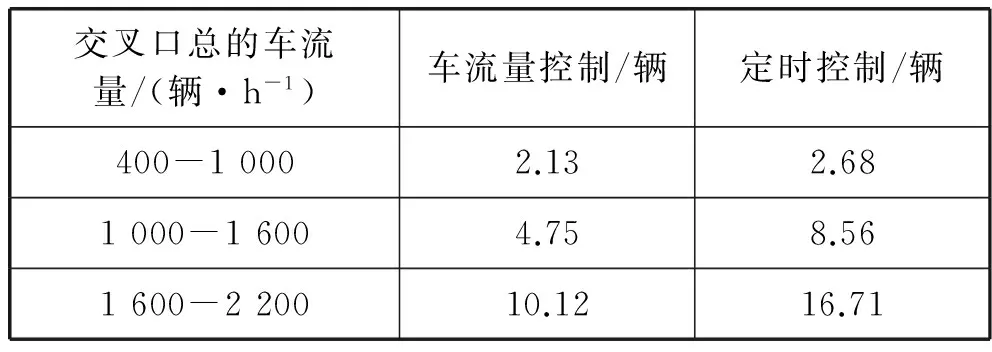
从表中数据可以发现,该交叉口各方向的总车流量均小于设计时的最大交通流量,但在统计数据的高峰时段各方向都出现了不同程度的交通拥堵现象,这说明该路口交通灯现有固定配时方法已经不能满足现有交通需求,交通路网无法得到最大效率的利用。为此,本文根据兴安路—万新北路交叉口的实际交通路网和采集到的交通流量,利用微观交通仿真软件VISSIM建立仿真模型,以车辆通过交叉口的平均延误和车辆平均排队长度为评价指标,从交叉口车流量400辆/h到饱到车流量2 200辆/h,分别对基于车流量的信号控制方法和固定配时信号控制方法进行仿真,仿真10个周期,两种控制方法的仿真结果对比如图4和表2所示。
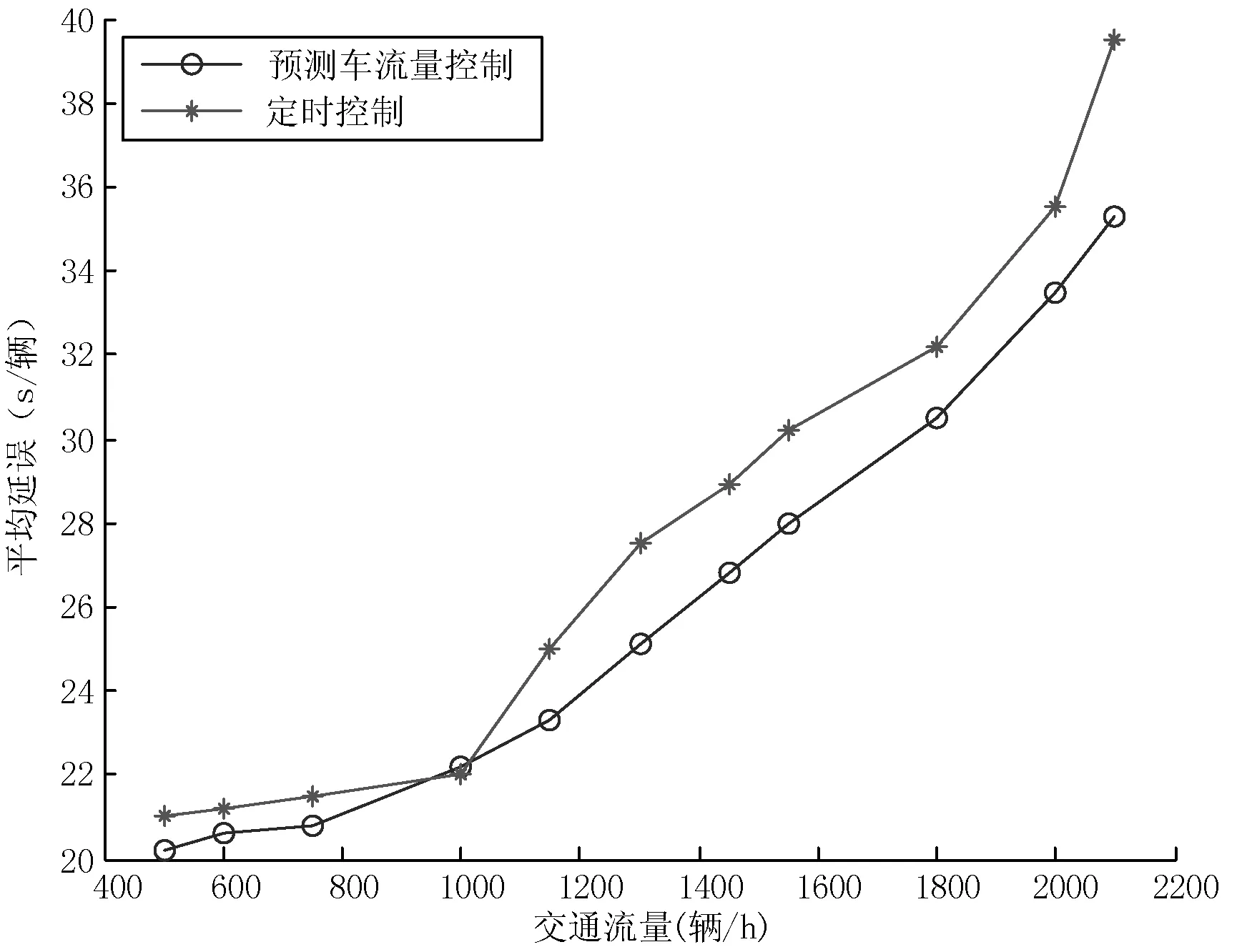
图4 不同交通状态下车辆平均延误
交叉口总的车流量/(辆·h-1)车流量控制/辆定时控制/辆400-10002.132.681000-16004.758.561600-220010.1216.71
从图4和表2可以看出,在车流量较小时,基于车流量的交通控制方法略优于定时控制方式,在车流量等于1 000辆/h时,两种控制方式下的车辆平均延误几乎相等。但随着车流量的增加,基于车流量的交通控制方式远远优于定时控制,使得车辆平均延误时间减少10.92%,在车流量接近饱和车流量时,更是将车辆平均排队长度由16.71辆减少到10.12辆。因此,基于车流量的智能交通信号控制方法比传统的定时信号控制方法能更加合理的控制交叉口的交通,在车流量相等的情况下能有效地降低车辆通过交叉路口时的平均延误时长和排队长度,提高通行效率。
4 结 语
本文提出了一种基于车流量的城市智能交通信号控制方法。根据相邻交叉路口车流量具有相关性的特点,提出一种基于车流量的智能交通信号控制方法,建立基于门限服务策略的交通灯轮询控制模型,利用马尔科夫链和概率母函数分析了交叉口车辆平均排队长度和信号灯配时方案,并根据实际交通情况进行仿真实验。结果表明,基于车流量的智能交通信号控制方法比传统的定时控制方法更加合理,能有效地降低车辆通过交叉路口时的平均延误时长和排队长度,达到了缓解城市交通拥堵,提高城市交叉路口车辆通行效率的目的。
[1] 杨照峰,张睿哲.实时自适应交通信号倒计时显示控制方法[J].计算机系统应用,2014,23(8):101-104.
[2] 刘脐锺,李兵.基于改进遗传算法的区域交通信号优化控制[J].西华大学学报(自然科学版),2014,33(6):48-52.
[3] 王维松,章伟,王金生.基于FPGA的一种智能交通红绿灯设计[J].计算机应用与软件,2013,30(1):200-204.
[4] 赵庶旭,懂亮.城市交通GPS数据可视化分析[J]. 计算机应用与软件,2016,33(10):279-283.
[5] 钱伟,孙玉娟.城市干线交通信号的模糊协调控制研究[J].河南理工大学学报(自然科学版),2014,33(5):621-624.
[6] 卫星,张利,魏振春,等.交通信号自适应遗传控制算法及仿真研究[J].系统仿真学报,2012,24(11):2255-2258.
[7] Zhang G,Wang Y.Optimizing Minimum and Maximum Green Time Settings for Traffic Actuated Control at Isolated Intersections[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(1):164-173.
[8] Dai Y, Zhao D, Yi J. A comparative study of urban traffic signal control with reinforcement learning and Adaptive Dynamic Programming[C]// International Joint Conference on Neural Networks. IEEE, 2010:1-7.
[9] 张国刚.城市双交叉口信号协调模糊控制与优化算法的研究[D].西南交通大学,2010.
[10] 李欣,李海华.基于模糊控制理论的交通信号控制算法研究[J].电子设计工程,2012,20(2):75-77.
[11] 陈小锋,史忠科.城市交通干线信号动态优化控制方法[J].西北工业大学学报: 自然科学版,2010,28(4):579-584.
[12] 王秋平,舒勤,黄宏观.关于交通流量数据预测建模研究[J].计算机仿真, 2016,33(2):194-197.
[13] 何忠贺,陈阳舟,石建军.切换服务系统的稳定性及交叉口信号配时[J].控制理论与应用,2013,30(2):194-200.
[14] 赖裕平.多级门限服务轮询系统性能分析[D].云南大学,2015.
[15] 郭超勇,刘建强,郑琼林.350km/h动车组TCN网络周期轮询优化算法研究[J].铁道学报,2011,33(12):46-50.
[16] 王润芳,时庆涛.车辆拥堵状态下的最优路径规划建模研究[J]. 计算机仿真, 2016,33(2):204-206.

