基于量化限制容差关系的数据填充算法研究

王旭仁 苏红莉,2 孟 飞 许祎娜

1(首都师范大学信息工程学院 北京 100048) 2(北京国网信通埃森哲信息技术有限公司 北京 100031)

0 引 言

粗糙集理论[1]目前不仅在数据挖掘、数据分析领域取得了巨大成功，还涉及到故障分析、知识获取等领域[2]。这是一种描述不完整数据问题非常有用的数学方法，尤其是为数据挖掘和知识发现领域提供了不同于常规数据库方法一种有效而新颖的理论[3]。如何有效、准确地将粗糙集理论应用于不完备信息系统是粗糙集领域的一个研究热点[4]。

目前常用的ROUSTIDA算法基本思想就是使填充缺失数据后产生的分类规则的支持度应该尽可能的高[5]。研究人员基于ROUSTIDA算法又提出了一些改进算法[6-7]。ROUSTIDA算法和改进的算法都是在基于容差关系模型的基础上[8]，但在相似对象有属性值冲突时，这些数据填充方法填充效果不理想。因此有学者提出基于量化容差关系模型的数据填充算法[9-11]。但当两个对象没有明显相似的属性值时可能会被错误地判定为同一个容差类。

为了解决以上问题，本文结合了限制容差关系和量化容差关系的特点，提出了一种综合量化容差关系和限制容差关系的数据填充方法VLTA。

1 ROUSTID容差关系算法

1.1 容差关系和ROUSTIDA算法描述

定义1令不完备信息系统I=(U,C∪D,V,f)，U={x1,x2,…,xn}是论域，C={ai|i=1,2,…,m}是条件属性集，ai(xj)是样本xj在属性ai上的取值，D是决策属性集。对任何缺少属性值的子集B⊆A，容差关系T可以定义为如公式所示：

∀x,y∈U(TB(x,y)⟺∀Cj∈B(Cj(x)=Cj(y)=*∨Cj(y)=*))

(1)

M(i,j)表示经过扩充的分辨矩阵中第i行第j列的元素，则经过扩充的分辨矩阵M定义为：

(2)

式中：i=1,2,…,m；j=1,2,…,n；“*”表示缺失值[12]。

定义2令不完备信息系统I=(U,C∪D,V,f)，C={ai|i=1,2,…,m}是条件属性集，设xi∈U，则对象xi的缺失属性集MASi，对象xi的无差别对象集NSi和信息系统S的缺失对象集MOS可分别定义为[11]：

MASi={ak|ak(xi)=*,k=1,2,…,m}

(3)

NSi={j|TB(xi,xj),i≠j,j=1,2,…,n}

(4)

MOS={i|MASi≠∅,i=1,2,…,n}

(5)

ROUSTIDA算法步骤如下：

输入：不完备信息系统I0=〈U0,C∪D,V,f0〉。

输出：完备信息系统Ir=〈Ur,C∪D,V,fr〉。

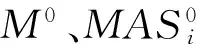
步骤2

2) 产生Ir+1：

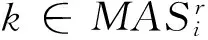
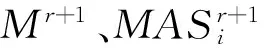
步骤3若信息系统中的数据仍然存在缺失，可以选取平均填充法或组合填充法进行填充。

步骤4计算结束。

1.2 ROUSTIDA算法不足

用一个实例说明ROUSTIDA算法的实施过程，不完备信息表如表1所示。x1、x2、x3是对象，a1、a2、a3、a4是四个取值范围在0到3的属性，“*”代表缺失的属性值。

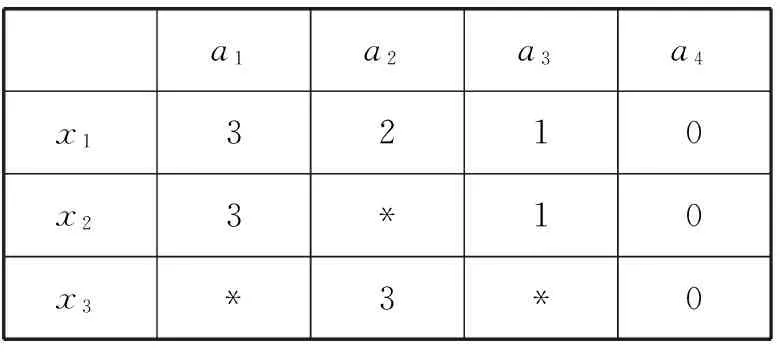
表1 不完备信息表

对象x2的属性a2需要填充。根据定义2，x1、x3都是x2的无差别对象，但两个对象中的a2属性值不同，存在决策冲突，因此x2的a2属性值不能通过ROUSTIDA算法填充。x3的缺失属性不能通过ROUSTIDA算法填充，因为x3的无差别对象集NSi为空。因此从上面实例可以看出，ROUSTIDA算法存在以下不足：

1) 由于ROUSTIDA算法的模型原理简单，在无差别对象中属性值存在填充冲突时，此方法填充效果不理想，就必须通过其他方法填充。

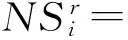
解决的办法之一是使用量化容差关系和相应的算法进行处理。

2 量化容差关系和VTRIDA算法

2.1 量化容差关系和VTRIDA算法描述

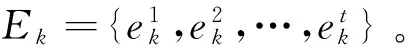
当xi=xj时，Pk(i,j)=1；

否则：

(6)

这样对容差关系T(i,j)进行了量化，两个对象xi、xj的容差关系可以用在所有条件属性上相似的联合概率来度量：

T(i,j)=∏ak∈CPk(i,j)

(7)

量化容差关系矩阵M定义为：

(8)

该算法的计算步骤如下所示：

输入：不完备信息系统I0=〈U0,AT〉。

输出：完备信息系统Ir=〈Ur,AT〉。

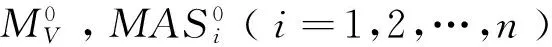
步骤2

1) 生成Ir+1。

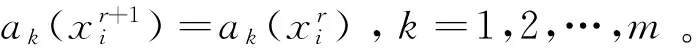
(2) 当i∈MOSr且∃j′,s.t.T(i,j′)=maxT(i,j)则：

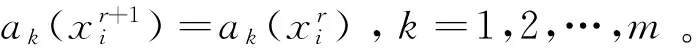
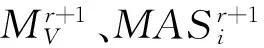
步骤3如果信息系统中的缺失值仍然存在，则需要使用其他算法填充数据，如平均值填充算法和组合填充算法。

步骤4计算结束。

2.2 VTRIDA算法讨论

针对表1可得到量化容差关系矩阵，如表2所示。

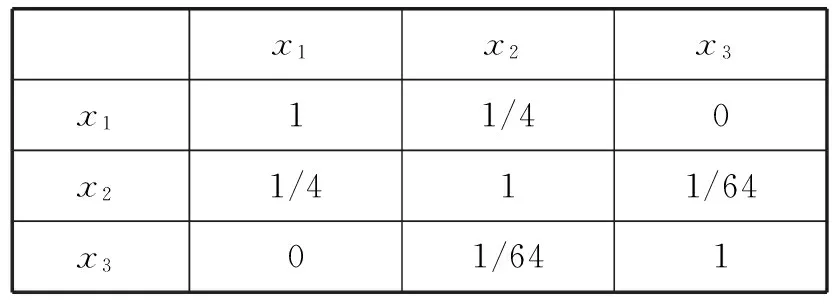
表2 量化容差关系矩阵

填充后得到表1的完备信息表，如表3所示。

表3使用VTRIDA算法得到表1的完备信息表

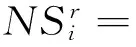
3 基于量化限制容差关系的数据填充算法VLTA

本节在限制容差关系基础上改进了量化容差关系的描述，提出一种新的数据填充算法。

3.1 限制容差关系

定义4给出一个不完备信息系统I=(U,C∪D,V,f)，B⊆(C∪D)且满足PB(x)={b|b∈B∧b(x)≠*}，那么限制容差关系L可以使用公式来表示[13]：

∀x,y∈U×U(LB(x,y)⟺∀b∈B(b(x)=b(y)=*)∨((PB(x)∩PB(y)≠∅)∧∀b∈B((b(x)≠*)∧(b(y)≠*)→(b(x)=b(y)))))

(9)

3.2 改进算法的介绍

一个不完备信息系统I=(U,C∪D,V,f)，B⊆(C∪D)，且PB(x)={b|b∈B∧b(x)≠*}，量化限制容差关系矩阵可以由公式描述：

(10)

式中：Pk(i,j)同式(6)。

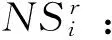
(11)

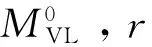
输入：不完备的信息系统I0=〈U0,C∪D〉。

输出：完备的信息系统Ir=〈Ur,C∪D〉。

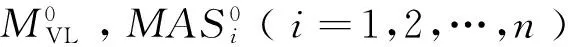
步骤2

2) 生成Ir+1：

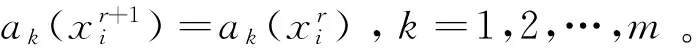
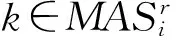
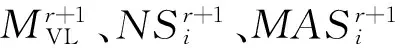
步骤3如果信息系统中仍然存在缺失值，则需要使用其他算法填充数据，例如平均值填充算法和组合填充算法。

步骤4计算结束。

4 结论分析

4.1 理论分析

VLTA与ROUSTIDA、VTRIDA算法填充结果对比

一个不完备信息表如表4所示x1、x2、…、x6是6个对象，a1、a2、a3、a4是四个取值范围在0到3之间的离散属性，“*”代表缺失的属性值。通过ROUSTIDA算法填充后的效果如表5所示，通过VTRIDA算法、VLTA算法填充后的效果分别如表6、表7所示。

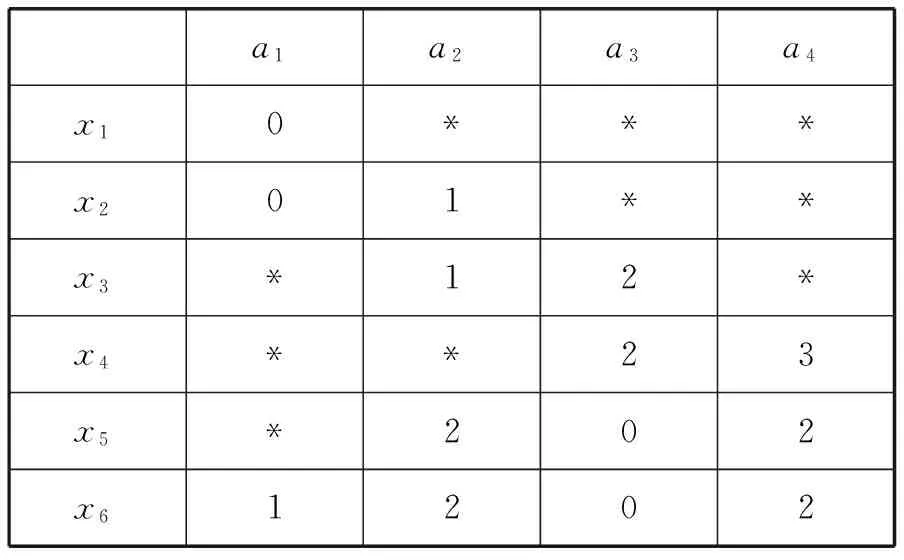
表4 不完备信息表

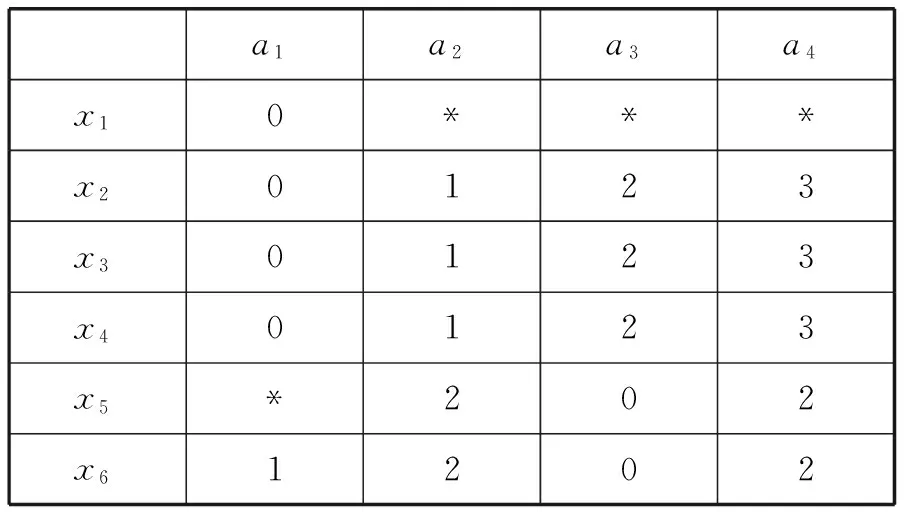
表5 ROUSTIDA填充结果

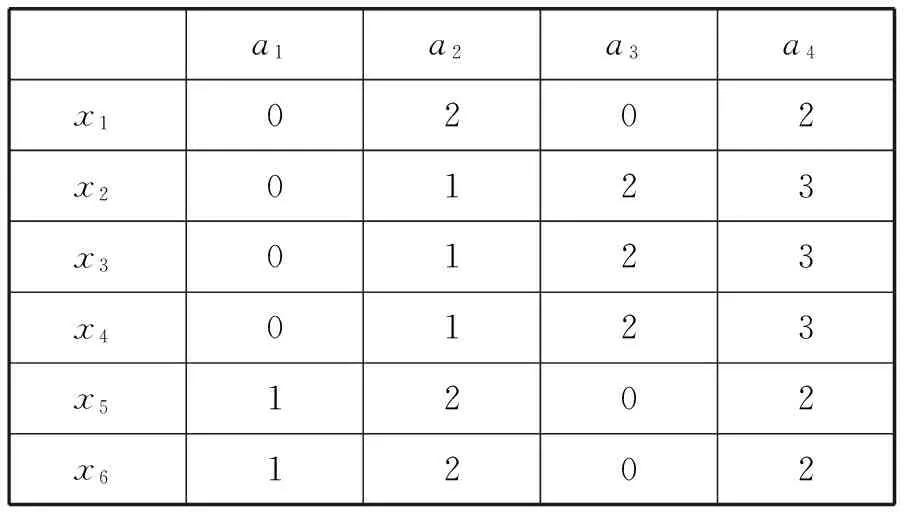
表6 VTRIDA的填充结果

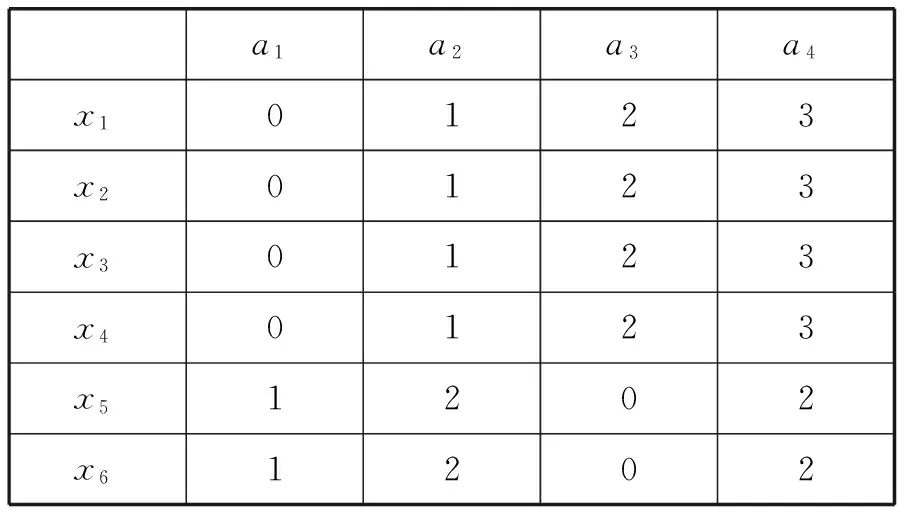
表7 VLTA的填充结果

通过表5可以发现x1和x5的一些属性值不能通过使用ROUSTIDA填充，在此条件下，丢失的数据必须使用其他方法处理。

所有丢失的数据都可以通过使用VTRIDA、VLTA填充完整，填充结果如表6、表7所示。两种算法对表4中的对象x2、…、x6的填充结果一致。而对象x1(0,*,*,*)，算法VTRIDA使用对象x5(*,2,0,2)进行填充，因为在算法VTRIDA下，根据式(6)和式(7)的定义，x1和x5的相似概率最大：

这说明VTRIDA算法中，对容差关系的量化T(i,j)定义不合理，使得属性值完全不同的两个对象(例如表4中的x1和x5)具有最高相似度而进行填充，填充的准确性令人质疑。

4.2 实验分析

将本文提出的VLTA算法部署到基于Spark大数据处理平台，通过算法调用实现对数据的补齐工作。

补齐的数据来自公交车和出租车上安装的采集器，在数据采集过程中采集频率为15秒/次，数据量有500 GB。对从公交车和出租车采集的交通数据22个属性里，选取7个相关性比较强的属性进行数据补齐工作，分别为收集时间、GPS经度、GPS纬度、转速、仪表盘速度和瞬时耗油量。其中仪表盘速度和瞬时耗油缺失情况最严重。

为了VLTA与ROUSTIDA、VTRIDA填充结果对比检验准确性，在原始数据中选取没有丢失的数据集，首先通过随机数据生成器生成一组随机数，在随机数对应的位置挖去属性值造成数据缺失的现象，生成不完备信息系统。

在实验中，处理数据缺失率分别为5%和10%。把数据填充算法：ROUSTIDA、VTRIDA和VLTA分别应用于填充相同的不完备信息系统，平均值填充算法用于填充算法填充后剩余的缺失值。填补正确率使用正确填充的数据量和总缺失的数据量的比值来确定。填充正确率的实验结果如表8和表9所示。

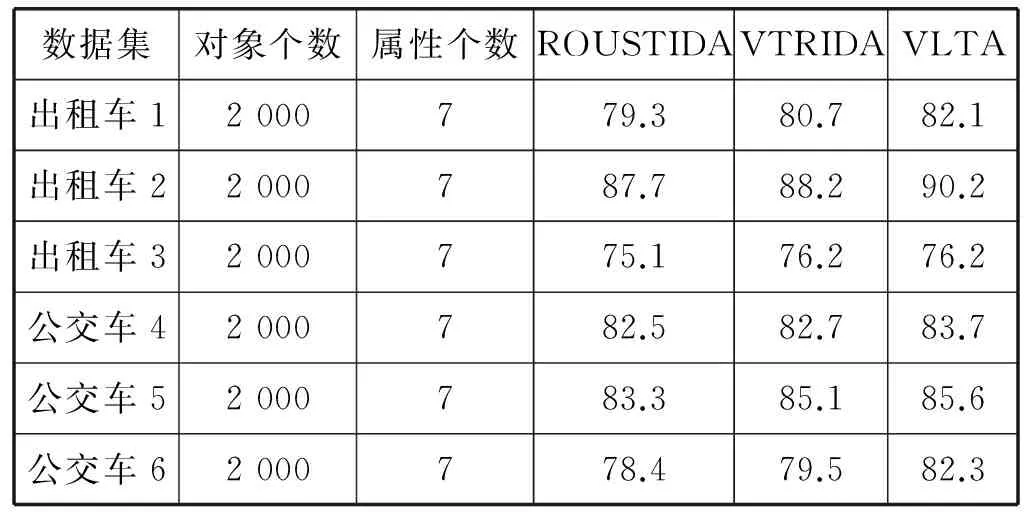
表8 交通数据缺失率为5%实验填充结果对比

表9 交通数据缺失率为10%实验填充结果对比

在不同数据集中，分别用三种算法进行填充，数据填充准确率如图1、图2所示。

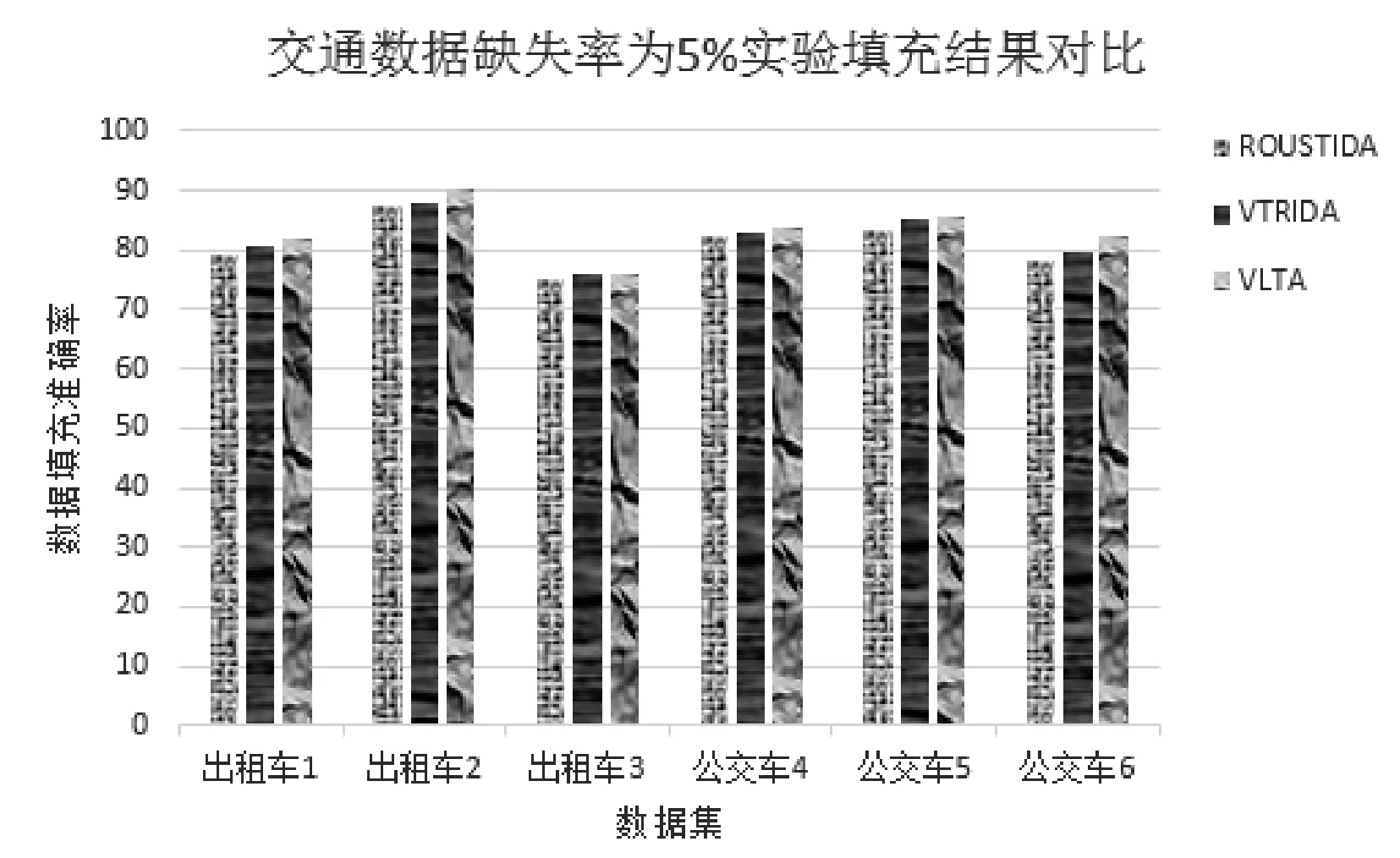
图1 数据缺失率为5%时三种算法的填充准确率对比

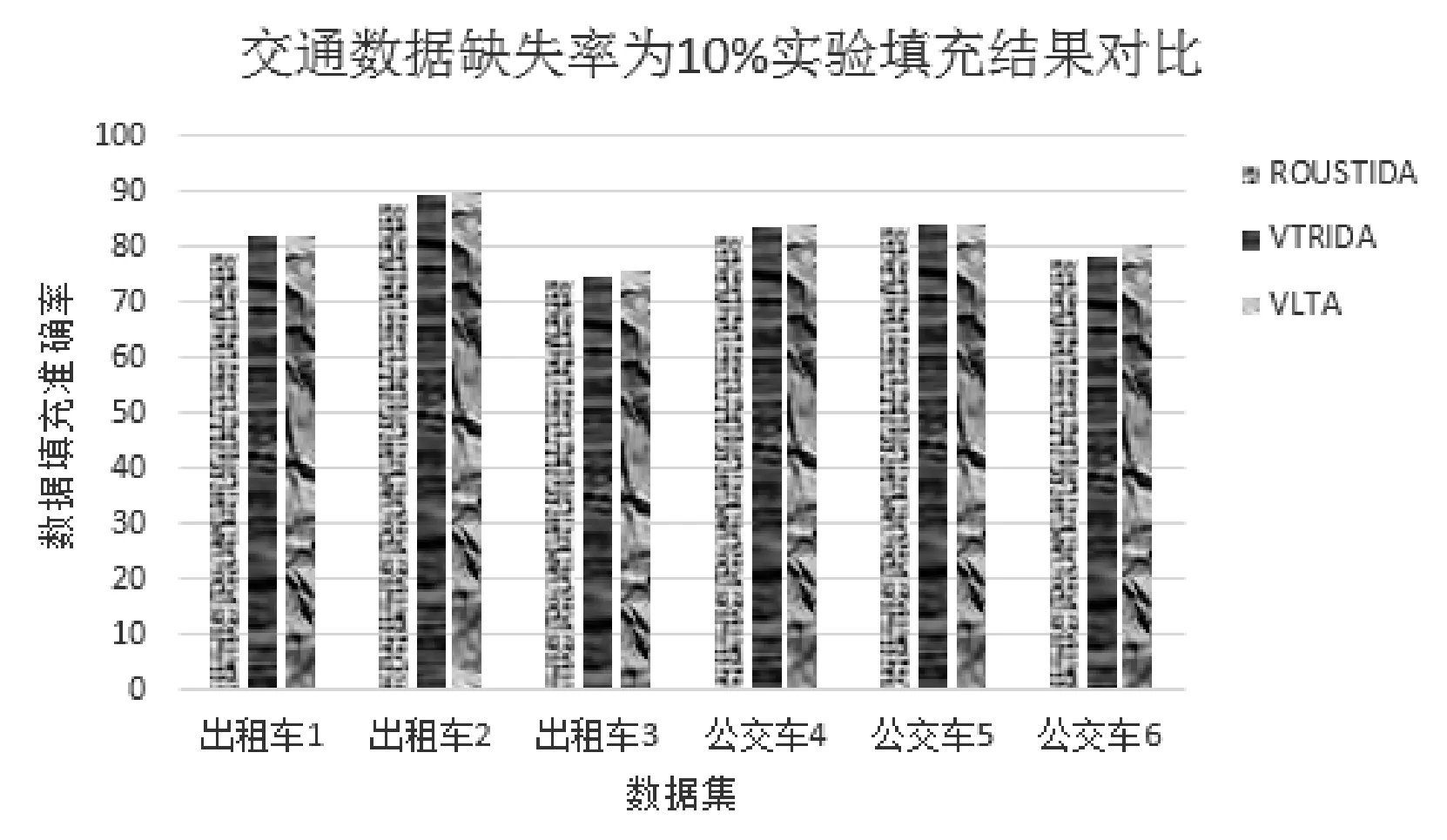
图2 数据缺失率为10%时三种算法的填充准确率对比

观察表8发现，在交通数据缺失率为5%时，出租车缺失数据填充的正确率最高为90.2%，此时对于同一数据集，数据填充正确率相比于ROUSTIDA算法提高2.5%，相比于VTRIDA算法提高2%。公交车缺失数据填充的正确率最高为85.6%，在同一数据集中，数据填充正确率相比于ROUSTIDA算法提高2.3%，相比于VTRIDA算法提高0.5%。

通过表9发现，在交通数据缺失率为10%时，出租车缺失数据填充的正确率最高为90.1%，此时对于同一数据集，数据填充正确率相比于ROUSTIDA算法提高2%，相比于VTRIDA算法提高0.9%。公交车缺失数据填充的正确率最高为84.3%，在同一数据集中，数据填充正确率相比于ROUSTIDA算法提高2.1%，相比于VTRIDA算法提高0.6%。

通过图1和图2可发现，在数据缺失率为5%和10%的不完备信息系统中，在不同数据集下VTLA算法填充结果的准确率高于ROUSTIDA算法和VTRIDA算法。

由此可发现，VTLA算法可以作为数据填充的一种工具，并为数据挖掘工作之前的数据预处理提供支撑工作。

5 结 语

本文分析了ROUSTIDA算法和VTRIDA算法的特点，提出了基于量化限制容差关系的数据填充算法VLTA，优势在于解决以下问题：

(1) ROUSTIDA算法在对数据补齐时，如果容差对象相同的属性值存在冲突，则算法无法对当前对象的缺失值进行补齐，当填充对象无差别对象集为空时，无法对缺失值进行补齐。

(2) VTRIDA算法对容差关系的量化定义过于机械，以至于属性值没有任何相同的两个对象也有可能是容差对象。

实验发现，VLTA算法在数据缺失率不同的不完备信息系统中，数据填充准确度高于ROUSTIDA算法和VTRIDA算法。

本文下一步考虑决策属性值对条件属性值的概率分布的影响，对算法进行改进，使得新的数据填充算法更精确、更科学、填充后的数据更完整。

[1] Pawlak Z. Rough sets[J]. International Journal of Computer & Information Sciences, 1982, 11(5):341-356.

[2] Pawlak Z, Grzymala-Busse J W, Slowinski R, et al. Rough sets[J].Communications of the ACM,1995,38(11):88-95.

[3] 舒文豪. 面向动态不完备数据的特征选择模型与算法研究[D]. 北京交通大学, 2015.

[4] 张亚萍,陈得宝,侯俊钦,等. 朴素贝叶斯分类算法的改进及应用[J].计算机工程与应用,2011,47(15):134-137.

[5] 陈家俊, 苏守宝, 金萍. 一种对象完备度优先填补的决策树规则提取算法[J]. 计算机应用与软件, 2014,31(5):264-267,294.

[6] 丁春荣, 李龙澍. 基于相似关系向量的改进ROUSTIDA算法[J]. 计算机工程与应用, 2014, 50(13):133-136.

[7] 田树新.一种基于改进的ROUSTIDA算法的数据补齐方法[J].海军工程大学学报,2011,23(5):11-15.

[8] 曹佳韵. 基于ROUSTIDA算法的不完整数据处理分析与实现[D]. 东华大学, 2013.

[9] Ding Chun-rong, Li Long-shu. Completing data algorithm based on similarity relation vector[J]. Application Research of Computers, 2013,30(2):383-385.

[10] 王金山, 王磊.基于一种新的量化容差关系的变精度粗糙集模型[J]. 东华理工大学学报(自然科学版), 2013, 36(1):96-100.

[11] 刘城霞, 何华灿. 广义相关性基础上的量化容差关系的改进[J]. 北京邮电大学学报, 2015, 38(5):28-32.

[12] 武森, 冯小东, 单志广. 基于不完备数据聚类的缺失数据填补方法[J]. 计算机学报, 2012, 35(8):1726-1738.

[13] 郭嗣琮, 徐丽, 郑爱红. 限制容差关系的不完备可变粗糙集[J]. 辽宁工程技术大学学报, 2014(7):988-991.