基于功率流理论的星上飞轮隔振效能研究
宋 港,张 利,马 蕾,洪 岩,王继虎,白 杨,齐晓军
(上海卫星装备研究所,上海 200240)
0 引言
航天器在轨运行过程中存在众多扰动源,其中由飞轮转子转动引起的动不平衡造成的宽带谐波扰动是影响有效载荷成像质量的主要扰动源之一[1]。为减小飞轮振动的传递,需进行隔振。隔振设计中,隔振效能是系统结构参数优化设计的重要参考指标。传统的隔振效能评价采用隔振器顶部到底部的振动传递率作为评价指标,当传递率<1时,认为隔振有效。这种评价方法基于如下假设:被隔振体是具有无限质量的绝对刚体;不计隔振器的弹簧和阻尼的质量。而在卫星结构中,飞轮通过隔振支架安装在蜂窝板上,飞轮工作时产生的高频振动使得蜂窝板的弹性模态很容易被激发,此时飞轮与蜂窝板基础间构成了复杂弹性耦合系统,用振动传递率来评价隔振效能就会出现不准确的结果。
隔振系统的功率流理论于 20世纪 80年代由Goyder和White[2]首次提出。振动功率流方法克服了以单一传递率作为评价隔振效能指标的局限,从能量传递的角度来阐释振动传输问题,分析系统的能量传递和分布,为研究复杂弹性耦合系统动力学问题提供了有效途径。振动功率流是一个综合性能指标,兼顾了力和速度以及它们的相位关系,包含信息丰富,可替代传统隔振指标用于结构振动控制性能的评价。因此,近年来振动功率流理论已被广泛应用于柔性结构的隔振设计中[3-7]。
本文将振动功率流理论应用于星上飞轮隔振支架的隔振效能研究,考虑隔振器的驻波效应以及基础的非刚性因素对功率流传递特性的影响,运用子系统导纳矩阵法建立柔性基础上飞轮隔振系统动力学模型,推导出系统的功率流传递函数表达式。以功率流传递率作为评价隔振效能的指标,通过数值仿真计算分析结构参数对隔振效能的影响,为系统结构参数的优化设计提供参考依据。
1 飞轮隔振系统动力学建模
飞轮隔振系统一般由飞轮、隔振支架和飞轮安装板(蜂窝板)组成。为便于理论建模,将飞轮和隔振支架组合体看成具有规则几何形状的刚体,其所有内部激励力的作用点都在组合体质心上;将隔振器简化为具有连续分布质量的圆筒形弹性杆;飞轮安装板用四边简支矩形薄板模拟。飞轮隔振系统简化模型如图1所示。
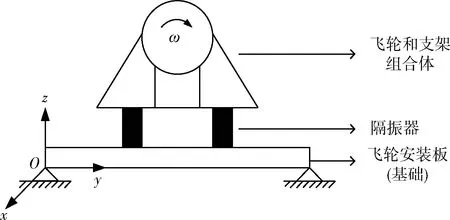
图1 飞轮隔振系统简化模型 Fig.1 The simplified model of the flywheel vibration isolation system
飞轮隔振系统可分为3个子系统:飞轮与支架组合体子系统A;隔振器子系统B;基础子系统C。整个系统关于平面yOz对称,因此可以将系统的三维复杂空间模型简化为平面问题处理。为便于分析,假设有3个同频率的简谐激励力(力矩)作用于飞轮与支架组合体的质心:y向的横向简谐激励力,z向的纵向简谐激励力和绕x轴的倾倒力矩。用FAt、FAb分别表示子系统A的输入端力与输出端力,FBt、FBb分别表示子系统B的输入端力与输出端力,与其相应的输入与输出端响应速度分别用VAt、VAb、VBt、VBb表示。子系统C受到的力记为FC,相应的响应速度记为VC。
1.1 飞轮与支架组合体子系统动力学建模
飞轮与支架组合体子系统受力分析如图2所示。
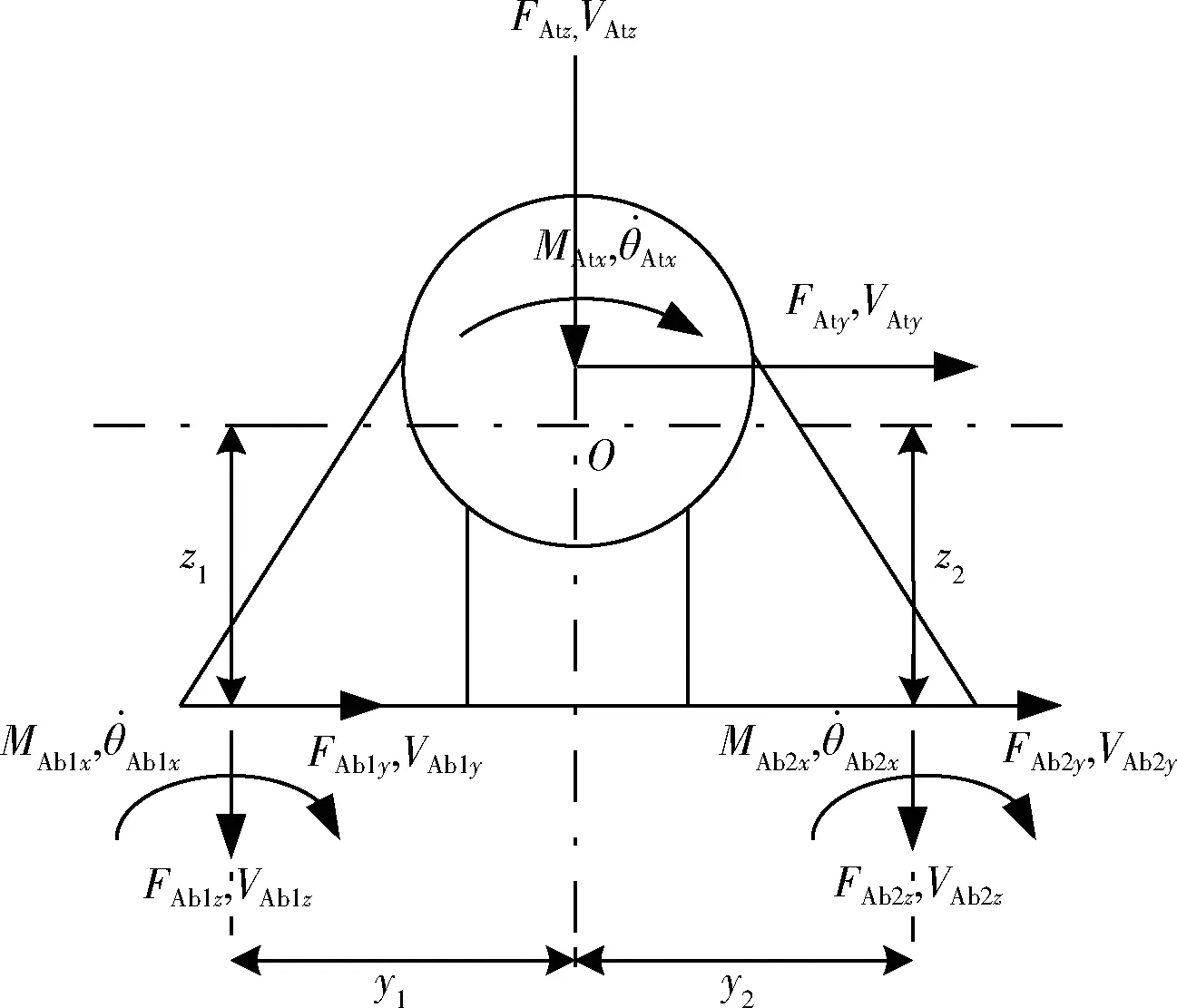
图2 飞轮与支架组合体受力分析 Fig.2 Force analysis of the flywheel and bracket assembly
根据刚体动力学相关理论,可建立方程:

式中:mA为飞轮与支架组合体质量;JA为组合体绕x轴的转动惯量;ω为简谐激振力频率;y1、y2分别为子系统底部受力点到质心的横向距离;z1、z2分别为子系统底部受力点到质心的垂向距离;其他各参数参见图2标注。将式(1)写成矩阵形式:
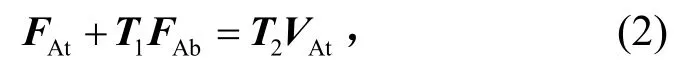
式中T1、T2为转换矩阵。
同样,根据刚体运动学理论建立运动学方程为
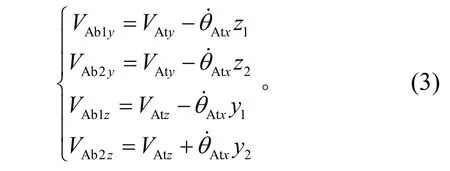
将式(3)写成矩阵形式:

综合式(2)、式(4)可得子系统A的动力学方程
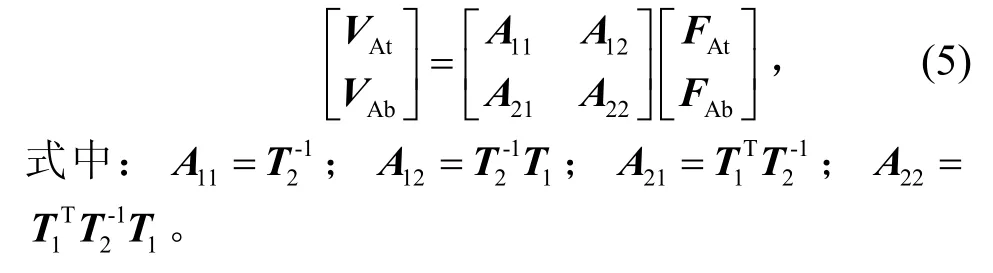
1.2 隔振器子系统动力学建模
实际工程中用到的隔振器为具有质量的连续分布体,当激励频率接近隔振器固有频率时,就会发生共振。此时高频声将以弹性波的形式在隔振器中传播进而产生驻波效应,使得隔振器的隔振性能降低20 dB之多[8]。基于上述考虑,为真实反映隔振器特性,将航天领域常用的横槽型弹簧隔振器简化为圆筒形弹性杆模型,对其进行动力学分析与建模,如图3所示。
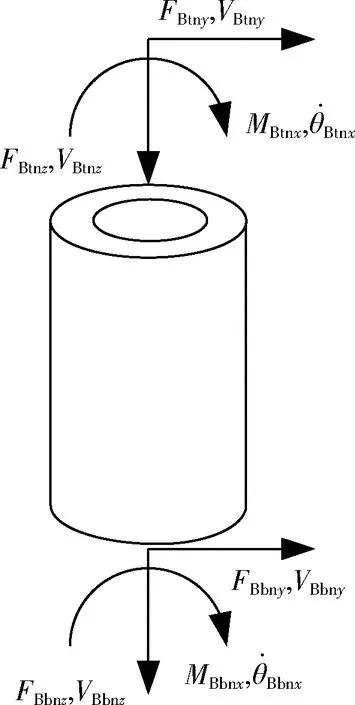
图3 隔振器受力分析 Fig.3 Force analysis of the vibration isolator
记第n个隔振器上、下端受到的力和速度分别为:
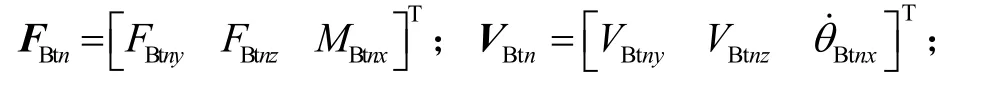

运用模态分析法,可以得到第n个隔振器的速度导纳矩阵为

假设子系统 B由两组隔振器构成,则隔振器子系统B的动力学方程为

1.3 基础子系统动力学建模
将飞轮安装板用四边简支矩形薄板来模拟,其受力分析如图4所示。

图4 飞轮安装板受力分析图Fig.4 Force analysis of the flywheel mounting plate
由薄板弯曲振动理论,列出板的振动微分方程
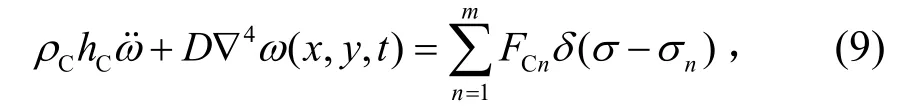
由模态理论可推得四边简支板在稳态强迫振动下的动力学方程为

式中Cij(i,j=1,2)的具体表达式参见文献[10]。
2 系统功率流传递谱推导
各子系统间的传递力和相应的速度关系为:

由式(11)结合式(5)、(7)和(10),可以得到各子系统交界处的速度和力:。其中:。
由振动功率流理论,可得输入各子系统的功率流PA、PB、PC分别为:。其中上标H表示矢量或矩阵的共轭转置。
3 数值仿真与计算
飞轮与支架组合体质量mA=12.7 kg,组合体绕x轴的转动惯量JA=0.508 kg·m2;隔振器外径D=0.066 m,内径d=0.046 m,高h=0.08 m,弹性模量EB=6.5 MPa,惯性矩IB=7.12×10-7m4,损耗因子ηB=0.1;飞轮安装板密度为ρC=2700 kg/m3,杨氏弹性模量EC=71 GPa,剪切弹性模量GC=24 GPa,阻尼损耗因子δC=0.01,安装板尺寸2 m×1.5 m×0.015 m。计算实例中,弹性基础板截取前32阶模态,所截取的模态数目覆盖了需要考察的频率范围,可以获得足够的精度。假设飞轮工作时由转子动不平衡带来的扰动力为y向的横向力、z向的纵向力和绕x轴方向的倾倒力矩作用,且y、z方向的力均为幅值为1的简谐激励力。输入各子系统的时间平均功率流单位均为dB,基准功率流取为Pref=10-12W。
3.1 输入各子系统的功率流特性
飞轮隔振系统输入各子系统功率流传递谱如图5所示。从图中可以看出,输入子系统A的功率流曲线PinA与输入子系统B的功率流曲线PinB相重合,这是因为子系统 A为刚体,能量经过刚体传递后没有损失。PinA在15.2、23.6、24.9 Hz处出现3个峰值,分别对应子系统A的横向、纵向和旋转运动刚体模态。PinA在507.1 Hz处也出现了峰值,这是因为外激励频率达到了隔振器的纵波共振频率使得隔振器产生驻波效应所致。
系统在低频域的隔振效果不明显,PinA和输入到基础子系统 C的功率流曲线基本重合在一起。随着激励频率的增加,PinC的下降趋势逐渐加快,但高频段激起基础的弹性模态使得PinC出现了多个峰值,这些因素都影响了整个飞轮隔振系统的高频隔振能力,而采用传统的振动传递率来评价隔振效果时会忽略这些因素的影响,使得评价结果不准确。

图5 各子系统功率流传递谱曲线Fig.5 The power flow transmitted to each subsystem
单向激励下传递到基础的功率流情况如图6所示。从图中可以看出,在30 Hz之前的低频段,纵向力和倾倒力矩都对传递到基础的功率流起主导作用,两者作用相当,横向力传递到基础的功率流略小于前两者。在中高频域,倾倒力矩激励对传递到基础的功率流影响大于纵向力激励和横向力激励的影响。因此在隔振设计中不能忽略倾倒力矩激励的作用。
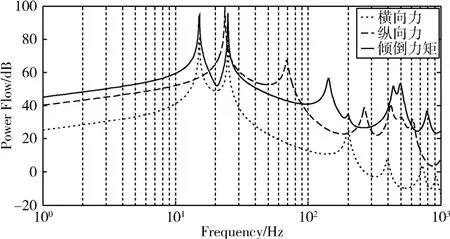
图6 单向激励下传递至基础的功率流Fig.6 The power flow transmitted into the foundation with single excitation
混合激励下传递到基础的各功率流分量如图7所示。从图中可以看出:由传递到基础的纵向力和相应的纵向速度响应引起的纵向功率流所占比例最大;其次为由传递到基础的力矩和相应的角速度响应引起的旋转功率流;由传递到基础的横向力和相应的横向速度响应引起的横向功率流所占比例最小。由于传递到基础的纵向力直接引起基础的横向振动,此时基础的振动以弯曲波形式传播,这也说明了弯曲波在弹性基础的能量传播中占主导地位。

图7 混合激励下传递至基础的功率流分量Fig.7 The power flow component transmitted into the foundation with combined excitation
3.2 系统结构参数对隔振性能的影响
为了更加直观地衡量飞轮隔振系统的隔振效果,采用功率流传递率γ作为定量评价标准。该评价指标定义为输入子系统A(飞轮与支架组合体)和输入子系统C(基础)的功率流对数之比,其形式为
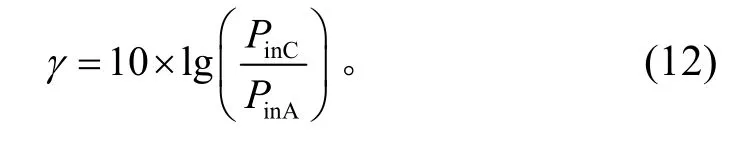
当γ<0时,表明系统隔振作用有效。
图8为飞轮与支架组合体质量改变时,系统功率流传递率的变化情况。从图中可以看出,增大组合体质量使得系统的刚体运动模态向低频域偏移,功率流传递率曲线在中、高频域无明显变化。
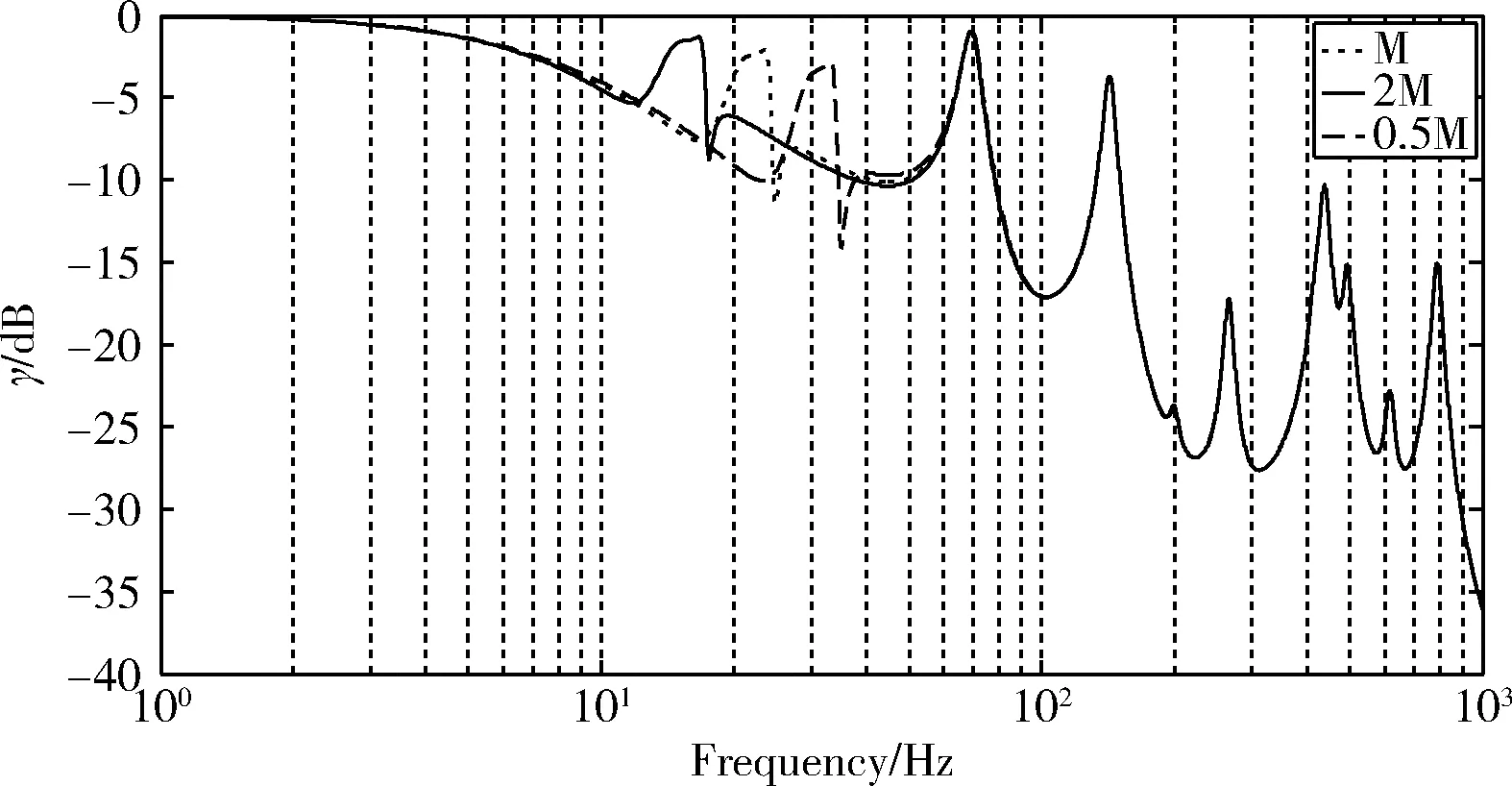
图8 飞轮与支架组合体的质量对隔振性能影响Fig.8 The effect of the mass of flywheel and bracket assembly on vibration isolation performance
隔振器弹性模量、阻尼系数对功率流传递率的影响分别如图 9、图 10所示。减小隔振器弹性模量(相当于减小隔振器刚度),系统功率流传递率相应降低,随之系统的刚体模态频率向前偏移,对系统隔振有利,但同时也要考虑隔振器刚度对系统侧向稳定性的影响。隔振器阻尼系数的增大会使功率流传递曲线整体降低,但不改变功率流传递曲线的峰值频率。
基础厚度对隔振性能的影响如图11所示。从图中可以看出,增加基础厚度相当于增大基础抗弯强度,使得基础的固有频率也相应增加,基础共振峰值点整体向高频域偏移。总体来说,增加基础厚度可以降低传递到基础的功率流。图12所示为基础阻尼系数对隔振性能的影响,基础阻尼系数越小,功率流传递率相应减小,隔振效果越好,但共振频率处的峰值会变大。为了降低系统通过共振区时的峰值,必须选择适当的阻尼。
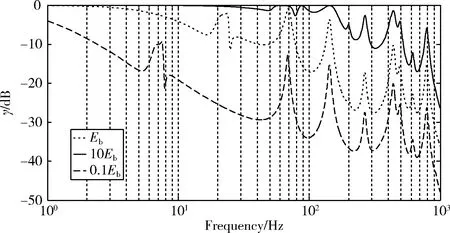
图9 隔振器刚度对隔振性能的影响Fig.9 The effect of isolator stiffness on vibration isolation performance

图10 隔振器阻尼系数对隔振性能的影响Fig.10 The effect of isolator damping coefficient on vibration isolation performance
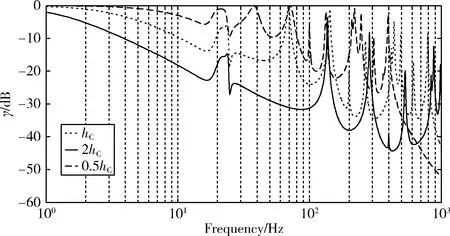
图11 基础厚度对隔振性能的影响Fig.11 The effect of the plate thickness on vibration isolation performance

图12 基础阻尼系数对隔振性能的影响Fig.12 The effect of the plate damping coefficient on vibration isolation performance
4 结论
1)飞轮隔振系统在低频域的隔振效果一般,此时系统主要以飞轮与支架组合体的刚体运动模态为主。在中、高频域,传递到基础的功率流明显降低,但由于受到隔振器驻波效应及基础的弹性模态等因素影响,使得在高频域内输入基础的功率流下降趋势变缓,隔振效果受到一定的影响。
2)在低频域,纵向力激励和倾倒力矩激励都对传递到基础的功率流起主导作用,两者作用相当;在中、高频域,倾倒力矩激励对传递到基础的功率流影响大于纵向力激励和横向力激励的。传递到基础的功率流各分量中,以传递到基础的纵向力和相应的纵向速度响应所引起的纵向功率流最大。
3)减小隔振器刚度或增加隔振器阻尼,均可以减小系统的功率流传递率,对系统隔振有利。增加基础厚度可以使基础的弹性共振模态推迟发生,同时也降低了系统的功率流传递率;增大基础阻尼使得功率流传递率峰值减小,但在峰值以外功率流变大,对系统隔振不利。
(References)
[1]董瑶海.航天器微振动——理论与实践[M].北京:中国宇航出版社,2015: 30-39
[2]GOYDER H G,WHITE R G.Vibration power flow from machines into built-up structures: Part I Introduction and approximate analyses of beam and plate-like foundations[J].Journal of Sound and Vibration,1980,68(1): 59-75
[3]CHOI W J,XIONG Y P,SHENOI RA.Power flow analysis for a floating sandwich raft isolation system using a higher-order theory[J].Journal of Sound and Vibration,2009,319(1): 228-246
[4]承颖瑶,陈龙祥,蔡国平.柔性被动隔振系统的功率流传递特性研究[J].动力学与控制学报,2009,7(4):368-374 CHENG Y Y,CHEN L X,CAI G P.Power transmission characteristics of flexible passive isolating system[J].Journal of Dynamics and Control,2009,7(4): 368-374
[5]牛军川,宋孔杰.多激励多支承全柔性隔振系统的传递特性分析[J].机械工程学报,2011,47(7): 59-64 NIU J C,SONG K J.Transimission characteristics of fully flexible isolation systems subjected to multi-excitations and supported by multi-mounts[J].Journal of Mechanical Engineering,2011,47(7): 59-64
[6]楼京俊,李超博,夏江敏,等.柔性隔振系统功率流传递特性研究[J].船舶工程,2016,38(7): 31-34 LOU J J,LI C B,XIA J M,et al.Research on power flow transmission characteristics of flexible isolation system[J].Ship Engineering,2016,38(7): 31-34
[7]肖和业,盛美萍,任杰安.梁板耦合建模中连接负载对系统功率流特性影响研究[J].工程力学,2012,29(7): 6-11 XIAO H Y,SHENG M P,REN J A.Study of effects of connecting load on character of power flow among coupled system in beam-plate coupled system modeling[J].Engineering Mechanics,2012,29(7): 6-11
[8]熊冶平,宋孔杰.柔性隔振系统中驻波效应的研究[J].山东工业大学学报,1995,25(2): 108-113 XIONG Y P,SONG K J.Research of the wave effects in flexible isolation system[J].Journal of Shandong University of Technology,1995,25(2): 108-113
[9]孙玲玲,宋孔杰.复杂机械系统多维耦合振动传递矩阵分析[J].机械工程学报,2005,41(4): 38-43 SUN L L,SONG K J.Transmission matrix method for multi-dimensional vibration analysis of complex mechanical systems[J]. Journal of Mechanical Engineering,2005,41(4): 38-43
[10]GARDONIO P,ELLIOTT S J, PINNINGTON R J.Active isolation of structural vibration on a multi-degree-of-freedom system: Part I The dynamic of the system[J].Journal of Sound and Vibration,1997,207(1): 61-93

