基于Creo Simulate进行连杆失稳分析

上海交通大学材料科学与工程学院 宓宝江

龙口隆基三泵有限公司 王常勇

本文基于机构动力学模拟获取连杆真实受力，导入到Creo Simulate环境进行静力分析，在此基础上对连杆进行线性失稳和非线性失稳分析计算，探讨非线性失稳的初始缺陷设置方法，对线性和非线性失稳分析结果进行比较，给出在Creo Simulate中进行连杆失稳分析的有效途径。

一、连杆概述

连杆是发动机、压缩机等主要的传动构件之一，它将活塞和曲轴连接起来，把作用于活塞顶部的膨胀气体压力传给曲轴，使活塞的往复直线运动可逆地转化为曲轴的回转运动。连杆由连杆体、连杆盖、连杆螺栓和连杆轴瓦等零件组成，连杆体与连杆盖分为连杆小头、杆身和连杆大头。连杆小头用来安装活塞销，以连接活塞。杆身通常做成“I”或“H”形断面，以求在满足强度和刚度要求的前提下减少质量。连杆大头与曲轴的连杆轴颈相连。一般做成分体式，与杆身切开的一半称为连杆盖，二者靠连杆螺栓连接为一体。连杆轴瓦安装在连杆大头孔座中，与曲轴上的连杆轴颈装配在一起。

根据连杆的工作属性，连杆应该具有足够的强度、刚度和稳定性。就其稳定性而言，由于连杆的形状和载荷复杂，采用传统的欧拉公式或经验公式往往得不到满意的设计结果，尤其是随着用户对产品及质量和安全性能的要求不断提升，汽车制造厂商对连杆制造提出来更高要求，其中一项就是连杆的稳定性验算，保证连杆在正常工作过程中不会因为失稳而导致意外事故。

二、失稳分析

失稳又称屈曲，分为线性和非线性分析计算类型。采用公式校核连杆屈曲时，一般截取杆身中部某一位置截面，取连杆的大小头孔中心距离作为杆长，把连杆近似看作等截面的压杆。连杆在不同方向发生屈曲，其等效长度也不同。连杆并非细长压杆，不能采用大柔度杆欧拉公式校核，一般用经验功能公式计算。当前使用更多的是利用有限元方法对连杆稳定承载能力进行更为精确地稳定性计算。

屈曲分析一般有两步，首先是特征值屈曲分析，此分析为线性屈曲分析，是在小变形的情况进行的，即模态，目的是得出临界荷载。其次，就是后屈曲分析，此步一般定义为非线性，原因在于是在大变形情况进行的，一般采用位移控制加修正的弧长法，可以定义材料非线性，以及几何非线性，加上初始缺陷，所以也称为非线性屈曲分析。此步分析，为了得到极限值，需要得出荷载位移曲线的下降段。缺陷较小的结构初始位移变形较小，在极值点突变，而初始缺陷较大的结构，载荷位移曲线较平滑。

非线性屈曲分析是大变形的静力分析，相对于线性屈曲分析更加精确，其充分考虑了几何、材料、边界等非线性行为，可分析结构的不稳定倒塌（大变形失稳）、弹塑性失稳和后屈曲失稳等。由于引入了非线性行为，相对线性屈曲分析计算时间较长。使用和线性屈曲分析相同的约束，设置大变形非线性选项，勾选“突弹跳变”选项，设置弹塑性材料，运行非线性分析。

设置非线性分析初始缺陷可以通过导入屈曲模态模型信息的方法进行。ANSYS、Abaqus等专业软件都有专门的导入屈曲模态的操作命令，直接输入导入的模态阶数和比例因子即可。在Creo Simulate中没有直接操作命令，可以将线性屈曲一阶模态模型保存备份为wrl文件，再在Creo Parametric环境导入保存为小平面曲面模型，接下来有下列处理方法：（1）根据小平面曲面模型，创建精确的参数化初始缺陷模型，这是最为精确的带初始缺陷模型。（2）测量小平面模型的变形弯曲角度，适用该角度对实际模型执行实体折弯操作，根据形状变化较为准确地构建初始缺陷模型。（3）在弯曲方向上施加强制位移（相当于预加一个载荷，具体分析时再撤去），位移值通过一阶线性屈曲模态形状确定，该方法在参考位置处产生应力集中，仅仅用于粗略估算。

三、连杆的线性屈曲分析

1.连杆受力分析

失稳分析计算必须输入作用在连杆上的实际受力，因此，必须对连杆进行合理的受力分析，曲柄连杆机构受力具体情况如图1所示。

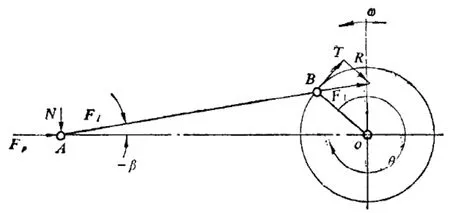
图1

通过曲柄连杆机构动力学模拟获得连杆的压力情况，如图2所示。使用连杆的最大受力值作为基准，和后面的屈曲分析临界载荷进行比较，确认连杆是否满足稳定性要求。

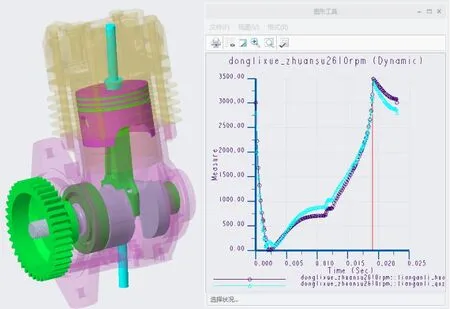
图2

2.连杆线性屈曲分析

（1）定义和运行静态分析。

进行线性屈曲分析需要先运行基础的静态分析。设置材约束条件：对于小头柱面，创建小头中心点和柱面刚性连接；参照中心点，释放柱面轴向旋转自由度，约束其余5个自由度。对于大头柱面，创建大头中心点和柱面刚性连接；参照中心点，释放柱面轴向旋转、连杆拉压方向平移两个自由度，约束其它4个自由度。设置载荷：为了便于查看临界屈曲载荷，设置载荷值1000N，这样临界载荷因子的值就是临界载荷的值（单位kN），如图3所示。

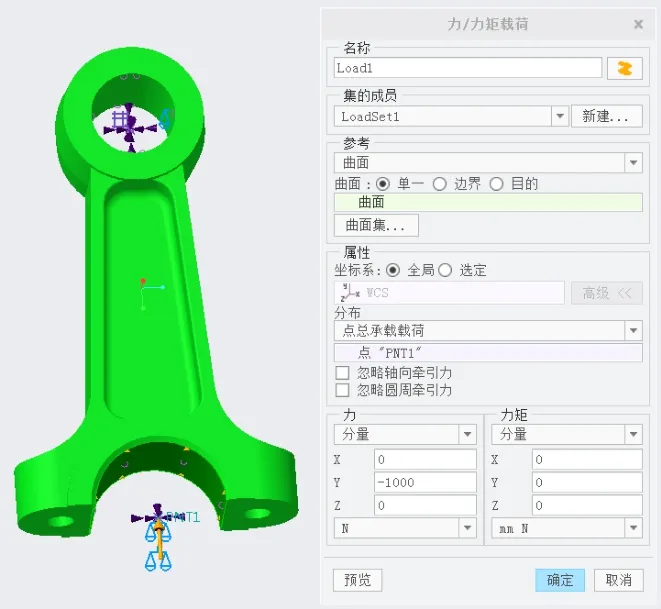
图3

（2）定义和运行线性屈曲分析。

基于该静态分析定义线性屈曲分析。旋转载荷集，设置失稳模态数。查看线性屈曲分析结果。

①查看摘要报告（图4）。线性屈曲分析时设置初始载荷1kN，也就是临界载荷因子。分析计算了4阶模态，第一阶特征值为1041kN，第二、三、四阶特征值分别为1120、1133、1233kN。当屈曲发生时，连杆会首先发生第1阶屈曲模态变形，如果外载在内侧方向由扰动，也有可能发生第2-4阶屈曲变形。

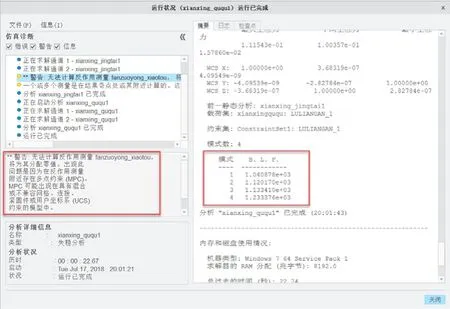
图4

②线性屈曲模态变形图（图5）。第1阶屈曲模态为连杆受挤压后最先出现的屈曲变形，此时连杆为侧向单方向弯曲；第2阶屈曲为杆身腔壁压弯变形（双环），顶面、底面不同形状；第3阶屈曲为杆身腔壁压弯（单环）和顶底面弯曲；第4阶屈曲为杆身腔壁压弯（双环）和顶底面弯曲，两面不同形状。

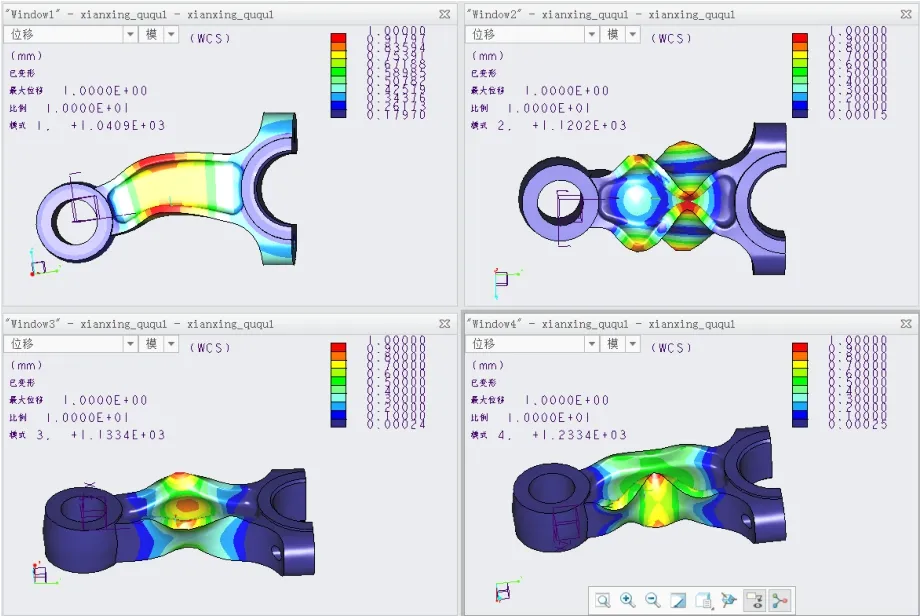
图5

线性屈曲载荷为1041kN，然而在此载荷下，连杆已经因为屈服而发生失效。所以线性特征值屈曲分析得到的屈曲载荷偏高，不能给出准确的屈曲载荷，只能预测零件屈曲的敏感性和变形特征。主要原因是该连杆并不属于经典欧拉公式所要求的长柔度杆或薄壁管件。因此需要进一步对连杆进行非线性屈曲分析。

四、连杆非线性屈曲分析

1.构建用于非线性屈曲分析的初始缺陷模型

（1）构件线性屈曲模型的一阶屈曲模态位移结果，比例是1（图6）。

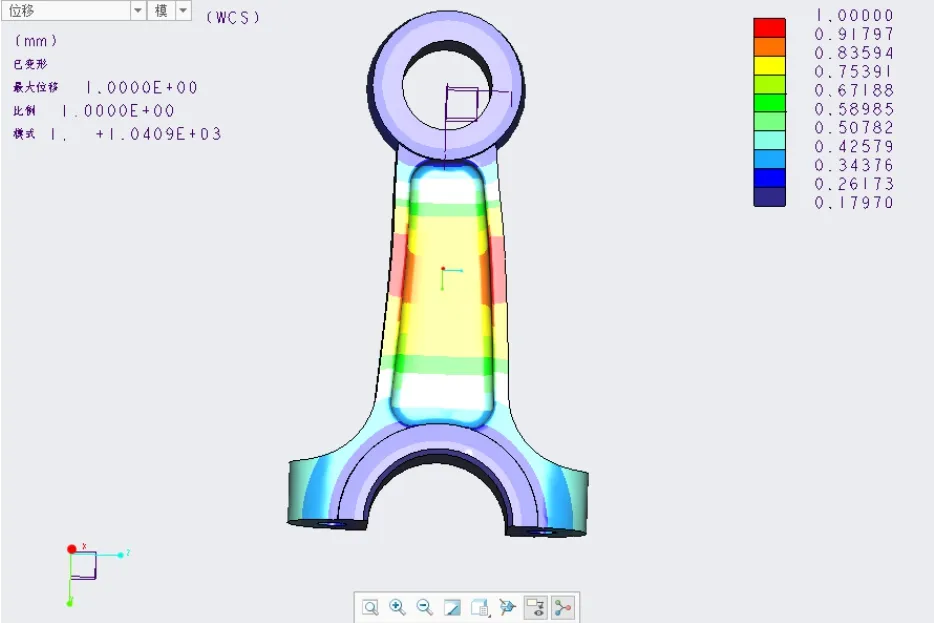
图6

（2）Simulate结果界面，文件＞另存为＞保存备份＞选择文件类型VRML文件类型（*.wrl）＞保存，例如liangan_xianxing_ququ_modal1.wrl。

（3）在CreoParametric环境，打开wrl文件，选择文件，点击“导入”。

（4）选择合适的零件模板，使用缺省的坐标系，生成小平面曲面模型。

（5）保存副本为“收缩包络”模型，多面实体，质量10级。

（6）打开收缩包络模型，可以测量屈曲模态弯曲角度，创建模型弯曲变形状态；也可以测量载荷参考点偏转坐标值，以推算载荷扰动因子。这里采用弯曲角度测量方案。如图7所示偏转三角形，测量小锐角。

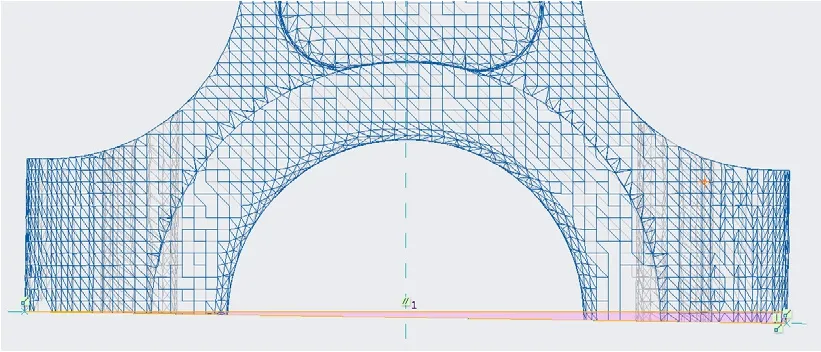
图7

（7）构建实体折弯，补建大小头圆柱孔曲面。

根据现行屈曲模态振型偏角，创建实体折弯草绘曲线，为了便于施加载荷，假定大头不变，旋转小头。执行骨架折弯命令。执行实体折弯后，需要重新构建大头、小头圆柱孔几何。重新编辑约束、载荷的参照（图8）。

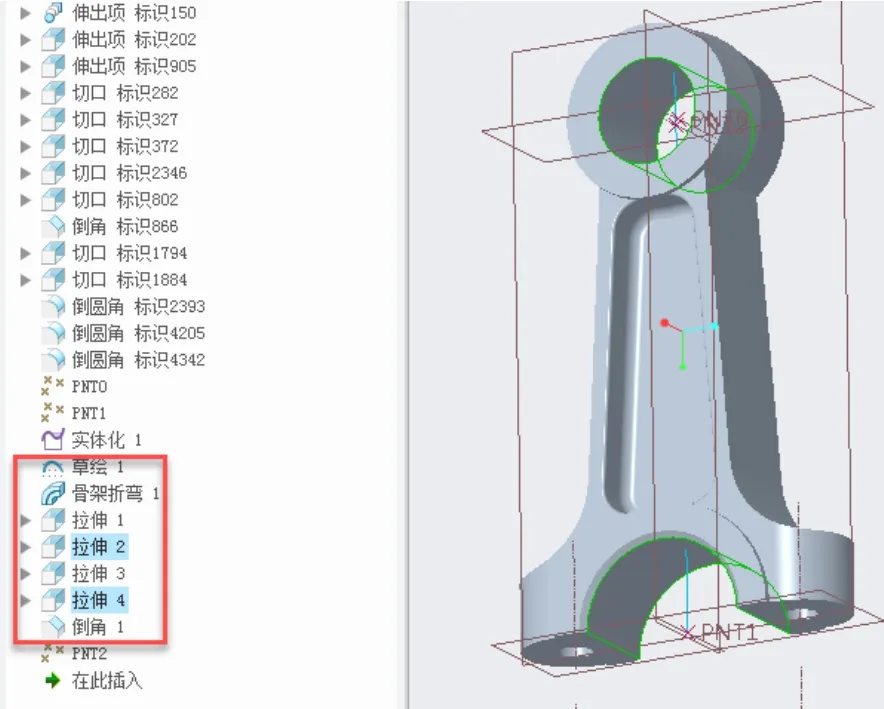
图8

2.定义弹塑性材料

钢之类的金属对小载荷表现出弹性行为。载荷进一步增加时，材料将承受塑性变形。这类材料称为弹塑性材料。Creo Simulate使用各向同性硬化定律定义弹塑性材料。硬化定律是描述材料流动应力和有效应变之间关系的规则。对于硬化材料，屈服曲面在空间上扩展。屈服曲面沿所有方向与应变增量成比例地扩展。使用下列方法之一可以定义弹塑性材料：使用测试数据；使用材料常数。

显示的材料常数根据做出的选择而变化：理想塑性、线性硬化、幂次定律、指数定律。还必须为弹塑性材料指定“热软化系数”和“拉伸屈服应力”（图9）。

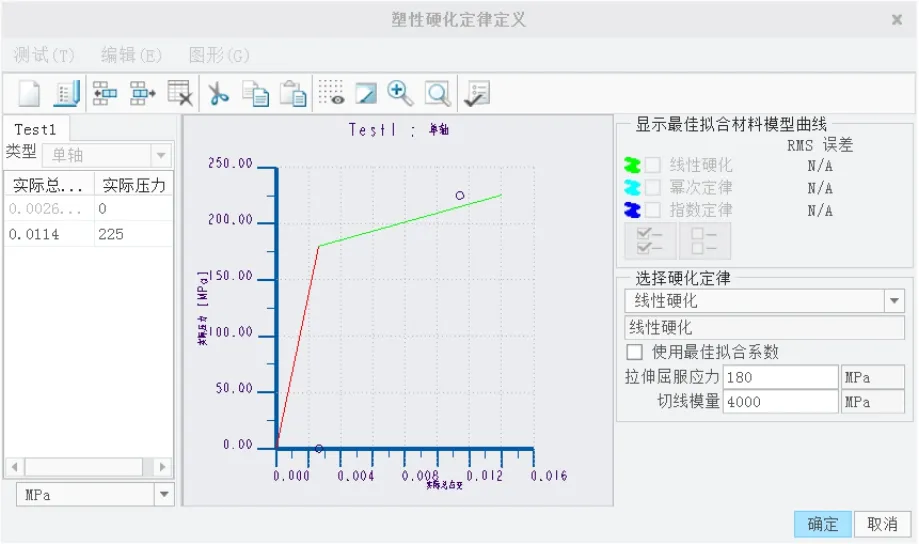
图9

3.定义测量

定义约束反作用测量，约束创建时必须参考世界坐标系。定义载荷作用点位移测量，该点要设置为硬点。

4.设置边界条件

（1）约束条件：同线性静态分析的约束设置。

（2）载荷条件。

在连杆大头处施加线性连续集中载荷，这个值必须要高于塑性屈曲载荷。设置一个预估值，如果未能出线屈服，则加大载荷继续求解；如果载荷过大，分析可能不收敛，则从分析不收敛结果查看更为合适的载荷。进行非线性分析，添加连杆材料的塑性特性参数，而且已经引入线性屈曲第1阶模态作为初始缺陷，表达几何或者载荷的扰动。这里使用100kN、50kN、30kN进行计算，创建三个载荷集，分三个分析定义进行（图10）。

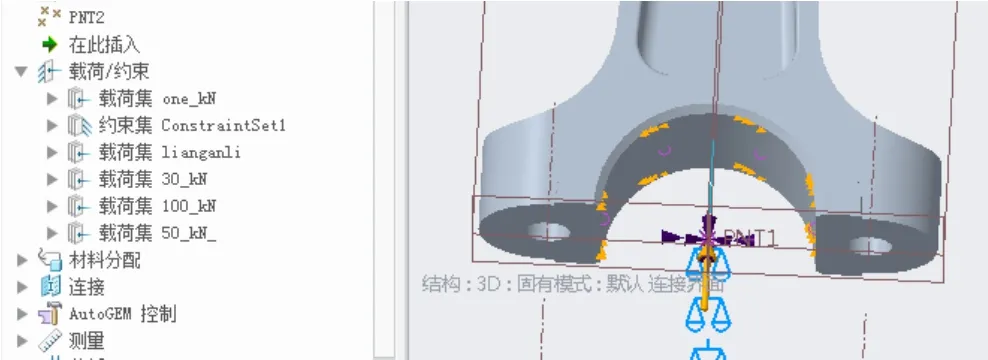
图10

5.定义和运行分析

创建静态分析（图11），设置非线性选项：计算大变形、塑性、包括突弹跳变。输出选项：设置21个主步，总载荷因子为1，等间距。

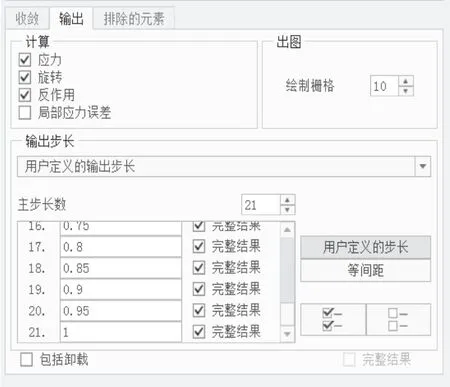
图11

分别运行三种分析，注意载荷集的不同选取。

（1）首先使用第一阶屈曲分析的临界载荷的十分之一，即100kN运行分析，监测到突弹跳变，但是运行分析失败，主要是由于载荷过大，改为成更小的载荷再次计算（图12）。

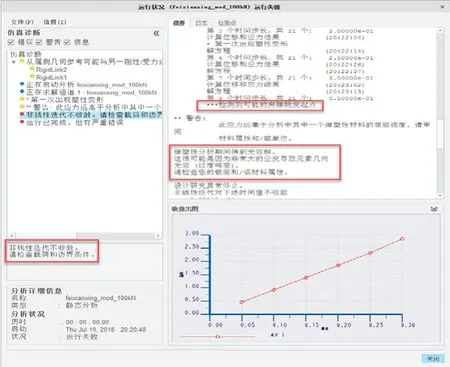
图12

（2）使用35kN载荷计算，分析收敛，但是没有检测到“突弹跳变”（图13）。

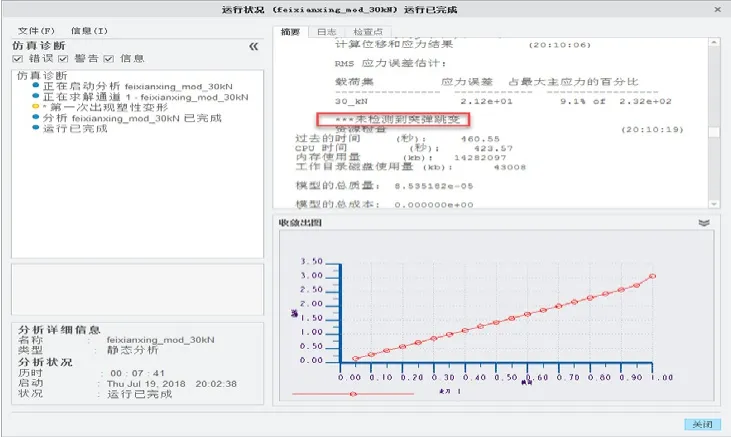
图13

（3）使用50kN载荷计算，检测到“突弹跳变”，分析收敛。摘要报告显示：在第15个时间步长，检测到可能的突弹跳变起点、终点（图14）。

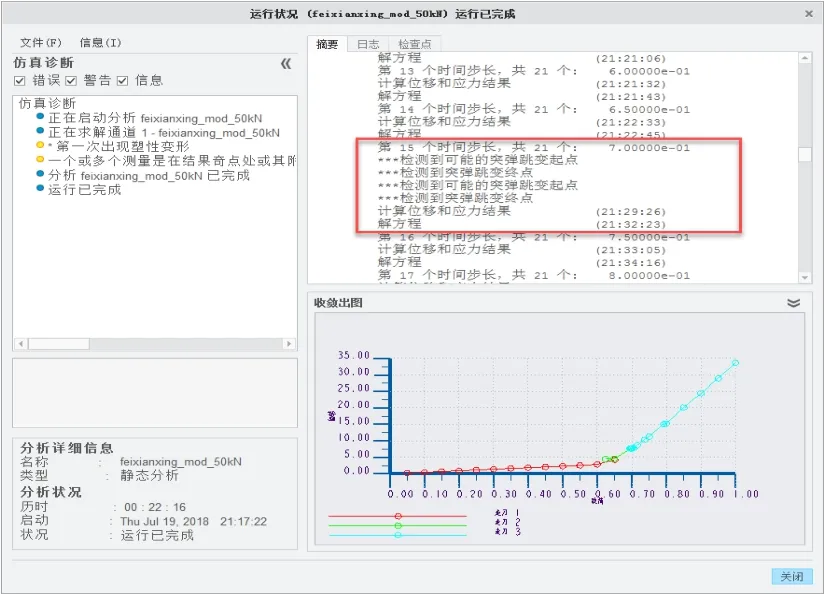
图14

6.查看分析运行结果

（1）从摘要报告可以看到下列信息（图15）：分析过程中出现塑性变形：0.4载荷历史时间；检测到突弹跳变的起点、终点：0.7载荷历史时间（0.6-0.8载荷历史时间段）；尽管选用快速检查、单通道自适应收敛方式，收敛图上出现多个通道。

图15

（2）通过塑性屈曲加载过程中最大等效应力——支反力的关系曲线、最大等效应力——载荷历史时间曲线可以看出，初始阶段在连杆一侧发生弹性变形（直线段），如图16所示。

在支反力为20kN（0.4载荷历史时间）时开始出现屈服，连杆上最大等效应力达到连杆材料的屈服极限180MPa，此时连杆开始出现塑性屈曲失稳，表现为随着外载荷增大，最大等效应力水平或出现跳动，即所谓的“吕德斯带”，开始塑性失稳。

再结合支反力和连杆最大位移之间的关系曲线、支反力——时间曲线，可以看出，在支反力达到35kN左右（0.7载荷历史时间，0.6-0.8载荷历史时间之间，30-40kN支反力之间）开始出现明显的突弹跳变现象，表现为支反力——位移曲线出现下降段。注意，缺陷较小的结构初始位移变形较小，在极值点突变，而初始缺陷较大的结构，载荷位移曲线较平滑。

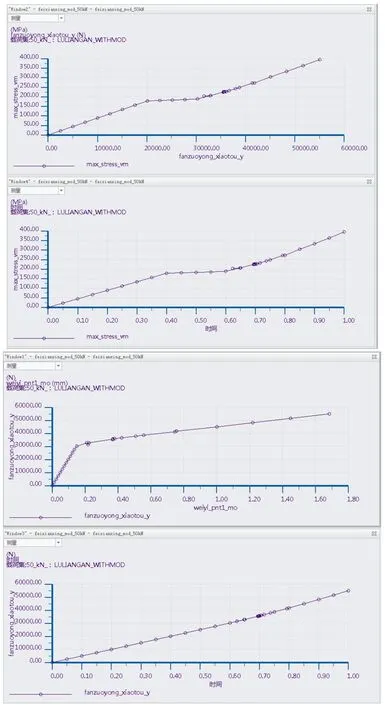
图16

综合上述分析，连杆力达到20kN时开始塑性失稳，35kN时出现突弹跳变，即后屈曲失稳，与线性屈曲分析计算的第一阶临界载荷1041kN相差甚远，以非线性失稳为准。连杆力最大为3.833kN，安全系数为6，稳定性特别好。