“探索图形”教学设计与评析
马伟鹏 王青巍
教学内容:人教版小学数学五年级数学实践课。
教学目标:
1.进一步认识和理解正方体特征。
2.通过观察、列表、想象等活动经历“找规律”的全过程,获得“化繁为简”的解决问题的经验,培养学生的空间想象力,让学生体会分类、数形结合、归纳、推理等数学思想。
3.在相互交流中,学会倾听他人的意见,提高小组合作的水平。
教学重、难点:发展学生的空间想象力,能通过实际操作,学会探索规律的归纳方法,学会解决复杂问题的“化繁为简”的思想方法。
教学流程:
一、引发问题,化繁为简
1.复习正方体的特征。
(1)师:同学们,很高兴能和大家一起上一节数学实践活动课,我们将共同探索图形当中的奥妙。(板书课题:探索图形。)
(2)师:请同学们看屏幕,这是什么图形?(课件出示棱长是1厘米的正方体。)
(3)师:正方体有哪些特征?
2.引出问题。
(1)师:如果用这样的棱长是1cm的小正方体拼成一个大正方体,它是由多少个小正方体组成的?你能试着拼摆出来吗?
(2) 师:请你仔细观察这个正方体,如果把这个大正方体的表面涂上红色,需要涂几个面?(课件演示:把大正方体6个面涂上红色。)
(3) 师:这些小正方体会有几个面被涂上红色?一个正方体有6个面,为什么只有3个面被涂上了红 色?
小结:那我可以理解成大正方体中,小正方体被涂色的面数与藏起来的面有关,如果某一个小正方体有4个面被藏起来了,则它就有2个面被涂上了红色。
(4) 师:请同学们想象一下,如果用更多的棱长是1厘米的小正方体拼成更大的正方体,并将这个大正方体表面图上红色,这些小正方体可能会有几个面被涂上红色?
(5) 师:假如,我用棱长是1cm的小正方体拼成棱长是10cm的正方体并将表面涂上红色,如果根据涂色的情况给这些小正方体分类,你想怎样分类?(分为四类:三面涂色的,两面涂色的,一面涂色的和没有涂色的。)
(6)师:每一类小正方体分别有多少个呢?如果请你来数一数,你有什么感觉?
(7)师:这个图形太复杂了,我们数起来不方便。怎样才能解决这个问题,你们有什么好办法吗?
小结:先研究简单的图形,发现规律之后,再利用规律去解决复杂的图形,这确实是很好的方法!
(设计意图:创设问题情境,大正方体中四类小正方体各有多少块?在解决这个问题过程中,促使学生积极主动思考解决问题的新方法,深刻体会化繁为简、探索规律解决问题的意义,让学生体会分类、归纳的数学思想。)
二、实践操作,探索规律
1.发现规律。
(1)师:你认为什么样的图形比较简单,我们容易找到答案?
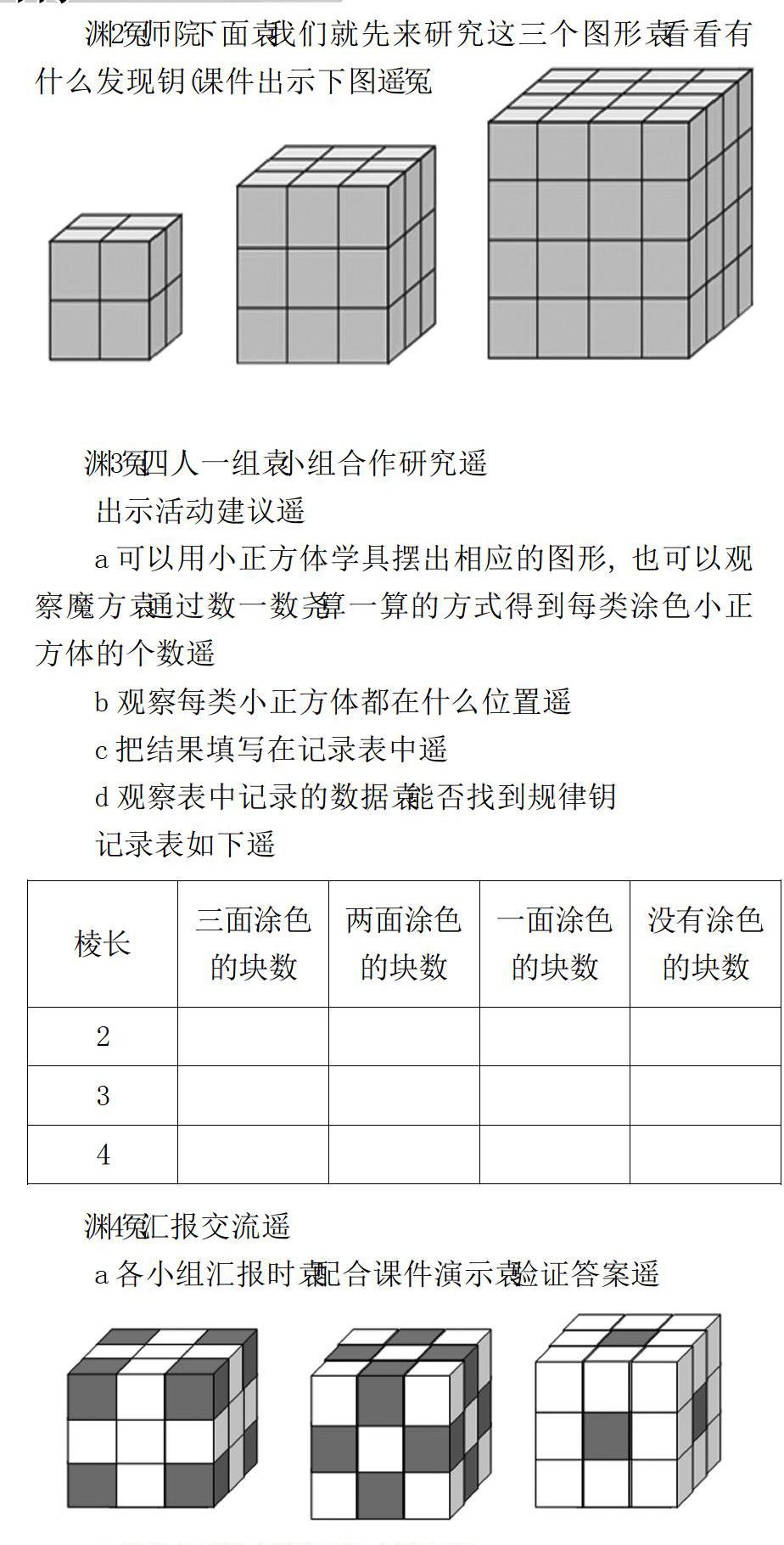
(2)师:下面,我们就先来研究这三个图形,看看有什么发现?(课件出示下圖。)
(3)四人一组,小组合作研究。
出示活动建议。
a可以用小正方体学具摆出相应的图形,也可以观察魔方,通过数一数、算一算的方式得到每类涂色小正方体的个数。
b观察每类小正方体都在什么位置。
c把结果填写在记录表中。
d观察表中记录的数据,能否找到规律?
记录表如下。
(4)汇报交流。
a各小组汇报时,配合课件演示,验证答案。
b学生汇报时教师适时提问:
请同学们想一想,在这些正方体中,你是通过什么方式得到每一类小正方体的个数的。
你们组是怎样算出没有涂色的块数的?(总块数—三面涂色的块数—两面涂色的块数—一面涂色的块数。)
c学生初步发现涂色的规律:
三面涂色的在正方体顶点的位置。
二面涂色的在正方体棱上除去两端的位置。
一面涂色的在正方体每个面除去周边一圈的位置。
没有涂色的在正方体里面除去表面一层的位置。
d师:请同学们想一想,三面涂色的小正方体为什么都在大正方体的顶点上?两面涂色的小正方体都出现在棱上?
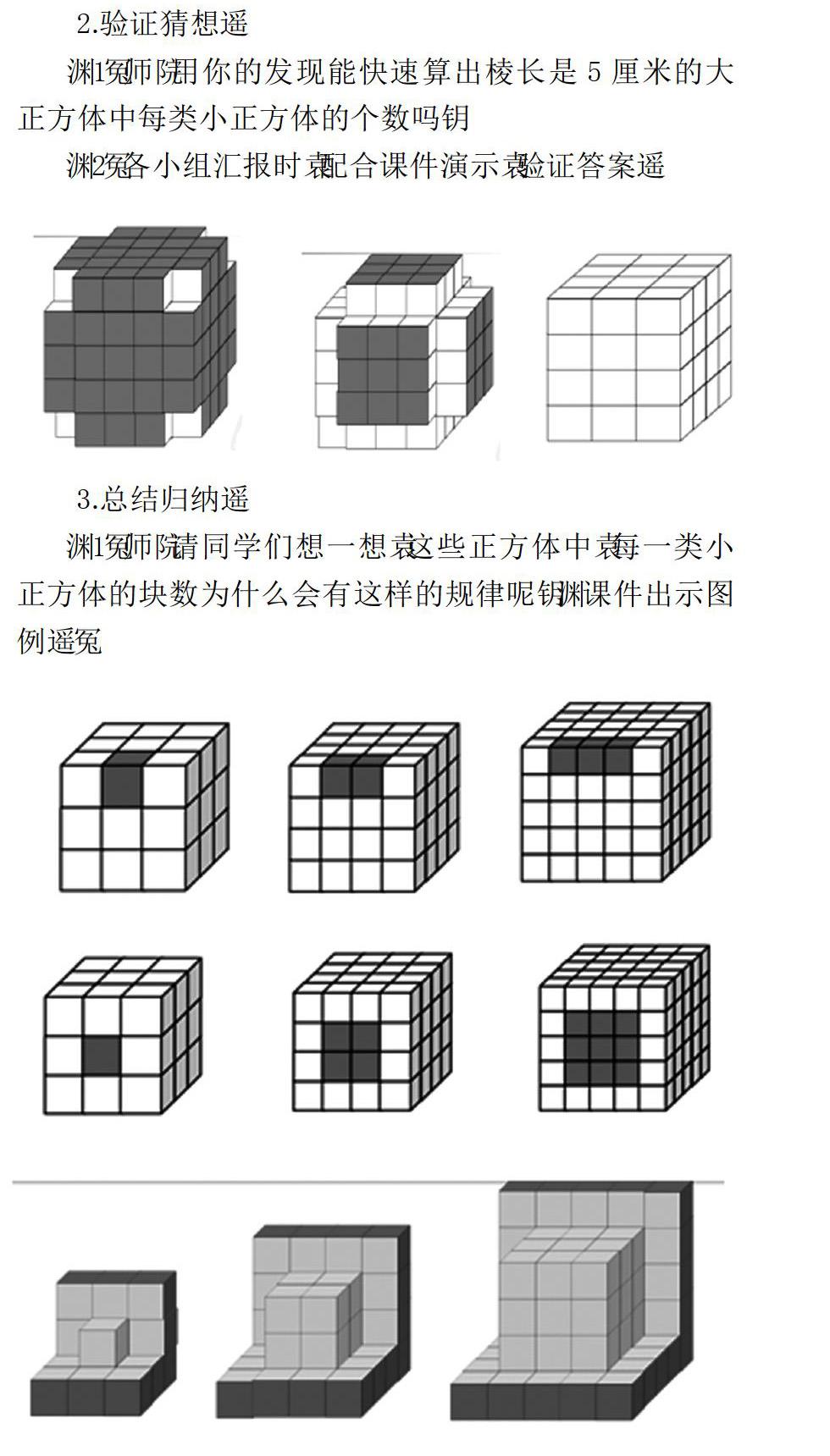
2.验证猜想。
(1)师:用你的发现能快速算出棱长是5厘米的大正方体中每类小正方体的个数吗?
(2)各小组汇报时,配合课件演示,验证答案。
3.总结归纳。
(1)师:请同学们想一想,这些正方体中,每一类小正方体的块数为什么会有这样的规律呢?(课件出示图例。)
(2)师生共同归纳:
a三面涂色的在正方体顶点的位置,因为正方体有8个顶点,所以都有8个;
b两面涂色的在正方体棱上除去两端的位置,因为正方体有12条棱,所以有(每条棱上小正方体块数 -2) ×12个;
c一面涂色的在正方体每个面除去周边一圈的位置,正方体有6个面, 所以(每条棱上小正方体块数 -2) ×(每条棱上小正方体块数-2) ×6个;
d没有涂色的在正方体里面除去表面一层的位置,所以有(每条棱上小正方体块数-2) ×(每条棱上小正方体块数-2) ×(每条棱上小正方体块数-2) 或者总块数—三面涂色的块数—两面涂色的块数— 一面涂色的块数。
4.应用规律。
师:现在能解决我们开始遇到的问题了吗?
课件出示:
三面涂色的:8个。
两面涂色的:(10-2)×12=96 (个)。
一面涂色的:(10-2)2×6=384 (个)。
没有面涂色的:(10-2)3 =512(个)。
(设计意图:引导学生经历发现规律——验证猜想——总结归纳——应用规律的过程,积累数学活动经验,让学生体会数形结合、归纳、推理的数学思想。)
三、巩固迁移,解决问题
1.师:如果请你数一数这样的几何体,你打算怎样做?(课件出示。)
2.学生尝试用探索规律的方法解决问题。
3.师:按这样的规律摆下去,第5个图形的结果是多少?第6个呢?第10个呢?
(设计意图:在学生初步学会探索规律的方法的基础上,通过引导学生尝试用这种方法解决新的问题,培养实际应用意识。)
四、课堂小结,提升方法
师:通过这节课的学习,你有什么收获?
小节:当我们遇到比较复杂的问题,解决起来有困难时,可以尝试先从简单的情况开始,看能否发现规律,再应用规律去解决复杂的问题,这是一种解决问题常用的思维方法。
反思:
“探索图形”是五年级的一节数学实践活动课,这就要求学生要有充分的动手操作实践,最好做到“在做中学,在学中做”。本节课学生在探索由小正方体拼成大正方体的涂色规律时,通过观察、列表、想象等活动经历“找规律”的全过程,获得“化繁为简”的解决问题的经验,经历了解决图形分类计数问题的思考过程,培养了空间想象力和推理能力,让学生体会分类、数形结合、归纳、推理、模型等数学思想。
通过教学我体会到在解空间观念比较强、又比较抽象的问题时,适时地运用多媒体可以使复杂的问题简单化,抽象的问题具体化,这样就有利于学生观察、分析、思考,它的直观性能突破视觉的限制,多角度地观察对象,并能够突出要点,有助于知识的理解和方法的掌握。我们在几何知识教学中,要充分利用点、线、面、体及它们的关系,发展学生的空间观念和提高解决实际问题的能力。
评析:
“探索图形”是一节数学活动课,是在学习正方体、长方体特征,计算表面积和体积的基础上进行探究的,这一部分内容,学生学习有难度,教师教学更有难度。因此马老师在教学中注重方法的引导,循循善诱,和学生一起探究知识,主要体现以下几点:
1. 注重运用化繁为简的策略解决问题。
在看到教材中的这个问题时,很多学生会感到很难,无从下手,马老师是这样引导学生解决的:首先,复习正方体的特征、点面棱数量及计算等,为学生解决问题储备基础知识;然后,将小正方体涂色情况进行分类,指导学生有序地思考、计算;接下来,由简单的2阶推到3阶、4阶,独立思考,交流合作;最后,在展示汇报中逐步发现规律,得出结论,再到后来的推理验证,去探究更复杂的几何体。教学中,马老师有一句话点拨得非常到位:“当我们遇到比较复杂的问题时,可以尝试先从简单的情况开始,看能否发现规律,再应用规律去解决复杂的问题,这是解决问题常用的思维方法,引导得法。”
2. 注重在实践活动中培养应用意识。
在现实生活中蕴含着大量与数量和图形有关的问题,学习数学就是让学生认识到这些问题可以抽象成数学问题,用数学方法解决。今天这个问题是给大正方体涂色,有涂3个面的,2个面的,1个面的,不涂色的。看到这儿,学生会感到很凌乱,但随着研究的深入,教师环环相扣的引导,学生惊喜地发现,原来它们与正方体的顶点、棱、面有着如此密切的联系,领会到运用数学知识可以顺利地解决现实中的复杂问题。这也是一个由具体到抽象的过程,在此过程中,学生的理性思维、空间观念也得到了一定的提升。
3. 注重在探究活动中渗透数学思想。
数学思想是数学知识和方法在更高层次上的抽象和概括,自課程改革以来,我们都重视在课堂上渗透数学思想。本节课上,马老师通过巧妙地设计,自然地融入了一些小学阶段重要的思想,比如:在研究小正方体有几个面涂色时应用了分类的思想;在把大正方体涂面的数量用算式表达出来时应用的是图形结合的思想;在研究2阶、3阶的基础上,推理探究4阶、5阶的情况,应用的是类比的思想,符号化思想、统计思想、极限思想、模型思想等,所以说这一节课,具有浓浓的数学味儿。
■ 编辑/魏继军

