关于高中立体几何学习心得的思考

吴润东

摘要：高中立体几何是初中平面几何学习的延续，也是高中数学学习的重点和难点部分。立体几何的学习，不仅要求学生具备良好的三维立体感知能力，还要求学生在做题中，能够灵活的运用各种定理。鉴于高中立体几何的难度，本文主要分享了立体几何学习的一些心得，提供一些个人认为较为实用的解题技巧。旨在为高中生的学习提供一些有价值的参考。

关键词：高中；立体几何；难点；技巧

前言：高中立体几何的考查点主要围绕基本概念、表面积、体积、点、线、面和与向量的关系等。单独学习这些模块时，并不会感觉到太大的难度，只需要运用一些基本定理，掌握一定的做题规律即可解题。但是，当立体几何知识点混在一起考查时，做题难度将会大幅度增加，需要运用到的知识内容也是多方面的。因此，本文重点分析高中立体几何知识混合类型题的解法[1]。

一、高中立体几何学习的重点和难点

对于不同的学生而言，在高中立体几何学习时，会产生不同的难点认识。例如，一些立体感较差的学生在学习三视图、求表面积或体积时比较吃力；一些数量关系成绩较差的学生，在学习向量模块时会感觉到难度；一些思维不够灵敏的学生，在一些需要做辅助线的题型中会遇到阻碍。因此，概括的说，高中立体几何的每一模块都是学习的难点，也是考查的重点。当然，由于大部分类型题与教师讲解的例题具有相同的解题步骤和方法，并不需要学生过多动脑。但是当部分模块的知识点混合在一起时，势必会增加解题的难度。例如，三视图和几何体表面积的结合，不仅要求学生通过三视图判断几何体的类型，还需要通过分析三视图中给出的数据，判断与几何体表面积求解公式相对应的值。因此，学生既要有一定的立体观察能力，还要记住几何体面积公式。当然，这种知识的结合是高中立体几何学习的一般内容，并不能称为难点[2]。

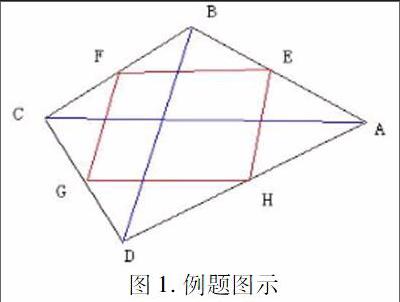
高中立体几何的学习难点可以通过一道具体的考查题目进行说明：已知四边形ABCD是空间四边形，E、F、G、H分别是边AB，BC，CD，DA的中点，求证（1）EFGH是平行四边形；（2）若BD=2√3，AC=2，EG=2。求异面直线AC、BD所成的角和EG、BD所成的角，图如1所示。这种题型是典型的立体几何难点考察题，解题时既要作多条辅助线，还要结合数形结合思想，通过数量关系挖掘图形中已给出的隐藏信息，还要掌握相关的定理和异面直线的性质。这种多知识点的混合考查是高中立体几何学习的难点，也是高考应试的重点。这种难题的特点是给出的图形较为简单，题干信息较少，求证部分会给出其它条件。

二、高中立体几何学习的解题技巧

学习立体几何，首先要熟练掌握相关的公式、定理和演绎定理等内容，以此为基础，本文主要通过一些具体的题型，说明不同题型的解题技巧。

1.空间几何体的三视图 空间几何体的三视图考查也分难度等级，基础题型如下：给出一个几何体的三视图，包括左视图、主视图和俯视图，具体如图2所示。在图中标注了解题所需要的尺寸，求解几何体的表面积。具体解题步骤如下：首先，根据三视图确定几何体为正三棱柱。其次，根据三视图确定原几何体及其有关数据，最后利用公式求解。

此类题的解题技巧如下：1.由三视图想象出几何体的形状；2.由相关数据得出几何体中的量，进而求出表面积或体积。掌握三视图是正确解决这类问题的关键，同时也体现了知识间的内在联系，是高考中常见的基础题型。

2.几何体的表面积和体积 当图形较为复杂时，几何体的表面积和体积求解是高中立体几何学习的难点。例如，给出四棱锥P-ABCD，底面ABCD是半径为R的圆的内接四边形，其BD是圆的直径，并给出∠ABD=60°，∠BDC=45°，△ADP∽△BAD，求线段PD的长；若PC=√11R，求三棱锥P-ABC的体积。解题思路如下：首先，根据条件得到AB、AD的长，再由相似三角形的性质求得PD的长。其次，证明PD⊥面ABCD，即PD为三棱锥的高，进而求得面积。

求几何体的体积问题，可以多角度、多方位地考虑问题，对三棱锥，等体积转化法是常用的方法，转换底面的原则是为了使高更加容易求得，常常把底面放在已知几何体的某一面上。求不规则几何体的体积，常用分割或补形的思想，将不规则几何体变化为规则几何体，易于求解。

3.线线关系类型题 平行关系类型题首先要记忆平行关系成立的一系列条件，共包含12个。在学习过程中要记忆所有平行关系成立的条件，从而保证在解题中能够引用正确的平行定理。具体而言，如果已知条件是“线面”平行，欲证的结论是“线线平行”，那么就将“线面平行”向“线线平行”转化，通常可以利用线面平行的性质定理，作辅助平面得到某条或某几条“面面的交线”来实现的这种转化。

垂直關系类型题，通常是利用线面垂直证明面面垂直。因此，首先要找到一个平面的垂线，并且这条垂线要在另一个平面内。通过面面垂直判定定理，得出最终的结论。

4.空间向量在立体几何中的应用 空间向量理论引入立体几何中，通常涉及到夹角、平行、垂直、距离等问题，其方法是不必添加繁杂的辅助线，只要建立适当的空间直角坐标系，写出相关点的坐标，利用向量运算解决立体几何问题。这样使问题坐标化、符号化、数量化，从而将推理问题完全转化为代数运算，降低了思维难度。

除了上述复杂题型以外，前文中所列举的难点题型，确实很难总结出具体的解题技巧。因为，偏难的题型对学生的思维能力要求较高，而思维的发展很难通过技巧实现。因此，掌握立体几何的基本知识点和定义，加强不同题型的训练，可以有效的提高立体几何成绩。

结论：综上所述，高中立体几何知识是高中数学的重点和难点，也是高考中最容易得分和丢分的模块。在学习时，一方面要重视基础知识的夯实，另一方面要增加训练量，在做题的过程中不断积累方法，掌握技巧。值得强调的是，技巧并不是凭空产生的，而是基于大量的练习。因此，如果想要提高立体几何学习成绩，一定要强化题本的练习。

参考文献：

[1]魏胤呈，刘丹. 高中立体几何解题研究[J]. 亚太教育，2016，（29）

[2]孙君海. 浅谈如何学好高中立体几何[J]. 学周刊，2015，（07）：109.

（作者单位：湖南省常德市芷兰实验学校 415000）