奇妙变换中点的坐标变化特征

李卓雅

平面直角坐标系是初中函数学习的基础，也是架设在数与形之间的桥梁，在我们初中数学中有着重要的作用和地位.在这一章节的学习中，给我留下最深刻印象的不是象限分类，不是位置确定，而是坐标系中那些奇妙的数对，以及这些数对所表示的点与点之间的两种变换.我结合图形，以具体的点为例，给大家介绍一下点的平移和点的翻折两大变换前后各点坐标之间的特殊关系吧！

点的平移：如图1，若点A的坐标为（1，2），将点A向上平移2个单位长度得到B，则点 B的坐标为（1，4），若将点A向下平移3个单位得到点C，则点C的坐标为（1，-1）.由以上操作，从特殊点到一般点，可以得到：若将一个点沿铅直方向上下平移，则其横坐标不变，纵坐标加减平移单位数量（纵坐标平移计算口诀为：上加下减）.若将点A向左平移4个单位长度得到D，则点D的坐标为（-3，2），若将点A向右平移5个单位得到点E，则点E的坐标为（6，2），由以上操作，从特殊点到一般点，可以得到：若将一个点沿水平方向左右平移，其纵坐标不变，横坐标加减平移单位数量（横坐标平移计算口诀为：左减右加）.

點的翻折：如图2，点A的坐标为（1，2），若将点A以y轴为对称轴翻折得到B，则点B的坐标为（-1，2），若将点A以x轴为对称轴翻折得到C，则点C的坐标为（1，-2）.由以上操作，从特殊点到一般点，若点A的坐标为（a，b），则它关于x轴的对称点C坐标为（a，-b），关于y轴的对称点B坐标为（-a，b）.此时，我们还可以看出点B与点C关于原点对称呢！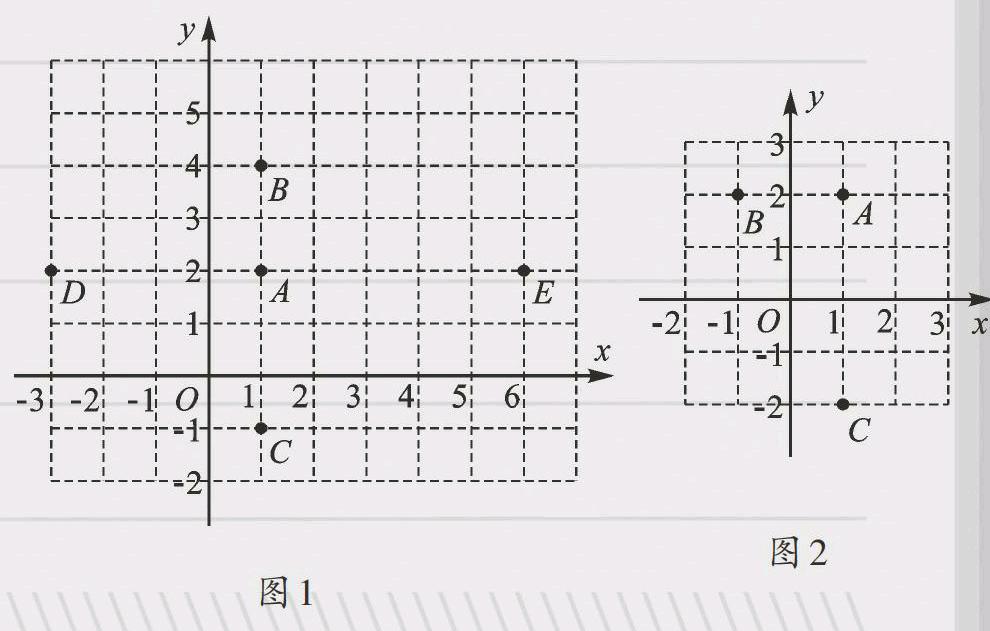

亲爱的同学们，你关注到这些奇妙的变换了吗？你能够理解这些奇妙变换中点的坐标变化特征吗？如果你能够理解，那我们不妨再来探索一下点A（a，b）关于直线x=m（m>a）或直线y=n（n>b）（如图3）的对称点的坐标吧！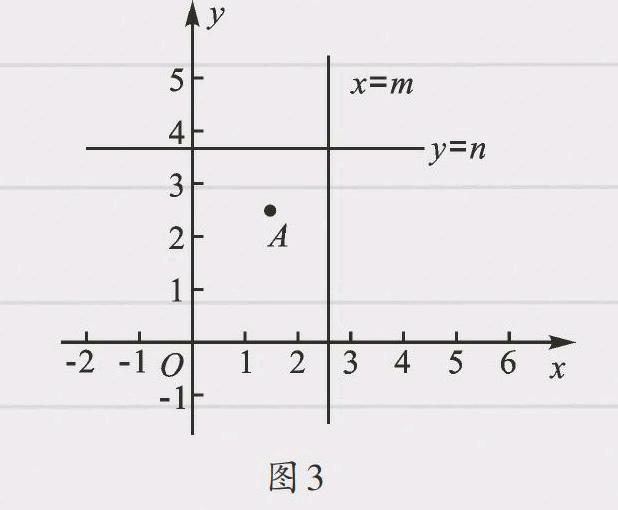

教师点评：你有着与众不同的智慧，总能够第一时间找到学习中的精华.点的坐标在平移与翻折中的特殊变化是本章节学习的重点，也是一个难点，你能够及时总结归纳并做拓展研究，老师非常开心，我为你感到骄傲！

（指导教师：范建兵）endprint