对称点的特殊与一般

叶智超

同学们，我们在课堂上研究了平面直角坐标系中任意一点关于坐标轴、原点的对称点的坐标特点，当我们把对称轴、对称中心进行适当平移后，这些对称点的坐标又会有什么样的变化呢？下面，让我们共同来研究.

请同学们思考这样一道题目：

1.在直角坐标系中，△ABC的三个顶点的坐标分别为A（-4，5），B（-5，2），C（-1，3）.

（1）△A0B0C0与△ABC关于y轴对称.在图1中画出△A0B0C0，并写出△A0B0C0三个顶点的坐标；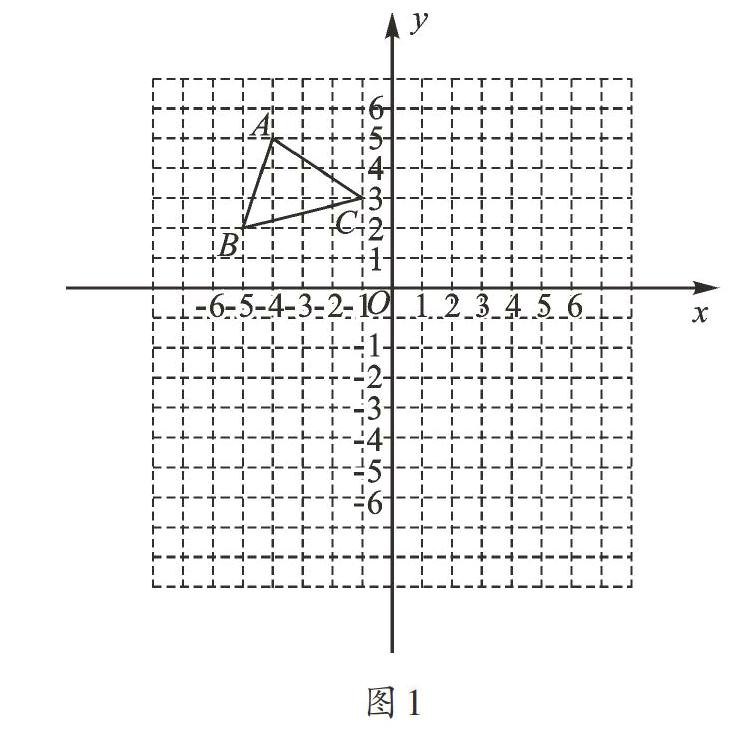

（2）观察图中对应点坐标之间的关系，写出直角坐标系中任意一点P（a，b）关于y轴的对称点的坐标：______.

【解析】（1）分别作出各点关于y轴的对称点，再顺次连接即可，图略，A0（4，5），B0（5，2），C0（1，3）；（2）（-a，b）.

【说明】本题主要考查在直角坐标系中根据轴对称的性质作图，以及图形的轴对称变换与点的坐标变化之间的关系.作关于y轴对称的图形是同学们平常接触过的问题，难度不大.

请同学们再观察下列两题：

2.在直角坐标系中，△ABC的三个顶点的坐标分别为A（-4，5），B（-5，2），C（-1，3）.

（1）直线l1经过点（1，0），并且与y轴平行， △A1B1C1与△ABC关于直线l1对称.在图2中画出△A1B1C1，并写出△A1B1C1三个顶点的坐标；

（2）比较图2中△A1B1C1与图1中△A0B0C0的位置关系，你发现了什么？

（3）写出直角坐标系中任意一点P（a，b）关于直线l1的对称点的坐标：______.

3.在直角坐标系中，△ABC的三个顶点的坐标分别为A（-4，5），B（-5，2），C（-1，3）.

（1）若直线l2经过点（2，0），并且与y轴平行，△A2B2C2与△ABC关于直线l2对称.在图3中画出△A2B2C2，并写出△A2B2C2三个顶点的坐标；

（2）比较图3中△A2B2C2与图1中△A0B0C0的位置关系，你发现了什么？

（3）写出直角坐标系中任意一点P（a，b）关于直线l2的对称点的坐标：______.

【解析】问题2中：（1）图略，A1（6，5），B1（7，2），C1（3，3）；（2）把△A0B0C0向右平移2个单位，得到△A1B1C1；（3）（-a+2，b）.问题3中：（1）图略，A2（8，5），B2（9，2），C2（5，3）；（2）把△A0B0C0向右平移4个单位，得到△A2B2C2；（3）（-a+4，b）.

下面请同学们仔细观察上述3个题目：

（1）你能发现对称的两个点的坐标有何关系吗？

（2）你能用语言描述你的发现并解释其中的道理吗？

（3）若直线l经过点（n，0）（n>0）并且与y轴平行，你能写出直角坐标系中任意一点P（a，b）关于直线l的对称点的坐标吗？

（4）当n<0时，情况又怎样呢？

（5）若直线l′经过点（0，m）并且与x轴平行，你能用上面所获得的活动经验研究直角坐标系中任意一点P（a，b）关于直线l′的对称点的坐标吗？

同学们，把对称轴改变后，这些对称点的坐标是否具有某种规律性？经过尝试，我们发现这种规律性是存在的，大家应该学着阐述对称轴的平移和对称图形的平移之间的关系，以及点的坐标的变化情况.当n>0时，点P（a，b）关于直线l的对称点的坐标是（-a+2n，b），当n<0时，坐标仍然满足上述规律.

我們在平时的数学学习中要学会对问题进行反思，把问题的条件或结论一般化，可能就会挖掘出更有价值的知识，形成对图形变换的整体认识.当然，再碰到较难问题时，我们也可先将条件或结论特殊化，去寻找特殊情形时的方法，然后再类比到所求问题中.

因此，同学们在学习与解题时，应多去感悟“特殊与一般”的数学思想，力争做一题会一类，掌握研究问题和解题的方法，提高学习能力.

练习：

1.在直角坐标系中， △ABC的位置如图4所示.

（1）先将△ABC向下平移2个单位后，再作该三角形（平移后的三角形）关于y轴成轴对称的图形，记为△A′B′C′，写出所作△A′B′C′各顶点的坐标；

（2）若先将△ABC向下平移m（m>0）个单位后，再作该三角形（平移后的三角形）关于直线l[直线l经过点（n，0），并且与y轴平行]成轴对称的图形，记为△A′′B′′C′′，你能写出△A′′B′′C′′的各顶点的坐标吗？

【答案】（1）图略，A′（-3， 2），B′（-2，-1），C′（-6，0）；（2）A′′（-3+2n，4-m），B′′（-2+2n，1-m），C′′（-6+2n，2-m ）.

（作者单位：南京航空航天大学附属初级中学）endprint