基于不确定性分析的页岩气单井SEC储量动态评估的一种方法——以CN区块Well-1井为例

李 舫 吴 娟 杨家静 汪 华 孙 挺

1.中国石油西南油气田分公司勘探开发研究院 2.中国石油大学（北京）

0 引言

“SEC”是美国证券交易委员会的简称，SEC储量即为上市储量，其内涵为“合理客观，剩余经济可采”，相当于国内的剩余经济可采储量。上市的油气生产经营公司每年须评估自身的SEC储量并向股民披露。SEC储量的品质及数量是油气公司在资本市场竞争力的体现。近年来，随着页岩气田的大力开发，越来越多的页岩气SEC储量走向国际资本市场，其评估方法也随之成为研究热点。页岩气属于非常规天然气，其SEC储量评估与常规气不同，是以单井为评估单元，采用动态法评估证实已开发储量，在单井证实已开发储量平均值基础上确定未开发区域单井证实未开发储量的大小。因此，单井SEC储量动态评估方法是页岩气SEC储量评估中的关键技术[1]。

页岩气藏大多采用水平井开发，单井产能受水力压力压裂等增产措施效果影响大[2]，由于在开发初期，生产资料有限，难以准确定量判断页岩气压裂水平井的关键参数，如水力裂缝长度、裂缝导流能力等[3-10]，加之页岩气储层水力裂缝数学描述及页岩气的储层中多尺度渗流理论尚不成熟[11-19]，因此，在开发初期预测页岩气井的产能并评估其SEC储量，相比常规天然气具有更大的不确定性，即SEC储量评估具有很大风险[20-29]，难以评判其经济性。

为应对这一难题，国外建立了的页岩气藏SEC储量不确定性评估方法体系，其技术路线为选取目标区块典型页岩气井，建立单井数值模型，预测单井最终总可采量（EUR）及SEC储量的概率分布，得到了相应的P90（采出概率不低于90%的值）、P50（采出概率不低于50%的值）、P10（采出概率不低于10的值）。这种方法相比确定性分析方法能直观反映评估结果的风险[30]，其本质上是通过概率方法进行足量模拟运算弥补勘探开发早期生产资料的欠缺和目前页岩气藏开发理论的不完备。除SEC储量评估外，这一方法体系在非常规油气开发方案优选、勘探开发项目经济性评价等领域均有很强的推广性。

本文借鉴国际通用的页岩气SEC储量不确定性评估方法，提出了一种操作性更强的单井最终总可采量（EUR）及SEC储量不确定性分析评估的方法。这种方法在勘探开发初期相关基础数据较少的情况下，对于页岩气SEC储量评估风险控制有重要意义。

1 方法原理与流程

1.1 基于贝叶斯定理的产量历史拟合及预测原理

贝叶斯定理是关于两个随机事件条件概率的定理，表达式为[31]：

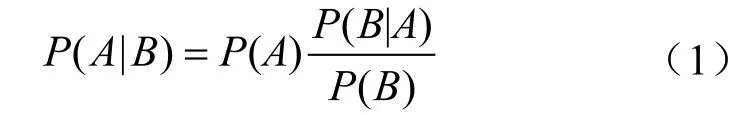
式中P(A|B)表示事件B成立时事件A成立的条件概率；P(B|A)表示事件A成立时事件B成立的条件概率；P(A)表示事件A成立的无条件概率；P(B)表示事件B成立的无条件概率。

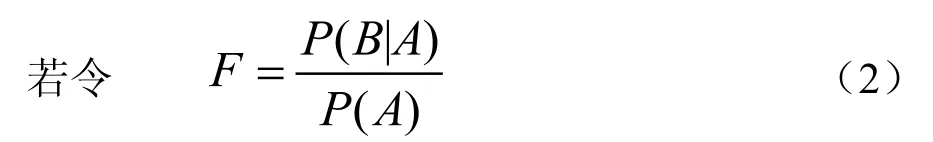
则式（1）可写为：

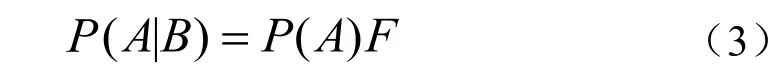
式（3）的含义为一个随机事件后验概率等于其先验概率与调整因子的乘积。这一理论用于单井数值模型产量历史拟合就是将事件A作为模型的拟合调整参数，B作为拟合的约束条件（产量历史数据、井底或井口压力实测数据等），P(A)表示产量历史拟合之前模型的参数分布，即参数先验概率分布，拟合的过程本质上是求取调整因子F的过程，P(A)F表征拟合完成后模型参数的后验概率分布。因此，基于贝叶斯定理的产量历史拟合及预测方法包含了单井数值模型参数先验概率分布到后验概率分布的过程，其与确定性的产量历史拟合方法基于最优化原理并追求拟合误差最小不同，基于贝叶斯公式的拟合方法是得到满足拟合精度的模型参数的概率分布，此分布包含了产量数据测量及数值模拟过程中的不确定性，能够在勘探开发初期，地质及生产资料有限的情况下得到相对准确的SEC储量影响关键因素的概率分布，进而得到SEC储量的概率分布，对开发初期SEC储量评估风险把控有重要价值。

1.2 基于拉丁超空间抽样的代理函数建立

目前基于贝叶斯定理的单井产量历史拟合及预测方法主要包括以下步骤：

（1）设定数值模型拟合参数的先验概率分布。

（2）采用特定的抽样方法对参数先验概率分布抽样，生成一定数量的候选单井数值模型。

（3）运行候选模型，根据设定的拟合精度筛选模型，同时调整模型参数的先验概率分布以得到后验概率分布。

（4）重复步骤（2）～（3），直到得到满足预设精度的模型参数后验概率分布。

（5）采用特定的抽样方法对参数后验概率分布抽样，取得足量模型，设定目标量（阶段累计产量、EUR等）预测的约束条件，运行模型得到目标量的概率分布。

Metropolis-Hasting MCMC是这类方法中的经典方法，它根据初始的候选模型和特定概率准则以一定随机步长抽取新的候选模型，比对初始模型与新模型参数拟合结果，若新模型参数后验概率大则替换初始的模型，经过大量这样的迭代运算最终得到满足设定精度的后验概率分布。

以Metropolis-Hasting MCMC方法为代表的贝叶斯产量历史拟合及预测方法用于单井数值模拟需要大量耗时的运算，因为这类方法需要上千次迭代才能转换到目标分布，每次迭代需要一系列费时的数值模拟运算。此外，这类方法的样本选取率通常很低，大量候选样本在迭代运算过程中被排除，这意味着大量耗时的数值模拟运算被浪费了[30]。

为克服这一缺点，在较少运算次数的条件下得到模型参数的后验概率分布及预测目标量的概率分布，本文运用拉丁超立方抽样方法（Latin hypercube sampling）对模型关键参数的先验概率分布进行抽样并组合生成一系列的单井数值模型，模型数量不小于能够表征关键参数实际分布的最小数量，称其为样本模型。运行样本模型，再根据设置的产量历史拟合精度选取模型，统计被选中的模型关键参数分布即可得到相关参数（孔隙度、基质渗透率等）的后验概率分布，然后设置预测目标量（累计产气量、最终总可采量等）的预测约束条件并运行模型得到预测值，最后利用这些预测值建立代理函数，即单井模型关键参数与预测目标量之间的函数关系式，具体步骤如下：

（1）设定单井数值模型的拟合参数及分布范围即关键参数的先验概率分布。

（2）设定抽样次数，利用拉丁超立方抽样方法对参数先验概率分布进行抽样，得到样本模型。

（3）运行样本模型进行产量或压力拟合，选取满足拟合精度的模型，将其中一部分作为训练样本，另一部分作为验证样本。

（4）对训练样本及验证样本的相关拟合参数（如基质孔隙度、基质渗透率、水力裂缝半长等）进行统计得到其概率分布，作为关键参数的后验概率分布。

（5）设定单井最终总可采量（EUR）预测条件（定压、定产量生产或计划关井等），产量预测的截止点为经济极限产量。运行训练样本及验证样本模型得到预测值，经济极限产量计算式为：

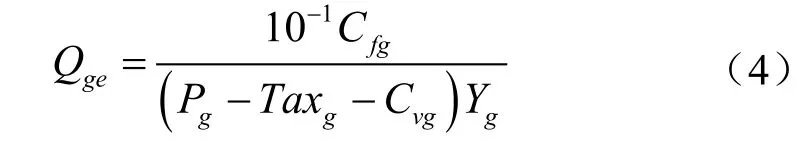
式中Qge表示井口天然气经济极限产量，108m3/年；Cfg表示固定成本，104元/年；Pg表示不含增值税气价，元/103m3；Taxg表示单位商品气税费，元/103m3；Cvg表示可变成本，元 /103m3；Yg表示天然气商品率，小数。

（6）确定代理函数类型（线性函数、单层径向神经网络、变差函数等），利用训练样本建立单井最终总可采量（EUR）的代理函数，即关键参数与单井最终总可采量的函数关系式。

（7）利用验证样本的单井最终总可采量检验代理函数预测精度，若不满足预设精度，重复步骤（2）～（6）。

1.3 基于蒙特卡洛方法的单井SEC储量预测

在建立代理函数后，根据关键拟合参数后验概率分布，对代理函数进行蒙特卡罗模拟，得到单井最终总可采量（EUR）的累积概率分布，从中读取P90、P50、P10的值，再分别减去单井目前的累计产量即可得到对应的SEC储量P90、P50、P10值，也可利用EUR与SEC储量的关系，根据EUR概率分布直接得到SEC储量概率分布。值得注意的是，蒙特卡罗模拟的次数需要足量，以得到平滑的EUR累积概率分布图。

2 实例分析

2.1 页岩气单井模型建立

选择四川盆地CN区块Well-1井建立其单井数值模型（图1），水平段长度1 000 m，模型为双孔双渗模型，渗流通道为水力裂缝，水力裂缝形态为“双翼缝”，裂缝完全贯穿储层，裂缝网格进行加密处理。基质为气体储集空间，基质与基质之间，基质与裂缝之间均存在流动，气体在基质中的解吸附效应采用Langmuir等温吸附模型描述，水相仅存在于裂缝中，考虑毛细管力作用、气体在裂缝中渗流的非达西效应以及气体在基质中的拟稳态扩散效应。相关气藏参数及数值模型参数如表1及表2所示。

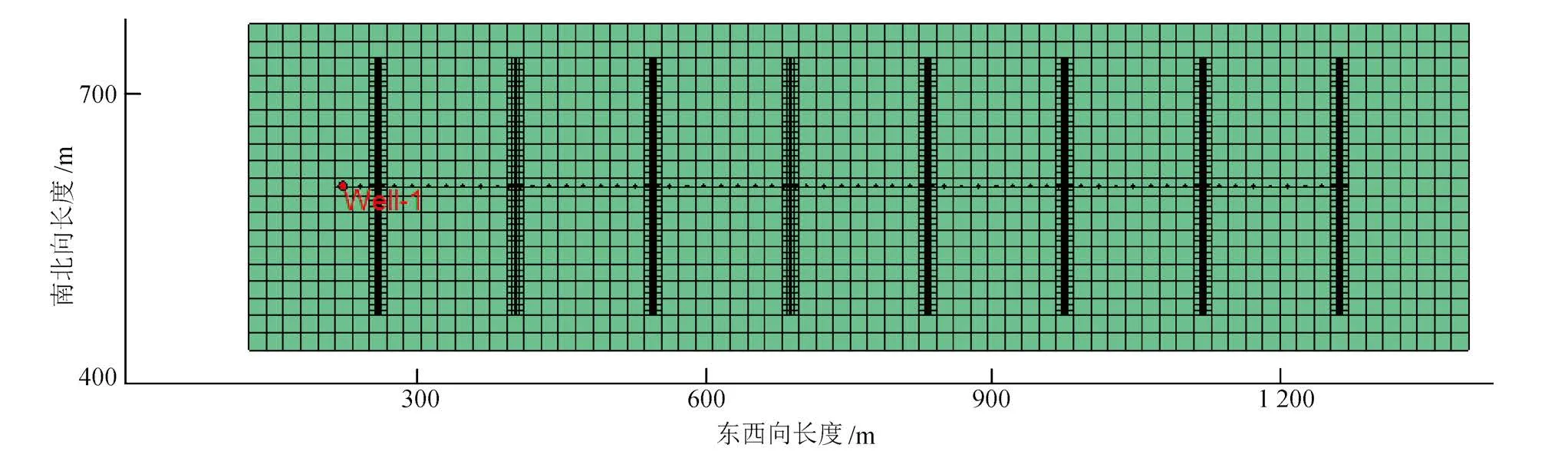
图1 Well-1井数值模型平面图

表1 CN区块页岩气藏参数表

表2 Well-1井数值模型主要参数表

表2中的值为数值模型的初始值，研究表明，相比常规气井，页岩气井的水力裂缝长度、水力裂缝导流能力、基质孔隙度与基质渗透率具有更大的不确定性和随机性，是单井数值建模的关键参数，也是产量历史拟合及预测的关键参数[3-5]，因此将水力裂缝长度、水力裂缝渗透率、基质孔隙度、基质渗透率设定为随机变量，进行不确定性分析。

2.2 产量历史拟合关键参数先验概率分布设定

根据CN区块页岩气探明储量报告研究成果及已知的储层非均质性，设定模型基质孔隙度先验分布为1%～8%之间的均匀分布。由该区块岩心样品统计结果，设定基质渗透率分布为1.00×10－4mD～ 1.00×10－3mD之间的均匀分布。由于缺少导流能力实验数据，根据该井组压裂设计主要参数推算出水力缝导流能力分布为0.007 925 mD·m～39.624 mD·m之间的均匀分布。根据该井区压裂设计及压后微地震监测结果，水力裂缝半长为50 m ～200 m。同时，运用归一化产量与时间的关系图版诊断得到该井的裂缝半长为53 m～138 m，由此设定水力裂缝半长分布为50 m～140 m之间的均匀分布。

2.3 训练样本模型选取及关键参数后验概率分布统计

运用拉丁超立方抽样方法（Latin hypercube sampling）对上述4个关键参数进行76次抽样，用抽样得到的参数组合依次替换初始模型的相关参数，生成76个样本模型，即采用这76个离散的参数组合代表参数本身在空间的连续分布。

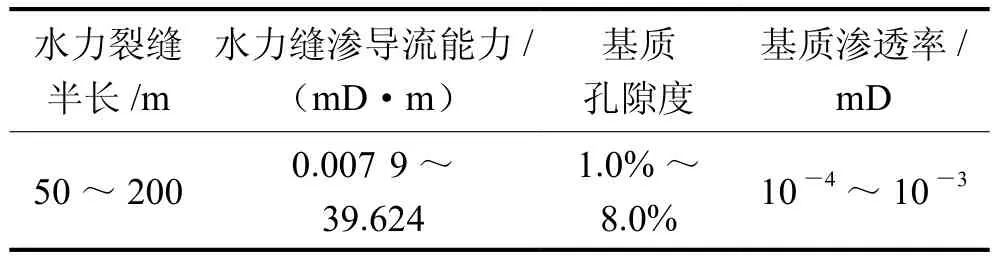
表3 Well-1井数值模型关键参数先验分布

Well-1井产量历史时间2014年5月1日至2017年12月1日，按此时间段设定该井产量历史拟合起点与终点，2017年10月30日之后产量预测条件为：井口最小油压为5 MPa，预测截止点为经济极限产量3 000方/天，即预测产量低于该值，则停止预测并求取投产初期至截止点的累计产量，即可得到对应的单井最终总可采量（EUR）。运行上述76个模型，得到产量历史拟合及预测结果（图2）。

以产量历史拟合总相对误差小于10%为筛选条件，从图2中选择满足精度的模型27个，对其4个拟合关键参数概率分布进行统计，得到4个参数的后验概率分布（图3），统计结果表明：4个参数的后验概率分布均为截断正态分布，不再是最初设定的均匀分布，其中，水力裂缝半长的分布范围是54～126 m，标准差26.83，水力裂缝导流能力分布范围是6～39 mD·m，标准差15.15，基质孔隙度分布范围是1.0～8.0%，标准差2.7，基质渗透率分布范围是0.000 1～0.001 0 mD，标准差0.0003（图3）。

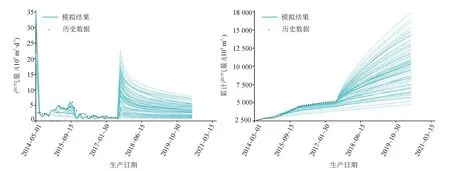
图2 样本模型产量、累计产量历史拟合及预测结果

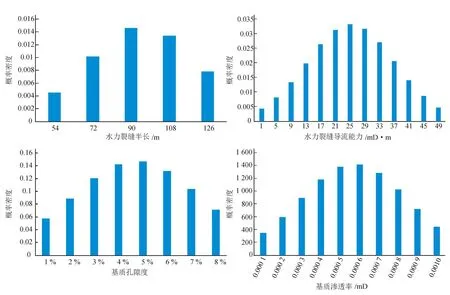
图3 4个关键参数的后验概率分布

2.4 单井最终总可采（EUR）代理函数建立

设定代理函数的类型为普通克里金函数，从上述27个样本模型中随机选取23个作为训练样本，其余4个作为验证样本，模型关键拟合参数作为自变量，所预测的最终总可采量（EUR）作为因变量，经过迭代运算得到代理函数相关参数：变差函数基台值为1.35×1017，变差函数指数为1.5，其余参数如表4所示。

代理函数对Well-1的最终总可采量（EUR）预测结果与训练样本模型、验证样本模型模拟结果对比情况（图4）叙述如下：

图4中蓝色的点表示训练样本，红色点表示验证样本，横坐标为代理函数计算EUR值，纵坐标为样本数值模型模拟预测值，易见，训练样本EUR呈45度斜线，验证样本EUR几乎落在这条线上（误差小于5%），说明代理函数计算EUR精度高，能够用于下一步的EUR及SEC储量不确定性分析。

表4 代理函数参数权重

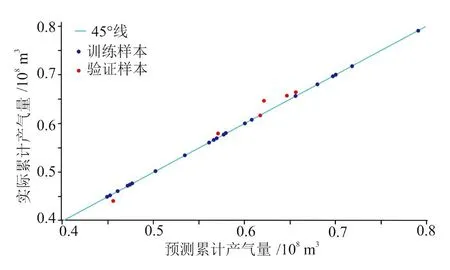
图4 代理函数计算结果与训练样本模型、验证样本模型模拟结果对比

2.5 基于蒙特卡罗的单井EUR及SEC储量不确定性分析

利用上一步建立的代理函数及4个拟合关键参数的后验概率分布，进行蒙特卡洛模拟，经过65000次运算得到Well-1井EUR的累积概率分布（CDF），如图5所示。

从图5可见Well-1的EUR概率分布为截断正态分布，累计概率为90%的值（P90，储量采出概率不小于90%）为0.50×108m3，累计概率为50%的值（P50，储量采出概率不小于50%）为0.61×108m3，累计概率为10%的值（P10，储量采出概率不小于 10%）为 0.75×108m3。

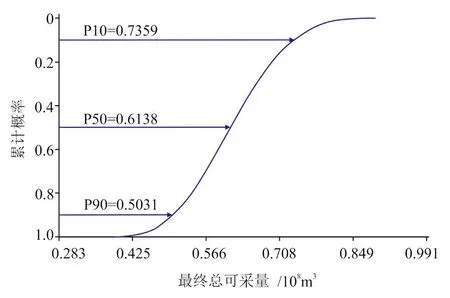
图5 Well-1井最终总可采量（EUR）累计概率分布图

利用EUR的P90值减去Well-1井之前的累计产气量0.35×108m3，得到对应的SEC储量P10值为 0.39×108m3，同理，SEC 储量 P50 值为 0.26×108m3，P90值为 0.15×108m3。该井 SEC 储量的概率分布可由EUR概率分布直接得到，不再详述。

值得注意的是，在引入代理函数和蒙特卡罗模拟后，仅需数十次单井数值模拟运算，即可得到该井最终总可采量及SEC储量的概率分布，该实例运用普通PC机花费20小时左右可完成，相比前文所述的动辄花费上百小时需要高端工作站甚至大型计算机群的不确定性评估方法，有很强的可操作性，节省了大量的人力、物力，是对目前国际主流页岩气储量不确定性评估方法流程的改进和创新应用。

该方法在节省运算成本的前提下也保障了计算精度，国际权威储量评估机构认为Well-1井不确定性计算结果考虑了页岩气单井SEC储量的主要影响因素，技术路线清晰，计算结果能代表目前CN区块页岩气储层改造工艺水平。国际储量评估机构的计算结果与本计算结果对比如下。

可见，本文结果与国际评估机构计算结果相差仅为3%。本计算方法实用性强，具有推广性。

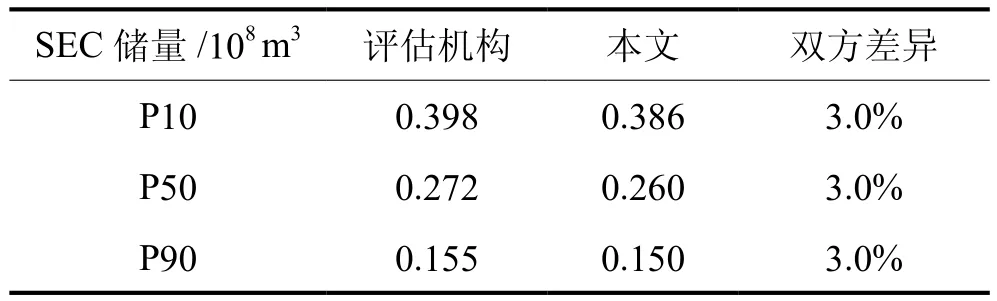
表5 Well-1井SEC储量计算结果对比

2.6 不确定性方法与确定性方法对比

上述不确定性方法的分析结果一方面能对已有的确定性评估结果进行风险评价，另一方面能为新的确定性评估参数选取提供理论依据。仍以Well-1井为例，采用双曲递减模型进行气井产量历史拟合预测，从图6可见，双曲递减模型的递减指数b是预测关键参数，在产量历史拟合精度相当的条件下，选取的b值不同，预测结果不同，且预测结果的风险难以直观表示，若将其与不确定性评估结果对比，则可知：当递减指数b取1.0时得到的EUR值即是P10值，若b取0.8可得到P50的值，若b取0.5时得到的是P90的值。SEC储量定义为采出概率大于等于90%且经济的储量，因此，b取0.5最合适，若仅靠经验选取b值，计算得到的Well-1井的SEC储量值可能偏大，进而导致对开发前景和投资回报的误判。

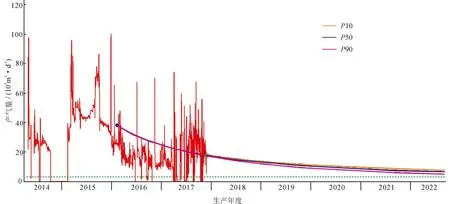
图6 Well-1井最终总可采量（EUR）确定性方法预测预测结果与概率

目前，本方法已经在CN区块运用30井次，得到以下认识：（1）该区块典型气井SEC储量P90值为0.5～1.3亿方，（2）SEC储量P90值对应的递减指数（b）为0.5～1.0。上述两点认识均得到国际储量评估机构认可，为CN区块页岩气SEC储量评估提供了技术支撑，为CN区块页岩气储量资产走向国际资本市场奠定了基础。

3 结论

1）不确定性方法能综合考虑页岩气勘探开发中的不确定性因素，得到特定井的SEC储量概率分布，直接反映储量评估风险，相较确定性方法更适合页岩气SEC储量的评估。

2）笔者所述的评估方法对国际通用方法流程进行了创新，保障计算精度的同时节省了运算成本，增强了这类方法的实用性。

3）目前该方法已在CN区块推广应用，评估典型页岩气井30井次，所得到的评估结果及认识均得到国际权威储量评估机构认可，运用前景广阔。