数列经典题型突破

■河南省商丘市第一高级中学 周文辉

数列是高考数学的重点与热点内容,也是必考内容,高考关于数列考点的命题,主要有以下几个方面：(1)对数列的基本性质、基本运算的考查,经常以选择、填空题的形式出现,属于容易题;(2)由递推公式求数列的通项公式,进而求数列的前n项和,考查化归思想与几种常见数列求和类型的熟练程度,常以解答题的形式出现,属于中档题;(3)数列与其他知识的综合,如数列与函数、方程、不等式、三角函数、解析几何的结合,以小题压轴题的形式出现,其中以数列与函数、不等式的综合最为常见。

题型一：由递推公式求通项公式

解决这一类型问题的核心思想是将非等差、等比数列通过构造的方式,转化为等差、等比数列后再进行求解。

1a.n+1=pan+q类型,求解此类型的方法是将原式化为an+1+m=p(an+m),利用两式的等价性求出m=。

例1 已知a1=1,an+1=2an+1,求an的通项公式。

解析：an+1+1=2(an+1),令bn=an+1,则bn为等比数列,可求其通项公式bn=b1=2,bn=b1×2n-1=2n,所以an=2n-1。

2.an+1=pan+qn类型,此类型的方法是将原式化利用累加法可求。

例2 已知a1=1,an+1=2an+3n+1,求an的通项公式。

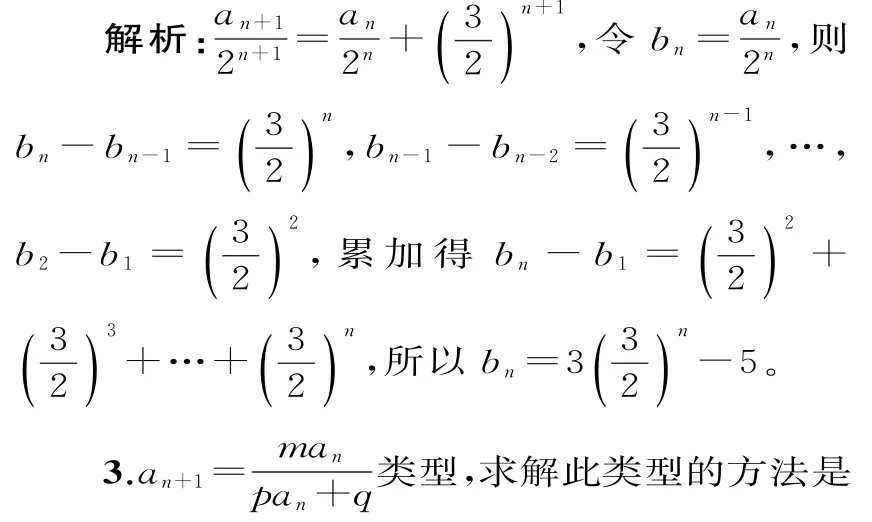
题型二：数列最值问题

解决这一类型问题常采用单调性方法,即判定数列的单调性,进而求出最值;还可以采用注意采用这种方法求出的结果需要和a1进行比较。

题型三：数列前n项和性质的深层理解

例5 已知an,bn是等差数列,Sn,Tn为其前n项和

例6 已知an,bn是等比数列,Sn,Tn为其前n项和