一种双调制率调频引信抗DRFM干扰方法
王 哲, 闫 岩, 金 钊, 程思敏
(北京遥感设备研究所,北京100854)
0 引言
调频引信是一种发射信号频率按调制信号规律变化的无线电引信,利用发射信号和回波信号频率差值与弹目距离的对应关系,实现引信定距功能[1]。相对于连续波多普勒引信,具有定距精度高、抗干扰性能好等特点,且算法复杂度低,容易在硬件平台上实现[2],在弹药装备中得到了广泛应用。
电子干扰对调频引信的战场生存能力构成了严重威胁[3-4]。基于数字射频存储 (DRFM)的干扰机可以准确地存储、重构和转发调频引信的发射信号,从而实现假目标欺骗干扰。近年来,抗DRFM干扰研究的一个重要分支是发射波形的设计,包括脉冲压缩[5]、频率捷变[6]、脉冲多样性[7]、脉冲重复周期跳变等方法[8]。频率捷变系统可以在保留信号处理设计的基础上,仅通过改变前端设计获得良好的抗干扰效果,在各种引信体制中已得到了广泛应用。在工程实现方面,还需要克服高次谐波的影响。随着跳频点数的增加,系统信噪比会进一步降低。
本文基于发射波形去周期化设计的抗干扰思路,提出一种基于双调制频率跳变的调频引信抗DRFM干扰方法。这种方法可以改善现有调频体制引信的距离模糊特性,从而抑制存储转发干扰的影响。本文以理论分析为基础,介绍了半实物仿真测试结果,验证了该方法的可行性与有效性。
1 DRFM干扰作用下调频引信失效机理
如前所述,调频引信发射信号的频率是时间的函数,发射信号通常采用周期调制,差频信号频谱以调制频率整数倍的各次谐波形式分布,利用某次谐波能量的最大值与距离的对应关系,可实现引信定距功能。图1为典型单通道调频多普勒引信原理框图。
调制器产生频率为fm的三角波调制信号对振荡器进行线性调频,目标反射信号被收发共用天线接收,经环形器后与本振信号混频得到差频信号,边带放大器选取mfm±fD频率成分进行二次混频和包络检波,得到幅度随距离变化的多普勒信号包络送至执行级进行起爆判决。
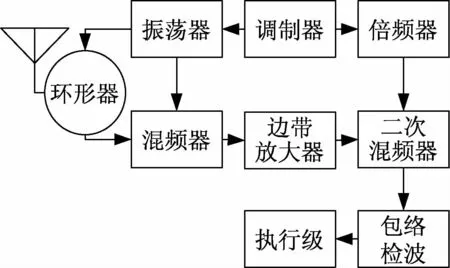
图1 单通道调频多普勒引信原理框图
以对地连续波调频引信为例,DRFM干扰模型示意图如图2所示。干扰机通过延迟转发引信发射信号,在引信接收端形成距离假目标,导致引信提前启动。

图2 DRFM干扰模型示意图
已知调频引信发射信号为s(t),DRFM干扰机对侦收到的引信发射信号进行存储,并在附加延迟时间后转发,干扰信号sj(t)可以表示为
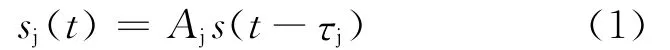
式中:Aj为DRFM干扰机发射干扰信号幅度;τj为干扰信号延迟时间,τj=2Rj/c+τj0,它由信号在空间中的传播时间和干扰机附加延迟时间τj0组成;Rj为干扰机到引信的距离;c为光速。
目标回波信号sr(t)可以表示为

式中:Aj为目标回波信号的幅度;τd为目标回波延迟时间,τd=2Rd/c;Rd为弹目距离,且满足引信的起爆距离。根据DRFM干扰模型,一般情况下Rj远大于Rd,相应的延迟时间τj也远大于τd。虽然干扰信号可以在形式上高度近似目标回波信号,但τj在小于调制周期Tm内,无法导致引信接收端输出满足起爆距离的假目标信号。因此DRFM干扰机成功干扰调频引信的必要条件是τj至少要大于一个Tm,即满足以下条件:

式中:N*为正整数。DRFM干扰机在获取Rj的前提下,通过合理设置τj0,使得式(3)成立,从而利用s(t)的周期调制带来的距离模糊实现欺骗干扰,使引信在距离目标很远的位置探测到满足起爆距离的假目标而提前启动。
2 调频引信抗DRFM干扰设计
根据上述失效机理,可以将发射波形去周期化设计作为调频引信抗DRFM干扰研究的基本思路。本文提出一种双调制频率随机跳变的三角波线性调频发射波形,采用m序列作为控制fm跳变的伪随机码,实现发射波形去周期化,并设计基于FFT的谐波时序检测方法完成目标判别。图3为抗DRFM干扰调频引信系统原理框图。

图3 抗DRFM干扰调频引信系统原理框图
图3 中调频引信系统与传统方案主要有两点差异:其一,采用双调制率调制器产生复合调制波形;其二,采用基于FFT的谐波时序检测方法处理差频信号。
2.1 双调制频率抗DRFM干扰波形设计
已知传统三角波线性调频引信的差频信号频率fi与弹目距离R之间的关系由调频测距公式确定,即
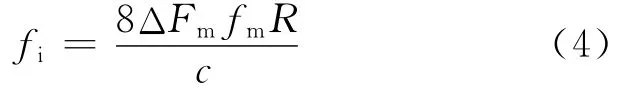
为了提高调频引信抗DRFM干扰性能,可以改变调制参数实现发射波形的去周期化,可变参数包括载频f0、调制频率fm和半调制频偏ΔFm。
通过改变f0可以在保持原有信号处理方法不变的同时,取得比较理想的抗干扰效果[9]。但发射信号频率随时间非连续变化,且存在大幅度跳变,对VCO的响应性能要求很高。同时,由于差频信号在时频域存在较大“毛刺”,进而会带来高次谐波,增加了信号处理的难度。
采用变fm实现发射波形去周期化,由式(6)可知,单一改变fm或ΔFm会导致fi与R不再满足线性对应关系,给引信定距带来不便。本文设计ΔFm在fm跳变的同时也发生跳变,但调制斜率β=4ΔFmfm始终不变,从而保持fi与R的线性对应关系。
图4为本文设计双调制频率三角波线性调频发射信号频率随时间变化曲线,调制周期Tm=1/fm在两种取值之间随机跳变,且Tm1=2Tm2;ΔFm也存在两种取值,且满足ΔFm1=2ΔFm2。调制参数的跳变由二进制m序列生成的伪随机码控制。为便于工程实现,取码元宽度Tc=Tm1,伪随机码周期Tr=PTc,P为伪随机序列长度。假设调频信号初始相位φ0=0,载频为f0,信号幅度为At,则发射信号在一个调制周期[-Tm1/2,+Tm1/2]内可以表示为

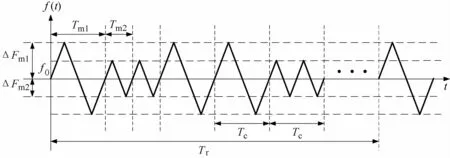
图4 双调制频率三角波线性调频发射信号时频图
三角波线性调频信号u1(t)可以表示为

同理,可得到Tm2周期内发射信号及其对应的调频信号表达式分别为v2(t)、u2(t)。
m序列产生器一般的数学表达式为
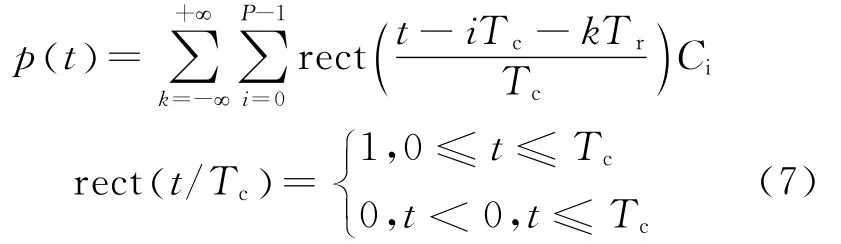
式中:Ci={1,0}为二进制m序列,通过N位线性移位寄存器产生,伪随机序列长度P=2N-1。假设Ci,n表示对m序列Ci进行逻辑非运算的结果,代入可得到其反码表达式为pn(t)。
综上所述,可得双调制频率三角波线性调频发射信号为

由式(8)可知,发射信号由调制参数不同的两种调频信号组成,分别在m序列及其反码的控制下随机跳变。式中两项调频信号存在半个周期的平移,目的是使叠加的发射信号瞬时频率随时间连续变化。
2.2 抗DRFM干扰系统差频信号分析
双调制频率调频引信差频信号的频率随时间变化关系如图5,图中上半部分的实线表示发射信号,虚线表示目标回波信号;τ=2R/c表示目标回波延迟时间。下半部分为差频信号频率fi随时间变化的曲线。

图5 目标回波作用下差频信号时频图
由图5可见,由于β=4ΔFmfm不变,fi的频率成分集中且与R线性对应。不同fm差频信号的不规则区具有不同的分布特点,且fi变化的周期等于Tm,即fi变化规律也在m序列的控制下,在两种状态之间随机跳变。首先对图5中码元Tc1对应的Tm1内差频信号作傅里叶变换,得到频率间隔为fm1的离散谱表达式[10]为

式中:m 为谐波次数;α1(m,τ)为傅里叶系数表达式,具体形式如式(10)所示。差频信号中m次谐波傅里叶系数α1(m,τ)包含两个sinc函数项,其中第二项的自变量取值范围远离包络主瓣而可以忽略。差频信号的m次谐波幅度随延迟时间τ变化具有类似sinc函数包络的形式,主瓣宽度 Δτ1=1/ΔFm1,且在 m=8ΔFm1R/c时出现峰值。

对于图5,Tc2内的差频信号只要将式(9)与式(10)中的Tm1、ΔFm1替换成Tm2、ΔFm2即可得到相应表达式,且差频信号的m次谐波幅度随延迟时间τ的变化规律相同,差异在于选定的m次谐波频率mfm2=2mfm1,且sinc函数包络主瓣宽度Δτ2=2Δτ1。
下面讨论弹目存在相对运动时,谐波幅度随时间的变化关系。假设引信相对于目标作匀速直线运动且相对速度为vR,弹目初始距离为R0,则目标回波延迟时间为τ=2(R0-vRt)/c,代入式(10)中得到Tc1、Tc2内m次谐波幅度随时间变化的表达式分别为α1,D(m,t)、α2,D(m,t)。相当于对原式进行自变量的平移和尺度变换,因此包络仍具备sinc函数的形式。另外由于存在相对运动,各次谐波幅度会受到多普勒频率fD的幅度调制[11]。结合m序列伪随机码及其反码的表达式p(t)、pn(t),可以得到弹目接近过程中,差频信号中m次谐波幅度随时间变化的表达式为
图6为差频信号m次谐波幅度α(m,t)随时间变化的关系,近似sinc函数包络,不规则部分是由两种主瓣宽度不同的sinc包络合成导致的。随着弹目距离不断减小,从高次到低次谐波信号会依次出现峰值,可以利用各次谐波的时序性作为目标判别依据。

图6 m次谐波幅度随时间的变化
图7 为DRFM干扰作用下差频信号频率随时间变化曲线,图中表示干扰信号延迟一个Tm1的干扰效果。可以看出由于发射波形采用了去周期化设计,相对于目标回波,DRFM干扰作用下的差频信号频率成分更加丰富,变化范围增大,不再具有明显的规律性。差频信号谐波能量分散,无法输出谐波幅度随距离变化的完整包络,干扰效果会受到抑制。
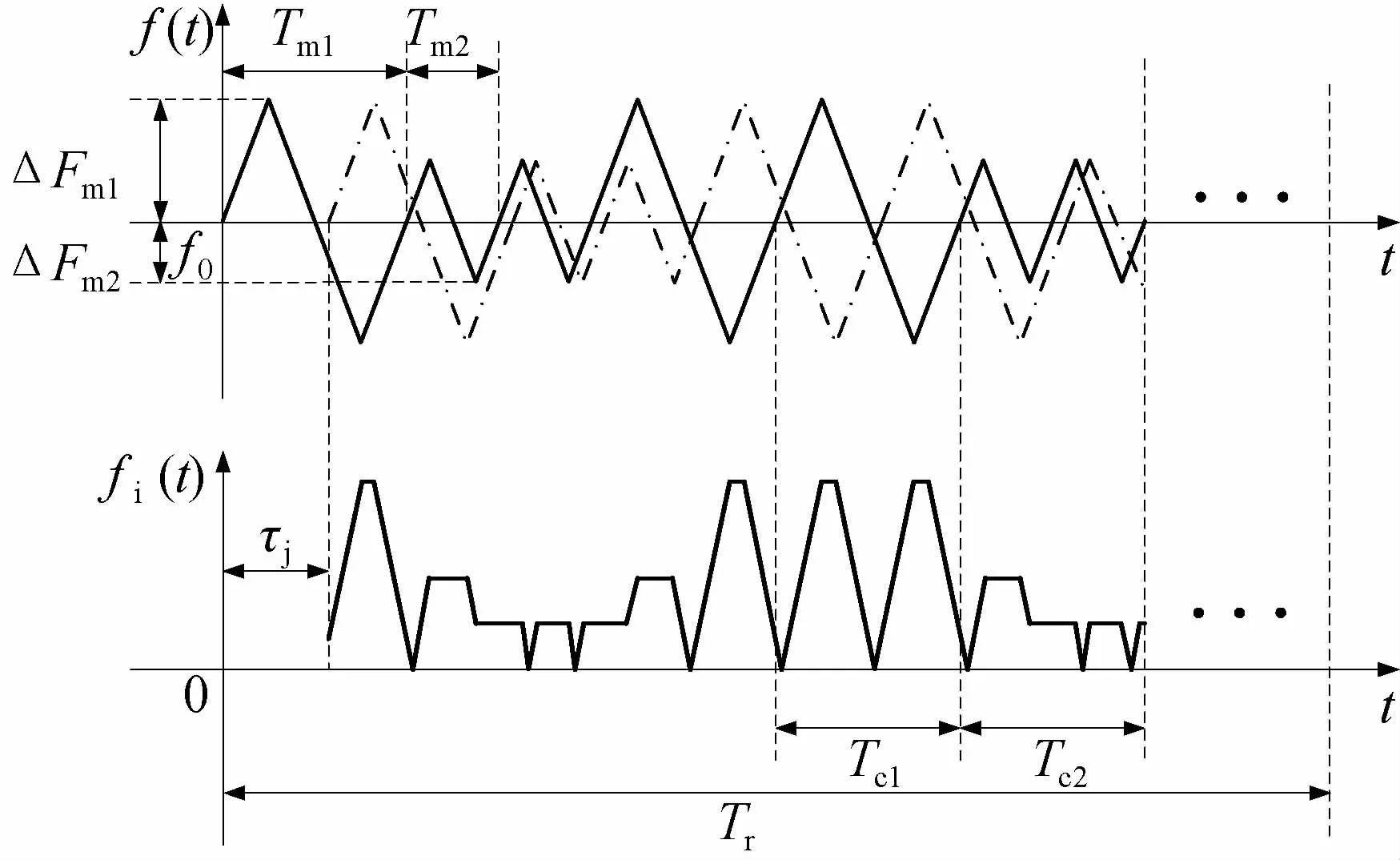
图7 DRFM干扰下差频信号时频图
2.3 双通道谐波时序检测方法
图8 为基于FFT的双通道谐波时序检测方法原理图,首先通过ADC以采样频率fs对差频信号进行N点采样。然后,通过N点的FFT运算获得差频信号离散频谱,提取频谱中各次谐波频率对应的谱线幅值作为各通道的谐波幅值。以N点为周期重复上述过程,即可得到各次谐波幅值序列,经检波后输出各次谐波幅度随距离变化的包络进行启动判决。
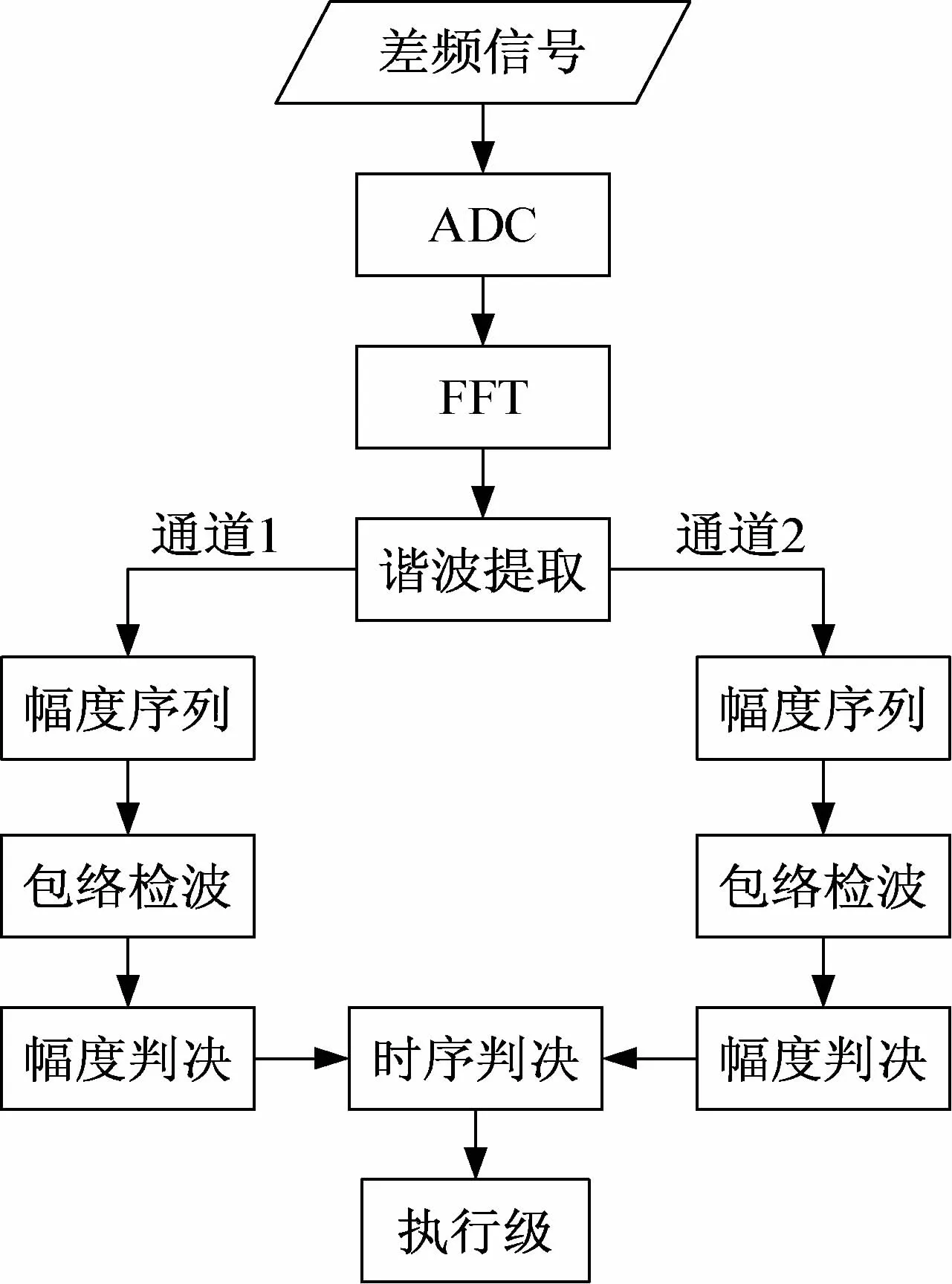
图8 双通道谐波时序检测方法原理框图
该方法中FFT点数的选取应考虑两方面因素。首先,在差频信号分析中,通过解析单一Tm内频谱得到各次谐波幅度随距离变化关系,进行FFT运算的采样时长应至少大于一个Tm。其次,考虑弹目交会过程中产生的多普勒效应作用于差频信号,相当于抑制载波的幅度调制,原有各次谐波谱线会被频率为mfm±fD两根谱线取代。为了减小多普勒效应的影响,设计FFT的频率分辨率fs/N 应远大于多普勒频率fD,从而利用FFT的泄漏使分散到mfm±fD的两根谱线上的能量集中到mfm谐波的谱线上。综上所述,FFT点数N的选取应满足条件:

3 仿真与实验结果
3.1 系统Modelsim仿真验证
为了验证本文设计的调频引信信号处理系统的定距与抗干扰性能,采用Simulink仿真模型生成的差频信号作为激励信号,通过Modelsim仿真环境观测系统各级输出信号。仿真参数:f0=3 GHz,fm1=100 k Hz,fm2=200 k Hz,ΔFm1=100 MHz,ΔFm2=50 MHz,伪随机序列长度P=4 095,码元宽度Tc=10μs。采样频率5 MHz,FFT点数64,选取400 k Hz和800 k Hz谐波通道,对应定距距离为3 m和6 m。弹目距离变化范围15 m~0 m,弹体飞行速度500 m/s,仿真时间30 ms,信噪比-10 d B。
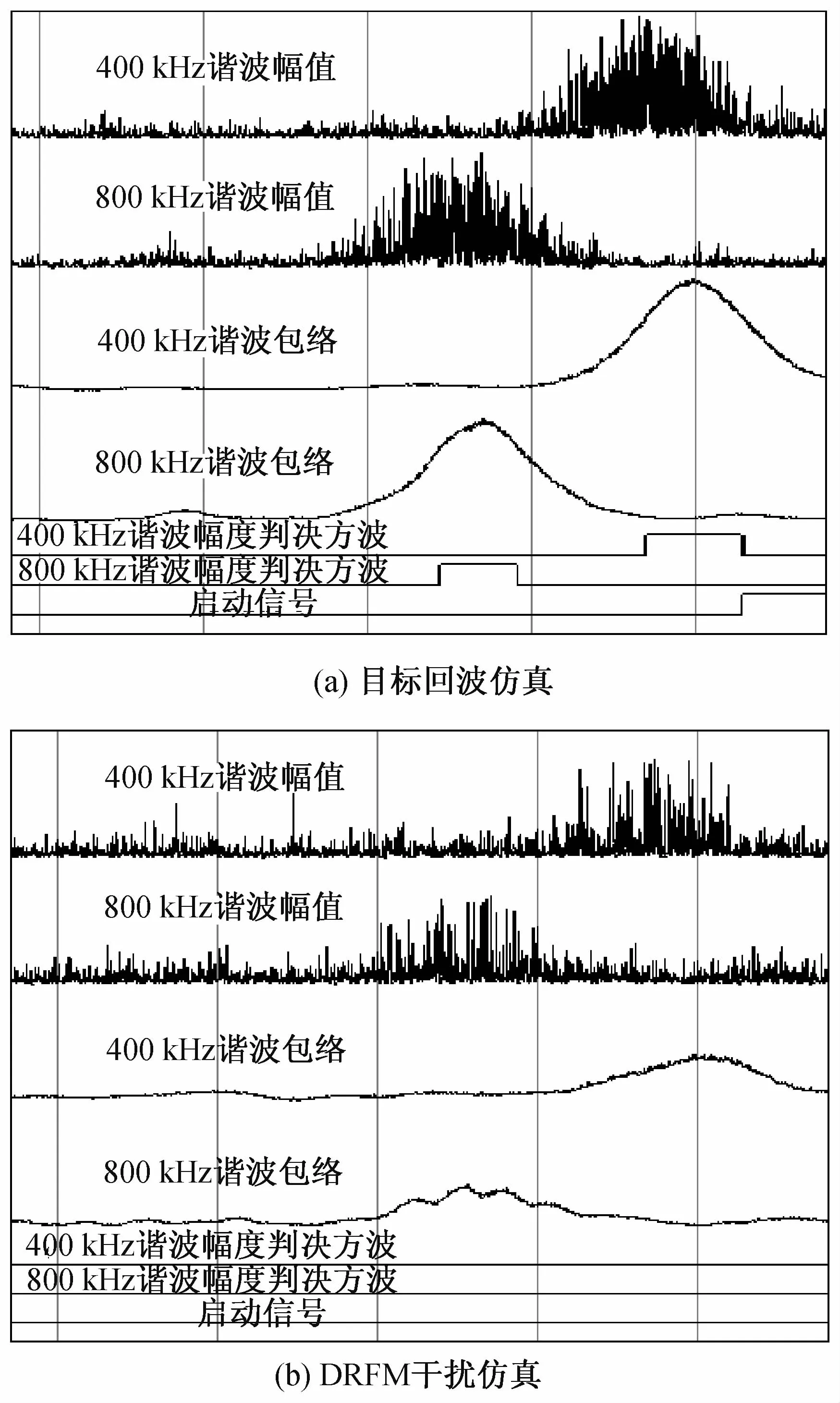
图9 调频引信系统Modelsim仿真结果
图9 (a)为目标回波作用下系统仿真结果,双通道谐波包络幅值大于幅度门限后输出方波信号,包络峰值对应距离分别为5.5 m和2.5 m。时序逻辑模块判断双通道输出方波信号的出现次序为高次谐波先于低次谐波,且间隔时间满足弹目接近速度变化范围,在弹目距离2 m附近输出启动信号。
图9(b)为DRFM干扰作用下的系统仿真结果,双通道谐波幅值明显小于目标回波,并且随时间分布规律相对杂散。双通道谐波包络信号峰值均小于幅度门限,无幅度判决方波信号输出,不满足启动判决条件从而无启动信号输出。
3.2 半实物仿真测试验证
利用现场可编程逻辑门阵列(FPGA)作为主芯片,设计制作引信信号处理电路,对该方案进行硬件验证。采用半实物仿真的方法,利用函数发生器分别产生目标回波与DRFM干扰作用下差频信号,作为信号处理电路的中频输入,通过示波器观测DAC输出的双通道包络检波信号。系统半实物仿真测试结果如图10所示。

图10 半实物仿真测试检波包络
可以看出,测试结果与仿真结果基本一致。目标回波作用下的双通道谐波包络完整,信号幅度峰值大于100 mV,且满足高次谐波峰值先于低次出现的时序关系,双通道谐波峰值时间间隔约为6 ms,对应的距离变化为3 m,经幅度与时序逻辑判决后可以输出启动信号。DRFM干扰作用下谐波包络与目标作用下差异明显,且信号幅度均小于50 mV,无法满足幅度判决条件。
设置DRFM干扰信号的初始延迟时间在0.975 Tm1~1.025 Tm1之间的敏感范围内,以10 ns为延时步进,进行50组抗干扰半实物仿真测试,双调制频率调频引信被干扰6次,抗干扰成功率为88%;传统调频引信被干扰27次,抗干扰成功率为46%。测试结果表明,双调制频率调频引信系统可以在满足定距性能的前提下,提高调频引信抗DRFM干扰的能力。
4 结论
本文在分析传统调频引信在DRFM干扰下失效机理的基础上,设计了以双调制频率随机跳变的三角波线性调频信号作为发射波形的调频引信抗DRFM干扰方法,提出了基于FFT的谐波时序检测方法判别目标,并通过Modelsim仿真分析与硬件测试验证了该抗干扰方法可以在满足系统定距性能的前提下,提高调频引信的抗DRFM干扰性能。

