目标速度对合成一维距离像的影响分析
段云鹏, 李国光
(北京遥感设备研究所,北京100854)
0 引言
雷达目标的像包括三维像、二维像和一维像,尽管目标的三维像和二维像包含目标的信息更多,但是实际中得到好的三维像和二维像却非常困难。雷达目标一维像虽然包含目标的结构信息比二维或三维像明显减少,但一维像的获取要简单得多[1]。因此,研究雷达目标一维像的获取方法具有实际意义。雷达目标一维像是由其对应的二维像分别在雷达发射方向(即纵向)及其垂直方向(即横向)上的投影,因而它又分为一维横向像和一维纵向像。通常来说,一维横向像是其对应二维像在其纵向方向所有回波的矢量和,它是通过运动补偿及多个周期回波(窄带信号)的多普勒处理来得到的。而一维纵向像是其对应二维像在其垂直方向所有回波的矢量和,它是通过发射窄脉冲或宽带信号而获得的[2-4]。一维横向像需要十分精确的运动补偿,往往很难做到,而一维纵向像只需要雷达发射(综合)窄脉冲,其回波即是目标的一维纵向像,处理简单且实时性强,特别地,当纵向分辨率足够高时,一维纵向像反映了目标精细的几何结构特征,而一维横向像主要是针对低分辨雷达提出来的[5-6]。
对于处在远距离的目标,雷达的波束宽度常常远大于目标形体对雷达的张角,这时要依靠雷达的角分辨率来区别目标的各组成部分是很困难的,如果使用逆合成孔径技术对运动目标进行距离-多普勒处理,则不但在横向上(方位)能分辨出目标的细节,而且在纵向上(距离)也能得到目标的结构特征。这种同时获得目标横向与纵向高分辨率的逆合成孔径雷达(ISAR)技术,近年来得到国内外雷达界的广泛关注与重视,目前利用ISAR实现雷达目标成像是一个重要的研究课题。
对于一个待成像的目标来说,目标相对雷达的运动可以分解为平动分量和转动分量,ISAR成像的机理就是要对其平动分量进行运动补偿,并利用转动分量-目标的旋转中心(散射中心),对目标进行转台成像[7]。纵向距离的高分辨率可以通过发射窄脉冲或宽带信号来获得,对于B·τ≈1的脉冲雷达来说,雷达的距离分辨率可以定义为ΔR≈c/2B,纵向高分辨率的获得一般不要求目标与雷达间有相对运动,只需要雷达发射(综合)窄脉冲,其回波即是目标的一维纵向像[8]。横向距离的高分辨是通过多普勒处理获得的,因而要求目标与雷达间具有相对运动。
1 静止目标的合成距离像
线性调频脉冲雷达在每个脉冲重复周期内发射一个Chir p脉冲。设脉冲重复周期为Tp,脉冲宽度为τ,且定义tm为以第m个周期的开始时间t=mTp为起点时间的变量,则第m个周期的发射信号可以表示为

式中:f0为发射信号的频率;φm为第m个周期的发射信号相位;A为发射信号的幅度;K为频率调制斜率。
发射信号的频率为

发射信号的频率变化范围为[f0,f0+B],B=Kτ称为调制带宽,λ=Bτ称为脉冲信号的时间带宽积;对于线性调频脉冲,λ≥1。
雷达发射信号可以表示为

对于调制带宽为B的线性调频脉冲压缩雷达,根据雷达系统理论,其距离分辨力为c/2B(c为光速)。对于窄带调频情况,如果c/2B≫L(即距离分辨单元宽度远大于目标尺寸L),可以将目标作为点目标看待。目标状态在相对静止的情况下,假设目标距离为R,R小于雷达的最大作用距离Rmax=c(Tp-τ)/2(即每个周期的、经过延迟的目标回波仍然落在本周期内,不会延迟到下一周期,每个周期的回波信号与本振信号具有相同的相位基准φm);同时假设R大于遮挡距离,即2R/c≥τ;则第m个周期的回波信号可以表示为

式中:U为回波信号的振幅,与发射信号的功率以及目标的雷达散射截面RCS有关。显然,sr(tm)为频率已知、幅度相位未知的信号。
根据统计检测理论,sr(tm)的最优检测为正交双通道相关积累检测。经过相参混频(抵消掉随机初始相位φm)、放大、零中频I、Q正交处理后的基带目标回波可以表示为

式中:S为信号的复振幅(包含放大器的幅相)。sb(tm)的实部表示I通道的零中频输出信号,虚部表示Q通道的零中频输出信号。由于存在接收机噪声,经I、Q处理后的信号可以表示为

式中:ε(tm)为复噪声,其功率与接收机的噪声系数、带宽、环境温度等有关。对于每个周期m,对信号sb(tm)进行双通道同步采样,采样间隔为Δt。Δt由调频带宽B(Δt≤1/B)和所要求的测距精度δR等因素决定。每个周期从tm=τ开始采样(对应的采样点编号n=0),至tm=Tp结束,实际采样点数为N=(Tp-τ)/Δt。
雷达接收机在每个周期的脉冲发射期间,即0≤tm≤τ时间范围内是不工作的,没有接收信号;对应的距离范围为0≤R<cτ/2,称为距离遮挡区;对于此距离范围内的目标,其回波脉冲信号的延时2R/c小于τ,2R/c至τ时间范围内的回波信号不会被接收,只有τ至2R/c+τ时间范围内的部分信号被接收,称为部分遮挡。
对于距离R≥cτ/2的非遮挡目标,回波信号sr(tm)经过采样后,占据的采样点数为 NT=τ/Δt,令nT=2R/(cΔt),则对于非遮挡目标,采样后的目标回波信号可以表示为
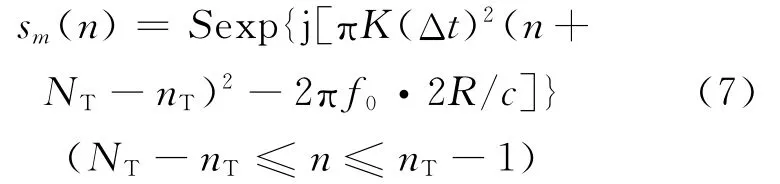
由于存在接收机噪声,实际的采样信号可以表示为

构造单位脉冲响应为如下形式的数字匹配滤波器

由于目标的距离R是未知的,或目标回波信号序列sm(n)的起始时刻nT-NT是未知的,常规的脉冲压缩处理方法将匹配滤波器hm(-n)进行周期为N的周期性延拓,在0≤k<N-1范围内对nT-NT进行搜索,根据目标函数最大处的k值对nT-NT进行估计。经过数字脉压后的输出序列为

根据信号与系统理论,式(10)中的卷积可以通过FFT实现

其中:
根据线性调频信号的匹配滤波原理,当nT≥NT,即目标处于遮挡区外时,|ym(k)|在kmT=nT-NT处取得最大值,根据kmT可以得到目标在第m个周期的的距离估计值为RmT=(NT+kmT)cΔt/2。
2 运动目标的合成距离像
考虑匀速运动目标情况,设目标相对径向速度为v。远离雷达运动时,速度为正;向雷达方向运动时,速度为负。第r个周期的回波信号可以表示为
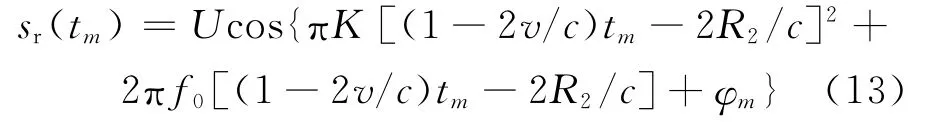
式中:R2=R+v mTp,R为第0个周期开始时刻的目标距离。
经过混频、放大与零中频I、Q正交处理后的基带目标回波可以表示为
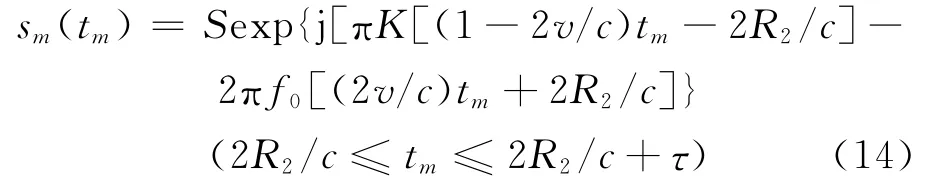
采样后的目标回波信号可以表示为
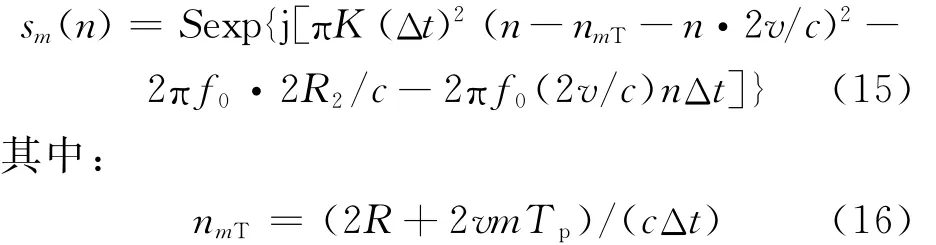
前向补零后,将信号起点从tm=τ延伸到tm=0,对应的采样点标号n=0。式(15)所示信号的相位可以表示为

式中:Φ0为与n无关的相位项。
显然,如果不进行运动补偿,则经过脉冲压缩处理后,第m个周期的压缩脉冲的峰值出现在

相对于第0个周期开始时刻,目标初始距离R的移动量为
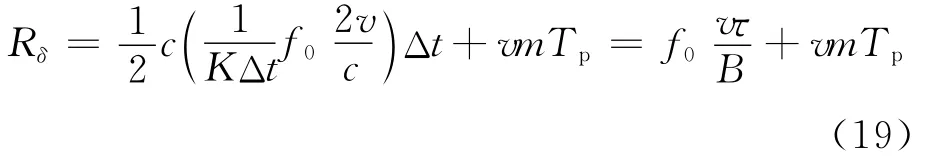
式中:f0vτ/B为距离测量的系统误差,又称为距离—多普勒耦合误差,需要通过τ、B的合理设计以及运动补偿来控制;vmTp为目标运动所引起的压缩脉冲的峰值位置在周期间的相对距离移动量,最大值为v MTp,M为积累检测所需的脉冲数。
考虑到[nmT,nmT+NT-1]与[nmT+2vf0/(KcΔt),nmT+2vf0/(KcΔt)+NT-1]这两个区间的重叠部分的点数为NT-2|v|f0/(KcΔt),则在不进行运动补偿的情况下,辛格脉冲的峰值由静止目标情况下的NT|S|下降到
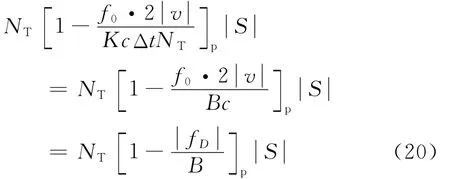
幅度损失的比例为|fD|/B,其中fD为运动目标的多普勒频率,即目标运动会导致脉冲压缩时的能量积累效率下降。
3 仿真结果及分析
参数设置:距离像起始点R0=900 m;目标的散射体个数为3;脉冲宽度τ=100μs;步进数n=64;步进频率Δf=10 MHz;脉冲重复频率fp=10 k Hz;散射体距离向量Sr=[908,910,912]m;散射体RCS向量SRCS=[100,10,1]m2;窗函数为汉明窗;距离分辨率ΔR=0.235 m;不模糊距离窗Ru=15 m。
计算机仿真结果如图1~图4所示。

图1 合成距离像(未补偿,v=100 m/s)

图2 合成距离像(补偿,v=100 m/s)
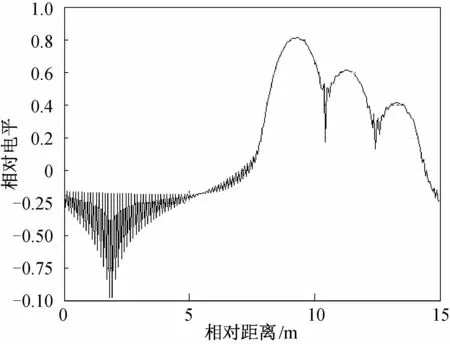
图3 合成距离像(未补偿,v=-100 m/s)
图1 为运动目标(v=100 m/s)的未进行速度补偿的合成距离像,图2为运动目标(v=100 m/s)的速度补偿后合成距离像。对比图1和图2,可发现三种状况:
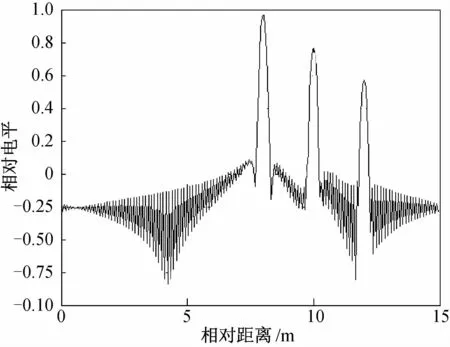
图4 合成距离像(补偿,v=-100 m/s)
a)合成距离像都能分辨出3个散射体,但图2的分辨能力更好;
b)未进行速度补偿的合成距离像存在明显失真,速度补偿后合成的距离像不存在失真现象;
c)图1中目标由预定的位置向左偏移了2×n×v/fp=1.28 m。
图3为运动目标(v=-100 m/s)的未进行速度补偿的合成距离像,图4为运动目标(v=-100 m/s)的速度补偿后合成距离像,对比图3和图4,也可发现三种状况:
a)合成距离像都能分辨出3个散射体,但图4的分辨能力更好;
b)未进行速度补偿的合成距离像存在明显失真,速度补偿后合成的距离像不存在失真现象;
c)图3中目标由预定的位置向右偏移了2×n×v/fp=1.28 m。
4 结论
本文以获得静止目标的合成距离像的方法为基础,分析了运动目标对回波脉冲压缩的影响。从时间膨胀率和多普勒频率偏移率的角度,分析了匀速运动目标情况下,合成距离像与静止目标合成距离像的差异,给出了运动目标合成距离像的补偿方法。对分析中使用的公式进行了详细推导,并对其参数作了说明,最后完成了仿真实验,验证了理论分析结果。

