一种弹载雷达频域抗拖曳干扰方法
蒋兵兵, 朱 剑, 汪 超, 李盘虎, 杨成杰
(上海无线电设备研究所,上海200090)
0 引言
脉冲多普勒(Pulse Doppler,PD)体制的弹载雷达具有测角精度高、副瓣电平低等优点。通过空-时自适应信号处理算法,能够提高其在杂波与干扰背景下的检测能力[1]。虽然弹载PD体制雷达具备上述优点,但对抗拖曳式诱饵干扰的能力有限。拖曳式诱饵干扰是一种自卫式电子对抗方式[2],诱饵通过拖曳线与被保护载机相连,载机平稳飞行时,两者具有一致的运动特性,弹载雷达跟踪系统难以通过运动特性区分目标和诱饵。现有实用的拖曳式诱饵多采用数字射频存储技术,通过联合距离拖曳、速度拖曳、RCS调制等复合手段[3],对雷达发射信号进行转发,使得诱饵与目标的回波信号具有高度的相似性,对弹载雷达的检测模块形成压制式或欺骗式干扰,使得诱饵和目标在波束内不可分辨,造成弹载雷达的速度、距离和角度跟踪环路无法正常工作。尤其当目标大机动时,会导致雷达系统波束指向锁定在拖曳式诱饵上,最终导致目标逃逸。
在跟踪初期的中远距离上,当目标与诱饵同时落入雷达阵面主瓣内时,两者的多普勒频率极为接近,PD体制雷达在频域上难以分辨出。通常情况下,拖曳式诱饵为达到欺骗干扰效果,其转发功率比需满足不小于2的条件[4]。故目标会淹没在诱饵的谱线中。当不采取抗干扰措施时,PD体制弹载雷达若单纯从频域检测目标,很大概率会错将诱饵当做目标,并进行后续判决跟踪及航迹起始[5]。虽然跟踪初期并不会有严重影响,但到了跟踪中期,正确检测目标的概率会大大降低。因此,有必要研究针对PD体制弹载雷达初始跟踪阶段的频域抗拖曳式干扰方法。
1 转发式拖曳干扰原理
在中远距离上,目标载机雷达发现威胁后,释放拖曳式诱饵,形成转发式拖曳干扰信号。由于弹目距离较远,且诱饵与目标具有同样的运动特性,因此不论此时弹目相对的态势如何,都无法在频谱上将目标回波与干扰信号区分开。干扰机容易捕获到制导雷达的速度跟踪波门。
转发式拖曳诱饵将收到的雷达探测信号放大后转发出去。载机飞行姿态的变化使得干扰信号和载机回波到达雷达天线的相位差随时间连续变化[6]。
拖曳式诱饵干扰弹载雷达工作的过程可分为以下三个阶段[4]:
a)在中远距离上,目标载机雷达发现威胁后释放拖曳式诱饵。此时,诱饵与目标运动特性一致,在雷达频谱上无法区分目标回波与干扰信号,干扰机很容易捕获制导雷达的跟踪波门;
b)干扰机捕获雷达跟踪波门后,目标通过机动,形成目标、诱饵、导弹之间的三角态势;
c)随着距离的逐渐接近,目标与雷达连线、诱饵与雷达连线之间的张角口逐步增大,导致目标、干扰的谱线逐步分离,但干扰信号功率更大,雷达会错选诱饵进行速度、角度跟踪。最终,目标逃到雷达波束以外,跟踪任务失败。
2 频域抗拖曳干扰方法
为保证PD体制弹雷达在转发式拖曳诱饵情景下的稳定跟踪性能,本文采用基于拟合的复调制ZFFT方法,使得PD体制的弹载雷达在初始跟踪阶段仍能检测出目标,从而实现频域抗拖曳式干扰,保证初始跟踪环路的正确建立。
(1)拖曳式诱饵与目标多普勒频差建模
目标释放拖曳式诱饵后,弹载雷达、目标及诱饵之间形成三角态势,如图1所示,其中vm为弹载雷达速度,vt为目标飞行速度,vj为拖曳式诱饵速度,θm为弹载雷达速度方向与弹目连线的夹角,θt为目标速度方向与弹目连线的夹角,θj为拖曳式诱饵速度方向与弹诱连线的夹角,Δθ为弹目连线与弹诱连线的夹角[7]。

图1 三角态势示意图
弹载雷达与目标相对运动产生的径向多普勒fmt为

弹载雷达与拖曳式诱饵之间的径向多普勒f mj为

考虑到诱饵与目标速度近似一致,即vj≈vt。由此可得,拖曳式诱饵与目标之间的径向多普勒频差为

(2)传统复调制ZFFT方法
复调制Zoom-FFT法(ZFFT)是目前广泛应用的一种频率估计方法,可在所选定的分析频率范围内对典型窄带信号的频谱结构进行细化。相同采样点数的条件下,ZFFT得到的频谱更细致。反之,相同频率分辨率条件,ZFFT方法比FFT方法需要更少的采样点数。故当出现多个频点集中在某个频带内,且难以获取精准的频率分辨率时,复调制ZFFT法可以对准这一区域的频带范围后,将该频带频谱中心移至零频,通过低采样率重新采样,再利用傅里叶变换进行分析,从而获取较细致的频谱[8]。
(3)提出的方法
在PD雷达的速度通道中,经抗混滤波,A/D采样及抽取后,速度检测通道的输入信号为离散序列为x[n],其中n=0,1,2,…,N-1,N 为速度检测通道信号的采样点数,采样率为fs。
首先,对x[n]作N 点FFT后,按照频谱峰值,选择检测频段为[f1,f2],并以此配置ZFFT的频谱细化范围。频谱细化倍数可表示为
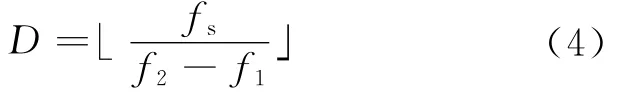
式中:·」表示向下取整。
按照复调制ZFFT方法,对频带中心的频移量为

故将fb移动到零频后的离散序列为

设计通带带宽为f2-f1的带有Hamming窗的FIR低通滤波器H(z),对此序列xb[n]进行低通滤波处理后得到序列xf[n],以采样率fs1=fs/D进行重采样,滤波抽取后的序列为

式中:n=0,1,…,N/D」-1。
对xc[n]进行N点FFT操作,则其频谱分辨率为
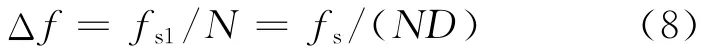
可以看出,此时的频率分辨率提高了D倍。
在存在拖曳式干扰时,第一峰值点即为拖曳式诱饵。故通过峰值检测,取第二峰值点对应的频率作为目标检测频点。虽然复调制ZFFT方法提高的频率分辨率,但是频率估计依然存在误差,需要对目标检测频点进行修正。
在xc[n]的频谱 Xc(k)中,k为谱线序号,第二峰值点的序号为l0,取其左右两侧的相邻谱线序号l0-1与l0+1。考虑到频谱峰值处的形状,本文采用二次曲线拟合方法进行修正[9]。
点[l0-1,Xc(l0-1)],[l0,Xc(l0)]与[l0+1,Xc(l0+1)]可以构成一条二次曲线。按照二次曲线的性质,则频率修正值为此二次曲线的对称线位置,即

其中

则最终本抗拖曳式干扰方法输出的目标频点为

所提方法的处理流程图如图2所示。
(4)本文方法与FFT的计算复杂度对比
FFT方法需要对ND点FFT进行处理,以获得fs/(ND)的频率分辨率,需要进行的复数乘法与复数加法次数分别为(ND/2)log2(ND),(ND)log2(ND);而采用本文方法获取相同的分辨率时,需要进行两次N点FFT处理与一次N点频移操作,则需要N log2N+N次复数乘法与2N log2N次复数加法。

图2 本文方法处理流程图
可以看出,本文方法尽管步骤较多,但在运算量上具有优势,同时频率分辨率更高,可以提升PD体制弹载雷达在跟踪初期从干扰信号中检测到目标的能力。
3 典型仿真场景结果
对于PD体制弹载雷达,雷达工作频率为7 GHz,如图1中所示,vm=800 m/s,vt=200 m/s。在初期的三角态势飞行过程中,θm的变化范围为8°~10°,θt的变化范围为10°~16°,Δθ=0.2°。
故拖曳式干扰与目标之间的多普勒频差如图3所示,此时的多普勒频差范围为8.9 Hz~14.7 Hz。

图3 拖曳式干扰与目标的多普勒频差
速度检测通道输入信号的时域信噪比为-15 d B,数据率为2 k Hz,采样点数为256。此信号经本振混频后的频率为Δfa=150.2 Hz。拖曳式诱饵的转发功率比为4,即干扰幅度为信号幅度的4倍。
对诱目多普勒频差为8 Hz~15 Hz的场景,通过10 000次Monte Carlo实验,分别采用本文方法与FFT方法进行检测。本文所提方法选用的频带范围为目标及干扰所在频带向左右两侧各拓展一半的增加的频带宽度。仿真实验结果给出了目标检测概率,目标检测相对误差及干扰检测相对误差,分别如图4,图5及图6所示。

图4 目标检测概率对比图
在图4的多普勒频差较小场景中,本文目标检测概率更高更稳定,FFT方法对多普勒频差较小的目标检测无能为力。图5中的目标检测相对误差也证实了本文所提方法的目标检测性能。FFT方法对目标检测结果已经严重错误,但本文方法能够将相对误差控制在10%以内,在多普勒频差更小的情况下,将相对误差控制的2%以下。图6中的干扰检测结果中,FFT方法的效果更好,但可以看出,适度增大本文方法中选用的频带范围,可以减小干扰检测相对误差。

图5 目标检测相对误差对比图

图6 干扰检测相对误差对比图
以上的仿真结果表明:本文方法可在较高准确度下,在频域分辨出目标与拖曳式干扰,实现频域抗拖曳式干扰。联合可靠的速度跟踪环路后,可以保证PD体制弹载雷达在探测目标初期阶段航迹起始的准确度,防止后期被拖曳式诱饵带偏,提升目标跟踪有效性。
4 结论
在传统复调制ZFFT方法的基础上,联合二次曲线拟合,提出了弹载雷达频域抗拖曳式干扰方法。通过理论分析与计算机仿真,本文方法相比于FFT方法在频率分辨率,计算复杂度及目标检测性能上更具优势。

