例析高中化学计算题的解题技巧

花俊

[摘要]化学计算题种类繁多，计算过程复杂，若只按照常规方法解题，不但浪费时间而且正确率无法保障。因此，掌握一些特殊的解题技巧，对提高化学计算题解题效率非常重要。常见的解题技巧有推断估算法、极限假设法、十字交叉法等。

[关键词]化学计算；解题技巧；推断估算法；极限假设法；十字交叉法

[中图分类号]G633.8 [文献标识码]A [文章编号]1674-6058（2017）23-0069-01

高中化学计算题贯穿整个化学学习过程，是教学的重难点。虽然计算题的题型种类繁多，但是学生若能掌握一些特殊的解题技巧，则可大大提高解题效率。

一、推断估算法

推断算估法是解决复杂化学计算题的一种特殊的、简便的方法。此方法主要適用于选择题的解答。有些选择题看似需要经过复杂计算才可以得到答案，但经过仔细分析、细细琢磨便可发现，通过简单估算推断即可得到准确答案。

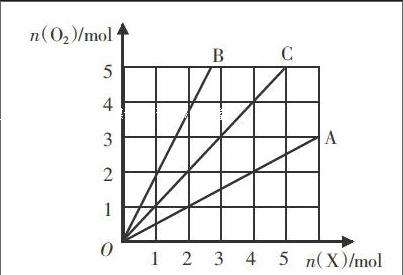
[例1]如右图所示，可燃性气体X（X=A、B、C）完全燃烧时所消耗的物质的量n（X）用横坐标表示，消耗的氧气的物质的量n（02）用纵坐标表示，A、B是两种可燃性气体，C是A、B气体的混合物，则C中n（A）：n（B）为（ ）。

A.2：1 B.1：2 C.1：1 D.任意

分析：本题是推断估算法运用中的一道典型例题。通过结合题目给定的信息进行推断估算，则可达到快速解题的目的，而且大大提高了解题的正确率。

解：据图可知，1molA消耗0.5molO₂，1molB消耗2molO₂；若A、B以1：1混合时，则1mol C消耗1.25molO₂，然而图中1mol C消耗1molO₂，因此可以推断出A、B混合物，n（A）：n（B）>1：1，结合给定答案可知，A为正确选项。

评注：推断估算法是一种特殊的解题方法，学生在平时的学习中，需要对这类题目多加练习，做好归纳总结，为快速高效地解题打好基础。

二、极限假设法

在解决化学计算问题的过程中，由于某些问题给定的条件模棱两可或者条件缺失，导致不能直接计算出准确的结果，这时可以假设处于某种极限条件下，再根据假设求得计算值的范围。极限假设法是一种特殊的解题方法，需要根据具体情况具体分析。

[例2]在某未知浓度的硝酸中溶解22。4 g的单质铁，反应后总共收集到0.3 mol NO₂和0.2mol NO。则下列选项中正确的是（ ）。

A.反应后生成的盐只有Fe（NO₃）₃

B.反应后生成的盐只有Fe（NO₃）₂

C.产物中Fe（NO₃）₂和Fe（NO₃）₃的物质的量之比为1：3

D.产物中Fe（NO₃）₂和Fe（NO₃）₃的物质的量之比为3：1

分析：经分析可知本题产物不能确定，可能为Fe（NO₃）₂或者Fe（N₃）₃，还有可能是二者的混合物。根据本题的特点可以用极限假设法进行求解。

解：用极限假设法分析，当产物只有Fe（N₃）₃时，转移的电子数为1.2mol；当产物只有Fe（N₃）₂时，转移的电子数为0.8mol。而实际的转移电子数为：0.3×1+0.2×2=0.9（mol）。因此产物为Fe（N₃）₂和Fe（N₃）₃的混合物。设Fe（N₃）₂和Fe（N₃）₃的物质的量分别为a、b，则a+b=0。4，2a+3b=0.9，联立两式解得：a=0.3，b=0.1，答案为D。

评注：这是一道典型的可运用极限假设法解答的题目。用极限假设法解题不但可以缩短解题时间，而且可以提高解题的正确率。

三、十字交叉法

十字交叉法主要应用于二元混合物或组成的计算过程中，由二元一次方程公式演变而成。如果题目给定两个组分的总量和二者的平均值，求二者之间的比例，即可用此方法计算。十字交叉法是一种特殊的计算方法，熟练应用后可达到高效解题的目的。

[例3]现有100 g的Li₂CO₃和BaCO₃的混合物，当它们和一定浓度的HCl溶液反应时，所消耗的盐酸量和100 g CaCO₃消耗的该浓度的盐酸的量相等。计算该混合物中Li₂CO₃和BaCO₃的物质的量之比（ ）。

分析：题目中，碳酸锂与碳酸钡的分子量是隐藏的已知条件，给定的Li₂CO₃和BaCO₃的混合物的质量可以看作二者的平均分子量。

解：根据十字交叉法：

因此，Li₂CO₃和BaCO₃的物质量之比为97：26。

评注：本题是采用十字交叉法解答的典型例题，通过解题过程可知，此种方法的解题过程简单明了，可以帮助学生少走弯路。

综上所述，解决化学计算题的方法有很多，但是掌握特殊方法，在某种程度上可以大大提高解题的效率和正确率。学生在学习过程中需做好归纳总结，根据各题目的特点，选择最高效的解题方法。

（责任编辑罗艳）endprint