基于多层图布局算法的不确定性网络可视化方法

陈炳坤，周 虹



基于多层图布局算法的不确定性网络可视化方法

陈炳坤，周 虹

(深圳大学计算机与软件学院，广东 深圳 518060)

由于越来越多的数据包含了不确定性，可视化不确定性网络最近几年成为了数据可视化领域中的一个热点。在现有的不确定性可视化研究中，基于概率图布局的方法取得了比较好的效果，通过一种固定采样图算法，可以很好地可视化不确定性网络，并反映出网络中的概率分布情况。针对基于概率图布局的方法存在运行时间过长、图布局不稳定等问题，提出了一种基于多层图布局的方法，改进了多层图布局算法并与固定采样图算法相结合，弥补基于概率图布局的不确定性网络可视化方法的缺陷。实验证明改进之后的算法与原来的方法相比具有更高的时间效率，而且生成的图结构更加稳定。

不确定性可视化；多层图布局；概率图；图固定算法

图(graph)在数据可视化中占有重要的地位，图也叫网络，一般由结点和边组成。通过图可以帮助人们更好地理解数据，了解数据的内部结构。有不少针对确定性网络的可视化方法已经被提出，但是目前有很多应用包含的数据都带有不确定性，为了更好地理解这些数据，不确定性可视化方法便应运而生。FENG等[1]使用了一种基于密度的方法来可视化统计中的不确定性，主要是通过核密度估计的方式估计多个样本的密度函数，使用密度函数进行可视化，但是其方法只适用于平行坐标。TAK和TOET[2]使用了颜色来表示不确定性，随着不确定性变化，颜色会发生改变。MACEACHREN等[3]采用了一种实证研究，研究了在不确定性可视化中，不同视觉变量和符号对可视化的直观性造成的影响，并得出结论认为不确定性可视化应该关注模糊性。近年来，把图可视化与不确定性可视化结合也得到了广泛的关注。GUO等[4]研究在图的边上表示不确定性，把4种不同的视觉变量及其组合用于边的不确定性描述上，对比其效果。VEHLOW等[5]研究了重叠社交结构网络的不确定性可视化方法，因为在社交网络中，一个对象可以同时存在于多个社交团体中，可以在可视化的过程中引入不确定性的概念。

SCHULZ等[6]提出了一种基于概率图布局(probabilistic graph layout)的算法，通过数据产生图的概率模型，使用概率模型采样得到不同的图，最后把这些图结合成最终的可视化效果。本文把基于概率图布局的方法简称为Schulz方法，使用Schulz方法能够可视化不确定性网络及其统计属性，能够很好地反映出不同实例之间的概率分布。Schulz方法主要分为两部分，一部分为图的布局算法，另一部分为图的渲染算法，其中生成图布局的过程中存在着时间过久、布局不稳定等问题，针对这些问题，本文提出一种基于多层图布局的方法加以改进，使Schulz方法具有更好的性能。

1 基于概率图布局的不确定性网络可视化方法

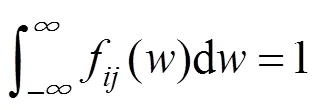
一般情况下，可以使用简单的离散函数来进行问题的讨论，即

其中，为边存在的概率，对应的边权重为1；1–为边不存在的概率，对应的权重为0，表示节点和节点无穷远。节点之间的距离可以使用权重的倒数(1/)表示，在使用力引导算法计算图的布局时可以用1.5倍的最远距离来表示无穷远。文献[6]方法基本流程如图1所示，总的来说包含4个步骤。

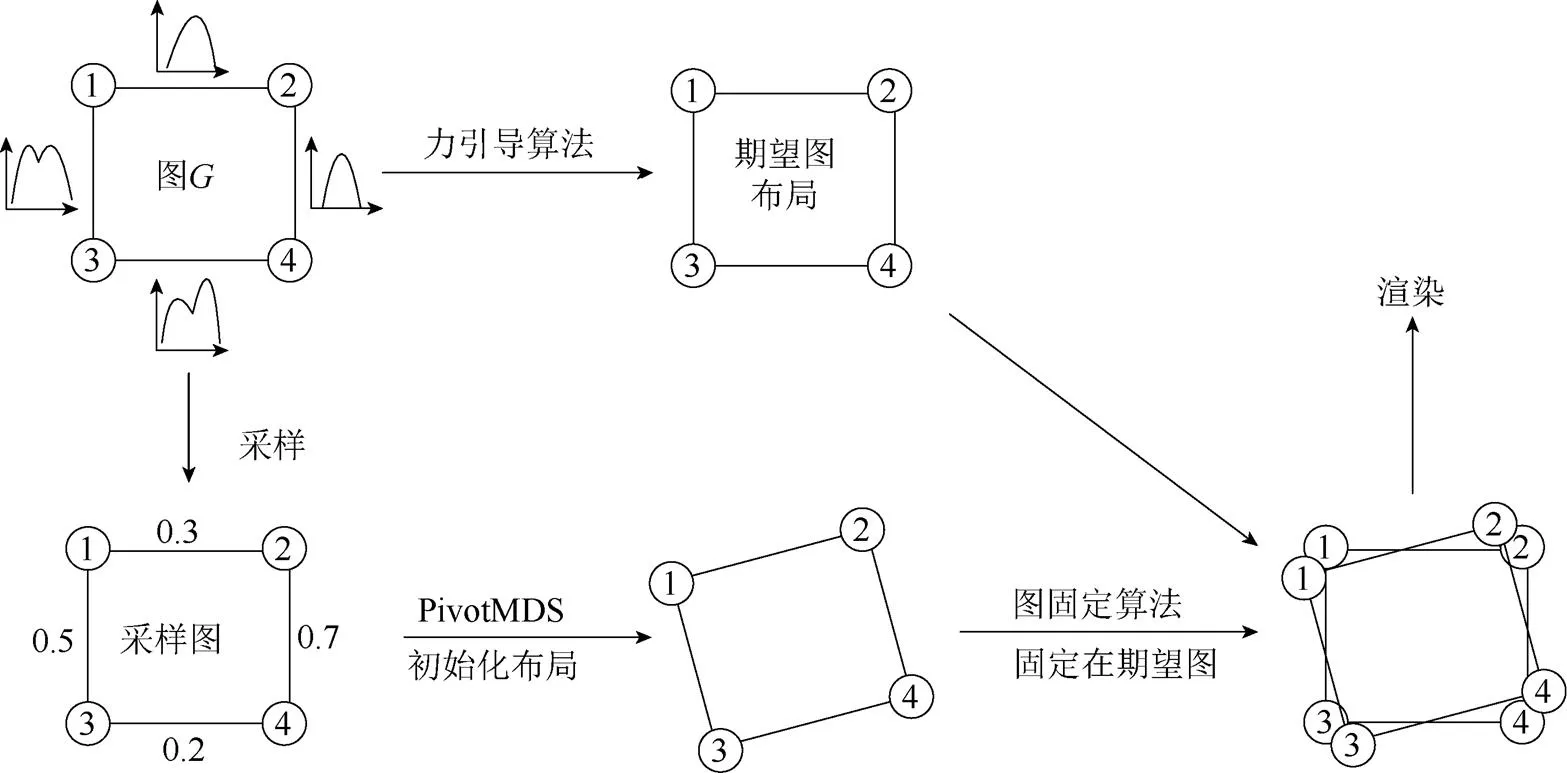
图1 Schulz方法的流程示意图

1.1 生成期望图布局

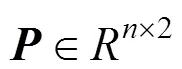
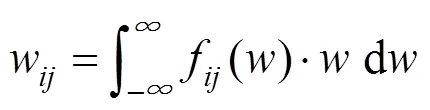
1.2 采样得到采样图

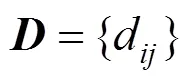
1.3 图固定算法

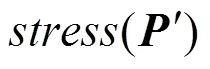
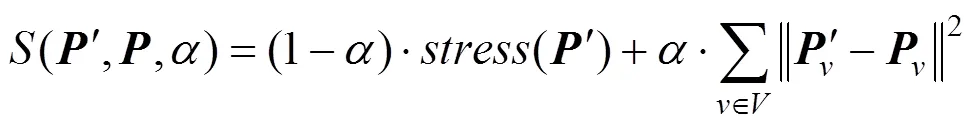
1.4 渲染

通过多次采样并固定采样图后，可以对固定在一起的多个图进行渲染，Schulz方法中为了可以反映出概率图的概率分布，主要采用了node splatting算法[10]和edge splatting算法[11]进行渲染。图2(a)为Schulz方法可视化的效果图，而图2(b)为对应期望图布局。

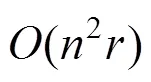
图2 Schulz方法可视化不确定性网络例子

2 基于多层图布局算法的不确定性网络可视化方法

本文采用多层图布局算法对Schulz方法中的固定算法进行改进，提出了基于多层图布局算法的不确定性网络可视化方法，简称为MLSchulz方法。图3为MLSchulz方法的主要流程图。在计算期望图布局的过程中使用了多层图布局算法，在固定采样图的过程中也使用了多层图布局算法，但是因为要进行固定采样图的操作，需要对多层图布局算法进行一些改进。另外多层图布局算法首先生成较小的图，再一步步扩充，因此无需使用PoivtMDS等算法进行图布局的初始化。

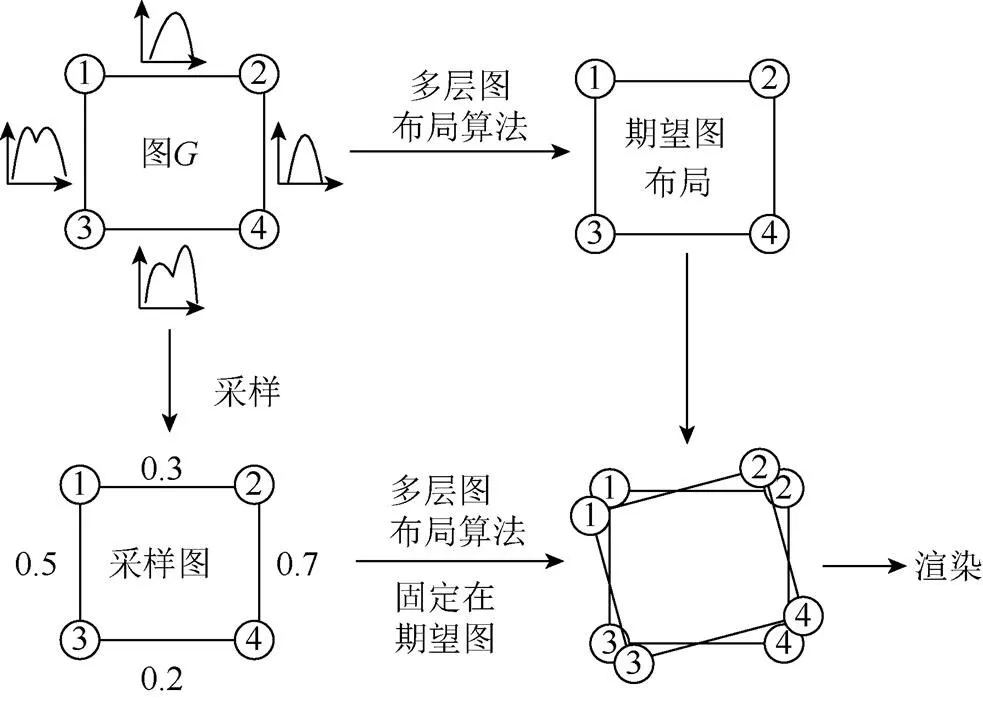
图3 MLSchulz方法的流程示意图

2.1 多层图布局算法

力引导算法具有容易实现且绘图效果好等优势得到了广泛的使用，但是当图的规模到了一定的程度时，力引导算法的运行时间会很长。因此有很多研究人员提出了多层图布局的算法。多层图布局算法求解图的布局不是一步到位的，而是一个从粗糙到精细的过程。

多层图布局算法一开始只对粗糙图(只包含少数节点的图)进行力引导算法，然后逐步扩展粗糙图得到最终结果，因此速度上有较大提升。HAREL和KOREN[12]提出了一种高效的多层图布局算法，MLSchulz方法在该算法的基础上进行改进。文 献[12]的多层图布局算法的流程如下：

设置初始值为初始粗糙图的节点数，一般初始化为10以内的数。为两层粗糙图间节点增长的倍数，=3。为概率图(,)的节点总数。

步骤1. 计算概率图节点间的最短距离矩阵，随机初始化图的布局，令=，为当前粗糙图包含的节点数。

步骤2. 在图中找出个中心节点的集合，在最短距离矩阵中取出个中心点之间的距离矩阵，在布局中找出该个中心节点的布局。

步骤3. 使用力引导算法重新计算这个中心节点的位置，=(,)。

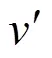
步骤5. 增加的值，=×，若值小于等于，则转到步骤2，否则结束。

其中，距离矩阵为×矩阵，使用图布局算法计算图的二维布局，因此布局为×2矩阵，每一行表示一个点的二维坐标。步骤2中的矩阵为×矩阵，即个中心点之间的距离，为×2矩阵。此外步骤2中求出个中心节点的过程可以使用一种近似的中心算法[13]得到，具有更高的效率且最终得到的图布局效果区别不大。

2.2 多层图布局算法生成期望图布局

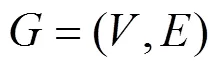
步骤1. 计算图中个节点间的最短距离矩阵，随机初始化图个节点的布局。

步骤3. 在最短距离矩阵中取出个中心点之间的距离矩阵，在布局中找出该个中心节点的布局。

步骤4. 根据式(4)使用力引导算法重新计算个中心节点的位置，=(,)。

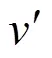
步骤6. 增加的值，=×，若值小于等于，则转到步骤2，否则结束并保存好队列，在计算采样图的过程中还要使用。

2.3 多层图布局算法固定采样图布局

在使用多层图布局算法计算并固定采样图布局时，与先前的多层图布局算法不同。因为在计算期望图布局时已经把每一层粗糙图所用到的中心点保存下来了，因此在计算并固定采样图布局时，无需使用k-center算法，也无需初始化和等参数。直接从队列中抽取出每一层所要用到的中心点，从采样图中抽取相应的节点，再优化能量函数即可。在计算采样图每一层粗糙图布局的过程中使用的能量函数为式(6)。采样图计算和固定的过程如下：

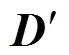
步骤2. 遍历队列，取出下一个粗糙图包含的所有节点集合放入，因此中包含该层粗糙图的所有中心点。

步骤3. 在距离矩阵′中找出集合中所有点的距离矩阵，记为′，从布局′中找出中所有点的布局，记为′作为中心点，同样也要在期望图布局中找出包含所有点的布局。

步骤4. 根据式(6)，使用力引导算法重新计算集合里中心节点的位置′，′=(′,′,′)。

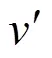
步骤6. 若遍历完队列，则结束，否则返回步骤2。

3 实验结果和分析

使用Schulz方法和MLSchulz方法分别进行3组实验，对比分析两种方法的性能。第1组实验使用随机生成的概率图进行时间对比，第2组实验使用合成数据集和真实数据集对比两种方法的可视化效果，第3组实验为验证两种方法的布局稳定性。

3.1 时间对比

MLSchulz方法和Schulz方法主要的时间都集中在固定采样图上，即优化式(6)的过程。为了更好地对比MLSchulz方法和Schulz方法在时间上的差异，MLSchulz方法和Schulz方法一样采用了GANSNER等[14]提出对式(6)的优化方法，对比两种算法的时间效率。另外还要对比两种算法收敛后得到的能量函数值，能量函数值为式(6)的值，从而得知两种方法优化结果的差异。

在实验中，首先随机生成10~200个点的概率图，再使用两种方法对这近200个概率图进行可视化，每个概率图进行10次采样。得到两种方法对于每个概率图所得到的最终能量函数值和运行时间，如图4所示。可以看出，MLSchulz方法在时间上要远远优于Schulz方法，大约可以节省一半的时间。此外，在图4(b)中运行的时间曲线在局部有下降的趋势，出现这种现象的主要原因有：①在图布局开始时会随机初始化点的位置，不同的随机值会对运行时间产生少量影响；②实验中所使用的概率图是随机生成的，带有一定的随机性，但是运行时间在总体上会随着节点变多而增大。图4(a)为两种方法最终得到的能量函数值，相差不大，说明使用了多层图布局算法进行固定可以减少时间且不会导致优化效果的下降。

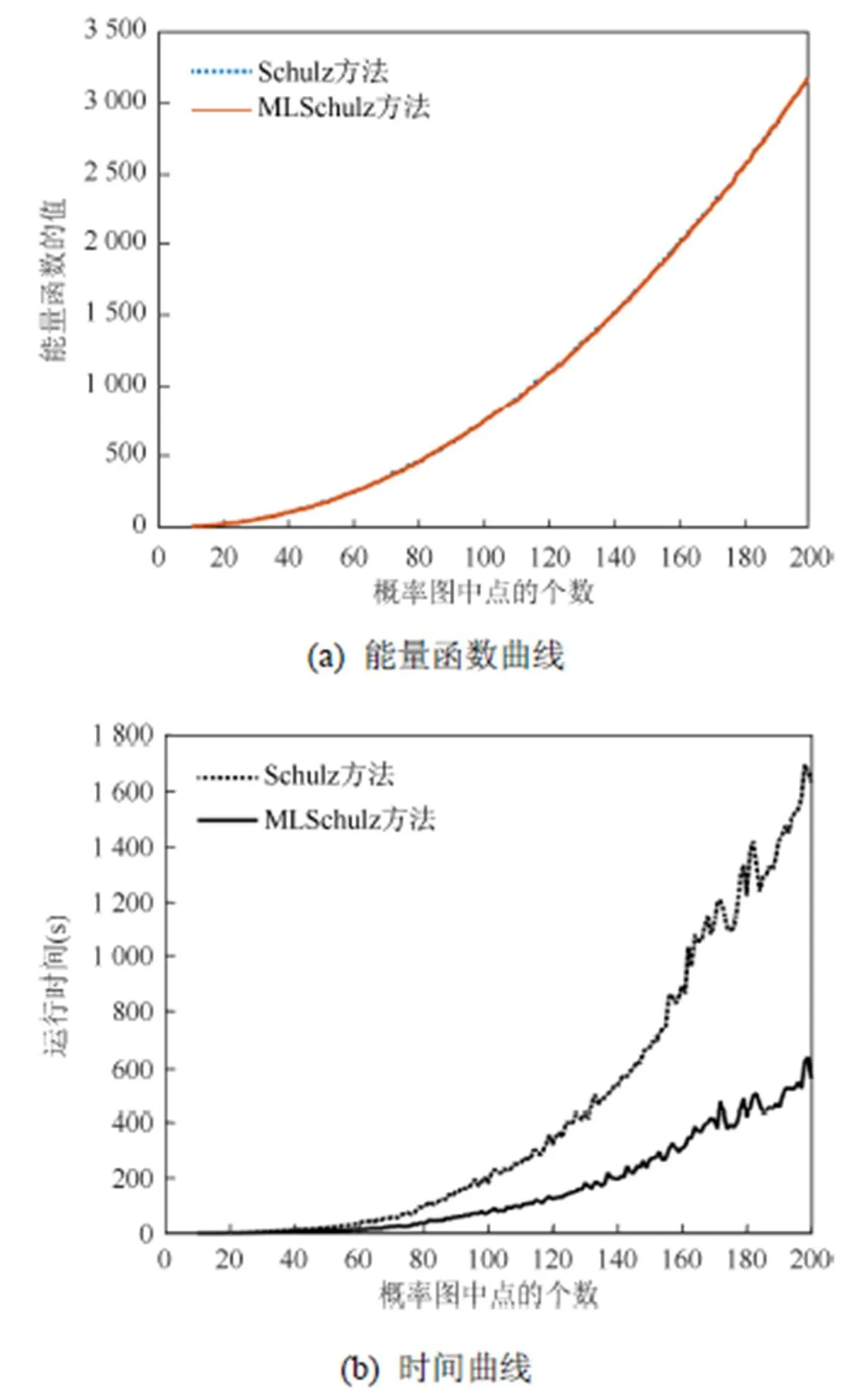
图4 两种方法性能的对比

3.2 布局对比

实验中使用了4种数据对比两种方法的可视化效果。其中两种数据为合成数据，另两种为从String数据库[15]中下载的蛋白质数据。

3.2.1 合成数据

首先使用合成数据来验证MLSchulz方法和Schulz方法的效果，图5(a)为一个合成的矩阵图，矩阵图包含5个节点和8条边。其中，每一条边的权重分别符合一个离散概率分布，图5(b)为该矩阵图的边所符合的离散概率分布。

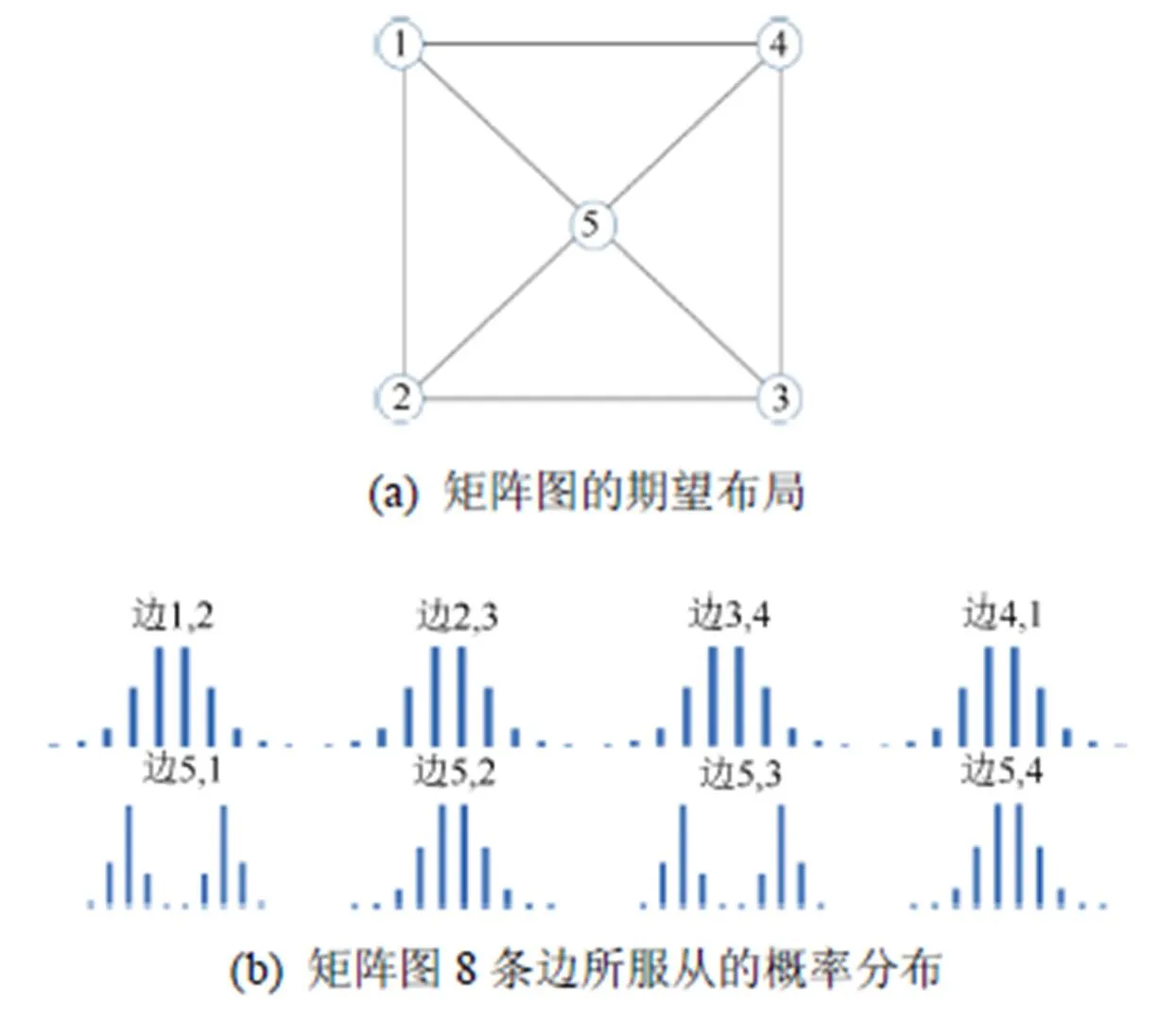
图5 合成矩阵图的期望布局及边的概率分布

从图5(b)可以看到，除了边5,1和边5,3，其余的边权重的分布都是单峰的，是一个类似高斯分布的离散分布。而边5,1和边5,3所服从的分布包含两个峰。对此矩阵图进行可视化，验证可视化结果能否反映出该图的概率分布，并对比两种方法的效果。图6为两种方法的可视化效果，采用的值均为0.3，采样1 000次。

从图6(a)和图6(b)可以看到，节点5明显分为了3个节点簇，分别往节点1和节点3的方向偏移。观察节点1和节点3也可以发现，节点1和节点3也分为了3个簇，而节点2和节点4则只有一簇。说明了两种方法都可以比较好地反映出边5,1和边5,3的双峰分布，存在两个出现频率较高的权重。可以发现两种方法在小的数据集上具有相似的可视化效果，并且都可以在一定程度上反映出数据集的概率分布。

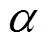
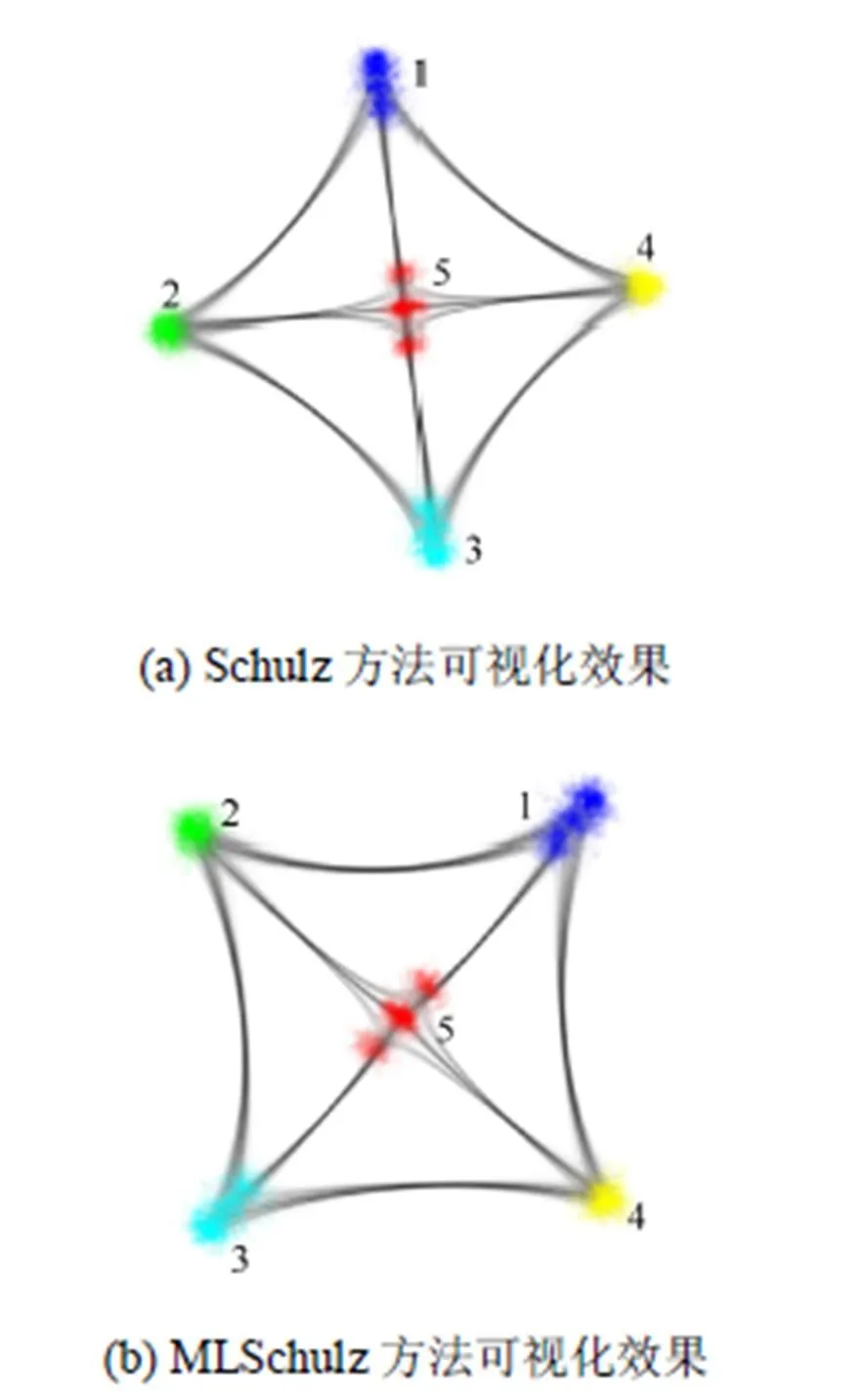
图6 两种方法在合成矩阵图的可视化效果

图7 两种方法在合成三叉树数据中的可视化效果

3.2.2 蛋白质数据

从String数据库中下载真实的蛋白质数据测试MLSchulz方法的效果，蛋白质数据集中包含了蛋白质之间发生联系的概率，即联系系数。实验中采用了两组蛋白质数据集：Amy2数据集和Amy数据集。Amy2数据集包含了11种蛋白质，而Amy数据集包含了31种蛋白质数据。

首先使用Amy2数据集进行实验，表1为Amy2数据集的联系系数表，可以看出Amy2蛋白质与数据集中其余的蛋白质之间都具有联系系数。在实验中使用离散形式的概率函数，如式(2)所示，权重只有1和0。例如Si和Amy2的联系系数为0.934，则在采样的过程中Si和Amy2之间权重为1的概率为0.934，而权重为0的概率为0.066。因此在生成期望图时，两种蛋白质之间的期望权重等于联系系数，而两种蛋白质之间的距离为联系系数的倒数，在计算完最短路径后要使用1.5倍的最远距离代替无穷远。

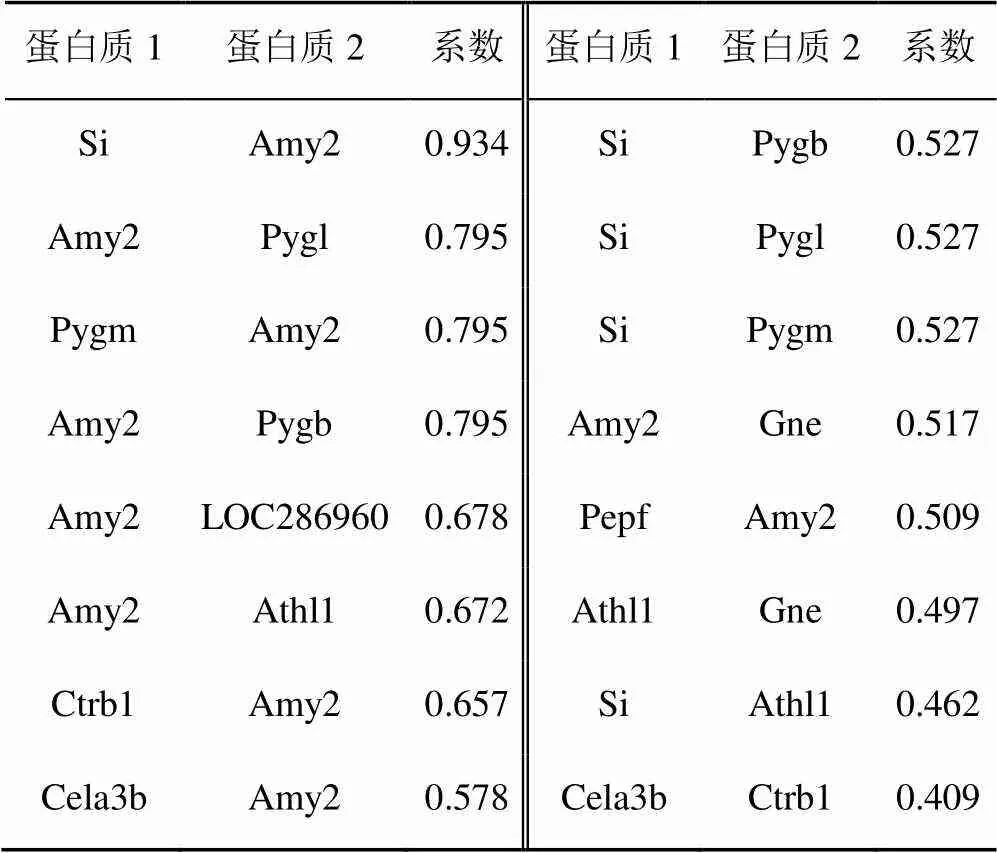
表1 Amy2蛋白质数据集

两种方法可视化的结果有较大差别，可以通过表1中各蛋白质的联系系数，对比两种方法的可视化效果能否正确反映蛋白质间的关系。因为每种蛋白质与Amy2之间都存在联系的可能，根据这些蛋白质与Amy2联系系数由大到小排列，可以把蛋白质分为4组。第1组为(Si)，第2组为(Pygl，Pygm，Pygb)，第3组为(LOC286960、Athl1、Ctrb1)，第4组为(Cela3b、Gne、Pepf)。第1组蛋白质与Amy2之间的联系系数最大，因此在可视化的结果中应该离Amy2蛋白质最近。而第4组蛋白质与Amy2蛋白质之间的联系系数最小，因此在可视化的结果中应该离Amy2蛋白质最远。从图8可以看出，两种方法的可视化结果都大致符合这一规律，说明两种方法均可以较好地反映出蛋白质之间的联系。

图8 两种方法在Amy2数据集中的可视化效果

图9 两种方法在Amy数据集中的可视化效果

3.3 布局稳定性

图10 MLSchulz方法的流程示意图

4 结束语

本文主要基于文献[6]中的不确定性网络可视化方法(Schulz方法)，从时间效率和布局稳定性两方面对其进行了改进，提出了一种基于多层图布局算法的不确定性网络可视化方法，即MLSchulz方法。MLSchulz方法可以有效的改进Schulz方法的运行速度，适应更大的概率图。另外多层图布局算法实现的过程是逐步由粗糙到精细的，在优化的过程中不容易陷入局部最小，因此也提高了布局的稳定性。但是本文算法仍有很多地方值得研究和改进，目前使用的优化方法速度较慢，需要研究一种更好的优化方法，从而提高优化能量函数的速度且不影响优化效果；MLSchulz方法在初始化每一个粗糙图的时候只使用了上一个粗糙图的布局信息，可以对其改进同时利用上一个粗糙图和期望图的布局信息进行初始化。

[1] FENG D, KWOCK L, LEE Y, et al. Matching visual saliency to confidence in plots of uncertain data [J]. IEEE Transactions on Visualization & Computer Graphics, 2010, 16(6): 980-989.

[2] TAK S, TOET A. Color and uncertainty: it is not always black and white [EP/OL]. [2018-01-05]. https:// repository.tudelft.nl/view/tno/uuid:3e36b35d-eadf-47de-a25c-9a639402da26.

[3] MACEACHREN A, ROTH R E, O´BRIEN J, et al. Visual semiotics & uncertainty visualization: an empirical study [J]. IEEE Transactions on Visualization & Computer Graphics, 2012, 18(12): 2496-2505.

[4] GUO H, HUANG J, LAIDLAW D H. Representing uncertainty in graph edges: an evaluation of paired visual variables [J]. IEEE Transactions on Visualization and Computer Graphics, 2015, 21(10): 1173-1186.

[5] VEHLOW C, REINHARDT T, WEISKOPF D. Visualizing fuzzy overlapping communities in networks [J]. IEEE Transactions on Visualization & Computer Graphics, 2013, 19(12): 2486-2495.

[6] SCHULZ C, NOCAJ A, GOERTLER J, et al. Probabilistic graph layout for uncertain network visualization [J]. IEEE Transactions on Visualization & Computer Graphics, 2017, 23(1): 531-540.

[7] KAMADA T, KAWAI S. An algorithm for drawing general undirected graphs [J]. Information Processing Letters, 1989, 31(1): 7-15.

[8] BRANDES U, PICH C. Eigensolver methods for progressive multidimensional scaling of large data [C]// International Symposium on Graph Drawing. Berlin: Springer-Verlag, 2006: 42-53.

[9] BRANDES U, MADER M. A quantitative comparison of stress-minimization approaches for offline dynamic graph drawing [C]//International Symposium on Graph Drawing. Berlin: Springer-Verlag, 2011: 99-110.

[10] VAN LIERE R, DE LEEUW W, et al. GraphSplatting: visualizing graphs as continuous fields [J]. IEEE Transactions on Visualization & Computer Graphics, 2003, 9(2): 206-212.

[11] HOLTEN D. Hierarchical edge bundles: visualization of adjacency relations in hierarchical data [J]. IEEE Transactions on Visualization & Computer Graphics, 2006, 12(5): 741-748.

[12] HAREL D, KOREN Y. A fast multi-scale method for drawing large graphs [J]. Journal of Graph Algorithms & Applications, 2002, 1984(3): 183-196.

[13] HOCHBAUM D S. Approximation algorithms for NP-hard problems [M]. New York: Word Publishing Company, 1997: 37-39.

[14] GANSNER E R, KOREN Y, NORTH S. Graph drawing by stress majorization [C]//GD’04 Proceedings of the 12th International Conference on Graph Drawing. Berlin: Springer, 2004: 239-250.

[15] SZKLAREZYK D, FRANCESECHINI A, KUHN M, et al. The STRING database in 2011: functional interaction networks of proteins, globally integrated and scored [J]. Nucleic Acids Research, 2011, (39): 561-568.

Uncertainty Network Visualization Method Based on Multilevel Graph Layout Algorithm

CHEN Bingkun, ZHOU Hong

(College of Computer Science & Software Engineering, Shenzhen University, Shenzhen Guangdong 518060, China)

Visualizing uncertainty networks has become a hot topic in the field of data visualization in recent years, because more and more data contains uncertainties. In the uncertainty visualization research, a method based on the probability graph layout is fairly effective by using an anchoring algorithm to make good visualization of uncertain networks and reflect the probability distribution of the networks. However, the method has two limitations, the high time complexity and unstable layout. To address these issues, we propose an uncertainty network visualization method based on multilevel graph layout algorithm. This method combines the multilevel graph layout algorithm with anchoring algorithm, and improves the limitations of the original method. Experimental results demonstrate that our improved algorithm has higher time efficiency compared with the original method, and the generated graph structure is more stable.

uncertainty visualization; multilevel graph layout; probabilistic graph; graph anchoring algorithm

TP 391

10.11996/JG.j.2095-302X.2018061130

A

2095-302X(2018)06-1130-09

2018-03-08；

2018-06-04

国家自然科学基金青年科学基金项目(61103055)

陈炳坤(1993-)，男，广东湛江人，硕士研究生。主要研究方向为信息可视化。E-mail：chenbingkun03@163.com

周 虹(1982-)，女，湖南长沙人，讲师，博士。主要研究方向为信息可视化和可视分析。E-mail：hzhou@szu.edu.cn