末敏弹扫描角变化规律研究*
郑 斌,于 涛,雷永信
(西安现代控制技术研究所,西安 710065)
0 引言
末敏弹稳态扫描状态即为弹以一定落速v、扫描角θ(弹轴与铅垂轴夹角)和转速ω(弹轴与铅垂轴形成的平面绕铅垂轴转动速度)运动的状态[1],如图1所示。这时,弹落速和绕铅垂轴的转速变化均很小,扫描角因弹可以绕柱铰轴转动而发生变化(通常伞弹连接等价为柱铰方式)。

图1 稳态扫描状态
由于弹上敏感轴和威力轴均相对于弹轴设置,当扫描角存在时,末敏弹在地面形成由外向内收缩的阿基米德扫描螺线轨迹,在此轨迹上一旦探测识别并定位目标即起爆战斗部形成EFP弹丸攻击目标顶部。扫描角变化不仅会影响扫描轨迹,还直接影响探测、识别和定位性能,进而影响系统命中率[2]。扫描角变化规律研究目前多采用多刚体动力学或刚柔结合动力学模型研究[3-5],并通过立式风洞吹风和外场飞行试验进行符合校准。文中根据末敏弹稳态扫描阶段运动特性,建立末敏弹在绕铅垂轴旋转主伞带动下围绕悬挂点运动的绕心方程,得出扫描角变化解析模型,进而分析影响参数和影响规律,研究结果可为末敏弹扫描角参数设计提供依据。
1 模型和影响参数
稳态扫描状态下末敏弹运动,可以假定为在绕铅垂轴匀速旋转主伞带动下的末敏弹绕定点运动[6]且落速恒定,不考虑主伞和悬挂点的摆动。为便于分析,建立弹体坐标系C-XYZ,如图2所示,C为质心,C-YZ平面为弹轴与铅垂轴形成的平面(即弹子午面),C-XY平面为过弹质心的横截面。A为弹悬挂点,h为A点到C点的位置矢量,弹在悬挂点受力方向铅垂向上,rc为弹质心矢径。C-X0Y0Z0为圆心在C点的伞体坐标系,CZ0轴铅垂向上且坐标系绕该轴匀速旋转,转速ω即为伞转速。如图3所示,C-X0Y0Z0坐标系分别绕三轴进行3次旋转θ、φ、γ即得到C-XYZ坐标系[3]。
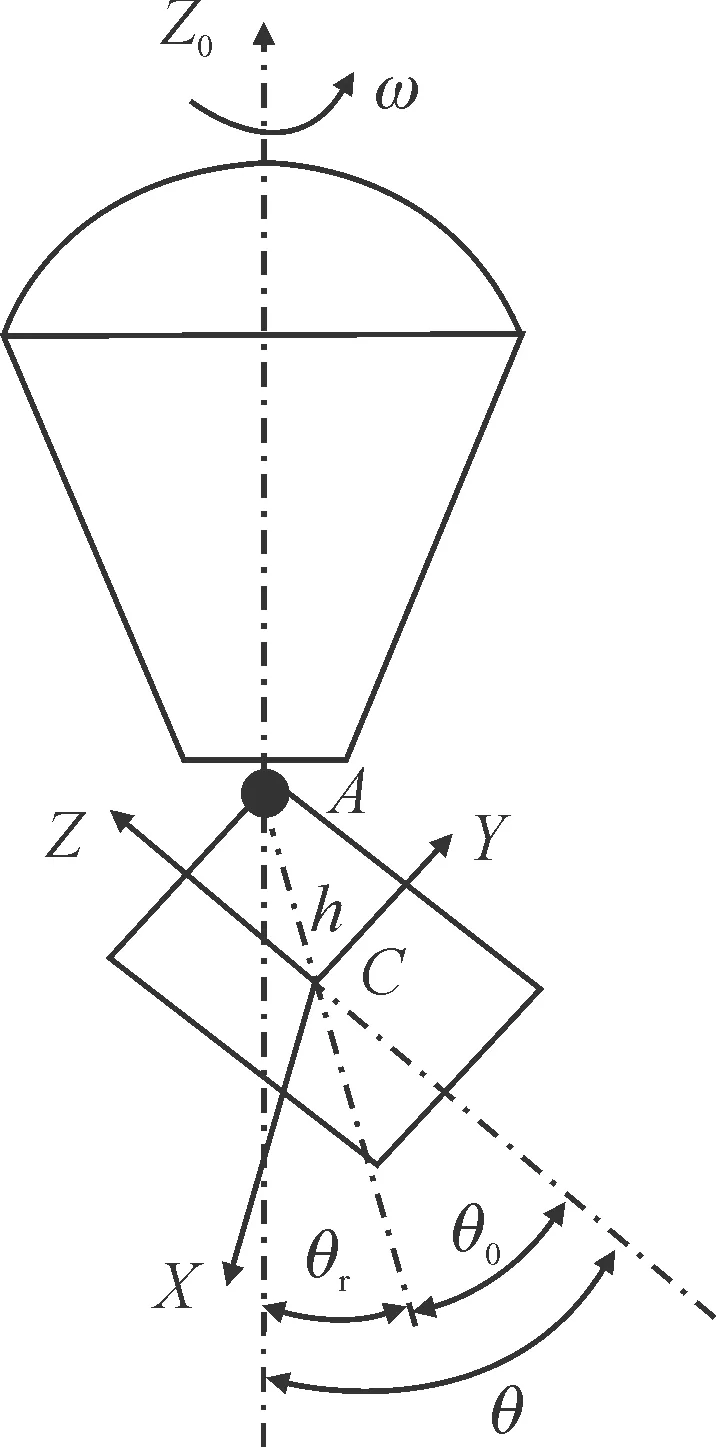
图2 弹体坐标系
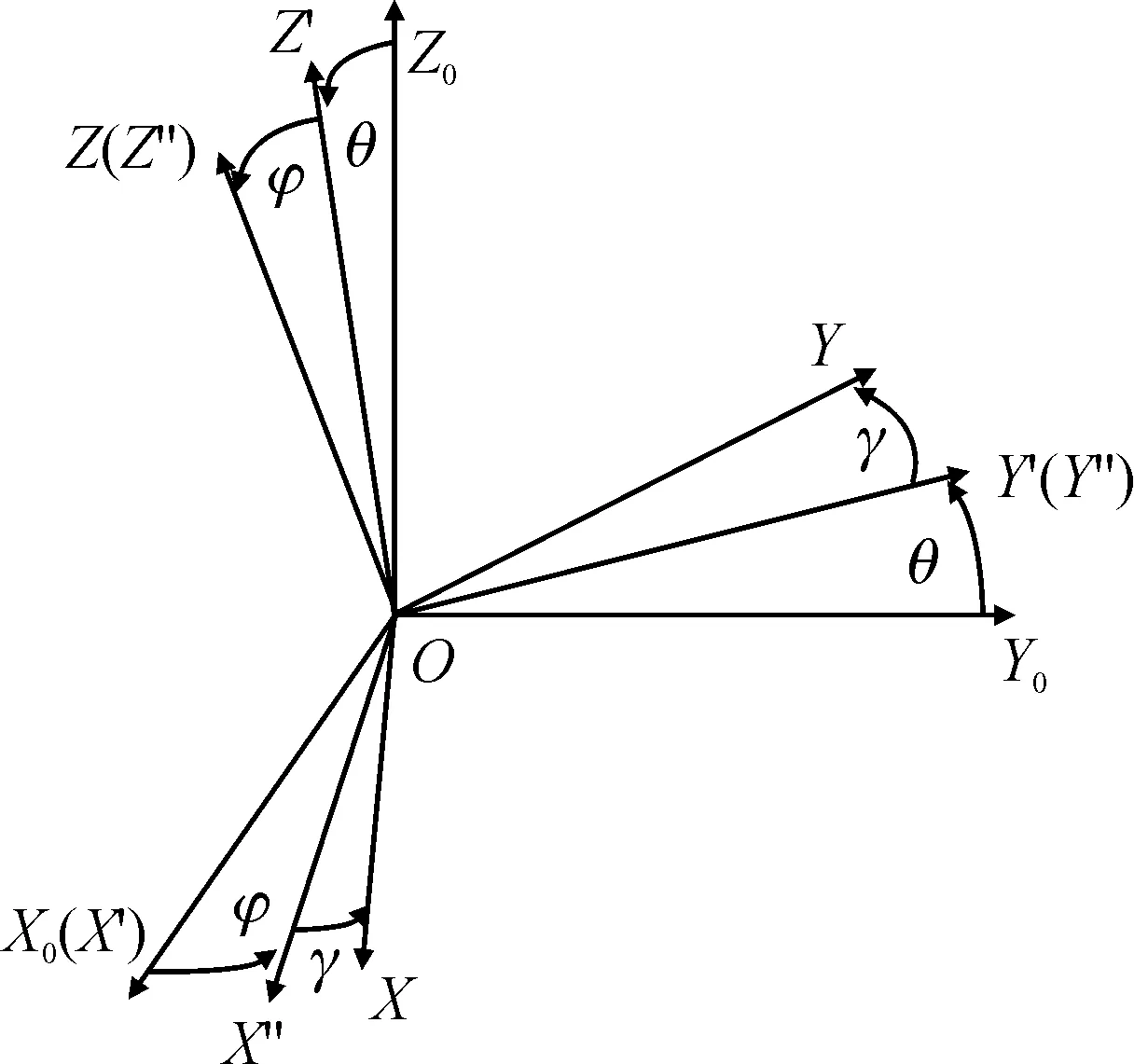
图3 伞体坐标系
通常末敏弹为轴对称体,3个坐标轴即为过质心惯性主轴,令三轴转动惯量分别为Jx、Jy、Jz、m为弹质量,ωc为弹角速度(弹体系分量为ωx、ωy、ωz),My和Mz为弹体对悬挂点的反力矩,因此绕心方程为[4-5]:
(1)
通常伞弹悬挂点为柱铰连接方式,末敏弹子午面本身摆动很小,因此可以假定扫描角变化主要在子午面内,进一步导出扫描角变化解析式。
令θ为扫描角,θ0为静悬挂角,θr为扫描角在子午面内变化量,则有:θ=θ0+θr。

(2)
实际上,扫描角θ围绕一均值变化,令此均值为θ*,扫描角θ围绕均值θ*在子午面内变化量为δr,则有:θ=θ*+δr,通常说的稳态扫描角即为扫描角变化均值θ*,扫描角变化频率即为δr围绕扫描角均值θ*在子午面内摆动频率。
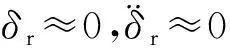
由式(2)得扫描角变化均值为:
(3)
进一步可近似为:
(4)
扫描角均值变化量近似为:
(5)
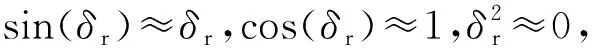
(Jz-Jy)ω2cos(2θ*)]δr=0
(6)
由式(6)得扫描角在子午面内变化频率为:
(7)
综上式(3)~式(7)可见,扫描角变化均值与弹质量m,转动惯量Jy、Jz,转速ω和悬挂参数h相关,扫描角变化频率还与转动惯量Jx相关。同时,由式(1)可见,扫描角变化还与弹初始扰动参数θ0、φ0、γ0相关[7]。
2 主要参数影响规律
仿真分析影响扫描角变化的主要参数,仿真中采用的一组基本参数为:m=5.5 kg,Jx=0.015 6 kg·m2,Jy=0.0135 kg·m2,Jz=0.010 9 kg·m2,h=0.098 m,ω=3.5 r/s。
1)转动惯量Jx、Jy、Jz和静悬挂角θ0影响
当Jx=Jy时,从式(4)和式(5)可见:第一,当Jy=Jz,扫描角变化均值即为静悬挂角;第二,当Jy>Jz,扫描角变化均值大于静悬挂角,反之,小于静悬挂角;第三,转动惯量比Jy/Jz越大,扫描角变化均值和变化幅值均增大。
当Jx≠Jy时,随Jx与Jy差值增大,扫描角变化均值和幅值均增大,但若转动惯量比接近1(即Jy/Jz及Jx/Jz接近1),则增大程度不显著;反之,则扫描角变化均值会显著增大(相比Jx=Jy情况),如当Jy=Jx=0.021 kg·m2时,扫描角变化均值为6.9°,但若Jy与Jx不相等(Jy=0.0195 kg·m2,Jx=0.0215 kg·m2)时,扫描角变化均值为20°(如图4所示)。

图4 扫描角摆动平均值随Jx、Jy的变化规律
Jx还影响扫描角变化频率,由式(7)可见:当Jx大于Jz时,扫描角变化频率会减小,但通常弹的Jx=Jy,因此也会增大扫描角变化幅值。
2)初始扰动影响
图5为θ0、φ0分别取1°、5°和10°时弹轴角度变化,可以看出:初始扰动值增大,扫描角变化的均值和变化幅值均增大,初始值为1°、5°、10°时,扫描角摆动的平均值分别为1.2°、6°、11°,摆动幅值为±0.2°、±1.5°、±3.2°。因此,初始条件设计时应尽可能保证弹开伞时处于较稳定状态。

图5 角度变化
3)转速ω影响
由式(4)和式(5)可见,转速ω增大,扫描角变化均值和幅值均增大,且转速变化量Δω增大,扫描角变化幅值也会增大,如图6所示。
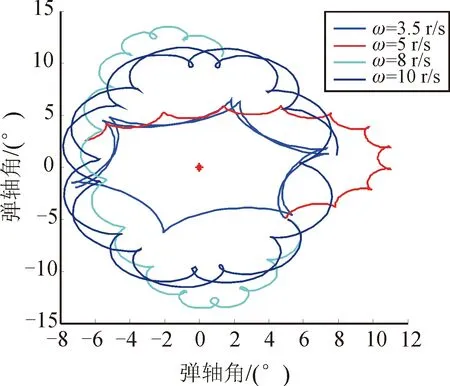
图6 弹轴在单位圆上投影图
分析式(3)可见,扫描角变化的本质是由于转速产生的惯性离心力矩和质心偏离静悬挂位置产生的悬挂力矩的平衡,若弹静态悬挂轴即为惯性主轴,则式(3)可变为:
(8)
若扫描角偏离角度δr时,悬挂力矩要使其回到平衡位置,需满足:
(9)
由于δr是小量,故:
(10)
由式(10)可见,在h、m、Jy和Jz设计参数一定的情况下,弹转速若大于ωmax,扫描角变化会不稳定,即变化均值和幅值显著增大;并且,ωmax的值随质量m增大、或悬挂参数h增大、或Jy及Jz差值变小而增加。在本节的基本参数条件下ωmax为7.1 r/s左右,图6所示,当弹转速大于7.1 r/s时,扫描角变化均值及幅值均显著增大。因此,工程上增大弹质量,有利于提高弹的转速适应范围,即增大弹质量,在转速一定时扫描角更稳定。
另外,转速对扫描角的影响同样与Jx和Jy的差值相关,当差值增大时,会放大转速对扫描角的影响,如图7(a)与7(b)对比所示。

图7 转速对扫描角的影响
4)质量m和悬挂点参数h影响
质量和悬挂参数均会影响扫描角大小,由式(4)、式(5)和式(10)可见,m和h越大,则扫描角变化均值和幅值均减小,同时扫描角稳定的允许转速范围也越大。因此,工程上在满足约束条件情况下,增大弹质量m和悬挂参数h,有利于扫描角稳定。
3 结论
扫描角变化与静悬挂角、悬挂参数、质量、转动惯量、转速等主要设计参数以及初始扰动相关,仿真分析表明:转动惯量比越接近1、质量和悬挂参数越大、静悬挂轴与惯性主轴越重合、转速不超过最大范围均有利于扫描角稳定。

