中口径预制破片弹反导能力研究*

陈红彬,师军飞,高 波,王 勇

(1 南京理工大学机械工程学院,南京 210094;2 陆军研究院炮兵防空兵研究所,北京 100080;3 辽宁庆阳特种化工有限公司,辽宁辽阳 111002)

0 引言

中大口径高炮由于射速低、反应慢及配备的火控、引信落后,二战对空命中率低,战后防空任务逐渐被小口径高炮与近程防空导弹代替[1]。近年来,电磁干扰制约了导弹的防空效能,而空袭平台的远程精确化需要近程防空体系具备较高较远的防空能力。中口径火炮防空反导能力研究重新成为热点[2-3]。

为满足战争对导弹、无人机等多种小型目标的防御需求,AHEAD弹通过改进弹药的设计思想,携带质量相对较大、数量相对较少的前向飞散破片,在目标前方较佳位置形成高动能、高密度的破片弹幕,达到对目标的有效命中和毁伤[4]。文献[5]建立了AHEAD弹反导射击效率模型,文献[6]研究了AHEAD弹不同散布误差下开舱距离对毁伤效能的影响规律。中口径炮弹若装填AHEAD弹型预制破片,相同弹幕破片密度下弹幕覆盖范围更广,显然中口径火炮防空更依赖于炸点的精确控制及开舱条件的优化,因此有必要研究其对中口径火炮反导能力的影响。

文中提出预制破片在中口径炮弹舱室内的排布方式,分析开舱后破片运动规律,建立中口径预制破片弹对空中典型目标反辐射导弹的射击效率模型。在已知误差统计特性的基础上,结合某近炸引信启动准则,采用仿真模拟法来评估中口径火炮反导能力。

1 破片舱室内排布结构及运动规律

中口径预制破片式防空炮弹结构类似于AHEAD弹,杀伤元素是舱室内预先排布的多圈圆柱形钨合金破片,但在弹底增加一定抛射药,赋予开舱后破片更高的附加轴向速度。单层排布直径dp、质量mp的破片ND枚,沿母弹轴向排布np层,破片总数NpD=npND,单层破片的装填方式如图1所示。

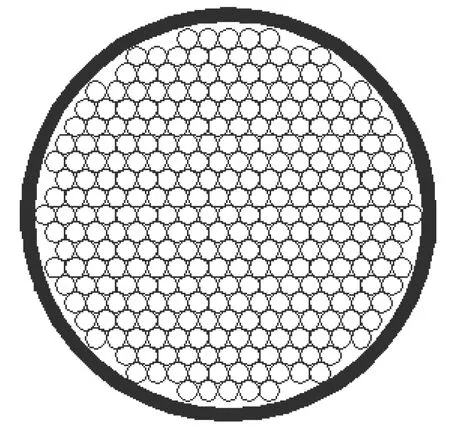
图1 单层破片排布方式

如图2所示,外弹道分成开舱前母弹和开舱后破片飞行段。破片弹幕与目标时空交汇,需满足火控弹道解算方程：

(1)

式中:dq为水平射击距离;Pq为航路捷径;q为航路角;Dq为射击斜距离;εq为高低角;fx、fy、fz为理想炸点在地面坐标系Oxyz[7]下的三坐标值,与火炮初速v0、射角θ0、开舱前母弹飞行时间tw、气象条件等有关;θc、ψc为开舱点处的速度高低角(弹道倾角)和速度方向角[7],当中口径火炮近距离射击时,ψc很小,该文假设ψc=0;Rp为火控弹道解算破片飞行距离即理想开舱距离;tf为火控弹道解算弹丸出炮口至交汇时间;tp为火控弹道解算破片飞行时间。

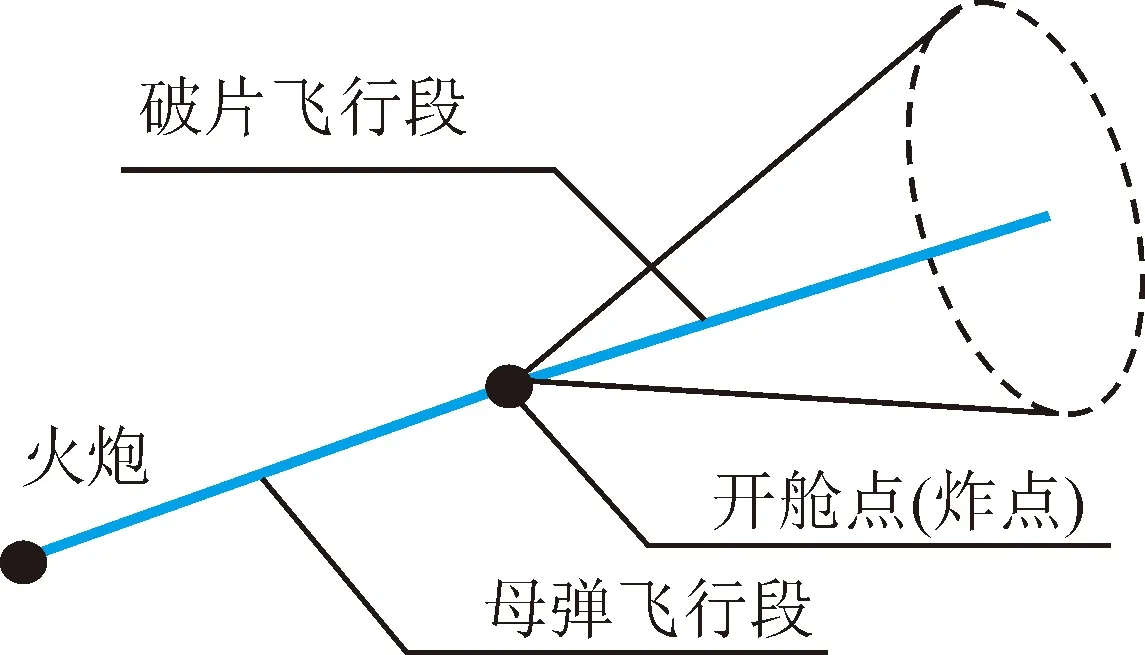
图2 破片飞行过程示意图

开舱前,破片与母弹以一定速度沿外弹道飞行,引信启动后,母弹舱室破裂,破片获得轴向和径向附加速度。对于整个破片群,各层及各圈破片距离开舱动力源的位置不同,层与层间的轴向速度以及各圈间径向速度产生差异。在研究破片运动规律时,假设:

1)破片飞行时间很短,不考虑重力作用;

2)破片径向速度较小,不考虑空气阻力对破片径向运动的影响;

3)母弹开舱为前开舱方式,外壳体向周向飞散,弹丸内预制破片向前飞出,弹丸开舱瞬间攻角为0;

4)破片保持良好的飞行稳定性,所有破片赋予相同的轴向附加速度。

在空气阻力作用下,Rp满足[8]：

(2)

2 破片命中毁伤模型

2.1 破片命中模型

建立目标坐标系Mqxmymzm,Mq为火控弹道解算理想目标提前点,Mqxm轴沿目标纵轴向前为正;Mqym轴垂直于Mqxm轴指向上方为正;Mqzm轴由右手法则确定。

建立误差坐标系Mqx3y3z3,Mqx3轴沿炮目连线方向,正向朝远;Mqy3轴垂直于Mqx3轴向上方为正;Mqz3轴由右手法则确定。

中口径火炮对空射击时,以弹丸出炮口为时间起点,设火控弹道解算tf时刻弹目交汇,弹幕中心破片与目标间的系统误差为

(3)

式中:μDq为距离系统误差；μεq为高低射角系统误差；μβq为方向射角系统误差。

tf时刻弹幕中心破片与目标误差的协方差阵为:

(4)

式中:σDq为距离均方差；σεq为高低射角均方差；σβq为方向射角均方差。

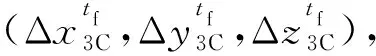
(5)

tw时刻为火控弹道解算开舱时刻,则Mqx2y2z2坐标系下炸点与目标偏差为:

(6)

近炸引信满足引信启动准则的理想炸点时刻为tw+ta,设引信产生的时间误差Δtc服从正态分布,数学期望为μtc,均方差为σtc,tc为引信误差抽样值。实际交汇时刻为tf0=tw+td+tp0,在Cx2y2z2坐标系下,弹幕中心破片与目标的偏差为:

(7)

式中:td=ta+tc;Rp0为破片飞行tp0时间的开舱距离;vm为目标飞行速度,该文假设目标水平匀速飞行。

破片命中模型为：

(8)

式中:RH0为破片飞行tp0时间的弹幕半径。破片在Mqy2z2平面内的散布近似为圆形,飞行tp0时间的散布圆半径为：

(9)

式中:vtmax为最外圈破片的切向速度,vtmax=ωcrpmax,ωc为开舱瞬间母弹角速度,可通过射表或解外弹道方程组获得；rpmax为最外层破片距离母弹中心半径。在引信启动准则下根据式(8)迭代可求得实际破片飞行时间tp0以及破片飞行距离Rp0。

2.2 破片毁伤模型

文中以某反辐射导弹为例,将其分为导引头、制导舱、战斗部、控制室、发动机室、弹翼、舵片等舱段,分别研究各舱段的毁伤情况,最后得到目标的毁伤。

弹幕中心破片与目标合成速度为:

(10)

式中:vp0为弹幕中心破片飞行tp0时间的速度,vp0=vpc/(Avpctp0+1)[8]。

根据目标毁伤理论,对柱形、棱柱形破片,可采用侵彻经验公式:

(11)

式中:vj为相对极限撞击速度;kv为试验系数,对硬铝合金kv=2 852;hj为第j舱段对应的等效硬铝靶板厚度;Sp为破片迎风面积;γj为破片相对速度与第j舱段法线的夹角。为简化计算,文中将导引头前端处理成半球体,其它主体部位舱段处理成等截面圆柱体。图3中Rm为目标截面半径,Lmj为第j舱段长度。

图3 舱室结构示意图

某反辐射导弹各舱室造成C1级毁伤的毁伤准则[6]如表1所示。

表1 反辐射导弹各舱室毁伤准则表

由于目标形状不规则,弹幕内不同破片与目标各部位交汇的γj均不相同。如图4所示,对于2～5舱段有:

(12)

式中:dmj为弹幕内任一破片飞行轨迹与第j舱段中心轴线间的距离。

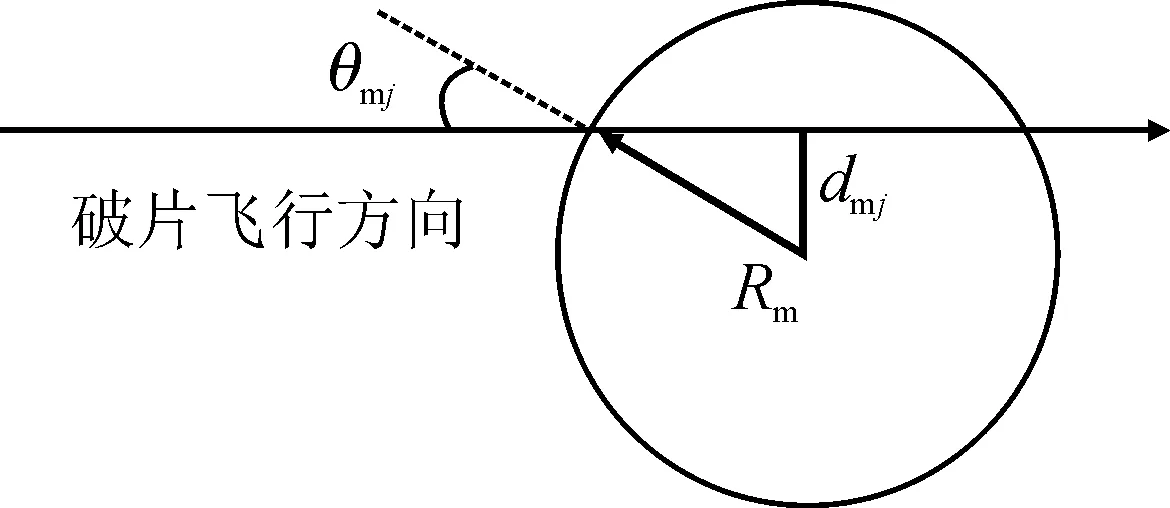
图4 破片与目标交汇示意图

在弹幕覆盖目标舱段前提下,由式(11)得破片相对速度与第j舱段法线极限夹角:

(13)

满足式(13)侵彻条件的破片飞行轨迹与第j舱段中心轴线间的极限距离:

(14)

有效毁伤面积在Mqy2z2平面内的投影:

(15)

对于导引舱前端即第1F舱段,破片相对速度与第1F舱段法线的夹角满足:

(16)

式中:dm1F为球心至弹幕内任一破片飞行轨迹的垂直距离。

γ1Fj的求解同式(13),球心至弹幕内任一破片飞行轨迹的极限距离:

dm1Fj=Rmsinγ1Fj

(17)

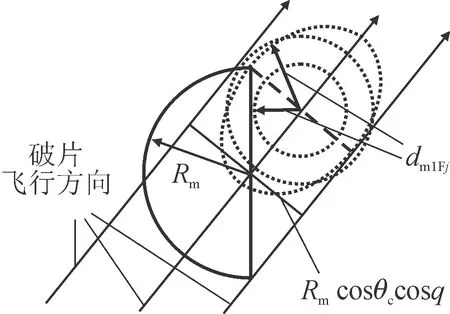
图5 投影面积示意图

如图5所示,当dm1Fj≤Rmcosθccosq,有效毁伤面积在Mqy2z2平面内的投影为:

(18)

当dm1Fj>Rmcosθccosq,有效毁伤面积在Mqy2z2平面内的投影为:

(19)

第1舱段有效总毁伤面积为:

Sc1=Sc1F+Sc1S

(20)

式中:Sc1S的计算方法可参考式(12)～式(15)。

当确定各舱段有效毁伤投影面积后,可得期望毁伤第j舱段的破片数目为:

(21)

第j舱段条件毁伤概率[6]为:

Gj=1-exp(-ncj/nsj)

(22)

式中:nsj为毁伤第j舱段所需破片数目(见表1)。

对整个导弹的条件毁伤概率为:

(23)

2.3 炸点位置的确定

由式(7)知,当tc的统计特性确定后,实际每发弹炸点位置主要由ta决定。文中将弹目相对姿态、相对运动速度、破片对目标的毁伤等信息融入引信启动准则,以毁伤概率最高作为确定引信启动准则的标准。图6为确定炸点位置的计算程序框图,±ta0为ta的边界条件,tp00为tp0的上边界条件。

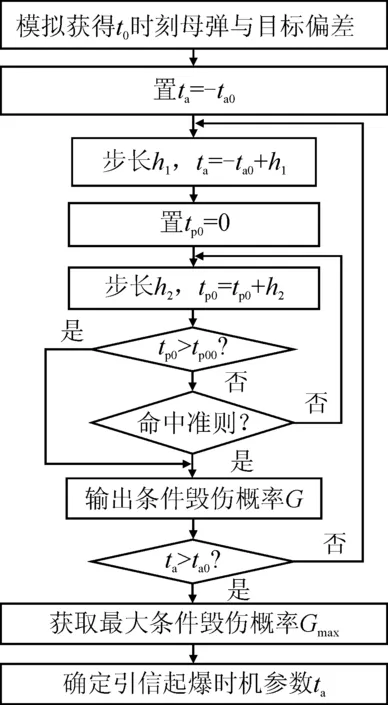
图6 计算引信启动时机的程序流程图

2.4 理想开舱距离的优化

由式(6)知,在其它条件确定时,tw时刻炸点与目标偏差受Rp或tp影响。图7为确定tp的计算程序框图,根据式(2)可求得Rp。

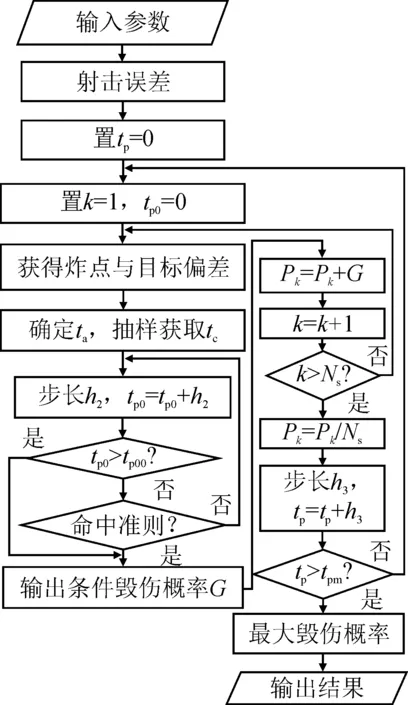
图7 开舱距离计算的程序框图

3 仿真及结果分析

3.1 仿真条件

μDq=0.4%Dq,μεq=4 mil,μβq=4 mil,σDq=0.6%Dq,σεq=6 mil,σβq=6 mil,dp=6 mm,mp=3.3 g,ND=301,np=6,NpD=1 806,va=600 m/s,rpmax=54 mm,vm=250 m/s,H=50 m,Pq=500 m,v0=900 m/s。μtc=1 ms,σtc=5 ms,Rm=0.25 m,Lm1=0.621 m,Lm2=0.555 m,Lm3=2.777 m,Lm4=0.819 m,Lm5=3 m,ρ=1.225 kg/m3,ρFe=7 800 kg/m3,ρp=18 170 kg/m3。

3.2 结果分析

图8为不同射击距离Dq下的毁伤概率Pk随破片飞行时间tp的变化曲线。由图8可知,随着tp增大,即Rp增大,实际弹目交汇时命中概率不断增大,命中概率的增大使毁伤概率增大,但随着Rp进一步增大,在满足命中准则时的破片侵彻能力不断下降,条件毁伤概率的下降使得毁伤概率下降。在给定仿真条件下,在tp=0.08 s附近中口径火炮对目标的毁伤概率最高。

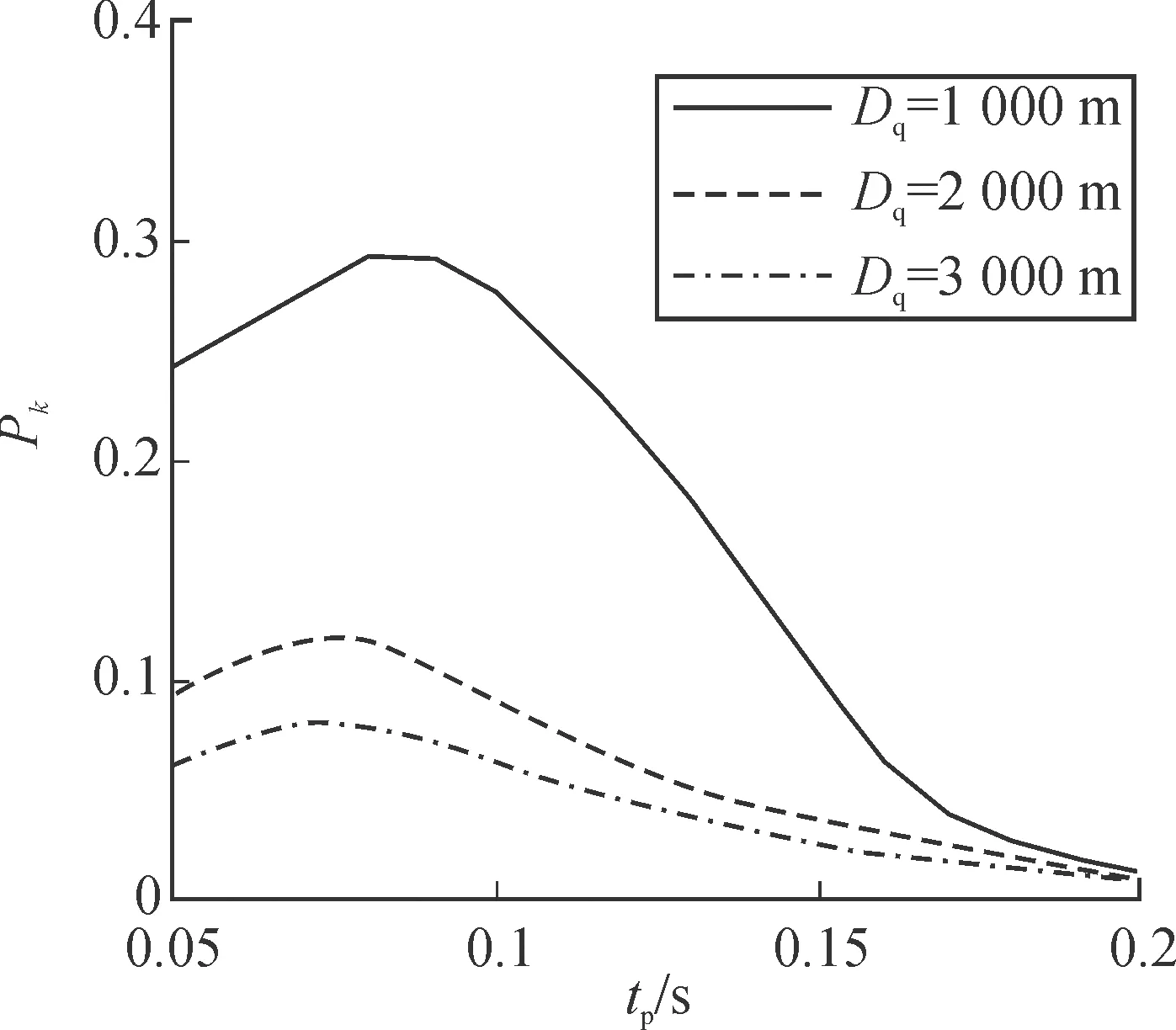
图8 毁伤概率随火控弹道解算破片飞行时间的变化曲线

图9为tp=0.08 s时,抽样获取几组弹幕中心破片与目标偏差下的条件毁伤概率G随开舱时机td的变化曲线。由图9可知,随着实际引信起爆时机的不断后移,弹目距离不断减小,弹幕破片密度不断增大,条件毁伤概率不断提高。当弹目距离进一步减小,无法满足命中准则时条件毁伤概率为零。

4 结论

该文建立了中口径火炮配备近炸引信发射预制破片弹对某反辐射导弹的射击效率模型,通过仿真计算得到了中口径火炮反导毁伤概率。研究结果表明:火控弹道解算存在一个最佳开舱距离,在解算射击诸元时通过优化开舱距离可提高反导毁伤概率;引信启动准则及引信工作误差对中口径火炮反导能力的影响很大,在一定引信技术支撑下中口径火炮发射预制破片弹近距离可具备较好的反导能力。

图9 条件毁伤概率随开舱时机的变化曲线