基于benford定律和面板模型判别上市公司违法违规行为有效吗
王泽霞,李正治
(杭州电子科技大学 会计学院,浙江 杭州 310018)
一、文献回顾及研究动机
上市公司舞弊历来是资本市场的监管难点,是审计理论界、实务界聚焦的重点,如何有效识别企业舞弊行为更是其中的关键点。国内外研究学者采用实证研究方法从公司治理特征、违法违规的诱因、预警和侦查等多角度对公司舞弊等违法违规行为进行了丰富的研究,实证研究表明模型舞弊识别效果较优。
现有舞弊识别模型主要有多元判别分析模型、logit模型、probit模型、人工神经网络模型、决策树、贝叶斯网络等,梳理发现模型识别的效率比经验识别效率高,其中logit回归模型的应用最常见,而从结果的准确性方面来看神经网络整体则优于回归模型。Kirkos和 Spathis(2007)[1]应用人工神经网络、决策树和贝叶斯网络三种算法建立会计舞弊检测模型。检测结果显示:贝叶斯网络模型的效果最好,准确率为90.3%,神经网络和决策树模型的准确率分别是80%和73.6%;陈国欣和吕占甲等(2007)[2]从上市公司中选取1994—2005年间舞弊公司和正常公司126家作为研究样本,从财务、股权结构、内部控制以及其他等四类29个指标构建Logistic回归模型,模型总体识别正确率达到95.1%,预测效果良好;洪文洲和王旭霞等(2014)[3]选取44家舞弊公司和44家财务报表正常的公司作为对比,选取两组样本中具有显著性差异的指标数据,构建向后逐步法的logit回归模型作为财务报告舞弊识别模型,模型整体的预测准确率达到了88.89%;王泽霞等(2017)[4]构建 BPLVQ的组合神经网络舞弊风险识别模型,研究结果表明:组合神经网络模型的识别率为90.56%,显著高于这两个单一神经网络模型的舞弊识别率。上述舞弊模型的研究也有其局限性,研究过程中训练样本和检验样本的选取按照舞弊和非舞弊1∶1进行配对,在对检验样本进行预测时,由于1∶1的配对原则,导致即使不选择使用模型,人工随机选取,识别率也能达到50%,因此已有研究文献中预测准确率往往存在被高估的可能性,同时在现有模型识别研究中,benford定律多运用于评价财务数据质量,在舞弊等违法违规的识别上尚不多见,因此本文重点探讨综合运用benford定律和面板模型来识别上市公司违法违规行为这一方法是否有效,提供一种新的舞弊识别模型来识别公司违法违规行为。
benford定律作为数学科学,已有研究学者从理论和实证上,证明了财务数据的分布客观上符合benford定律,因此运用benford定律和面板模型识别财务数据是否篡改造假,具有一定的理论基础。基于对已有文献的梳理,一般认为benford定律可以用来评价财务会计数据的质量,张苏彤和康智慧(2007)[5]利用benford定律对上市公司财务数据按总体、分板块和分行业分别进行测试,发现上市公司财务报表主要财务数据的首位数频率分布与benford定律所描述的首位数频率分布保持了高度的相关,上市公司公布的财务数据都较好地符合benford定律;赵莹和韩立岩(2007)[6]发现运用benford定律可以发现公司的轻微数据操纵行为和操纵者某些独特的行为文化特质,研究发现ST公司更倾向于篡改“偶数”进行利润操作,证实了benford定律可以有效运用于利润操纵侦测,同时运用Jones模型对研究样本进行稳健性测试,进一步证明了运用benford定律可以有效识别上市公司利润操纵行为;Nigrini and Miller(2009)[7]指出benford定律可以用来测试不同交易水平下会计数据的有效性和可靠性,并指出这种检测方法可以用于任何传统的分析复核程序无法轻易鉴别的数据;Charles E Jordan,Stanly J Clark(2011)[8]研究发现benford定律不仅可用于检查是否有假账,还可以用于会计、金融甚至选举中出现的数据;刘云霞(2012)[9]等在研究中探讨了如何将 benford定律与面板模型相结合,找出可能存在质量异常的具体问题数据的方法;杨君岐和王娇(2016)[10]采用benford定律,构建上市公司财务信息质量评级系统,检验结果表明benford定律能够很好地评价公司会计数据的质量;陈伟和吴正等(2017)[11]从大数据审计角度,研究bengford定律在电子数据审计中应用的可能性和基本的实现路径。
本文利用面板模型进行数据分析的基本原理是,可以用面板模型来拟合任何一个数据指标和与之相关的另一项或一组指标之间的关系。如果进行回归后,结果表明整体模型拟合得很好,只有少数几个数据点严重偏离既定模型,则很可能认为位于这些点(偏离点)上的数据准确性存在一定的问题,有必要作进一步的观察与分析。综合上文所述,基于benford定律良好的统计特性,对财务数据的分布进行检验,再结合面板模型找出具体位置和时间的异常数据点,方便注册会计师重点对“可疑”的上市公司深入调查,从而对提高审计效率,减少审计风险将是十分有效的。
二、benford定律和面板模型综合设计
(一)benford定律
1881年,美国数学家、天文学家Simon Newcomb,偶然发现对数表的第一页比其他页更破旧,针对这一现象经过大量的统计分析后,首先发现首位数概率分布,但是Simon Newcomb对于这一现象仅仅是出于好奇,并未做进一步研究。之后美国通用电器公司物理学家 Frank Benford(1938)[12]也注意到了这一现象,通过收集不同类型的数据共计20 229,涉及领域广泛包括电费账单、城市人口数量、湖泊的面积、物理以及数学领域中的常数、篮球比赛中的得分等,经过大量的实证研究,最终验证了Simon Newcomb的理论,研究发现,首位数为1的数字出现的频率是30.1%,首位数为2的数字出现的频率是17.6%,往后出现频率依次减少。美国学者Hill(1995)[13]从理论上对Benford法则给出了满意的解释,并进行了严谨的数学证明,同时发现,研究的数据量越大,结果越接近benford定律的理论分布。
Benford定律首位数出现的概率公式:

其中,首位数字n是指左边的第一位非零的有效数字。根据公式(1)首位数概率分布如表1所示。

表1 benford定律首位数概率分布
(二)benford定律的检验方法
目前有四类常用的检验方法,来验证样本数据的分布是否符合benford定律的期望分布。
下列检验公式中,ei是首位数是i的实际频率,pi是benford定律下的理论频率。Fe(x)是实际样本首位数的累积分布函数,Fp(x)是理论分布下的首位数的累积分布函数。
1.χ2拟合优度检验。χ2拟合优度检验是较为重要的检验方法:

在显著性水平为10%、5%和1%条件下,χ2的临界值分别为13.36、15.51和20.09。
原假设:实际样本首位数分布符合Benford定律的理论分布。
备择假设:实际样本首位数分布不符合Benford定律的理论分布。
若统计量大于临界值,则拒绝原假设,接受备择假设,表明该样本数据与benford定律理论分布不相符,样本数据质量值得怀疑,财务指标数据可能是人为篡改的。
2.修正Kolmogorov-Smirnov拟合优度检验。根据Kolmogorov-Smirnov检验理论,将实际样本首位数累积分布函数减去benford理论分布函数之差,取绝对值,并选取最大值作为统计D值,将D值与临界值进行比较,若大于,则说明实际样本首位数分布不服从该理论分布。
Stephens(1970)[14]对 K-S 拟合优度检验作了修正,检验方法如下:
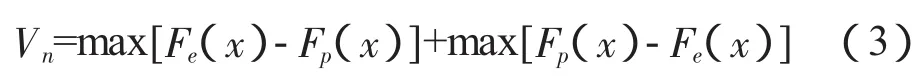
Giles(2007)[15]对公式(3)的统计量再作修正,方法为:
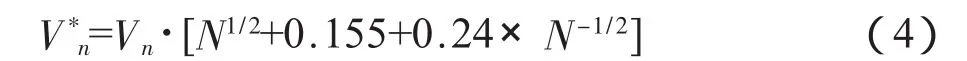
在显著性水平为10%、5%和1%条件下,V*n的临界值分别为1.19、1.32和1.58。
3.修正的距离检测。计算实际样本首位数的频率分布与benford理论分布之间的距离,其中距离越大越不符合benford理论分布距离计算公式:
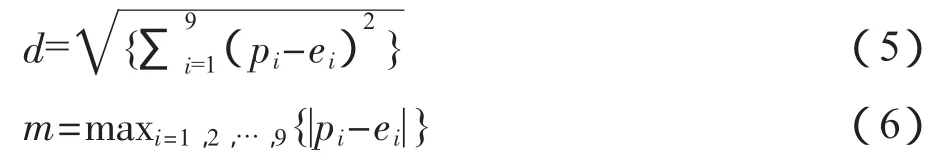
Morrow(2014)[16]对上述距离进行了修正:
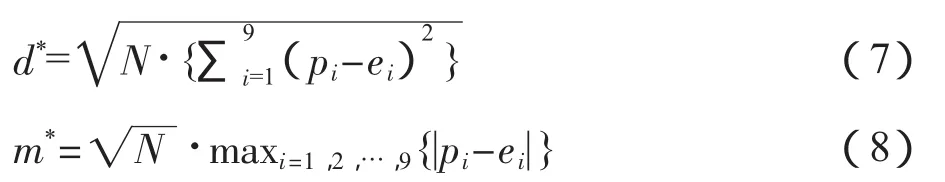
在10%、5%和1%的置信水平下,d*统计量判别值分别为1.212,1.330和1.569;m*统计量判别值分别为0.851,0.967和1.212。
4.Pearson相关系数。计算样本数据的首位数频率分布与首位数期望频率分布的Person相关系数,相关系数越接近于1,则越符合benford理论分布。

表2 benford定律检验方法
(三)benford定律和面板模型综合运用
在数理统计中,面板数据可以提供时间序列和截面两个维度上的数据信息,并把它们融合在一起。利用适当的面板回归方法,它不仅可以用于模拟自变量和因变量之间的关系,也可以用来观测样本中有差异的数据。在benford定律对数据进行分析的基础上,再构建面板模型进行拟合,进一步发现具体哪家公司、具体年份上的可疑样本点。
benford定律和面板模型结合的思路:(1)对研究样本中的各个财务指标数据进行首位数字测算,得出各财务指标首位数的频率分布;(2)将计算出的首位数字频率分布与benford定律首位数的期望分布进行统计学检验和分析,判断两者之间差异是否显著,具有显著差异的则很可能是存在异常的财务指标数据;(3)运用面板模型对很可能存在异常的财务指标数据进行回归模拟和残差分析,如果模型拟合效果较好,仅存在极少数样本点偏离回归模型,表明大多数样本符合预期,而偏离的样本点则可能存在问题;(4)根据残差分析,得到的“异常样本池”,再查阅证监会、财政部等网站以及媒体报道,找出历史会计年度是否存在舞弊行为或违法违规事项,进行结果的验证。
三、实证检验
(一)数据来源与变量选取
实证分析采用的数据来自国泰安数据库,所选择的样本为2006—2016年间全部A股上市公司的年度财务报表数据,根据已有文献研究,资产负债表中选择应收账款净额、资产总计、负债、资本公积、未分配利润、所有者权益合计;利润表中选择营业收入、营业成本、销售费用、管理费用、营业利润、利润总额、净利润,共计13个指标。针对样本结果的分析,则参考证监会、财政部、深圳证券交易所和上海证券交易所等平台发布的公告信息。
(二)财务指标首位数频率分布及benford定律的检验分析
1.财务指标首位数频率分布。表3给出了在剔除了缺失值后全部A股2006—2016年间主要财务数据指标的首位数分布情况。表3中各项财务指标数据首位数频率分布基本上都较好地符合benford描述的首位数频率从1到9依次递减的规律,证实了前文梳理的研究文献中关于benford定律可以应用于评价财务数据质量的研究结果,同时依表3看出实际的频率分布与期望分布存在一定程度上的差别,但是是否具有显著差异,还需要进行本文下一步的统计检验分析。
2.benford分布的检验分析。根据表4,可以将下述13个财务指标划分为严重偏离、一般偏离、相对符合三个组:(1)严重偏离组:资产总计、资本公积、所有者权益合计和管理费用;(2)一般偏离组:应收账款净额、未分配利润和净利润;(3)相对符合组:负债、营业收入、营业成本、销售费用和营业利润。
第(1)组和第(2)组的财务指标基本上在1%显著性水平上都拒绝原假设(χ2、V*n、d*和 m*统计量,除应收账款净额的χ2统计量之外),与原假设具有显著差异,有理由认为其不符合Benford分布,但是第(1)组统计量值明显大于第(2)组统计量值,认为第(1)组偏离更为严重。第(3)组财务指标(除负债的V*n统计量以及的销售费用的V*n统计量之外)至少在1%显著性水平上没有拒绝原假设,有理由认为其具有较高可能符合Benford分布。
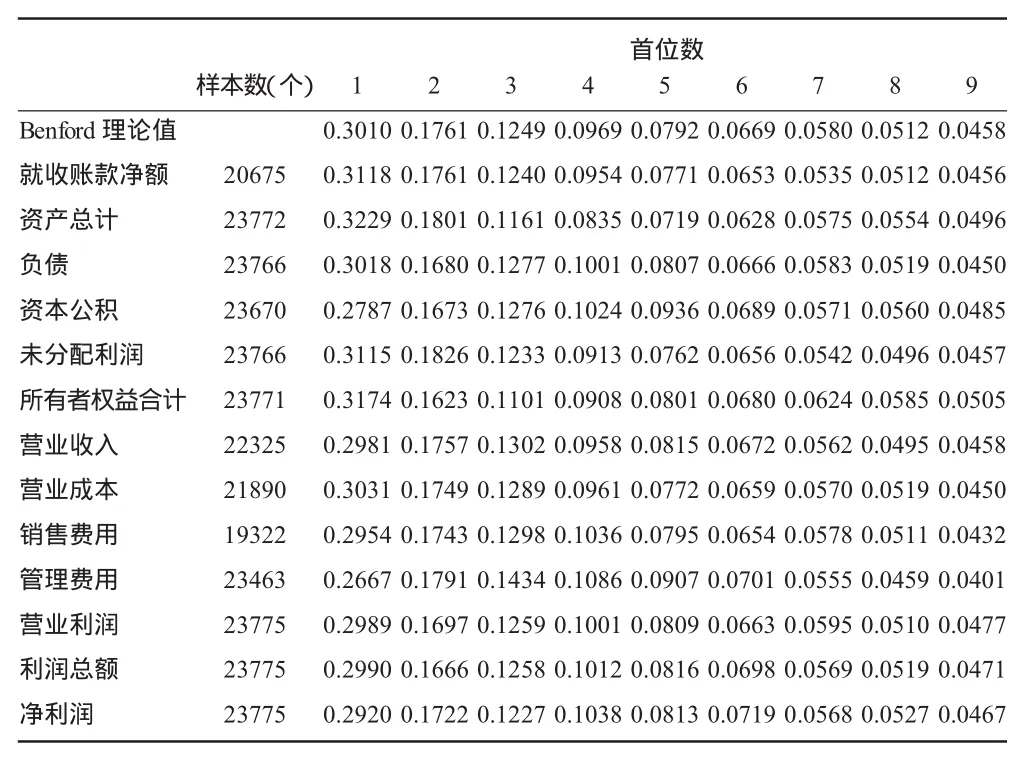
表3 样本数据测试结果
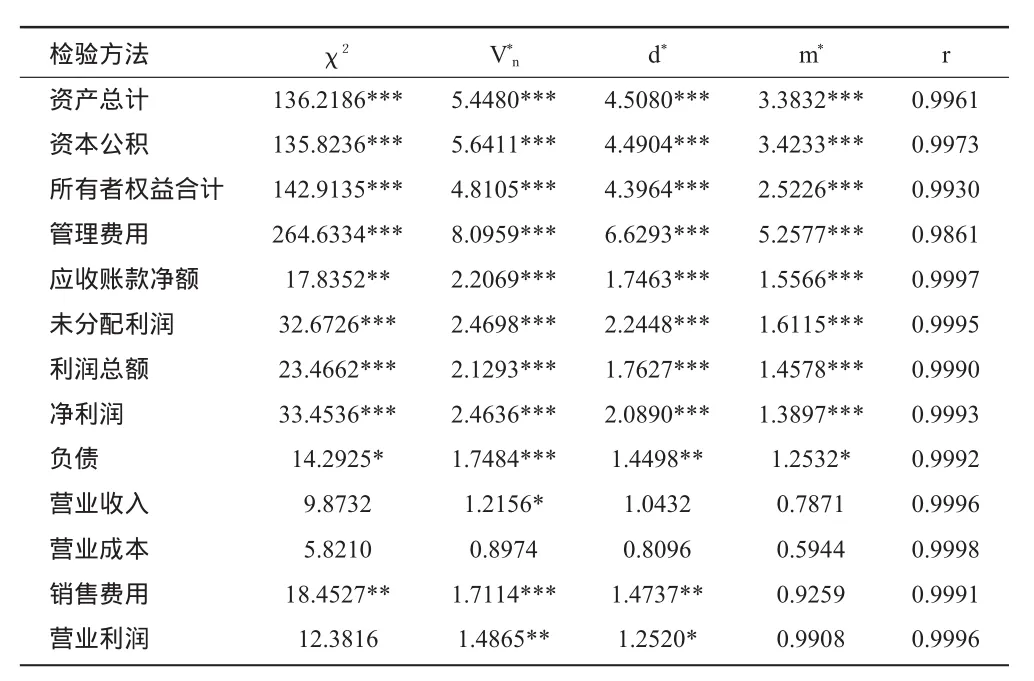
表4 样本数据拟合优度检验结果
(三)建立面板数据模型
1.模型构建。面板模型构建思路:(1)被解释变量选取差异最大的指标即将上述的严重偏离组中的财务指标都作为候选的被解释变量;(2)解释变量选取差异最小的指标即将上述的相对符合组中的财务指标都作为候选的解释变量,由表6解释变量相关系数矩阵看,各解释变量之间相关性比较高,为避免多重共线性,每次只选择一个指标进行拟合。从本文主要目的是筛选数据存在问题的公司这一角度来看,这种处理方法是合适的。
经过筛选,资产总计(Total Assets)和管理费用(Administration Expenses)作为被解释变量,解释变量有负债(Liabilities)、营业利润(Operating Profit)、营业收入(Operating Revenue)和营业成本(Operating Costs),具体模型如下:

其中,各变量含义:i=1,2,3,…,即样本中每一家公司;t=1,2,3,…,11,即 2006—2016 年的每一年;Total Assetsit和 Administration Expensesit分别为第i个公司在第t年的资产总计数额和管理费用数额;α、β和μit分别为截距项、斜率系数和随机误差项。
我们利用广义最小二乘法对上述模型进行估计。从表5回归结果看,各个模型的截距项和斜率系数均非常显著,并且各个模型的R2都达到了0.9以上,可以认为模型整体拟合效果较好,为下一步残差分析提供较好的基础。
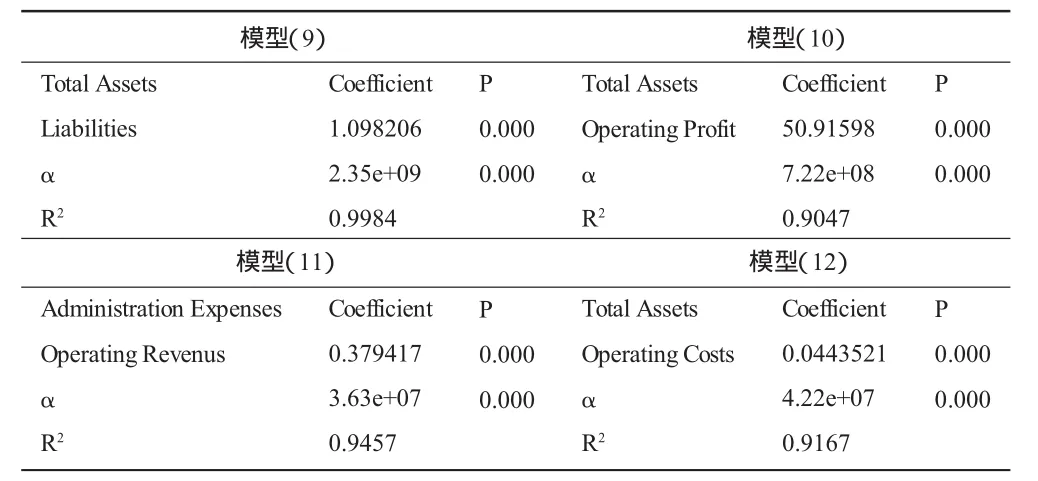
表5 模型回归结果
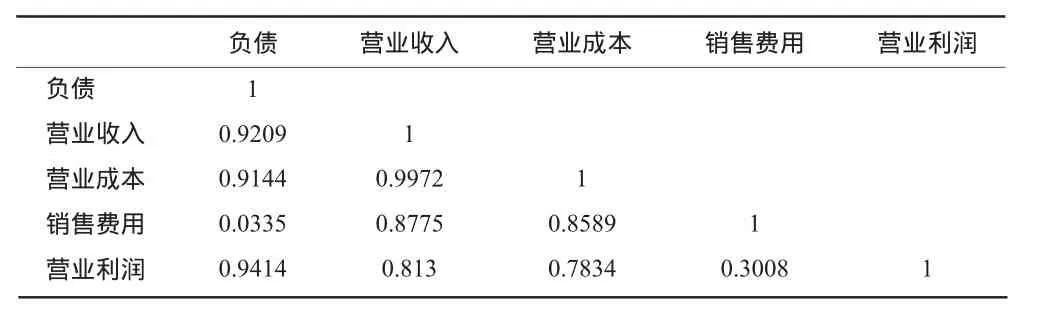
表6 各解释变量相关系数矩阵
2.残差及结果分析。在面板模型中,残差分析所提供的信息可以用来对数据进行诊断。如果面板模型可靠,拟合良好,可以将残差视作误差的预测值。标准化残差服从标准正态分布N(0,1),如果样本的标准化残差落在(-2,2)之外,则可以在95%的置信区间内视作异常数据点,这些样本数据点更有可能出现质量问题。
根据2006—2016年的残差数据,计算每家公司每年残差的标准化数值:

其中,Zij为第i年第 j个公司的标准化残差值;xij为第i年第j个公司的残差;为第 i年所有公司残差的平均值;σi为第i年所有公司残差的标准差。
根据现有文献分析,发现舞弊或违法违规的时间有可能并不是真正的舞弊或违法违规的起始时间,以前年份的舞弊或违规行为可能由于公司手段高明隐晦、金额较小或者性质较轻而未被发现。连竑斌(2008)[17]研究发现上市公司舞弊有以下特点:时间跨度较长,在两年甚至两年以前上市公司就已经开始进行舞弊和违法违规操作,同时在该持续时间内,也会陆续有性质较重或者较轻的违法违规行为;从舞弊和违法违规行为实施到政府相关机构进行查处的时间间隔比较长,有的企业在违规操作两年后受到处罚,甚至有的企业是在五年后才被发现和处罚。章立军(2009)[18]研究发现舞弊与处罚的时间间隔大多数在两年以上,且舞弊具有较大的隐蔽性。龙凤(2012)[19]对研究样本检查发现,舞弊行为发生在一个年度内大约占比9%,持续时间两年占比42%,持续三年占比21%,舞弊行为发生大于等于四年的达到28%以上,最长的甚至达到9年。
因此本文不考虑违法违规行为实施的具体年份,在此情况下对预测结果进行分析:模型预测的异常值公司共56家,有效预测公司共29家,识别率达到51.79%。连竑斌(2008)对国内上市公司舞弊的研究文献整理后,指出实施舞弊或违法违规行为的公司,通常会采用“隐蔽”的方式进行财务报表粉饰,使得注册会计师在实施审计时不容易发现,同时,也有一定数量的公司会选择与注册会计师沟通,对相关会计处理进行调整,从而降低金额或减轻性质的严重程度,以获取“无保留意见”的审计报告,因此在舞弊和违规本身“隐晦”和难以及时发现,且本文的研究样本量达到2万以上(每年每家公司视为一个样本的话)数据规模庞大的情况下,识别率达到了51.79%,这足以说明Benford定律与面板模型相结合的数据质量检测方法具有一定的真实性和可靠性,可以作为计算机辅助审计手段中的一个方法。
四、结语
本文选取2006—2016年全部A股上市公司13个财务报表指标,利用benford定律进行质量检验和分析,同时构建面板模型进行拟合。结果显示259个异常样本点上,有40个样本点的公司在预测年份前后两年内有舞弊或违法违规行为;在不考虑具体时间情况下,残差分析得出的56家异常公司有29家确实有舞弊或违法违规行为。
影响实验结果的因素有,首先多数上市公司违法违规行为会跨越数年,倾向于在该时间跨度内进行多次但性质不严重的违法违规行为,对财务数据进行金额不重大、性质不严重且比较隐晦的人为篡改,并不会选择在某一年度集中爆发,从而容易造成模型对轻微的数据篡改识别效果不明显甚至不能识别;其次本文是对财务指标进行首位数频率分布进行统计并检验分析后,选出最可疑的指标作为面板模型的被解释变量,构建面板模型拟合优度都达到0.9以上,但是并不能完全保证这些财务指标是上市公司常用的实施违法违规行为而改动的数据;最后,由于舞弊违规行为本身具有复杂性、隐蔽性和动态性的特点,未被发现违法违规行为的公司并不能证明该公司没有进行过违法违规行为,基于以上因素的考虑,识别率51.79%,仍表明benford定律和面板模型相结合的方法具有一定的应用价值。

