基于模糊AHP的机械专业实验教学质量评价体系研究

谢淮北

(安徽理工大学 机械工程学院,安徽 淮南 232001)

在实验教学质量评价方面，人们研究的重点在于构建评价体系。然而，侧重于评价方法的研究报道相对较少。文献[1]指出采用单一方法评价主题会导致评价结果认可度低。实验教学评价涉及的问题包含多个目标决策，目前，普遍采用的评价方法包括灰色聚类法、主成分分析法(principal components analysis，PCA)、层次分析法(analytic hierarchy process，AHP)、模糊评价法[2-5]等。在多元定性因素和多元定量因素影响下，实验教学质量的评价指标及其评价结果是多元化非线性关系[6]。因此，探寻规范性好、合理性佳、科学性优和操作性高的方法，能更好地反映出实验教学质量评价体系。如何将实验教学质量评价体系中定性的问题转化为定量的问题，探究出影响实验教学质量评价体系中各项指标总权重大小及其排序关系，对提高实验教学的质量具有指导示范的作用。本文提出采用层次分析法，探讨规范、合理、科学和公正评价实验教学质量。

1 AHP评价模型的建立

人们常遇到由众多复杂因素构成而又缺少定量数据的系统，这些系统往往涉及社会学、经济学和管理学等领域，采用层次分析法(AHP)在解决众多复杂因素构成而又缺少定量数据的问题中具有独特的优势。

1.1 建立层次结构

在采用层次分析方法建立问题层次结构之前，将问题按照逻辑顺序依次采用“冒泡法”构造出单个具有层次特性的结构模型，各层单个结构模型分别根据结构模型的评价目标和结构模型的影响因素分为多个层次，根据评价目标及各影响因素，将它们划分为目标层、准则层和指标层等多个层次。

1.2 构造判断矩阵

判断矩阵是以每两个方案(或子目标)的相对重要性为元素的矩阵，它是层次分析法的核心，对后期评价的结果具有重要作用。

构建层次模型后，为了获得判断矩阵，要以各层内单个元素与其他元素作为比较对象，将两个对象进行相对重要性比较。判断矩阵再经层次分析法确定相应的权重，采用1～9标度法，通过专家论证，将两两指标之间互相比较构成的判断矩阵，对于判断矩阵A中元素aij可以按如表1所示方法确定。

表1 模糊层次分析法判断矩阵的取值

对于两两比较所得的判断矩阵A=(aij)n×n，应满足如下性质：

①aij>0；

②aji=1/aij(i,j=1,2,,n)；

③aii=1。

当：

aij×aji=aik(i,j,k=1,2,,n)

(1)

成立时，矩阵A被称为一致性矩阵。

1.3 层次单排序及一致性检验

1.3.1层次单排序

判断矩阵A对应于最大特征值λmax的特征向量W，经过归一化处理后即为同一层次相应因素对于上一层次某因素相对重要性的排序权值，这一过程称为层次单排序。

判断矩阵权重采用特征向量法中的和积法确定。

1)将判断矩阵中各列进行归一化处理。

(2)

2)对式(1)中归一化后的矩阵将按行进行相加，有：

(3)

3)然后对式(2)中所得向量进行归一化处理，有：

(4)

最后，求得相应的特征向量Wi。

4)得出判断矩阵最大特征根为：

(5)

式中，AWi为向量AW第i个元素。

1.3.2层次单排序的一致性检验

对判断矩阵进行层次单排序的一致性检验。

1)计算一致性指标:

(6)

式中，n为判断矩阵的阶数。

2)查找相应的平均随机一致性指标RI，当n=1,2,,9，可通过表2查得。

表2 平均随机一致性指标

3)计算一致性比例：

(7)

判断矩阵的CR值高低决定判断矩阵一致性的优劣。CR越小，表示判断矩阵的一致性越好。当CR≥0.1时，需要按照上述步骤，重新根据实际排查情况结果，对判断矩阵进行系统性的修改。

1.4 层次总排序及一致性检验

设上一层包含有A1,A2,,Am共m个元素，层次总排序权重依次为a1,a2,,am；下一层次包含有B1,B2,,Bn共n个因素，单排序权重分别为b1j,b2j，,bnj。则目标层的总排序权重组合为：

(8)

则B层总排序中的随机一致性比例为：

(9)

当CR<0.10时，层次总排序结果具有较满意的一致性。

2 模糊AHP在机械专业实验教学评价体系研究中的应用

2.1 模糊AHP在机械专业实验教学评价体系模型建立

评价指标要符合卓越工程教育专业认证的要求，结合学校特色实验教学组织的特点，保持传统实验教学的优势。评价指标要在现有的基础上借鉴国内外已有的先进经验，这些经验中不单涉及实验教学管理方面，还涉及实验教学质量评价方面。结合机械专业实验教学的复杂性和主观性等特点，遴选归纳出符合机械专业实验教学评价指标体系，主要包括实验教学准备、实验教学过程、实验考核及教学效果4个主要方面，每类指标包含相应的子指标。

依据上述4个方面构建了实验教学的评价体系的层次模型。值得注意的是：实验教学的评价指标体系中每个方面的指标包含与之相对应的子指标因素。具体指标特征描述，如图1所示。

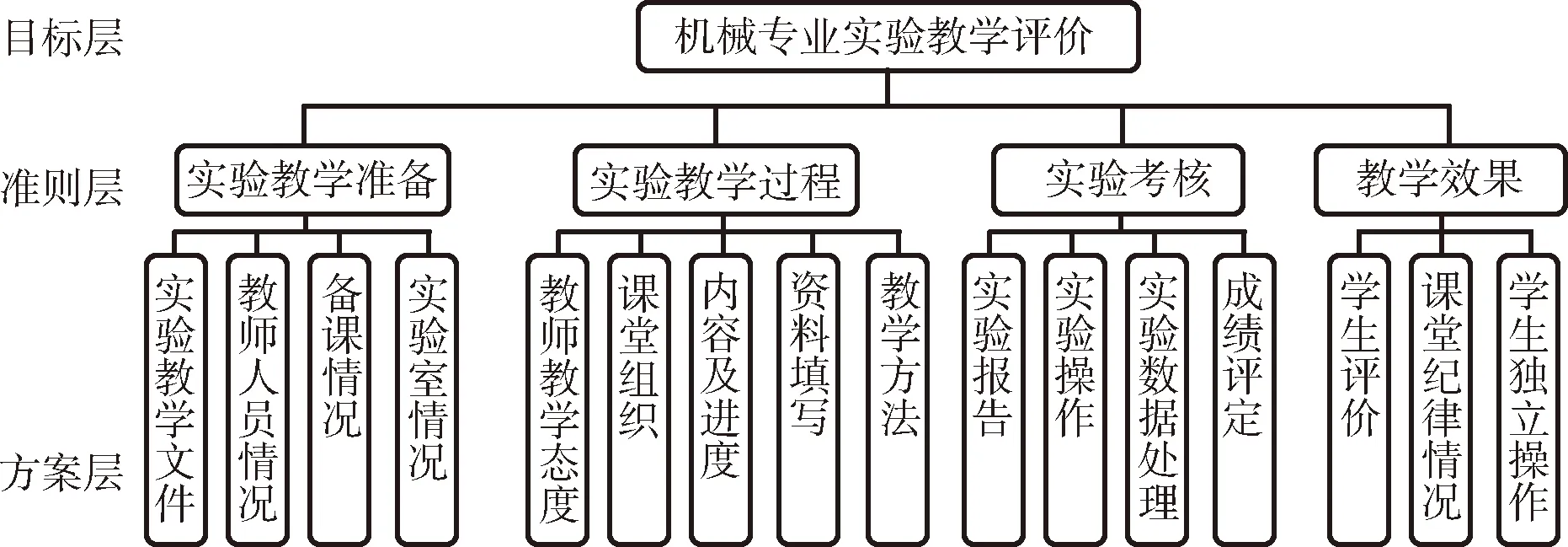
图1 层次结构图

2.2 模糊AHP在实验教学评价体系模型求解2.2.1 实验教学指标评估判断矩阵

根据图1的层次结构，结合表1的相关指标的度量值，按照两两判断矩阵的生成方法与结构形式，可以分别得到下层指标对上层指标两两比较的判断矩阵：

2.2.2层次单排序及一致性检验

在单一准则下，对于矩阵A，运用特征向量的和积法，分别得出教学评价指标体系的相对权重和教学评价指标体系的一致性检验。

1)首先，将矩阵的每一列进行归一化，得到矩阵：

2)然后，将所得矩阵按行相加，得到：

M0=0.26571.52040.76021.4537

3)将向量Mi进行归一化处理，得到：

W0=0.06640.38010.19000.3634

4)得到判断矩阵的最大特征根λmax=4.0042。

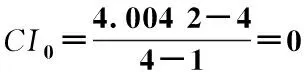
(10)

同理可得，通过判断矩阵计算指标权重的结果及其一致性检验数值如表3～表6所示。

表3 实验教学准备的指标权重

解出表3中的判断矩阵，得到λmax=4.2348，CI1=0.0781，RI1=0.90，CR1=0.0868。

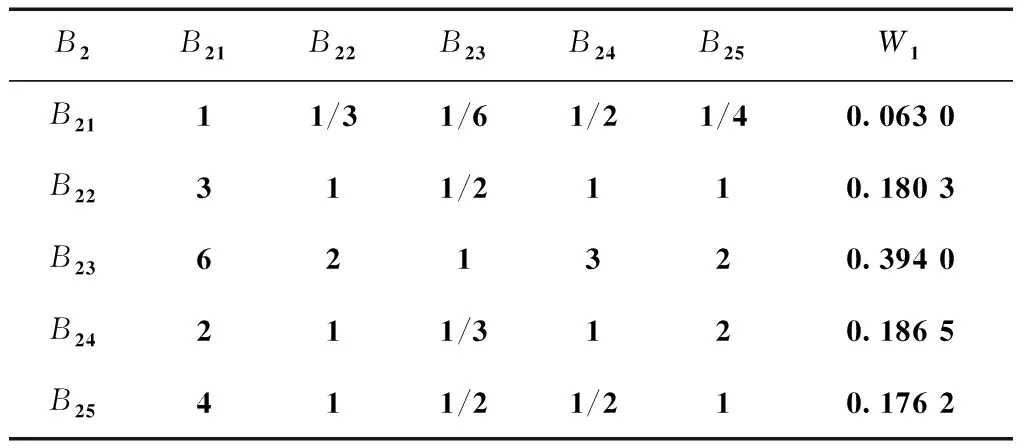
表4 实验教学过程的指标权重

解出表4中的判断矩阵，得到λmax=5.1708，CI2=0.0427，RI2=1.12，CR2=0.038。

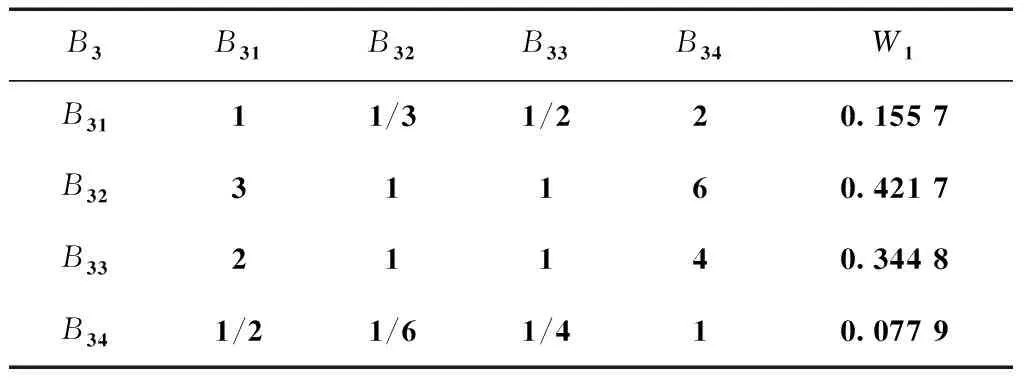
表5 实验考核的指标权重

解出表5中的判断矩阵，得到λmax=4.0206，CI3=0.0069，RI3=0.90，CR3=0.0076。

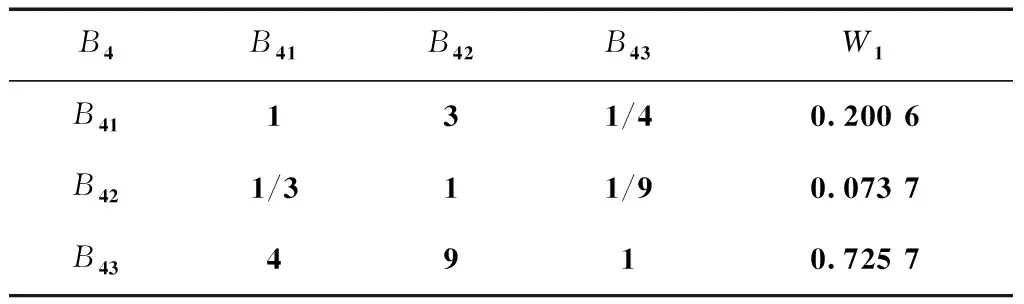
表6 教学效果的指标权重

解出表6中的判断矩阵，得到λmax=3.0092，CI4=0.0046，RI4=0.58，CR4=0.0079。

根据上述计算结果，每个指标的判断矩阵所对应的CR值均小于0.10，故全部通过一致性检验。否则，需要对矩阵重新赋值计算，最终得出每个矩阵的权重和CR值。

2.2.3层次总排序及一致性检验

利用上述构建的评价模型，对机械专业实验教学体系进行综合评价，得出各指标的组合权重，结果如表7所示。

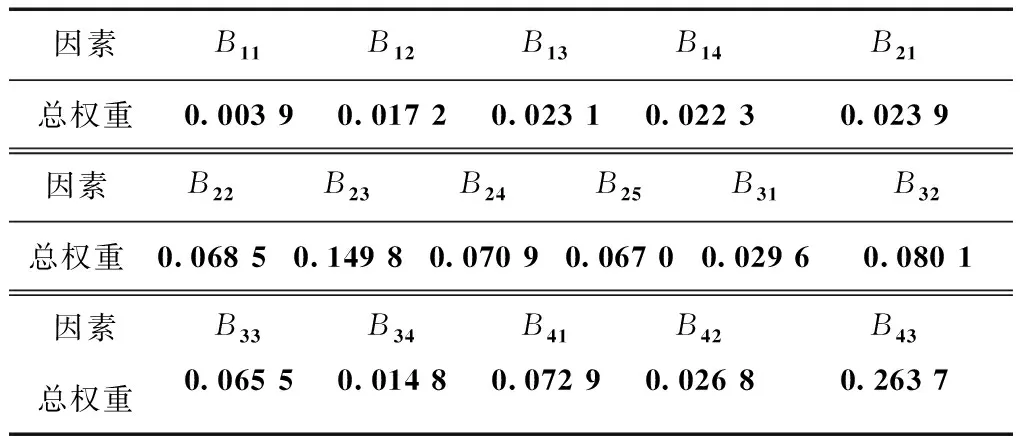
表7 各指标的组合权重

由于总排序随机一致性比例为：

(11)

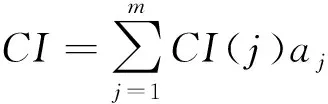
2.3 模糊AHP在实验教学评价体系模型验证

根据上述各因素指标的组合权重，对机械专业实验教学体系中实验教学设备等4个方面内容进行分配，在学院机械设计制造及其自动化专业10个班级进行了运用，并通过发放随机调查报告进行跟踪调查。结果显示，学生和教师评价较好。

3 结束语

通过创设建立层次模型，采用层次分析方法对实验教学质量进行系统性综合评价，结合机械专业实验教学体系的特点和卓越工程教育认证的要求，系统设计了实验教学质量评价指标，将定性问题转化为定性与定量相结合的问题，客观地构造出各指标的判断矩阵，通过层次总排序及一致性检验，可以得出指标层的每个因素的权重大小排序情况，根据分析结果系统分配学院机械专业实验4个方面因素占有权重，经试验后，学生和教师评价较高。这种评价方法简化了分析过程，提高了决策效率，不仅为机械专业实验教学质量的综合评价提供了方法，而且为教学管理人员提供了科学的参考依据。本文的评价模型可以推广到其他复杂的专业课程的教学质量评价中。