CT系统的参数标定及成像方法研究
夏彬珂,李天昊,邓明兴,,覃思义
(1.电子科技大学 英才实验学院,四川 成都 611731;2.电子科技大学 电子科学与工程学院,四川 成都 611731;3.电子科技大学 数学科学学院,四川 成都 611731)
电子计算机断层扫描(CT)[1]可以在不破坏样品的情况下,利用样品对射线能量的吸收特性,对生物组织和工程材料的样品进行断层成像,由此获取样品内部的结构信息。在典型的二维[2]CT系统中,平行入射的X射线垂直于探测器平面,每个探测器单元可看成一个接收点,且等距排列。X射线的发射器和探测器相对位置固定不变,整个发射-接收系统绕某固定的旋转中心逆时针旋转180次。对每一个X射线方向,在具有512个等距单元的探测器上测量经位置固定不动的二维待检测介质吸收衰减后的射线能量,并经过增益等处理后得到180组接收信息。
CT系统安装时往往存在误差,从而影响成像质量,因此需要对安装好的CT系统进行参数标定,即借助于已知结构的样品(称为模板)标定CT系统的参数,并据此对未知结构的样品进行成像[3]。
CT系统参数的标定是利用探测单元测得的信息重建精确图像的基础。基于标定后的CT系统主要参数,即可根据探测单元接收的信息准确构建未知介质的图像并获取相关信息。难点在于根据标定模板的吸收率以及模板的接收信息反推出CT系统的相关参数。这就需要建立CT系统的标定模型,标定CT系统的旋转中心点、探测器单元之间的距离以及该CT系统使用X射线的180个方向,进而利用这些标定的参数进行后面CT图像的重建,获取未知介质的相关信息。
本文利用X射线在介质中的衰减规律以及CT图像重建的相关知识,建立了CT参数标定的单目标拟合优化模型以及CT成像的滤波反投影图像重建模型。首先结合X射线在介质中的衰减规律以及Radon变换的相关理论,基于最小二乘原理建立单目标拟合优化模型。在求解上采用分组优化的方法,利用遗传算法对旋转中心点以及探测单元间距进行分组优化多次求解,求解结果基本收敛于同一数值。之后在标定的CT系统参数下,结合CT图像重建相关知识,运用傅里叶变换以及傅里叶切片定理,建立了CT图像的滤波反投影图像重建模型,基于探测器单元的接收信息,求解图像重建模型得到了正方形托盘上各个位置的吸收率信息,并构建出了介质在托盘上的位置和形状。最后通过对原数据信息进行图像重建和对比,验证了模型的可行性。
本文解决的问题来自2017年高教社标全国大学生教学竞赛本科组A题,文中所提及的“问题一”“问题二”,以及“附件1”“附件2”等信息请参阅该题目信息。
1 CT系统参数标定模型
在本模型中,已知标定用模板的几何形状和吸收率数据,且若已知CT系统的旋转中心和旋转角度以及探测单元的位置,则可以通过Lambert-Beers定理计算接收到的射线能量。然后将探测器接收到的信息乘上系统的增益因子,即可得到系统最后反映出的接收信息。现已知CT系统在180个未知方向上的接收信息,所以将CT系统旋转中心的坐标、180个方向的角度以及探测单元的间距作为决策变量,利用题目附件2的数据,通过最小二乘法建立损失函数。将最小化该损失函数作为优化目标,利用遗传算法求解决策变量的值。
1.1 探测器实际接收信息的计算
对于具有旋转效果的二维平面束CT系统,其系统结构可抽象为如图1所示。
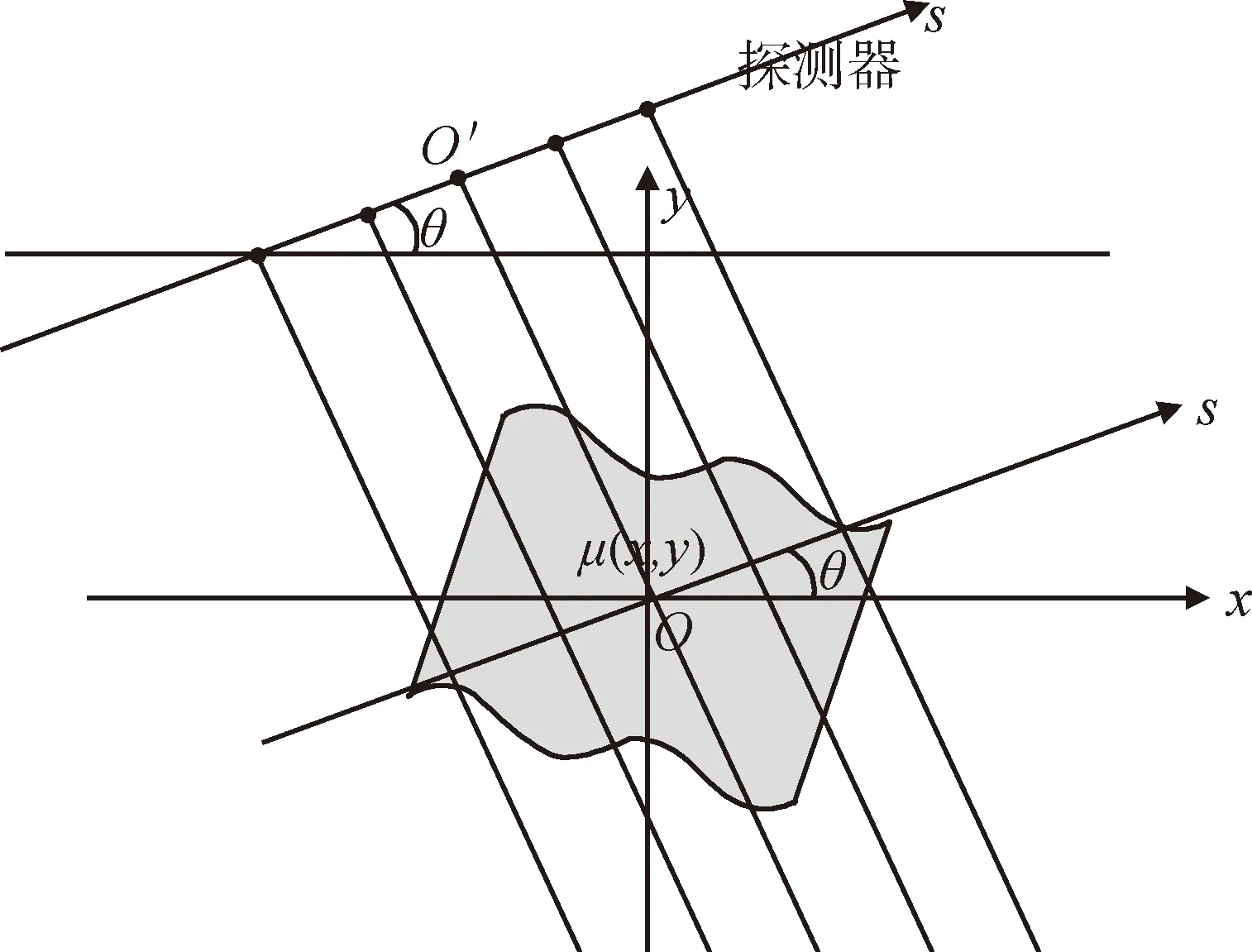
图1 平行束CT扫描示意图
图1中s轴为探测单元所在的一维坐标轴,可绕旋转中心旋转。其坐标原点为过旋转中心与作s轴的垂线与s轴的交点,易知该点落在第256与257个探测单元中间。由此,那么从左至右第i个探测单元在s上的坐标为[4]:
(1)
式中,d为探测单元之间的距离。
当CT系统的旋转中心与介质物体坐标系的坐标原点重合时,若CT系统当前的旋转角度为θ,则经过s轴上s点的探测线方程可记为:
s=xcosθ+ysinθ
(2)
由X射线吸收规律可知,CT系统旋转角度为θ时,第i个探测器接收到的X射线衰减信息可记为[5,6]:
p(si,θ)=∬μ(x,y)δ(xcosθ+ysinθ-si)dxdy(3)
式中,μ(x,y)为介质物体在点(x0,y0)处的吸收率。而当CT系统的旋转中心点与坐标系坐标原点不重合时,记旋转中心点在该坐标系中的坐标为x0,y0),经坐标变换后可得:
psi,θ=∬μx-x0,y-y0δ[(x-x0)cosθ+
(y-y0)sinθ-si]dxdy
(4)
1.2 最小二乘拟合优化模型
题目附件2中的数据反映的是经过增益处理后X射线衰减信息。假设增益处理都是线性的。对于得到的第i条射线在第j次旋转中穿越介质物体的总吸收率pij,pij=p(si,θj)引入增益因子λ,使λpij与题目附件2中的数据具有相同的含义,反映的结果为系统最终输出的接收信息。在此基础上基于最小二乘原理构建损失函数:

(5)
式中,tij表示第i个探测单元在第j次旋转中测得的经过增益等处理后的信息,即题目附件2中的第i行第j列数据。
以使该损失函数最小为目标,建立如下优化模型:
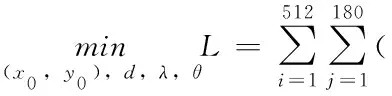
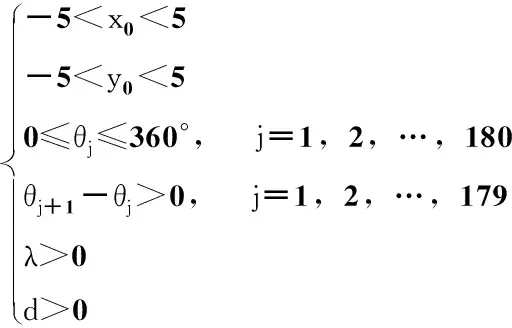
(6)
式中,(x0,y0)为CT系统旋转中心点的坐标,θj为CT系统第j次旋转的旋转角。优化模型的决策变量为x0,y0,λ,d,θj(j=1,2,,180)。式中pij=psi,θj,其计算公式为:
pij=∬μx-x0,y-y0δ[(x-x0)cosθ+
(y-y0)sinθ-si]dxdy
(7)
1.3 标定模型求解方法
针对问题的实际情况对以上拟合优化的模型进行了适应性的求解预处理,包括:
1)对原始图片通过双线性插值[7]将像素从256×256扩增为1024×1024,增加求解的精度;
3)对接收信息数据进行等距分组,以30个旋转角为一组的组内间距将所有数据分为30组,每组含有6个旋转方向。通过减少每次优化求解的决策变量个数,以减少求解运算的复杂度;
4)通过对接收信息数据的分析,减小旋转角的约束范围,使求解时结果能更快的收敛到最优解。
最后,我们针对问题一进行适应性修正后的拟合优化模型为:
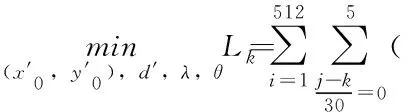
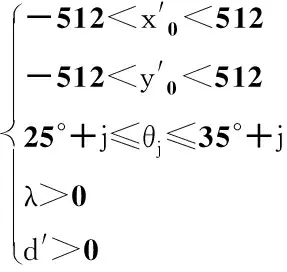
(8)
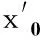
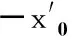
(9)
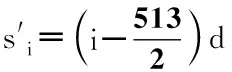
考虑到模型中有10个变量进行优化时变量仍较多,故采用对多变量优化问题表现良好的遗传算法[8]进行求解。遗传算法将变量进行编码转化为基因序列,通过模拟自然界繁衍、淘汰的规律对目标函数进行优化,最终得到一个较优的种群和最优解。下面以第一组数据为例,对遗传算法的求解过程进行解释。
求解时采用实数编码,种群个数为200,迭代次数为500,利用MATLAB[9]遗传算法工具包进行求解。
1.4 求解结果
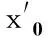
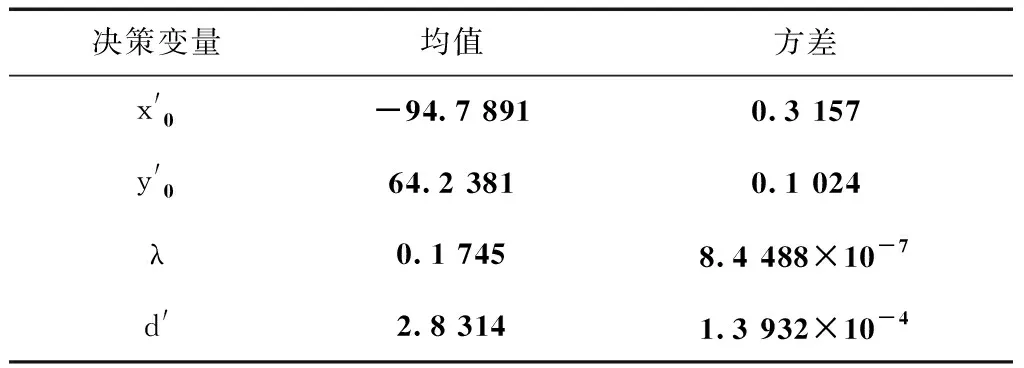
表1 标定模型求解结果
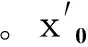
x0=Δ0(-64)=-9.2773mm
y0=Δ0×95=6.2500mm
d=Δ0×2.8314=0.2765mm
式中,Δ0为一个小单元格的宽度。故CT旋转中心在正方形托盘中的位置坐标为(-9.2773,6.2500)mm,即距托盘中心点左偏9.2773mm,上偏6.2500mm,探测器单元之间的距离为0.2765mm。
CT系统的起始旋转角度为29.7893°,基本以1°为间隔依次逆时针旋转180°。
2 二维CT图像重建模型
本模型基于傅里叶中心切片定理,用滤波反投影方法建立二维CT图像重建模型。可以根据CT系统的X射线在180个方向上的衰减信息,重构出测量物质的吸收率和几何形状信息。
2.1 滤波反投影重建方法
在CT断层成像技术中,最直接的方法是通过各个方向的扫描信息,直接通过累加法反投影计算出原图像各个像素点的密度(衰减系数)数值。但是由于是在旋转的空间进行重建,所以直接累加会引入星状伪迹,即原图像中密度为零的点,重建后密度不一定为零,图像出现失真。为了克服这种现象,本文在投影以前先对投影数据进行插值和滤波等修正,再把修正后的数据进行反投影得到无伪迹的图像[10-11]。
在利用滤波反投影对CT扫描投影数据进行图像重构时,需要首先选择滤波器的响应函数。通过上面重建原理的分析,可以得到理论上的滤波频率响应函数为ω,但是实际系统存在一定带宽,所以在设计滤波器时一般都有上限频率。传统的方法一般采用Ram-Lak(R-L)滤波器[12],直接对前面的响应函数设计一个带限,如图2(a)所示。但这种滤波器会在高频产生吉布斯现象,使重构的图像边缘产生振荡。因此,这里采用一种更加平滑的方法,Shepp-Logan(S-L)滤波器[13],响应函数的图像如图2(b)所示,可以看作为ω加上了一个光滑约束。
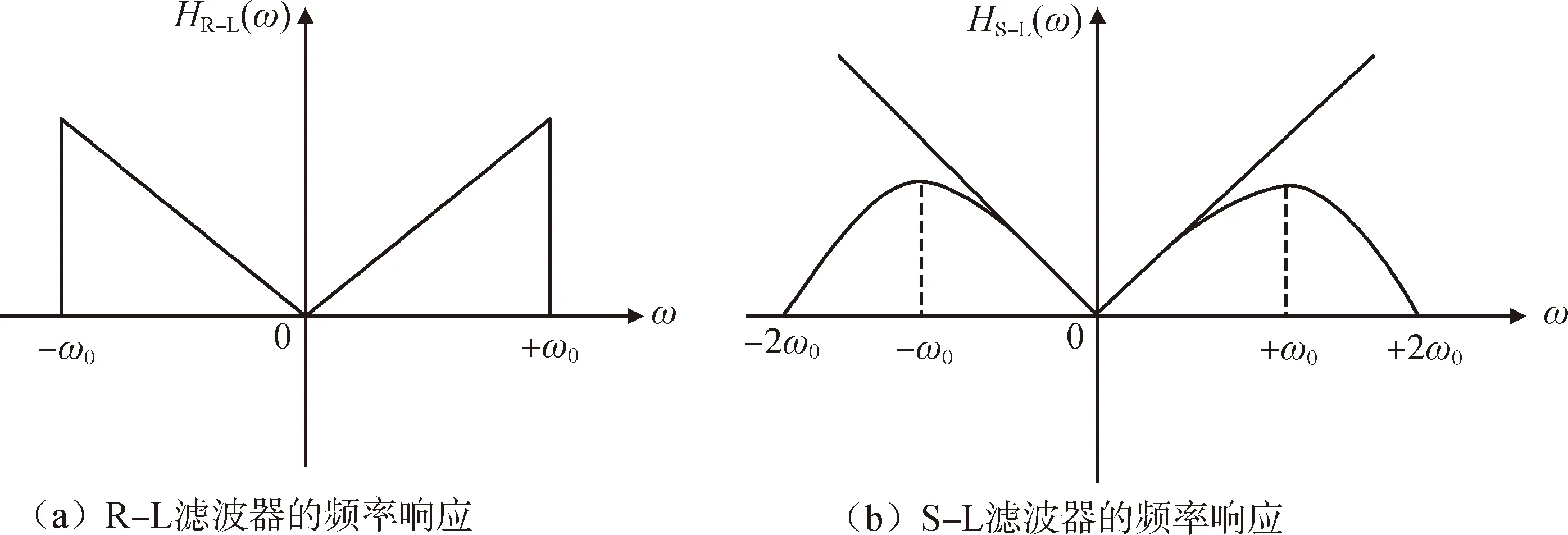
图2 两种滤波器的频率响应
S-L滤波器的窗函数为:
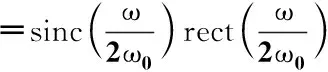
(10)
因此,其频率响应函数为:
对应的卷积函数为:
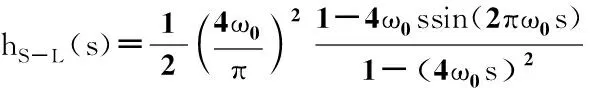
(12)
将180个方向上的投影信息(即X射线的吸收强度)通过滤波器,进行滤波处理,将结果运用反投影方法直接累加得到原图像的吸收率分布,其反投影重建过程如图3所示。
2.2 重建模型求解方法
为了得到探测器接收到的实际衰减信息,需要在滤波反投影重建前对接收信息的增益进行还原。得到衰减信息的数据矩阵:
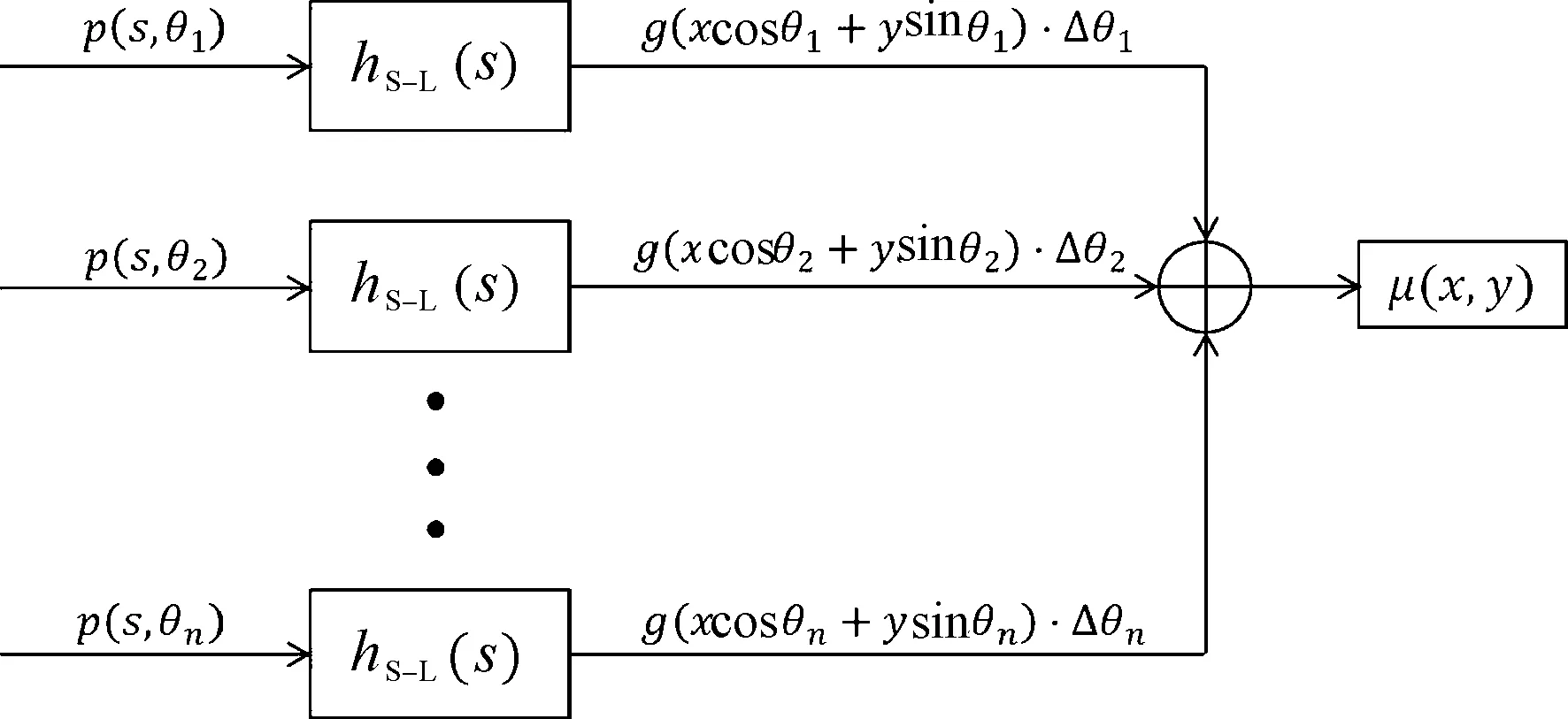
图3 滤波反投影重建过程
(13)
式中,n=512,p=180,λ是CT系统对接收到的衰减信息进行增益的比例,数据矩阵P中的元素pij表示在第j个旋转角度θj下,探测器的第i个单元接收到的衰减信息,pij=p(si,θj)。这个衰减信息等效于该单元的探测直线上吸收率的线积分。
在得到了探测器的实际接收衰减信息后,利用滤波反投影重建方法对原始图像的吸收率分布进行重建。由于旋转中心不一定在重建物体的几何中心,所以在重建前需要在数据矩阵P每一列的首尾增加上100个单位的零填充值,以保证整个图像能被完整还原。
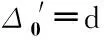
(14)
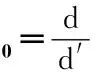
最后,由于滤波反投影重建是一种数值方法,在原图像上吸收率应该为0的地方也会填充有微小数值,所以本文在处理最后结果时,将值小于0.1的点均置0,得到符合真实情况的吸收率分布。
2.3 求解结果
最后得到问题二的吸收率分布情况如图4所示。
同样对问题三进行求解,得到的吸收率分布情况如图5所示。

图4 问题二介质的位置和几何形状

图5 问题三介质的位置和几何形状
2.4 CT图像重建模型的验证
最后,对本文中图像重建的模型和算法进行可行性验证。利用题目附件二的接收信息和已经标定的参数,对模板的位置、几何形状和吸收率进行重建,并与实际结果进行对比,说明了该重建模型和算法的可行性。
图6是利用该CT图像重建算法重构出的模板的位置和几何形状与原始图像的对比。
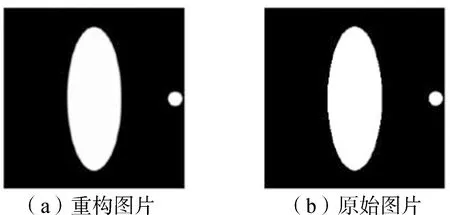
图6 CT图像重建模型的验证
重建结果的位置和几何形状与原图像的符合程度均非常好,只是重构图像在边缘上比原始图像略小一圈,这是因为图像边缘的频率太高,在通过滤波器时会被滤掉,但是这对分析模板的吸收率和确定位置和形状并没太大影响。此外,通过对比重建的模板各点的吸收率差异,可以看到重建吸收率与原始吸收率相比误差极小,验证了该模型的准确性。
3 结束语
对于CT系统参数的标定,本文根据X射线衰减规律得到接受信息的理论计算式,基于最小二乘原理建立了理论与实际接受信息的损失函数,并以未知参数(中心点、探测单元间距、180个旋转角)为决策变量,抓住题目信息隐含的约束条件,建立了单目标优化模型。
由于决策变量过多,采用单目标优化模型直接求解十分困难,甚至得不到正确解。因此按一定规则多次从180组数据中每次抽取6组数据进行分组优化,较好的利用了Radon变换正弦图得到了旋转角的大致初值范围,减小了搜索范围,增大了精度。抽取30次先行计算中心点和单元距离等数据,得到了精确统一的收敛解,然后利用该数据对旋转角变量进行逐组求解,求得了精确的180个CT系统旋转角度值,较好地完成了系统的标定。
对于问题二和问题三CT图像的重建,采取了医学上常用滤波反投影图形重建方法,去除了直接反投影重建算法中会出现的星状伪影,得到了精确的重建图像以及未知介质的具体信息,并利用问题一中的已知模板验证了CT图像重建模型的可行性。

