几何教学中有效培养学生逻辑思维能力的一些思考和做法
上海市建平中学西校 薛肖峰
逻辑思维(Logical thinking),是人们在认识事物的过程中借助于概念、判断、推理等思维形式能动地反映客观现实的理性认识过程,又称抽象思维。它是作为对认知者的思维及其结构以及起作用的规律的分析而产生和发展起来的。只有经过逻辑思维,人们对事物的认识才能达到对具体对象本质规定的把握,进而认识客观世界。它是人的认识的高级阶段,即理性认识阶段。
同时在《上海市中小学数学课程标准》中明确指出,学生需要逐步形成逻辑推理能力,知道进行数学证明的重要性,掌握演绎推理的基本规则和方法;能正确而简明地表述推理过程,合理解释推理的正确性。懂得从数学的角度去思考问题,能有条理地、准确地阐述自己的思想和观点。
这就要求我们初中阶段的数学教师在教学过程中,不仅要重视基本知识和基本技能的教学,更加要注重培养学生们的逻辑思维能力,要引导学生乐于思维,善于思维,即学会如何思维、如何正确地思维、如何更好地思维,从而实现培养学生逻辑思维能力的目标。
下面我来谈谈我在几何教学中,培养学生逻辑思维能力的思考和做法:
一、在概念发生和发展过程中培养学生的逻辑思维能力
初中学生学习几何,是从最基本的几何图形和概念入手,学习一些简单几何图形的性质和判定,从而培养逻辑思维能力。在这个过程中,学生会学到一些新的概念,新的概念的产生,一般也有一个逻辑链。对于这些概念的准确理解,是学生逻辑思维能力形成过程中最基本的环节,我认为只有逻辑关系清楚了,才能进行逻辑思维。为了培养学生发现问题解决问题的能力,提高他们的创新意识,我在平时的教学中特别重视一些基本概念的发生和发展的过程,重视概念和概念之间的关联性、逻辑链,促进学生的理解。举例说明如下:
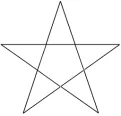
举例1: 在研究直线型图形中,我们往往是从边、角和对角线三个方面展开。在特殊的平行四边形“矩形”的教学设计中,我用几何画板课件动态演示了一个平行四边形是如何转变成一个矩形的过程,由于“边”上没有变化,因此引导学生从“角”和“对角线”这两个不同的角度去观察平行四边形到矩形的变化过程,从而总结出判定一个四边形是矩形的不同的判定方法,让学生知道平行四边形和矩形之间的逻辑关系,以及判定方法。
举例2:对于黄金三角形和比例中项的关系。我们知道,在比例中,如果两个比例内项相等,那么这两个比例内项叫做比例中项。而如果一条线段AB被点P分成长短不一的两段(如AP>PB),其中当AP是AB和PB的比例中项时,那么此时点P是线段AB的黄金分割点。如果一个等腰三角形的底边和腰或腰和底边之比是那么我们把这样的三角形称之为“黄金三角形”,即所谓的“黄金三角形”就是腰长和底边的长之间存在着比例中项的关系。而由五个全等的黄金三角形加上中间一个正五边形,就组成五星红旗中五角星的图案,如图所示。我通过这样的教学设计,更加有助于学生对黄金分割这个概念的理解和掌握,从而能进一步进行逻辑思维。
二、在概念的辨析过程中培养学生的逻辑思维能力
我发现在几何图形中有一些基本概念很容易混淆,所以在这个时候更加需要把这些概念的内涵和外延讲清楚,通过辨析让学生更加准确地掌握各个概念的基本内容,有利于对这些概念的灵活使用。为了达到这个目的,当出现一些和以前学过的概念相类似的概念教学的时候,我会把这些类似的概念放在一起复习讲解,加强学生对于这些基本概念的理解和掌握,正确理解它们之间的逻辑关系,从而培养他们的逻辑思维能力。
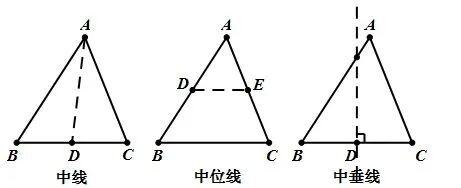
举例3:当学生学到三角形的中位线的这个课时的时候,我会把三角形的中线、三角形边的中垂线和三角形的中位线这三条线的概念进行梳理,让学生分析他们的异同点,加强学生对概念的理解。如图所示:三角形的中线指的是三角形的一个顶点及其对边中点的连线,三角形的中位线指的是三角形两边中点的连线,三角形一边的中垂线仅仅指的是线段的中垂线,且它是一条直线,这些中垂线不一定经过这些边所对的顶点。并且我还会为学生日后的学习埋下伏笔,给他们留几个问题思考,例如①三角形三条中线的交点G到中点的距离和到所对顶点的距离之间的关系;②三角形三条中位线围成的小三角形的周长、面积和原三角形的周长、面积之间的关系;③三角形三条边的中垂线的交点O到三个顶点的距离的关系。这三个问题为学生以后学习三角形的重心定理、相似三角形的性质定理以及三角形的外心做了很好的铺垫。进一步理清有关概念,培养了学生的逻辑思维能力。
三、在几何定理的教学过程中培养学生的逻辑思维能力
学习几何证明,最主要的目的就是培养学生的逻辑思维能力,但这一任务也相当艰巨,因为这对学生来讲是有很大的难度,所以一直是学生学习几何过程中最主要的难点,学生在学习几何证明的过程经常会“所见即所得”,上下文之间没有明确的逻辑关系,或者条件缺失。我发现,这个现象主要是因为学生在学习一些几何定理的时候没有分清楚定理的题设和结论,所以导致书写的时候因果关系不完整,甚至因果关系颠倒。为了尽可能避免这种情况发生,我会在定理教学的过程中,特别注重对于定理的三种不同表达形式的传授,即“文字语言”、“图形语言”和“符号语言”的传授。
举例4:在垂径定理的教学设计中,我不仅要求学生注重这个定理的文字语言表达,即“垂直于弦的直径平分弦并且平分弦所对的两条弧”,着重强调“垂直于弦的直径”是题设,“平分弦并且平分弦所对的两条弧”是结论,尤其是注意题设中实际上包含了两个条件,“直径”和“垂直于弦”,并且配合图形,将符号语言书写格式完整的展示给学生看。

而且,在这个定理及其推论的应用过程中,我也会反复强调必须准备2个条件作为已知的重要性。并且还要特别提醒学生,垂径定理的其中一个推论“平分弦的直径垂直弦并且平分弦所对的弧”当中,这条弦不能是直径,从而体现逻辑推理的严谨性。只有这样严格的要求,学生才能学会正确的逻辑思维方式。
四、在几何证明的训练过程中培养学生的逻辑思维能力
在基础知识落实后,为达到学习几何最主要的目的,我们要学习利用这些基础知识证明一些几何问题,在此时,我特别关注思维解决问题的方式:1.从条件出发,推得结论;2.从结论出发,探寻条件;3.两种方式相结合,获得结论。经常引导学生从这三个方面思考问题,因为这也是我们进行逻辑思维的一般方法。而此时,数学思想的渗透是一个培养学生逻辑思维能力很好的方法。例如:
已知:如图,BE、BF分别是∠ABC与它的邻补角∠ABC的平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F,EF分别交边AB、AC于点M和N.

对于这个问题,根据已知条件,
这一结论,可考虑证明MN是△ABC的中位线,即M、N分别是边AB、AC的中点。这可以由矩形的对角线互相平分证得M是边AB的中点,最后再证MN∥BC,得到N是边AC的中点。而证平行,可考虑把问题转化为证∠MEB=∠EBC,也体现数学的化归思想在培养学生思维能力中的作用。
另外我发现,学生在解决各类几何证明题的过程中不会“触类旁通”,不会“举一反三”,为了更好的培养学生的逻辑思维能力,充分挖掘例题的功能,解决类似的现象,我采取了以下三种策略。
1. 一题多解
在几何教学的过程中,经常会遇到一些问题,它们的解题方法不唯一,学生可以从不同的角度思考和探索,从而得到不同的解题方法。这就需要我们教师经常引导学生梳理解决常见问题的基本方法,那么学生才能会想到解决问题的不同方法,然后通过学生和学生互相交流的方法,促进他们逻辑思维能力的提高。
例如在下述这个问题中要证明两直线平行,我启发学生从不同的维度来思考证明两直线平行的证明方法,培养学生的逻辑思维能力。
方法二:从比例线段的角度上思考,只要证明:

方法三:从三线八角的角度上思考,
可以看到,同样是证明平行,对于不同学段的学生来说,都有各自不同的方法可以证明,体现了几何证明中“一题多解”的特点。如果学生能够把这几种方法分析清楚,那么对于学生来说,以后再碰到证明两直线平行的问题,他们就可以从不同的角度去思考了。对于提高学生的逻辑思维能力来说,起到了非常重要的拓展思维的作用。
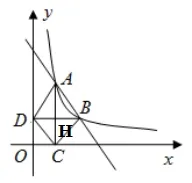
方法四:利用面积证明,即只要证明△ABD和△ABC的面积相等,我们就比较容易证得CD∥AB。
2. 多题一解
在有些问题中,虽然题目的已知条件不同、图形也不同,但是解决这些问题的方法确实一致的。学生只要通过归纳总结,就可以得到一个行之有效的方法来解决这一类问题,达到“举一反三”的效果,进一步提高自己的逻辑思维能力。
例如:以下这一组问题,就可以采取相同的方法来解决。
举例6:如图,在△ABC与△DEF中,∠A=∠D,AB=6,AC=5,DE=4,若△ABC与△DEF相似,求DF的长。
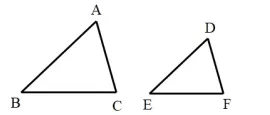
解法分析:由于∠A和∠D的两边对应关系不确定,所以有两种对应关系,分别是:或者再将已知条件代入得到两个方程:分别解方程即可。
举例7:如图,在△ABC中,点D是边AC上的中点,其中AB=9,AC=6,问边AB上是否存在点E,使得△ADE与△ABC相似。
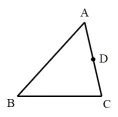
解法分析:由于∠A是这两个三角形的公共角,而△ADE中AD的对应边不确定,
举例8:如图,在梯形ABCD中,AD//BC,AD⊥AB,点E为线段AB上不与A、B重合的点,且AD=2,BC=3,AB=7,当△ADE与△EBC相似时,求出AE的长及DE∶EC的值
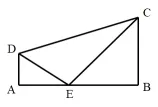
解法分析:图中∠A=∠B=90°,而这两个角的两边的对应关系不确定,所以有两种对应关系,分别是:或者再将已知条件代入得到两个方程:或分别解方程即可。
举例9:如图,在平面直角坐标系中,点A(1,0),点C(2,1),点D在直线x=1上,当△AOC与△ADC相似时,求点D的坐标。
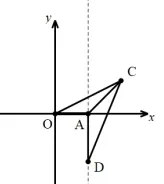
解法分析:经过分析发现,点D只能在直线x=1中位于x轴下方的部分上,此时∠OAC=∠CDA=135°,那么这两个角的边的对应关系就有两种可能再将线段AO、AC的长度分别代入得:分别解方程可得或 1 则点D坐标为(1,-2)或(1,-1)
可以看到,在这些不同问题的背后,实际上隐藏着相同方式的解法。虽然题目的图形和条件略有不同,解题要求也略有不同,但是分析问题的方法和思维的角度基本是一直的。学生只要掌握了正确的思维方法,就可以准确的解决这一类问题。
3.一题多变
有些问题及其图形
例如在相似三角形的判定和性质的教学过程中,我做了如下的教学设计来培养学生的逻辑思维能力:
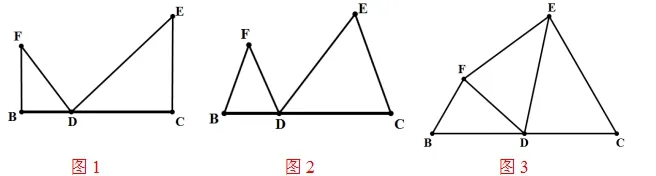
这个过程,体现了从特殊到一般,再从一般到特殊的变化,在这个变化过程中,有不变的关系,也有改变的内容。学生可以从中体会到几何图形变化中的奥妙,对于提高学生的逻辑思维能力起到积极的作用。
总之,学生从入门的几何概念几何图形几何定理开始不断地学习,一直到较复杂的逻辑推理论证,这是一个个漫长的过程。在这个漫长的过程中,老师要严谨治学、一丝不苟地给学生做好示范,还要给学生创造自主的学习环境,激发学生的创新意识,既要“脚踏实地”也要“异想天开”,要求学生遵守逻辑规则,正确运用各种定理和方法。只有这样,才能完成培养和提高学生的逻辑思维能力的任务。

