三次三角域Bézier曲面的同次扩展

严兰兰，温荣生，饶智勇



三次三角域Bézier曲面的同次扩展

严兰兰，温荣生，饶智勇

(东华理工大学理学院，江西 南昌 330013)

为了在不提升基函数次数的前提下赋予三次三角域Bézier曲面形状调整的能力，构造了一组含一个参数的三次双变量基函数，由之定义了由10个控制顶点确定的三角域曲面片。新曲面具有角点插值性，在角点处的切平面为由角点和其所在的两条边上与之相邻的两个顶点确定的平面。改变参数取值，可以调整曲面形状。为了方便应用，给出了曲面片之间的1光滑拼接条件及曲面的几何迭代算法，分析了算法的收敛性以及收敛速度与参数取值之间的关系。图例显示了所给方法的正确性和有效性。

三角域Bézier曲面；形状调整；几何迭代；插值；曲面拼接

在几何设计中，Bézier方法是应用较为广泛的曲线曲面表示方法之一，其包括Bézier曲线、四边域上的张量积Bézier曲面、三角域上的Bernstein- Bézier曲面。虽然Bézier方法具有很多利于形状设计的优良性质，但也存在不足。当控制顶点给定时，Bézier曲线曲面的形状便被唯一确定，若要调整形状，只能修改控制顶点，重新计算曲线曲面方程。这种方式不仅使用不便，而且当控制顶点是取自实物的精确测量点时，修改控制顶点显得有些勉强。

与曲面相比，曲线结构相对简单，更易于讨论，目前有很多文献通过在基函数中引入参数，来赋予Bézier曲线形状调整的能力。由于张量积Bézier曲面与Bézier曲线均以单变量Bernstein多项式作为基函数，因此只要构造出能对Bézier曲线作改进的基函数，就可以对张量积Bézier曲面作出相应改进。然而Bernstein-Bézier曲面为非张量积形式，其采用双变量Bernstein多项式作为基函数，要想对三角域Bézier曲面作改进，必须单独为其构造基函数。

三角域曲面具有重要的应用价值，其可以避免矩形域曲面片出现退化的问题，适合于不规则与散乱数据点的几何造型，因此研究带形状参数的三角域曲面片的构造方法是有意义的。目前围绕三角域Bézier曲面在形状调整方面的不足进行改进的成果主要有：文献[1]和[2]分别构造了含3个、6个参数的三次双变量多项式基函数，定义了以二次三角域Bézier曲面为特例的曲面；文献[3]构造了含3个参数的三次双变量多项式基函数，文献[4]和[5]分别构造了含1个、2个参数的四次双变量多项式基函数，文献[3-5]中的曲面都以三次三角域Bézier曲面为特例；文献[6]和[7]分别构造了含1个、多个参数的次双变量多项式基函数，定义了以任意次三角域Bézier曲面为特例的曲面；文献[8]构造了+1次双变量多项式基函数，定义了以任意次三角域Bézier曲面为特例的含多个形状参数的曲面；文献[9]在初始三次双变量多项式基函数的基础上递推得到+1次基函数，文献[10]和[11]在初始四次双变量多项式基函数的基础上递推得到+2次基函数，文献[9-11]中的曲面都含1个形状参数，并以任意次三角域Bézier曲面为特例；文献[12-14]定义了结构与三次三角域Bézier曲面相同的含3个形状参数的曲面，文献[12]和[13]定义在三角多项式空间中，文献[14]定义在指数函数和多项式函数的混合空间中。

上述文献均从纯代数角度出发，直接给出含参数的调配函数来定义新曲面，且少有文献讨论曲面的光滑拼接条件和几何迭代算法，这不利于曲面的应用。本文则基于由可调控制顶点定义可调曲面的直观几何思想，通过在控制顶点中引入参数，构造含1个形状参数的三次三角域Bézier曲面，讨论了曲面的1光滑拼接条件，给出了曲面的几何迭代算法及收敛性分性，为曲面的应用提供了理论基础，也为构造其他类型的形状可调曲线曲面提供了可以借鉴的思路和方法。

1 形状可调曲面

1.1 曲面构造原理

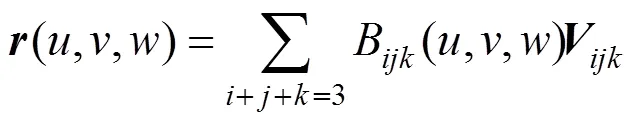
曲面(,,)具有轮换对称性、凸包性、角点插值性；曲面的边界曲线为由边界控制顶点定义的三次Bézier曲线；曲面在角点处的切平面为由角点和其所在的两条边上与之相邻的控制顶点张成的平面。

将*(,,)看作普通三次三角域Bézier曲面，即

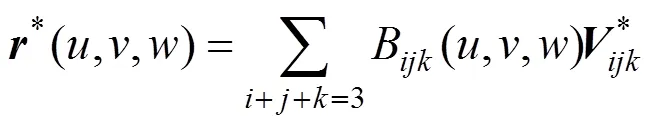
则其控制顶点为

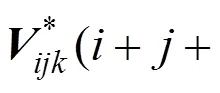
1.2 调配函数及性质

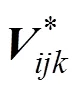
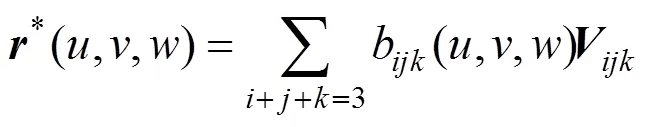
其中，b(,,) (简记为b)的表达式如下

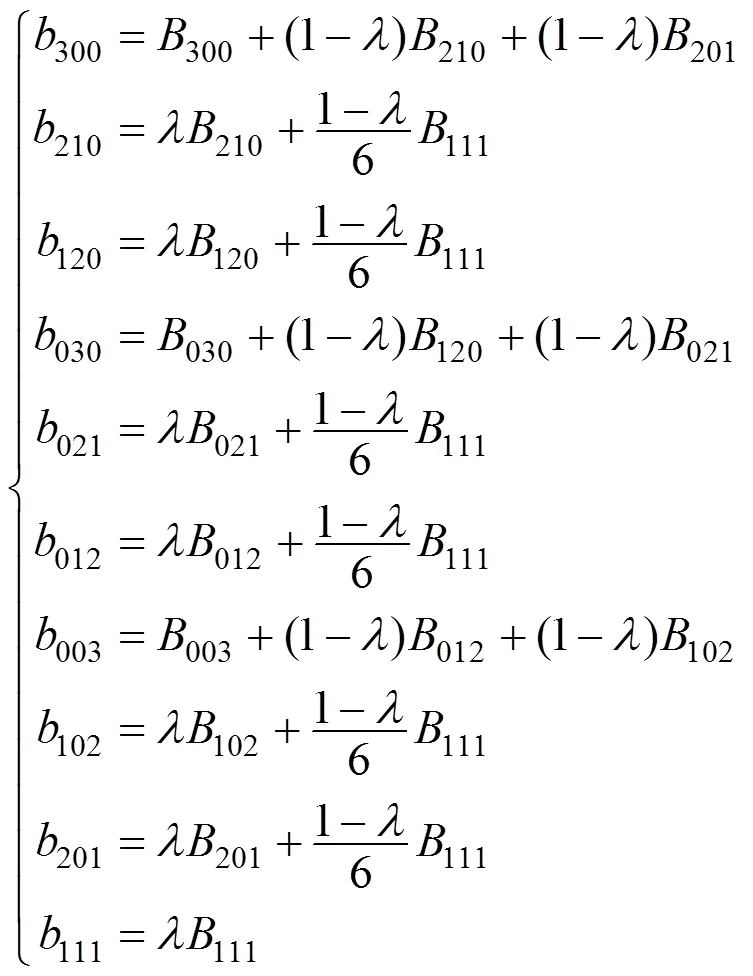
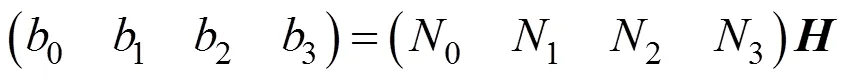
其中

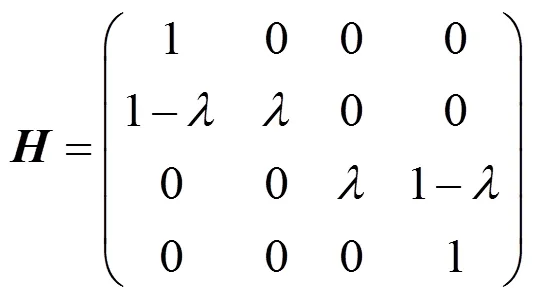
由式(4)及双变量三次Bernstein基函数的性质，可得双变量函数的性质如下：

(1) 退化性。当=1时，双变量函数为双变量三次Bernstein基函数。

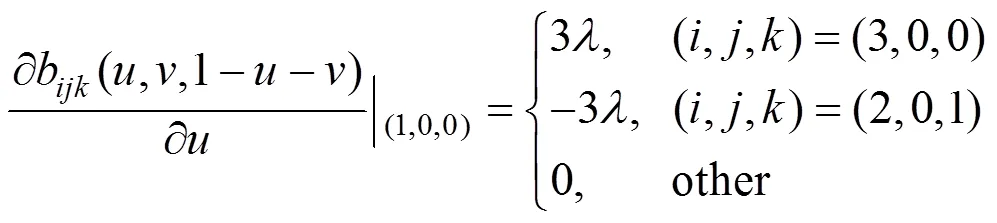
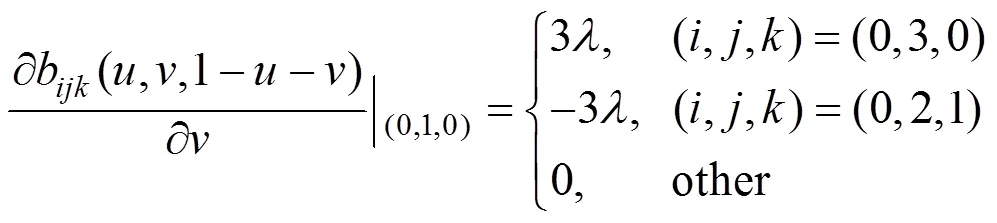
证明：设

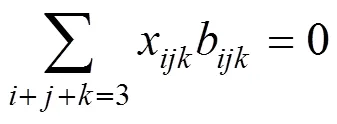
由双变量三次Bernstein基函数的线性无关性得

1.3 曲面性质

由调配函数的性质，可知三角-Bézier曲面具备下列性质：

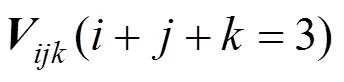
(3) 角点插值性。曲面插值于控制网格的3个角点，即

(4) 角点切平面。曲面在角点(1,0,0)处的切平面由点300、210和201张成；在角点(0,1,0)处的切平面由点030、120和021张成；在角点(0,0,1)处的切平面由点003、012和102张成。

图1 取不同参数的三角l-Bézier曲面

2 曲面拼接

为了满足描述复杂形状的需求，下面讨论三角-Bézier曲面的光滑拼接条件。

2.1 三次三角域Bézier曲面的拼接

设有两张三次三角域Bézier曲面

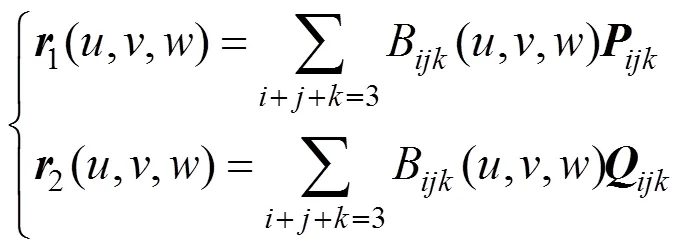
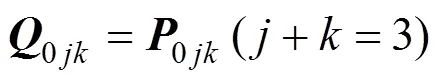
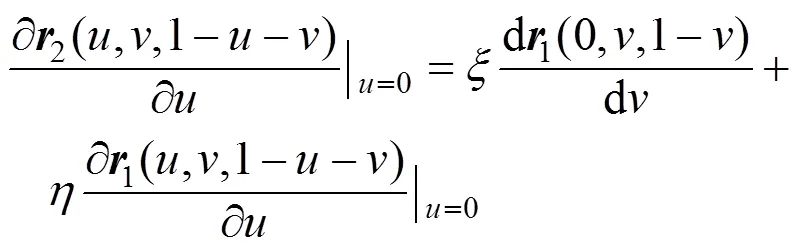
其中，、为任意因子。条件式(9)可转化为

式(8)、(10)即为三次三角域Bézier曲面的1光滑拼接条件。

2.2 三角l-Bézier曲面的拼接

设有两张三角-Bézier曲面

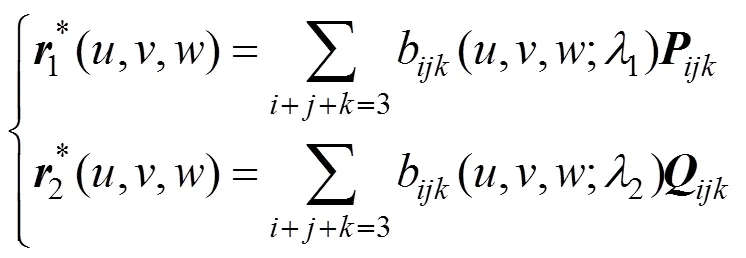
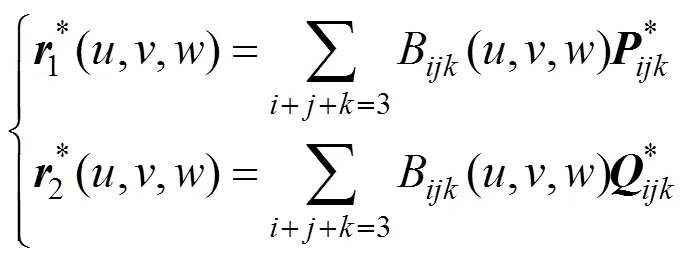
由式(8)可知，当

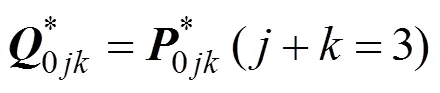
进一步地，由式(10)可知，若

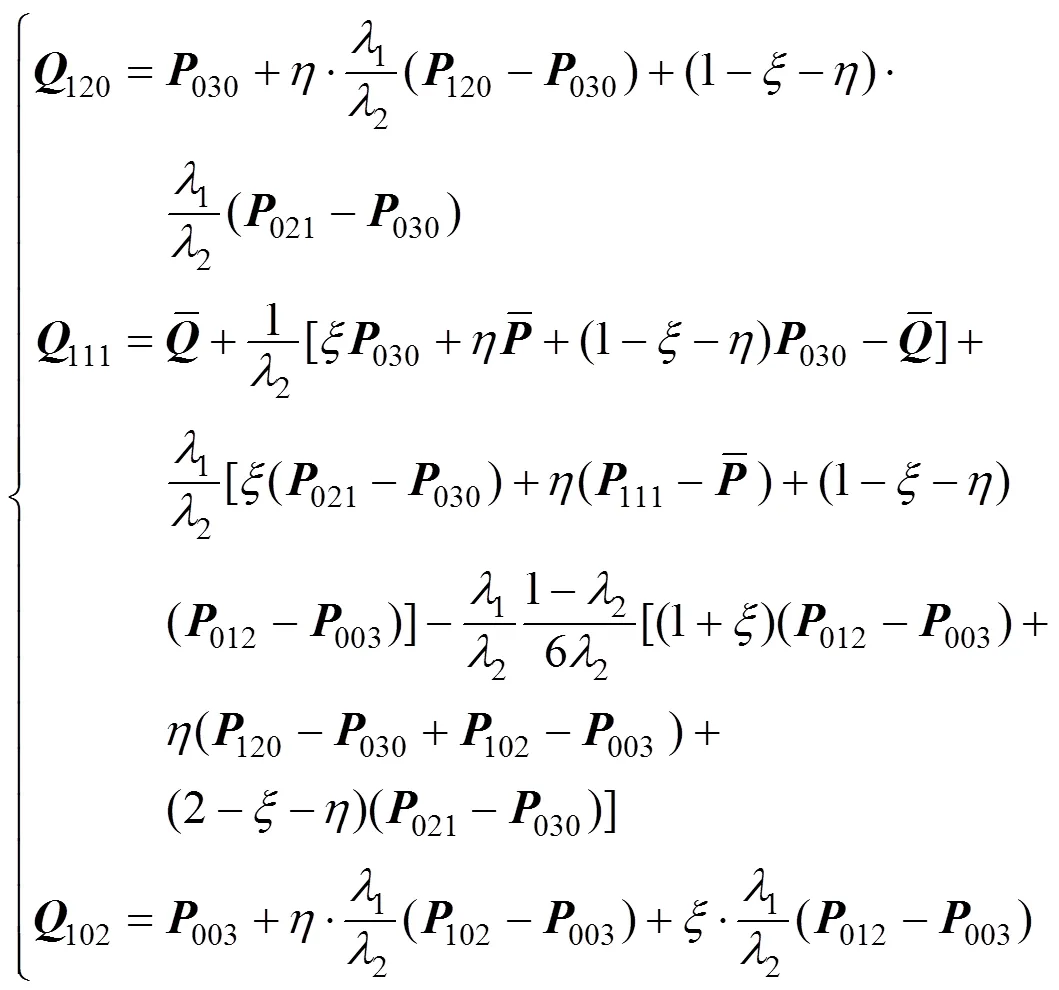
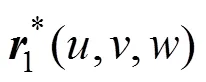
3 曲面的几何迭代算法

几何迭代法[15]具有明确的几何意义。该方法从一条初始曲线或一张初始曲面开始，通过迭代调整其控制顶点，使曲线曲面插值或逼近给定点列。

3.1 算法描述

(c)

构造第+1次迭代曲面

3.2 收敛性分析

即曲面序列收敛到插值初始点列的曲面，则称三角-Bézier曲面对均匀参数具有渐进迭代逼近性质。

将赋给控制顶点的参数也按字典排序法排列，即

由式(17)可得

其中，为10阶单位矩阵；为调配函数(18)关于参数序列式(19)的配置矩阵，即

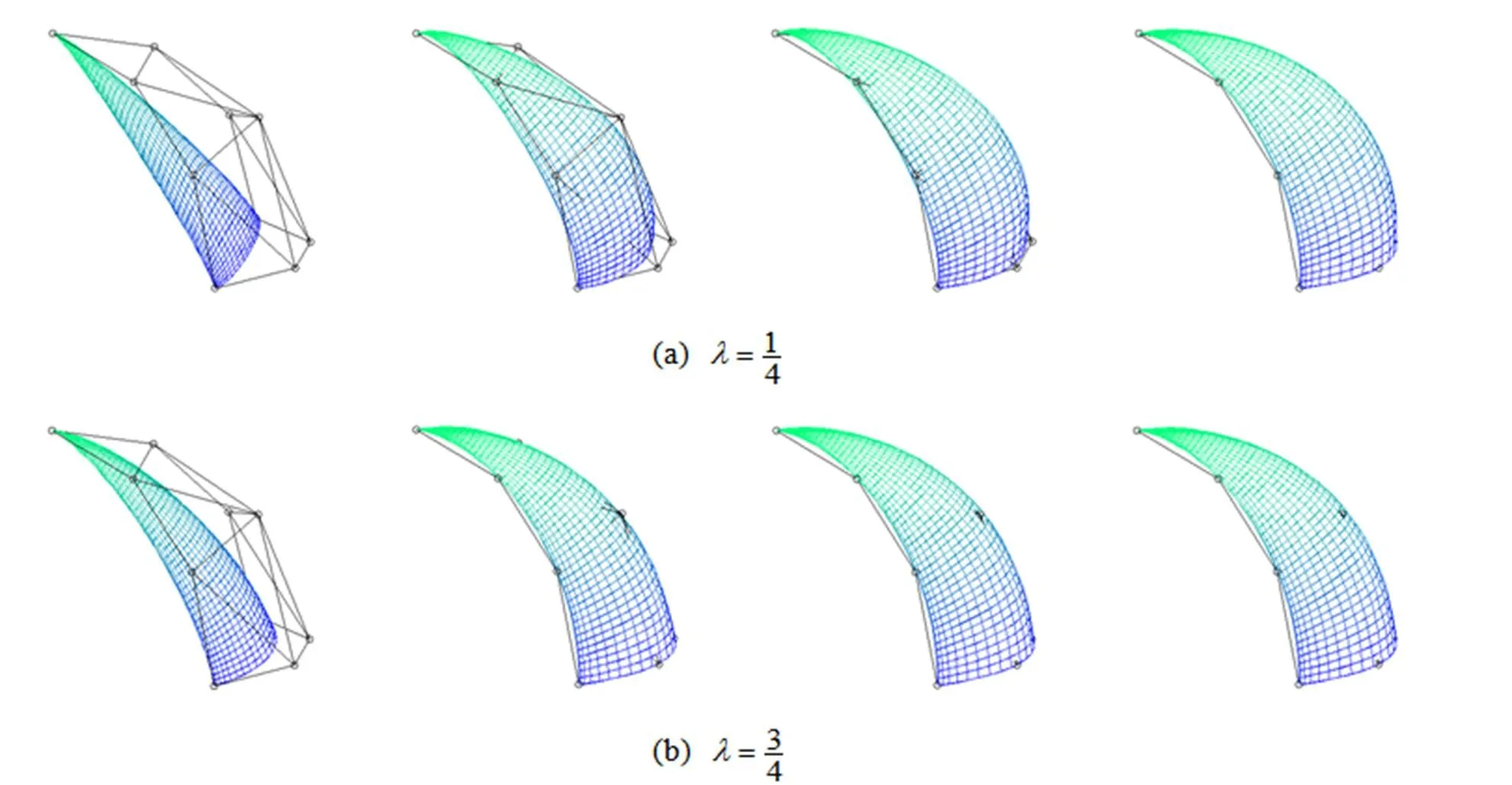
图3 迭代所得三角l-Bézier曲面

4 结束语

本文从纯几何角度出发对三次三角域Bézier曲面从形状表示的灵活性角度进行扩展，通过在控制顶点中引入参数，再与双变量Bernstein基函数作线性组合来定义曲面，当参数改变时，定义曲面的潜在控制顶点发生改变，曲面形状随之变化。在赋予曲面形状可调性时，本文既未改变基函数的函数类型，也未提升基函数的多项式次数。为降低曲面拼接条件的分析难度，先给出传统三次三角域Bézier曲面的拼接条件，再通过形状可调曲面与三次三角域Bézier曲面之间的关系，给出了新曲面的1光滑拼接条件。为构造视觉上插值于控制顶点的三角域曲面，讨论了曲面的几何迭代算法，对其收敛性、收敛速度进行了分析，为曲面应用提供了理论基础。

[1] 陈军. 一类带三个形状参数的三角曲面[J]. 计算机集成制造系统, 2013, 19(11): 2680-2685.

[2] 韩西安, 黄希利. 三角域上带多个形状参数的二次Bézier曲面片[J]. 装甲兵工程学院学报, 2011, 25(1): 99-102.

[3] 刘植, 檀结庆, 陈晓彦. 三角域上带形状参数的三次Bézier曲面[J]. 计算机研究与发展, 2012, 49(1): 152-157.

[4] 曹娟, 汪国昭. 三角域上三次Bernstein-Bézier参数曲面的扩展[J]. 计算机辅助设计与图形学学报, 2006, 18(9): 1403-1407.

[5] 于立萍. 三角域上带两个形状参数的Bézier曲面的扩展[J]. 大学数学, 2008, 24(5): 58-62.

[6] CAO J, WANG G Z. An extension of Bernstein-Bézier surface over the triangular domain[J]. Progress in Natural Science, 2007, 17(3): 352-357.

[7] ZHU Y P, HAN X L. Quasi-Bernstein-Bézier polynomials over triangular domain with multiple shape parameters[J]. Applied Mathematics and Computation, 2015, 250: 181-192.

[8] 邬弘毅, 夏成林. 带多个形状参数的Bézier曲线与曲面的扩展[J]. 计算机辅助设计与图形学学报, 2005, 17(12): 2607-2612.

[9] 吴晓勤, 韩旭里. 带有形状参数的Bézier三角曲面片[J]. 计算机辅助设计与图形学学报, 2006, 18(11): 1735-1740.

[10] YAN L L, LIANG J F. An extension of the Bézier model[J]. Applied Mathematics and Computation, 2011, 218(6): 2863-2879.

[11] 严兰兰. 带形状参数的Bernstein-Bézier曲面[J]. 计算机工程与科学, 2014, 36(2): 317-324.

[12] ZHU Y P, HAN X L. New trigonometric basis possessing exponential shape parameters[J]. Journal of Computational Mathematics, 2015, 33(6): 642-684.

[13] HAN X L, ZHU Y P. A practical method for generating trigonometric polynomial surfaces over triangular domains [J]. Mediterranean Journal of Mathematics, 2016, 13(2): 841-855.

[14] ZHU Y P, HAN X L. Curves and surfaces construction based on new basis with exponential functions[J]. Acta Applicandae Mathematicae, 2014, 129(1): 183-203.

[15] 蔺宏伟. 几何迭代法及其应用综述[J]. 计算机辅助设计与图形学学报, 2015, 27(4): 582-589.

[16] CHEN J, WANG G J. Progressive iterative approximation for triangular Bézier surfaces[J]. Computer-Aided Design, 2011, 43(8): 889-895.

Extension of the Cubic Triangular Bézier Surface of the Same Degree

YAN Lanlan, WEN Rongsheng, RAO Zhiyong

(College of Science, East China University of Technology, Nanchang Jiangxi 330013, China)

In order to endow the cubic triangular Bézier surface the ability of shape adjustment, this paper constructs a set of cubic bivariate basis functions with a parameter and defines a new triangular surface determined by ten control points. The new surface has corner interpolation property. The tangent planes at the corner points are determined by the corner points and the two adjacent points which lie on the same edges. Changing the parameter value can adjust the shape of the surface. For convenient application, the1smooth join condition and the geometric iterative algorithm of the surface are given. The convergence as well as the relationship of the convergent rate and the parameter selection of the algorithm is analyzed. The legends show the correctness and validity of the method.

triangular Bézier patch; shape adjustment; geometric iteration; interpolation; surface joining

TP 391.72

10.11996/JG.j.2095-302X.2018010097

A

2095-302X(2018)01-0097-07

2017-05-18；

2017-06-20

国家自然科学基金项目(11261003，11761008)；江西省自然科学基金项目(20161BAB211028)；江西省教育厅科技项目(GJJ160558)

严兰兰(1982–)，女，湖北浠水人，副教授，博士。主要研究方向为计算机辅助几何设计。E-mail：yxh821011@aliyun.com