标准测试系统中PSS参数协同优化与配置研究
陈子文
(国网湖南省电力有限公司永州供电分公司,湖南 永州 425000)
0 引言
电力系统稳定器(power system stabilizer, PSS)通常用于增强系统阻尼、抑制低频振荡,其参数常由试验整定[1-2]。随着最优化方法的发展,群智能优化算法被引入到PSS参数优化设计中[3-5]。有的还设计、开发了集PSS参数计算与仿真校核于一体的、具有人机交互界面的PSS参数计算综合软件,将理论计算PSS参数设定到励磁调节器上[6-7]。
文献[8]提出基于广域测量信号的PSS设计,用基于混沌和差分进化的混合粒子群算法对PSS和直流调制控制器参数进行协调优化,在EPRI 36节点系统仿真验证协调策略的正确性与有效性。文献[9]改进模拟植物生长优化算法(PGSA),在4机2区系统算例中仿真,研究附加阻尼控制器和PSS之间的协调优化策略,用特征根分析和时域仿真结果证明改进PGSA能有效阻尼低频振荡并增强系统的小干扰稳定性。文献[10]用相位补偿法和粒子群算法对宽频段PSS模型参数进行优化,通过实时数字仿真(real time digital simulator, RTDS)和现场实测,说明优化的PSS4B能够满足不同宽频段的要求,抑制低频振荡。文献[11]建立大规模风机并网后的系统线性化模型,用粒子群算法求最优解,协调整定双馈风机附加阻尼控制器和PSS控制参数,通过2个仿真算例,对比验证其PSS设计策略。文献[12]设计兼顾机电和非机电振荡模式的目标函数,用粒子群算法求解,以3机系统为算例,优化设计双馈风机附加阻尼控制环节与PSS参数,用时域仿真验明阻尼特性。文献[13]简化PSS4B传递函数,保留带通滤波环节,用粒子群算法优化整定PSS参数,基于算例验证低频振荡抑制效果。文献[14]将PSS4B待优化参数分为两部分,用粒子群算法,分2次相位补偿协调优化,在单机无穷大系统中仿真验证。文献[15]用留数指标筛选机组,改进粒子群算法,在云南电网3个小水电群中应用,协调优化PSS参数,提高小水电群的整体送出能力。文献[16]提出自适应加速粒子群算法(SAPSO),对某电网B厂2台机PSS参数进行协调预整定,并对预整定参数和现场实测参数的阻尼效果进行时域仿真与现场试验对比,为现场整定提供依据。
关于PSS参数协调优化及设计的研究中,多数针对几台机组的测试算例,仅应用算法进行PSS参数优化研究,有关PSS安装地点配置选择及PSS配置及参数合理性校核研究甚少,系统性研究更少。
文献[17]考虑PSS输入和输出信号馈入两方面影响,提出了PSS配置的综合参与因子法,仅在4机2区系统中配置,经验证比传统的参与因子配置法更有效。文献[18]提出基于特征值对PSS传递函数的灵敏度以及阻尼比对PSS放大倍数的灵敏度分析方法,进行PSS的配置以及放大倍数的整定,仅在4机2区系统验证。
文中首先对IEEE-57测试系统的振荡模式和阻尼特性分析,校核已投PSS装置及其参数的合理性。然后运用SAPSO算法,对单台机组PSS参数进行单机优化,依据参数因子大小,合理配置系统PSS安装地点,并协同优化与振荡模式相关的PSS参数,系统性地研究了第15、18号发电机组(简称15、18号机)在不同情形下获得的PSS参数对测试系统阻尼比的影响。最后利用小干扰稳定时域仿真和普罗尼算法(prony algorithm,别称Prony分析),验证协同优化的PSS参数阻尼效果,验证PSS参数协同优化配置的方法切实可行。
1 IEEE-57测试系统阻尼特性分析
1.1 IEEE-57测试系统概述
IEEE-57测试系统包含33台发电机,57个母线节点,32条线路(2条双回线路,30条单回线),35台双绕组变压器。该系统结构及规模都能够满足分析计算的要求,算例系统节点数目适宜,机电振荡模式及阻尼特性明显,在进行多机系统中PSS参数的协同优化及配置,以抑制互联系统的低频振荡的研究中,首选IEEE-57测试系统作为算例进行分析,其优化及配置效果、步骤更清晰。
1.2 测试系统振荡模式与阻尼特性分析
假定IEEE-57测试系统运行在大负荷方式,对系统做特征值和特性向量的小干扰稳定分析,并按照“参与因子在1~0.002之间、阻尼比小于0.03、振荡频率在0.1~2.5之间”3条原则对系统低频振荡模式进行筛选,得出系统负阻尼或弱阻尼低频振荡模式。其中阻尼比小于0.03的机电振荡模式仅有1个,该模态的振荡频率为1.146 7 Hz,阻尼比为0.017 9,属于弱阻尼振荡模式。
分析与该弱阻尼振荡模式相关机组的参与因子,发现较高的7台相关机组为18、17、15、9、4、5、10号机。18号机的参与因子最高为1.00;其次为17号机,参与因子为0.99;18、17号机均未装PSS。在这些参与因子较高的机组中,仅15号机安装了PSS,其参与因子为0.77,其他机组参与因子依次为0.62,0.6,0.6,0.46。
在不改变电网结构,不另增其他PSS装置的前提下,抑制该弱阻尼振荡模式的办法是对15号机的PSS参数进行优化。但为进一步研究15号机对该弱阻尼振荡模式的影响,分析该振荡模式的机理,宜先分析15号机PSS装置投退前后的小干扰稳定,以校核其抑制振荡的效果。
1.3 第15号机PSS投退校核分析
现退出15号机组PSS,对系统进行小干扰稳定分析,阻尼比小于0.03的机电振荡模式仅有1个,其振荡频率为1.14 Hz,阻尼比为0.017 6,也是弱阻尼振荡模式。进一步分析该弱阻尼振荡模式的参与因子,发现与该模式相关的机组有15、18、17、9、4、5、10号等机组。与该机电振荡模最相关的仍是15号机,其次为17、18号机。
15号机组PSS退出运行后,系统存在阻尼比为0.017 6的振荡模式,而该振荡模式与第15机相关因子最大,即在15号机上安装PSS是正确的。但是15号机PSS投入运行后,系统所有振荡模式中最小的阻尼比只有0.017 9,仅仅提高了0.000 3,振荡频率分别为1.146 7 Hz和1.14 Hz,也很相近,且又都与15、18、17号机强相关(参与因子分别达0.77和0.98以上,明显高于其他机),说明这是同一个机电振荡模式。
以上分析表明,15号机的PSS投运,对系统的弱阻尼振荡提高不明显,没能有效抑制该机电模式的低频振荡,因此15号机的PSS参数设计不合理,故对其进行优化。
2 IEEE-57系统中PSS参数优化配置
2.1 15号机PSS参数优化
15号机PSS模型为PSS2A型,其参数为测试系统依据其励磁系统结构和参数,对照PSS2A模型各参数的推荐值选取配置,与相位补偿相关的增益和时间常数的主要PSS参数如表1所示。其中:Tw1为PSS隔直环节时间常数1;KS1为PSS增益;T1和T3为相位补偿环节的超前时间常数;T2和T4为相位补偿环节的滞后时间常数。
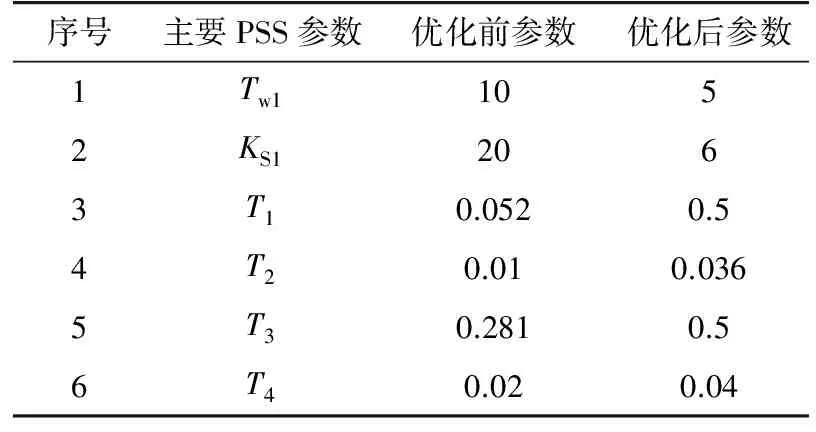
表1 15号机的主要PSS参数Tab.1 Main PSS parameters of No.15 generator
利用SAPSO算法[16]对15号机PSS参数进行优化配置,以达到有效提高测试系统的阻尼比,抑制振荡的目的。SAPSO算法数学模型中粒子更新迭代速度方程如式(1)所示,位置方程如式(2)所示。
V(t+1)=ωV(t)+C1R1[Xp(t)-X(t)]+C2R2[Xg(t)-X(t)]
(1)
X(t+1)=X(t)+V(t)
(2)
式中:t为迭代序数;V是粒子速度矩阵;X是粒子位置矩阵;Xp为每个粒子前t次迭代内找到的个体最优位置矩阵;Xg为粒子群前t次迭代内找到的最优位置矩阵;ω为惯性权重;C1和C2为加速因子;R1和R2为[0,1]之间的随机数矩阵。
算法协同优化PSS参数的目标函数为式(3)。
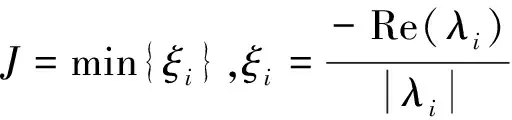
(3)
式中:λi为特征值;i为机电模式序数;ξi为第i个机电振荡模式阻尼比;Re为取复数实部的函数。
算法终止条件为N次迭代结束或满足误差精度,优化过程中的目标函数(即系统机电振荡模式的最小阻尼比最大)的动态变化过程如图1所示。优化前后的PSS参数对比如表1所示。
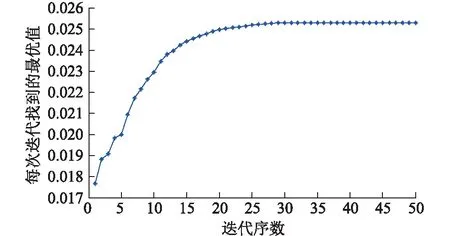
图1 优化过程中系统机电振荡模式的最小阻尼比变化Fig.1 The minimum damping ratio variation of oscillation model in the optimization process
将15号机的PSS输入经过优化的参数后,进行小干扰稳定分析,阻尼值小于0.03的机电振荡模式仍有1个,其特征值为-0.282 2+j7.208 3,振荡频率为1.147 2 Hz,阻尼比为0.025 3,小于0.03,仍然是一个弱阻尼振荡模式,与该弱阻尼振荡模式相关机中参与因子最高的为18号机,其次为17号机。
仅通过优化15号机的PSS参数,就可以将系统的阻尼比由之前的0.017 9提高到了0.025 3,优化效果还是十分明显的。但系统阻尼比仍小于0.03,进一步分析该机电振荡模式的模态图可知,该振荡模式是一个区间振荡模式,因此仅优化15号发电机的PSS参数,并不能完全提高区间振荡模式的阻尼比。故考虑在参与因子较大的18号机上配置PSS以提高该区间振荡模式的阻尼比,满足系统对阻尼比的要求。
2.2 18号机PSS配置及参数优化
15、18号机的励磁系统结构参数基本相同,故18号机的PSS模型可选择与15号机同型的PSS2A型。同理2.1节,对18号机进行PSS配置设计,并进行优化,获得主要PSS参数。其中隔直时间常数Tw1为10;增益KS1为6;超前时间常数T1和T3为0.5;滞后时间常数T2和T4为0.036。
在15、18号机上分别配置各机单独优化出的PSS参数,再对测试系统进行低频振荡模式与阻尼特性分析,发现系统已不存在阻尼比小于0.03的振荡模式,计算得到阻尼比小于0.05的振荡模式共有5个,如表2所示。
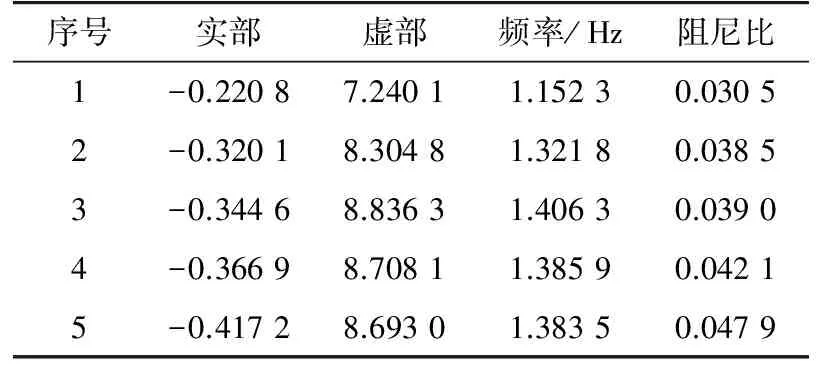
表2 15和18号机单独优化后阻尼比小于0.05的机电振荡模式Tab.2 The oscillation mode with dampingratio less than 0.05 of No. 15 and 18 generatorafter single optimization
通过配置并优化18号机的PSS参数,系统阻尼比能够提高到0.03以上,对阻尼比为0.030 5的机电模式进行参与因子分析,证明它正是之前所研究的区间振荡模式,该弱阻尼振荡模式的阻尼比已经由之前的0.025 3提高到了0.030 5。
2.3 测试系统两机PSS参数协同优化
多机电力系统中存在多个机电振荡模态,各机电振荡模式之间存在着阻尼的耦合。每台PSS的作用都将影响到所有的振荡模态,单个PSS对一个振荡模态有较强的抑制作用,同时它也有可能对另一个模态的振荡起助增作用。即为抑制某一机电振荡模式,进行PSS参数优化,增大其阻尼,则可能会降低恶化另一个机电振荡模式的阻尼。因此在多机系统中进行PSS参数优化时,为避免产生“弱阻尼漂移”现象,需要进行多机系统PSS参数的协同优化,以达到满意的效果[16]。
上述2.1与2.2节对测试系统15、18号2台发电机PSS参数都是分别进行单独优化的,并未考虑两机PSS参数优化时的相互影响,因而考虑对15、18号机进行协同优化。重新调整SAPSO算法,对15、18号机PSS参数进行协同优化后,获得两机参数如表3所示。
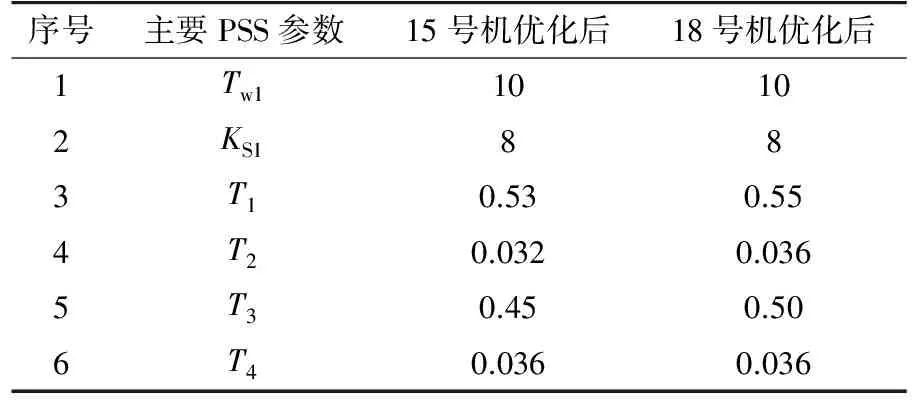
表3 多机协同优化后的第15和18号机PSS参数Tab.3 Main PSS parameters of No.15 and No.18generator after coordinated optimization
将15、18号机PSS参数整定为经协同优化后的PSS参数,对测试系统进行低频振荡模式与阻尼特性分析,测试系统不存在阻尼比小于0.03的负阻尼或弱阻尼低频振荡模式,计算得到的阻尼比小于0.05的振荡模式共有5个,如表4所示。
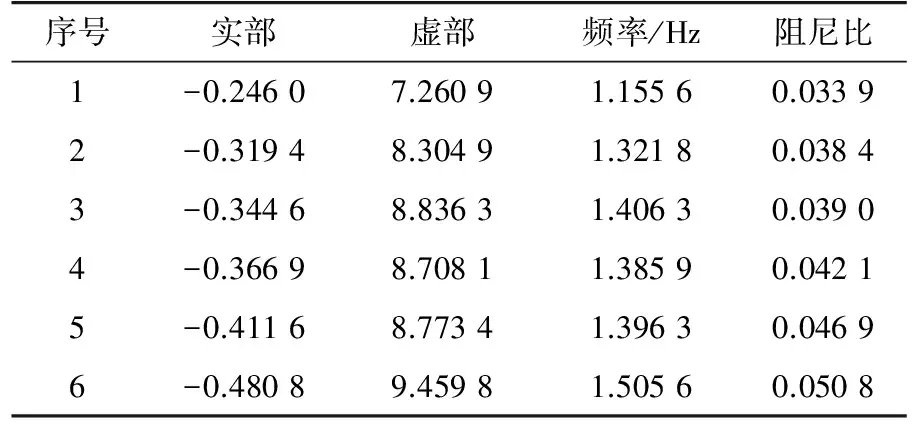
表4 15和18号机协同优化后阻尼比小于0.05的机电振荡模式Tab.4 The oscillation mode with damping ratioless than 0.05 of No.15 and No.18 generator aftercoordinated optimization
对15和18号机的PSS参数进行多机协同优化后,测试系统阻尼值均已达0.033 9及以上,优化出来的PSS参数要优于单独优化15和18号机时的参数(相应阻尼比为0.030 5)。进一步分析特征值为-0.246+j7.260 9的参与因子,发现与之最相关的机组与1.2节相似,证明此机电振荡模式与1.2节相同,阻尼确实升高。因此,在已有的PSS装置基础上只需要对PSS的参数进行协同优化就能够进一步提高系统的阻尼比,无需再增加其他PSS设备,避免在所有机安装PSS装置的盲目性,经济效益明显。
3 小干扰稳定时域仿真分析
3.1 小扰动稳定性时域仿真分析
为进一步验证测试系统15、18号机PSS参数在各自进行独立优化和协同优化的前后,提高系统阻尼水平的效果,对测试系统15、18号机的PSS参数分别在以下这3种情形的运行状态下建立仿真案例,进行5%励磁电压阶跃的小干扰稳定时域仿真分析,观察其动态响应过程。
(1) 未对15号机PSS参数进行优化;
(2) 15、18号机取单机优化PSS参数;
(3) 15、18号机取协同优化PSS参数。
在t=1 s时,在15号机上加5%的励磁电压阶跃扰动,得到15号机有功出力曲线如图2所示。同理,得到18号机有功出力曲线如图3所示。
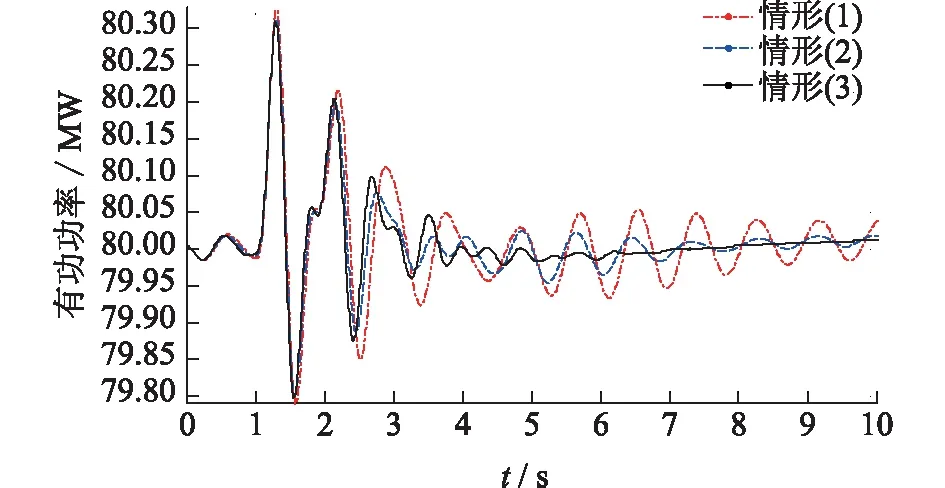
图2 15号机有功功率振荡曲线Fig. 2 Active power oscillation curves of No.15 generator
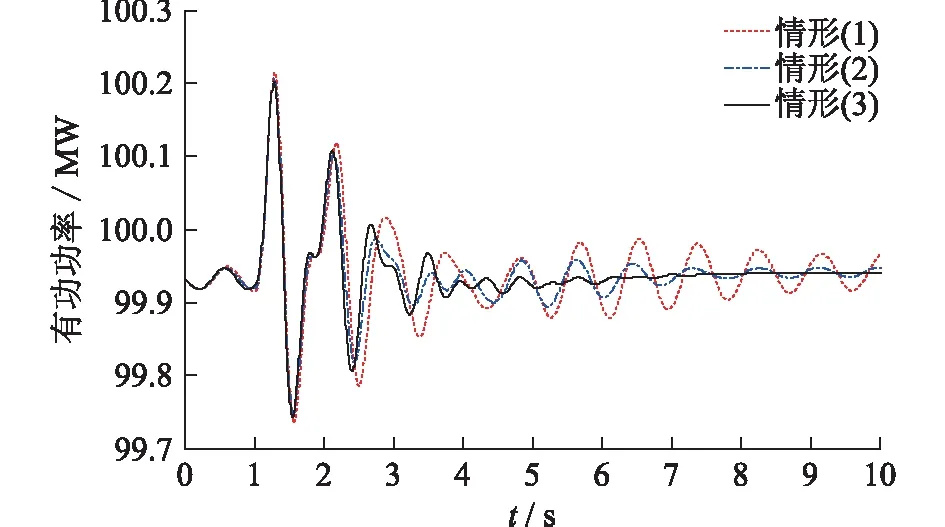
图3 18号机有功功率振荡曲线Fig. 3 Active power oscillation curves of No.18 generator
对比观察图2的15号机有功功率出力曲线,可以看到15号机配置未优化参数时,其动态响应曲线是明显的弱阻尼振荡;在15、18号机配置各自独立优化出来的PSS参数时,有功响应曲线是明显衰减的,阻尼得到了加强。而给15、18号机配置协同优化后的PSS参数时,有功响应振荡曲线很快就衰减平息了。说明协同优化后的PSS参数对应的小干扰动态响应曲线要优于独立优化各单台发电机PSS参数时的有功响应曲线。
3.2 对有功出力曲线进行 Prony 分析
对时域仿真的有功出力曲线做Prony分析,得出时域仿真的机电振荡阻尼特性结果与进行小干扰稳定分析的结果一致,如表5所示。
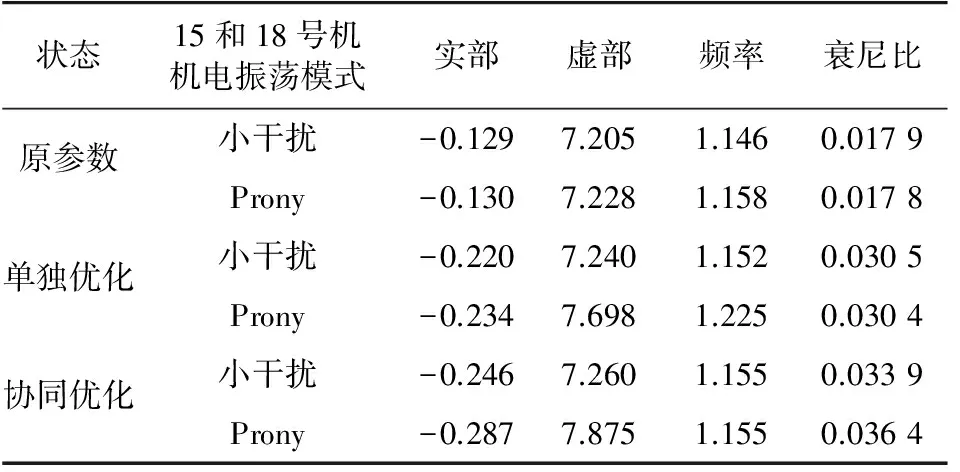
表5 振荡模式及阻尼特性分析结果对比Tab.5 Result comparison of oscillation mode anddamping characteristics analysis
测试系统在情形(1)的运行状态下,用Prony算法分析15号机加5%励磁电压扰动时对应的有功响应曲线,得出低频振荡模式特征值为-0.13+j7.278,阻尼比为0.017 89,振荡频率为1.158,而进行小干扰稳定分析时对应振荡频率为1.146 7 Hz,阻尼比为0.017 9。2种方法获得系统低频振荡的模式和该模式对应的阻尼特性是一致的。
同理,测试系统分别在情形(2)、(3)的状态下,用Prony算法分析15号机加5%励磁电压扰动时的有功响应曲线,2种分析方法所获得的系统低频振荡模式及阻尼特性也一致。
4 结论
为研究协同优化及配置电力系统PSS装置参数是否切实可行,文中选取IEEE-57节点测试系统作为一个算例,先分析测试系统的振荡模式和阻尼特性,校核已投PSS抑制低频振荡的效果。再运用SAPSO算法逐步优化分析,对比测试系统的振荡模式和阻尼水平,探究15、18号机在不同情形下获得的PSS参数对测试系统阻尼比的影响,为在实际电力系统中设计和配置PSS及其参数,提供切实可行的方法。利用小干扰稳定分析、时域仿真分析及Prony分析结果,可以验证在对IEEE-57节点测试系统进行PSS参数优化配置时,文中方法可行,其在多机系统中对PSS参数进行协同优化的效果明显,能有效增加系统的阻尼比,提高整个系统动态稳定水平。在已有PSS装置基础上只需要对PSS的参数进行协同优化就能进一步提高系统的阻尼比,无需增加其他PSS设备。
[1] 赵晓伟,谢 欢,吕思昕,等. 电力系统稳定器PSS4B的参数整定及现场试验[J]. 电网技术,2016,40(2): 508-513.
ZHAO Xiaowei,XIE Huan,LU Sixin,et al. Parameter setting and on-site test of power system stabilizer -PSS4B[J]. Power System Technology,2016,40(2):508-513.
[2] 刘喜泉,毕欣颖,陈小明,等. 770 MW水轮发电机组PSS2B试验与参数整定[J]. 大电机技术,2016(2):37-41.
LIU Xiquan,BI Xinying,CHEN Xiaoming,et al. Test and parameter-setting of power system stabilizer-PSS2B of 770 MW hydro-generator units[J]. Large Electric Machine and Hydraulic Turbine,2016(2):37-41.
[3] PANDA S,YEGIREDDY N,MOHAPATRA S.Hybrid BFOA-PSO approach for coordinated design of PSS and SSSC-based controller considering time delays[J]. International journal of electrical power and energy systems,2013,49(7):199-202.
[4] SUI X,TANG Y,HE H,et al. Energy-storage-based low-frequency oscillation damping control using particle swarm optimization and heuristic dynamic programming[J]. IEEE Transactions on Power Systems, 2014,29(5):2539-2548.
[5] 林子杰,刘建坤,陈 静,等. 基于粒子群算法的MMC-UPFC参数优化[J]. 江苏电机工程,2015,34(6),23-26.
LIN Zijie,LIU Jiankun,CHEN Jing,et al. A PSO algorithm based approach for optimizing MMC-UPFC control system parameters[J]. Jiangsu Electrical Engineering,2015,34(6):23-26.
[6] 徐俊华,李啸骢,裴云庆,等. PSS参数计算与仿真综合软件的设计与开发[J]. 中国电力,2017,50(2):162-168.
XU Junhua,LI Xiaocong,PEI Yunqing,et al. Design and development of PSS parameters calculation and simulation software[J]. Electric Power,2017,50(2):162-168.
[7] 刘玉方,徐 珂. 电力系统稳定器PSS2B参数整定软件的开发与应用[J]. 电气应用,2017,36(8):16-20.
LIU Yufang,XU Ke. Development and application of PSS2B parameter setting software[J]. Electrotechnical Application,2017,36(8): 16-20.
[8] 王 曦,李兴源,赵 睿. 基于相对增益和改进粒子群算法的PSS与直流调制协调策略[J]. 中国电机工程学报,2014,(34):6177-6184.
WANG Xi,LI Xingyuan,ZHAO Rui. Coordination strategy of PSS and DCM based on relative gain and improved PSO [J]. Proceedings of the CSEE,2014,(34):6177-6184.
[9] 付红军,潘励哲,林 涛,等. 基于改进模拟植物生长算法的PSS与直流调制的协调优化[J]. 电力自动化设备,2013,33(11).75-80.
FU Hongjun,PAN Lizhe,LIN Tao,et al. Coordinative optimization of PSS and DC-modulation based on improved PGSA[J]. Electric Power Automation Equipment,2013,33(11):75-80.
[10] 沈 鑫,马红升,李仕林,等. 基于相位补偿法和粒子群算法的PSS4B参数优化方法[J]. 电子器件,2016,39(5):1244-1250.
SHEN Xin,MA Hongsheng,LI Shilin,et al. A method of PSS4B parameters optimization based on the phase compensation method and particle swarm algorithm [J]. Chinese Journal of Electron Devices,2016,39(5): 1244-1250.
[11] 张 辰,柯德平,孙元章. 双馈风电机组附加阻尼控制器与同步发电机PSS协调设计[J]. 电力系统自动化,2017,41(8): 30-37.
ZHANG Chen, KE Deping,SUN Yuanzhang. Coordinative design for supplementary damping controller of doubly-fed induction generator and PSS of synchronous generator[J]. Automation of Electric Power Systems,2017,41(8):30-37.
[12] 郑 华,李 忠,陈 凡. 双馈风机附加阻尼控制环节与PSS的参数协调优化[J]. 江苏电机工程,2015,34(3): 25-29.
ZHENG Hua,LI Zhong,CHEN Fan. Study on parameter coordination and optimization of DFIG auxiliary damping controlling unit and PSS[J]. Jiangsu Electrical Engineering,2015,34(3):25-29.
[13] 刘英超,王德林,康积涛,等. 新型电力系统稳定器PSS4B参数优化整定方法[J]. 电工技术,2017,(5):16-18.
LIU Yingchao,WANG Delin,KANG Jitao,et al. A parameter optimization and setting method of new power system stabilizer-PSS4B [J]. Electric Engineering,2017,(5):16-18.
[14] 朱良合,李文意,毛承雄,等. 新型电力系统稳定器模型分析及参数协调优化[J]. 水电能源科学,2014,32(6):171-175.
ZHU Lianghe,LI Wenyi,MAO Chengxiong,et al. Model analysis and parameter coordination optimization of new PSS [J]. Water Resources and Power,2014,32(6): 171-175.
[15] 刘 蔚,赵 勇,吴 琛,等. 一种提高多小水电群送出能力的PSS参数协调优化方法[J]. 电力系统保护与控制,2015,(4):44-50.
LIU Yu,ZHAO Yong,WU Chen,et al. A method of PSS parameters coordinated optimization for the improvement of transmission capacities of multiple small hydropower station groups[J]. Power System Protection and Control,2015,(4):44-50.
[16] 万 源,段志远,陈子文,等. 基于SAPSO算法的新投PSS参数协调预整定[J]. 现代电力,2014,31(4): 60-65.
WAN Yuan,DUAN Zhiyuan,CHEN Ziwen,et al. Parameter coordinated pre-tune of new operational PSS based on SAPSO[J]. Modern Electric Power,2014,31(4):60-65.
[17] 吴复霞,王金健,潘家骏,等. 电力系统稳定器的配置方法[J]. 中国电力,2016,49(9):13-17.
WU Fuxia,WANG Jinjian,PAN Jiajun,et al. Determination of suitable locations for power system stabilizers[J]. Electric Power,2016,49(9): 13-17.
[18] 徐千茹,崔 勇. 基于特征值灵敏度的电力系统稳定器配置及参数整定[J]. 华东电力,2014,42(10): 2069-2073.
XU Qianru,CUI Yong. Allocation and parameter tuning of PSS based on eigenvalue sensitivity[J]. East China Electric Power,2014,42(10):2069-2073.

