考虑决策风险的含UPFC多目标最优潮流计算
李 斌, 刘建坤, 李 群,杨 光, 卫志农, 何天雨, 张清松
(1. 国网南京供电公司,江苏 南京 210019; 2. 国网江苏省电力有限公司电力科学研究院,江苏 南京 211103; 3. 河海大学能源与电气学院,江苏 南京 211100; 4. 国网江苏省电力有限公司检修分公司,江苏 南京 211102)
0 引言
风电是具有可再生性的绿色清洁能源,但同时存在随机性、间歇性等缺点,随着其在电网中的渗透率日益提高,有可能导致电压越限、潮流越限等问题,对电力系统的安全稳定构成威胁[1-4]。而统一潮流控制器(unified power flow controller, UPFC)作为目前通用性最好的柔性交流输电(flexible AC transmission system, FACTS)装置,具有多种控制功能,能快速、灵活地调整电网参数,为电网调度提供新的手段[5-6]。目前,我国第一套UPFC也是世界上第一套基于模块化多电平的UPFC示范工程于2015年12月11日在江苏南京西环网顺利投运[7-8]。2016年11月3日,全球电压等级最高、容量最大的江苏苏州南部电网示范工程正式开工建设,计划2017年底建成投运。因此,文中考虑利用UPFC来协调风电的不确定性。
在含有风电的系统中,风电出力发生波动时,实际发电总成本同期望的成本会产生较大偏差,将这种偏差情况作为决策风险性。期望成本的偏差意味着发电机组出力的偏差,而由于风电的波动,极有可能发生不同场景间机组调节能力不足的情况。因此,为了降低潜在的决策风险性,有必要考虑决策风险对优化运行带来的影响。基于上述分析,建立考虑决策风险的含UPFC的多目标最优潮流模型,通过算例分析验证文中所提模型的准确性。
1 UPFC稳态模型
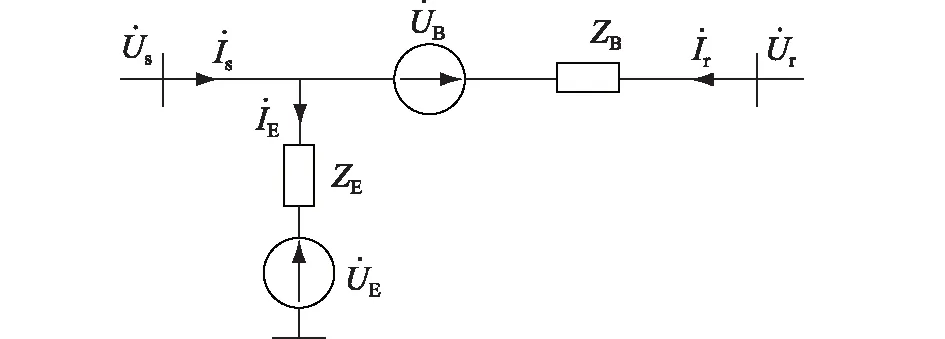
图1 UPFC的双电压源模型Fig.1 Dual voltage source model of UPFC
在具体计算过程中,可将UPFC对系统的影响等效为对其所在支路两端节点的注入功率Psr+jQsr,Prs+jQrs,等效示意图如图2所示,等效注入功率可用式(1)表示:
(1)
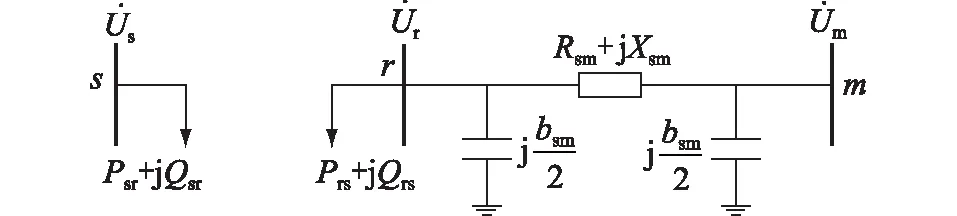
图2 UPFC支路等效示意图Fig.2 Equivalent schematic diagram of UPFC branch
2 考虑决策风险含UPFC多目标最优潮流
投资组合理论中称投资结果对期望收益的偏差为投资风险,借鉴该概念,将优化调度带来的成本偏差称为决策风险。常用的最小化期望成本的模型由于没有考虑风电不确定性因素的影响,并不能体现隐藏的决策风险,当遇到风电不确定性影响较大即偏差较大的场景时可能会使电网蒙受重大损失。在投资理论中,衡量风险最常用的模型是均值-方差模型,即用方差刻画决策的风险性[10-11],文中参考投资理论采用期望-方差的目标函数来衡量决策风险。
2.1 模型
(1) 目标函数。考虑决策风险性的最优潮流应当权衡优化的期望值和方差,因此该模型中目标函数有2个。首先设定每个场景每个时段的发电费用为:
(2)
式中:PGi[s,t]为场景s下机组i在时段t的有功出力;a2i,a1i,a0i为第i台发电机发电费用系数;ng为系统发电机数。
那么,目标函数一为多场景多时段下的平均发电费用,即发电机发电费用的期望值,表达式如下:
(3)
式中:S为描述场景的集合;T为描述时段的集合;ps为描述场景概率的集合;nTime为时段数量,一般为24个时段。
目标函数二为多场景多时段下的发电费用方差,表达式如下:
f2(x)=
(4)
(2) 等式约束。考虑决策风险性的多目标最优潮流模型的等式约束和不等式约束同常规最优潮流约束条件类似,但由于文中所建立模型是建立在多场景以及多时段的基础上,因此对于每个场景每个时段约束条件都应该能够满足要求。
等式约束包含节点功率平衡方程和UPFC内部有功功率平衡方程。其中,普通节点的功率平衡方程在此不作详述。UPFC所在线路两端节点的功率平衡方程和UPFC内部有功平衡方程如式(5—6)所示。
(5)
PE[s,t]+PB[s,t]=0
(6)
式中:i取s或r,j的取值集合为{1,2,3,...,n};[s,t]中的场景s∈S,时段t∈T。
(3) 不等式约束。不等式约束包括发电机约束、节点电压约束、线路潮流约束及UPFC运行约束。
(7)
(8)
式中:UE,max,UE,min,UB,max,UB,min分别为UPFC并联、串联电压源幅值上、下限;θE,max,θE,min,θB,max,θB,min分别为UPFC并联、串联电压源相角上、下限。
2.2 基于法线边界交叉法的求解方法
多目标问题在一开始是通过权重法求解,主要思想是将其转化为一个单目标问题,再利用数学规划进行求解,由于每次只能设定一个权值,所以每次只能得到一种权值情况下对于该问题的最优解。另外,由于目标函数的单位普遍不同以及约束通常非线性、不可微等一系列限制,对于选取的权重值也较敏感。
另一种求解多目标问题的思路是找寻到一系列的帕累托(Pareto)最优解,决策者只需根据需要从Pareto前沿上选择出合适的解。在多个目标函数间权衡折衷的过程就可以用这个选择的过程来代表。这个方法相较于普通设定权重的方法具有较高的实用性,在各个领域的优化问题方面得到普遍应用。
一般求解多目标问题的方法包括约束法,智能算法(遗传算法、粒子群算法等)以及法线边界交叉法(normal boundary intersection, NBI)。除NBI法以外的算法不仅可能无法得到均匀分布的Pareto前沿,还可能致使最优解集不够准确,而采用法线边界交叉法可以得到准确且均匀的Pareto前沿[12-13]。
根据前文所述,选用法线边界交叉法进行多目标的求解,具体步骤介绍如下。
首先写出如下形式的确定性多目标优化模型:
(9)
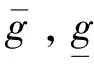
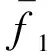
(10)
式中:fij表示当以第i个目标函数做单目标优化时第j个目标函数的解。
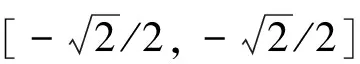
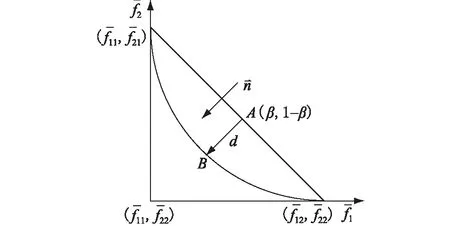
图3 规范化乌托邦直线与Pareto前沿Fig.3 Normalized Utopia line and Pareto front
(11)
式中:参数β是乌托邦直线上任意一点A的横坐标,可以将区域[0,1]平均划分为20份或者10份来确定β的值。那么该多目标问题便可以转化为一系列目标函数为d的单目标优化问题。
2.3 算法流程
利用原对偶内点法求解上述转换后的单目标优化模型,具体流程如图4所示。
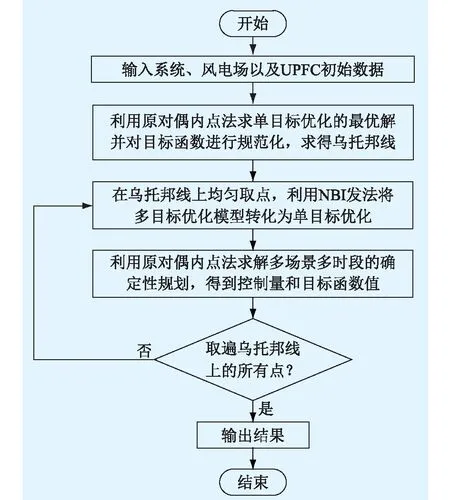
图4 基于NBI的多目标优化流程Fig.4 Multi objective optimization flow chart based on NBI
3 算例分析
3.1 测试算例说明
针对文中所提模型及求解方法,对IEEE-14节点系统进行修改。UPFC安装于线路4—5的节点4侧,风电接在节点9,新增节点15。系统拓扑如图5所示。
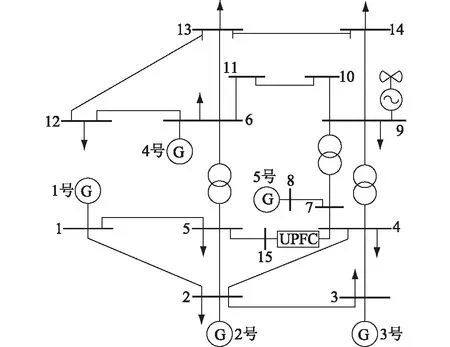
图5 加装UPFC和风电后的IEEE-14系统拓扑Fig.5 Topological diagram of IEEE-14 system after installing UPFC and wind power
以文献[14]中的历史数据作为风速预测值进行计算分析,选取ALGONA地区2010年7月4日24 h整点的风速数据作为预测值,并以整点的风速代表这1 h的风速,详细数据见附表。同样假定某一整点的风速服从以预测值为期望,以预测值的5%为标准差的正态分布。对每个期望值采用文献[15]中介绍的基于概率距离最短的场景削减方法得到Ns组场景,文中取Ns为5。
假定风电场额定功率Pr=80 MW,切入风速vin=3 m/s,额定风速vr=12 m/s,切出风速vout=25 m/s。附表中S1~S5为削减得到对应5个场景下的各时段风电场出力。
3.2 算法性能测试
以修改后含有风电场和UPFC的IEEE-14节点系统为例,为表明多目标优化的协调决策性能,构造3种优化方案进行比较分析。
方案1:以发电费用最小作为单目标的优化;
方案2:以发电费用方差最小作为单目标优化;
方案3:以发电费用及其方差最小作为多目标的优化。
方案3中,双目标优化利用NBI法进行多目标求解,选取Pareto曲线上11组最优解,如表1所示。进而画出该多目标问题的Pareto前沿,如图6所示。其中Pareto前沿的两个端点分别为以发电费用最小和发电费用方差最小作为单目标的优化结果。
通过观察图6能够发现,法线边界交叉法能够得到准确且均匀分布的Pareto前沿,即作出的Pareto前沿上的每个点都是一个最优解。在实际的系统运行调度中,操作人员可以依据实际的需要选择Pareto前沿对应的最优解来确定多目标优化下的运行方案。
为保证选择决策方案的客观性,参考文献[16]中提到的熵权法来确定最优解集中的最优决策方案,进而再将选择的多目标最优方案作为方案3同方案1和方案2下的结果进行比较。最终所得3种方案下的优化结果如表2所示。
表1 多目标优化Pareto曲线数据
Tab. 1 Multi objective optimization of Pareto curve data
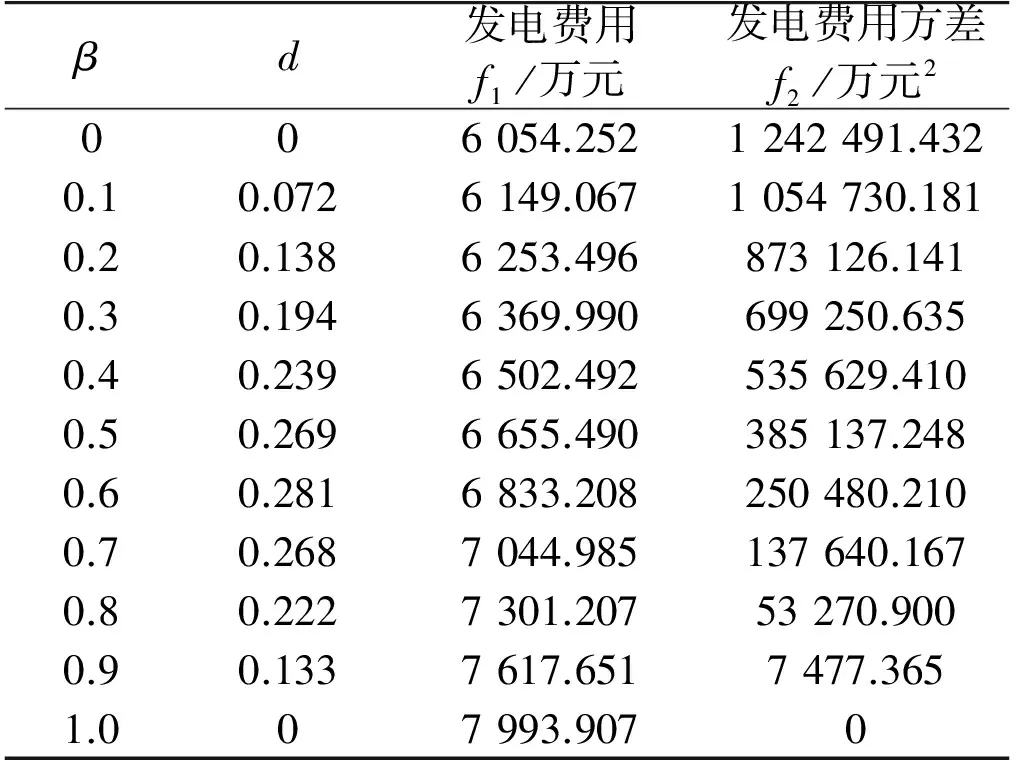
βd发电费用f1/万元发电费用方差f2/万元2006054.2521242491.4320.10.0726149.0671054730.1810.20.1386253.496873126.1410.30.1946369.990699250.6350.40.2396502.492535629.4100.50.2696655.490385137.2480.60.2816833.208250480.2100.70.2687044.985137640.1670.80.2227301.20753270.9000.90.1337617.6517477.3651.007993.9070
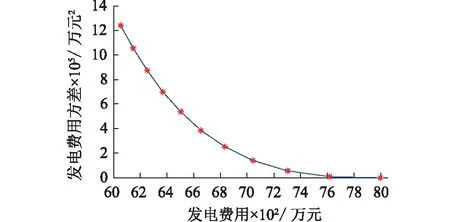
图6 多目标问题的Pareto前沿Fig.6 Pareto front of multi objective problem
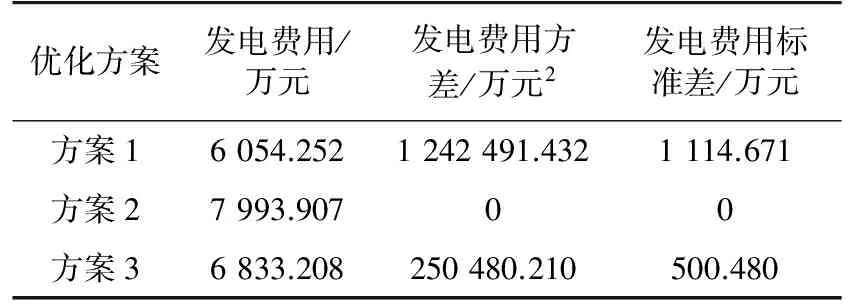
表2 3种方案的优化结果Tab. 2 Optimization results of three schemes
从表2中可以看出,方案1单纯考虑节省发电费用,会导致不同场景不同时段间的发电费用方差较大,增大了机组调整出力的风险性;而方案2仅考虑降低各场景各时段下的发电费用方差,甚至能够达到方差为0,减少了机组调节的风险性但却使得系统的发电费用增加;方案3为多目标协调决策的结果,该方案综合考虑了发电费用最小和发电费用的方差最小,所得决策在每个场景每个时段均是较好的,更具有现实意义。
为进一步验证所建立的多目标模型考虑决策风险性的能力,分别对3种方案下各场景各时段的发电机出力以及UPFC的控制参数进行算例测试。图7为IEEE-14节点测试系统中发电机2的出力示意图。
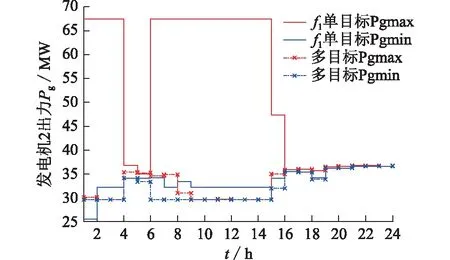
图7 IEEE-14节点系统发电机2的出力示意图Fig.7 Schematic diagram of output power of generator 2 in IEEE-14 node system
图7中,沿场景来看,多目标优化时各场景下的最大最小出力较单目标来说更加紧凑,表明多目标的最优解虽然对于各个风电场景来说不是最优解但均为接近最优的解,发电机出力在某时段的不同场景间均无需做过多的调节;沿时段来看,单目标优化时各个时段发电机2的出力变化较大,而多目标优化时发电机2的出力能够保持在比较平稳的范围内,这表明加上方差最小作为目标函数优化后,能够使各时段发电机出力的调节更加平稳,减少了发电机来不及调整的风险。
最后对多目标优化下UPFC串联等效电压源的幅值UB在不同场景不同时段的取值进行分析研究,如图8所示。可以看到在对应风速波动性较小的时段1—3、时段8—14以及时段19—24,UPFC串联等效电压源的幅值在各个场景下没有较大改变,但是在风速波动性较大的时段4—7、时段15以及时段18,UPFC串联等效电压源的幅值UB的调节范围有所扩大。
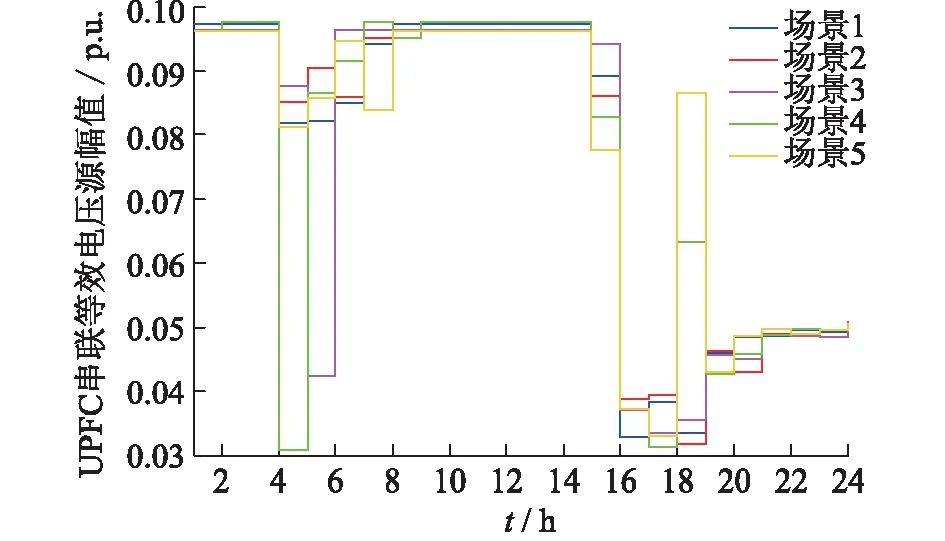
图8 多目标优化下UB在不同场景及时段的取值Fig.8 The value of multi objective optimization in different scenarios and periods
在上述风速波动较大的时段下UB调节的最大、最小值如表3所示。
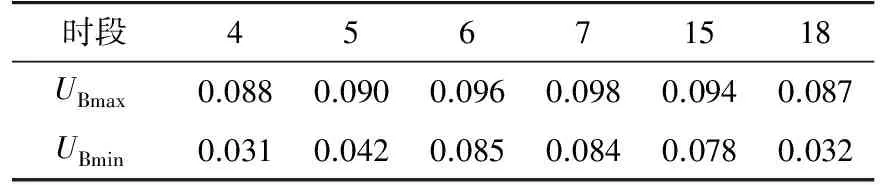
表3 风速波动较大时段UB的取值Tab. 3 Value of wind speed fluctuation period
4 结论
文中建立了考虑决策风险的计及风电和UPFC的多目标最优潮流模型,并通过IEEE-14节点进行算例分析验证模型的有效性,得到以下结论:
(1) 利用UPFC调节的快速性和灵活性可有效应对风电波动带来的不确定性,根据风速变化实时匹配预先得到的优化方案,为现代电网调度自动化系统提供了决策保障;
(2) 以经济性为目标的单目标优化有可能导致机组出力频繁或者大幅的调整,考虑决策风险性的多目标优化兼顾了经济性和机组的爬坡特性,从而尽可能减小了因风速变化过快而机组滞后响应而造成的停电风险。
[1] 孙元章, 吴 俊, 李国杰. 风力发电对电力系统的影响[J]. 电网技术, 2007, 31(20): 55-62.
SUN Yuanzhang, WU Jun, LI Guojie.Influence research of wind power generation on power systems[J]. Power System Technology, 2007, 31(20): 55-62.
[2] 王深哲, 高 山, 尤国伟, 等. 考虑多安全性约束的风电场穿透功率极限研究[J]. 电力工程技术, 2017, 36(3): 57-61.
WANG Shenzhe, GAO Shan, YOU Guowei, et al. Wind penetration limitation research considered multiple security constraints[J]. Electric Power Engineering Technology, 2017, 36(3): 57-61.
[3] 罗 钢,杨银国,钱 峰. 含风电场的电力系统动态关键输电断面分析[J]. 广东电力,2016,29(10):54-61.LUO Gang, YANG Yinguo, QIAN Feng. Dynamic key power transmission sections of power systems integrated with Wind farms[J]. Guangdong Electric Power,2016,29(10):54-61.
[4] 迟永宁, 刘燕华, 王伟胜, 等. 风电接入对电力系统的影响[J]. 电网技术, 2007, 31(3): 77-81.
CHI Yongning, LIU Yanhua, WANG Weisheng, et al. Influence of wind power integration on power system[J]. Power System Technology, 2007, 31(3): 77-81.
[5] 周 玲, 王 宽, 钱科军, 等. 计及UPFC的电力系统无功优化[J]. 中国电机工程学报, 2008, 28(4): 37-41.
ZHOU Ling, WANG Kuan, QIAN Kejun, et al. Reactive power optimization of power system considering UPFC[J]. Proceedings of the CSEE, 2008, 28(4): 37-41.
[6] 钱 臻, 刘建坤, 陈 静,等. 基于自动微分技术的含UPFC电力系统最优潮流[J]. 电网与清洁能源, 2016, 32(4): 24-29.
QIAN Zhen, LIU Jiankun, CHEN Jing, et al. Optimal power flow with UPFC based on automatic differentiation[J]. Power System and Clean Energy,2016, 32(4): 24-29.
[7] 祁万春, 杨 林, 宋鹏程,等. 南京西环网UPFC示范工程系统级控制策略研究[J]. 电网技术, 2016, 40(1): 92-96.
QI Wanchun, YANG Lin, SONG Pengcheng, et al.UPFC system control strategy research in Nanjing western power grid[J]. Power System Technology, 2016, 40(1): 92-96.
[8] 陈 刚, 李 鹏, 袁宇波. MMC-UPFC在南京西环网的应用及其谐波特性分析[J]. 电力系统自动化, 2016, 40(7): 121-127.
CHEN Gang, LI Peng, YUAN Yubo. Application of MMC-UPFC on Nanjing western grid and its harmonic analysis[J]. Automation of Electric Power Systems, 2016, 40(7): 121-127.
[9] ENRIGUE ACHA,CLAUDIO R FUERTE-ESQUIVEL,HUGO AMBRIZ-PEREZ,et al. FACTS modeling and simulation in power networks[M]. John Wiley & Sons Ltd,2004:200-216.
[10] KHOSRAVI A, NAHAVANDI S, CREIGHTON D, et al. Wind farm power uncertainty quantification using a mean-variance estimation method[C]∥ 2012 IEEE International Conference on Power System Technology (POWERCON). Auckland, 2012: 1-6.
[11] 刘燕武, 张忠桢. 基于实际收益率分布的均值-方差-条件风险价值多目标投资优化模型[J]. 系统管理学报, 2010, 19(4): 444-450.
LIU Yanwu, ZHANG Zhongzhen. Mean-variance-cvar portfolio optimization model based on real return distribution[J]. Journal of Systems and Management, 2010, 19(4): 444-450.
[12] ROMAN C, ROSEHART W. Evenly distributed pareto points in multi-objective optimal power flow[J]. IEEE Transactions on Power Systems, 2006, 21(2): 1011-1012.
[13] 陈 霜, 孙国强, 卫志农,等. 计及碳排放的含风电场电力系统随机可用输电能力协调决策[J]. 电网技术, 2016, 40(2): 405-411.
CHEN Shuang, SUN Guoqiang, WEI Zhinong, et al. Coordinated stochastic available transfer capability decision-making considering Carbon emission with wind Farm integration[J]. Power System Technology, 2016, 40(2): 405-411.
[14] Iowa Environmental Mesonet. AWOS download data[EB/OL].[ 2015-08-18]. http:∥mesonet.agron.iastate.edurequestawos1min.php. 2011-04-01.
[15] 钱 臻, 刘建坤, 陈 静, 等. 计及风电不确定性的含UPFC电力系统的两阶段最优潮流[J]. 电力自动化设备, 2017, 37(3): 80-86.
QIAN Zhen, LIU Jiankun, CHEN Jing, et al.Two stage optimal power flow of power system with UPFC considering wind power uncertainty[J]. Electric Power Automation Equipment, 2017, 37(3): 80-86.
[16] 罗 毅, 李昱龙. 基于熵权法和灰色关联分析法的输电网规划方案综合决策[J]. 电网技术, 2013, 37(1): 77-81.
LUO Yi, LI Yulong. Comprehensive decision-making of transmission network planning based on entropy weight and grey relational analysis[J]. Power System Technology, 2013, 37(1): 77-81.

