基于电力系统主导振荡模式提取的区域负荷模型识别研究
郝丽丽, 汪成根, 方 鑫, 谈怡君, 侯佳欣, 熊海波
(1. 南京工业大学电气工程与控制科学学院,江苏 南京 211816;2. 国网江苏省电力有限公司电力科学研究院,江苏 南京 211103;3. 国网丰县供电公司,江苏 丰县 221700)
0 引言
电力系统多次发生仿真结果无法复现事故真实情况的事件[1-5],仿真的有效性问题亟待解决。模型的不准确是导致仿真结果异于系统实际运行状况的关键因素之一。通过信息采集和状态估计,可获得较为准确的电力系统网络拓扑模型。系统额定运行状态下,线路、变压器、电容、电抗器等元件的模型参数较为准确,通过厂家测试、独立建模与定期跟踪检验,发电机及其控制器的模型也较为可靠。然而,作为电力系统重要元件之一的负荷,在发输电网中其模型通常是由负荷、变压器、电源、储能、补偿设备等值得到。系统中负荷数目繁多、接入分散,且负荷具有随机性和时变性,所以负荷很难逐一、准确建模,负荷模型较系统的其它元件更加不可信,是仿真误差的主要来源之一[6-8]。
将特征接近的空间负荷点归为一类,统一辨识各类负荷的方法兼顾了模型的准确性和计算效率[9-11]。负荷分类涉及负荷特征向量的选取与聚类,选取的样本特征应能完全体现样本的本质[12-14],且不影响识别结果的强壮性[15-16]。需要基于不同的聚类原则与实际需要选择合适的聚类方法[17-20]。此外,针对负荷的时变性,仿真系统中的负荷模型应能跟踪负荷实际变化,如何兼顾负荷的时间、空间分布规律,根据现场测量信息及时识别并自动更新负荷模型,建立更为准确的自适应负荷模型,是探讨的重点。
通过分析系统主导振荡模式选取观测母线,制定模型识别的目标函数,以负荷用电性质构成比例作为负荷节点的特征,对空间负荷进行分类,同类负荷采用相同的模型参数,用梯度优化算法对系统各类负荷进行统一识别。文中分别在IEEE 39和118节点系统上进行验证,结果表明以负荷用电性质构成比例进行分类,得到的负荷识别结果强壮性更好,同时展示了负荷时变分类阈值的选取方法。
1 基于负荷用电性质构成比例的负荷分类
1.1 分类特征的选取
就用电性质而言,负荷一般可分为工业、商业、农业、居民负荷及其他4类。各类负荷的特征一般比较固定,如商业负荷、居民及其他负荷包含比重较大的静态用电设备,而工业负荷中电动机负荷比重较大,农业负荷多为灌溉负荷。统计表明,各种性质负荷的恒阻抗负荷比例Ap,Aq,恒电流负荷比例Bp,Bq,恒功率负荷比例Cp,Cq和电动机负荷比例Kpm,Kqm具有较为固定的分布规律[21]。因此,可以根据各节点不同用电性质负荷构成比例得到近似的负荷模型参数。文中选取以上4种不同用电性质负荷占所接入负荷节点总负荷量的比例作为负荷节点的分类特征。一个样本周期内第s(s=1, 2,…,Ns)次采样得到的第i(i=1, 2,…,n)个负荷节点的负荷用电性质构成比例为Xi,s=(xis1,xis2,xis3,xis4),其中xis1,xis2,xis3,xis4分别表示第i个负荷第s次采样时工业、商业、农业、居民负荷及其他所占的用电比例。
大规模电力系统数字仿真中,负荷节点可能是多个实际负荷的聚合,也可能是由多个元件聚合等效并折算到中、高压侧母线得到。对于前者,事先详细分析负荷节点所接每个实际负荷用户的用电性质,再根据采集到的各负荷用户的实时接入情况,计算得到该负荷节点的实时负荷用电性质构成比例进行负荷分类;对于后者,则需逐一分析各类元件的性质,将其归为某类用电性质的负荷,并按照每个元件的电压等级进行容量折算,再计入各元件的实时接入情况,计算得到等效负荷节点的实时负荷用电性质构成比例。
1.2 基于模糊C均值聚类算法的负荷分类
文中采用模糊C均值聚类算法,依据1.1节中所选负荷特征,用隶属度函数判断n个负荷节点的聚类情况,得到系统总的负荷分类数目为C,并求取每类的聚类中心,使得类内加权误差平方和最小。用[0,1]间的隶属度μifi来确定第i个负荷特征属于第fi(fi=1,2,…,C)组聚类的程度,一个负荷点各组的隶属度总和为1。
(1)
式中:C为聚类数;n为负荷节点数;μifi为隶属度值。对负荷特征分类,优化C使得类内距离最小,类间距离最大。类内距离是指同类中与其类中心离差的平方和,表达式如下:
(2)
不同类的类间距函数表达式为:
(3)
式中:m为权值,1≤m≤∞;Xi为某次采样得到的第i个负荷的特征样本元素;Vfi,Vfj分别为第fi和fj类负荷的聚类中心,fi≠fj,Vfi表示如下:
(4)
基于模糊C均值聚类算法的负荷分类步骤为:

步骤(2):计算由隶属度的值所组成的划分矩阵U;
2 各类负荷节点的统一识别
2.1 观测母线的选取
选择能充分、有效反映系统关键动态行为的母线作为观测对象,比较观测对象上实测与模型仿真响应的差异程度,作为模型识别的目标函数。扰动可能激发系统的多种振荡模式,与主导振荡模式相关的母线信息能够反映模型对系统关键动态过程的影响。此外,电压级别高或关键节点变电站,尤其是位于联络线上的电站,对系统有更广泛的影响。如果这些电站仿真响应曲线与测量信息接近,则临近母线的仿真结果也会与实测接近。因此,在电力系统模型识别中,应选择那些充分参与系统主导振荡模式,且位于联络线上并具有较高电压等级的关键变电站母线作为观测对象。基于Prony法从实测信号中提取系统振荡模式,过程如下。
电力系统是一个高阶非线性系统,对于小扰动,我们一般将系统在运行点附近线性化为:
(5)
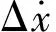
(6)
式中:Ri=ciφiψib,φi和ψi分别为特征根λi的左、右特征向量。当采样间隔Δt恒定时,yj(t)可以表示为下述离散形式:
(7)
式中:zi=exp(λiΔt),λi=σi+jω为模型阶数;n为未知量;第i个模式的参数zi;Ri可以通过Prony算法估算得到。
方程式(7)可以写成以下形式:
(8)
式中zi满足关于未知系数ai的n阶多项式的根:
zn-(a1zn-1+a2zn-2+...+anz0)=0
(9)
式(8)两侧左乘[-an,-an-1,...,-a1,1,0,...,0],可得到:
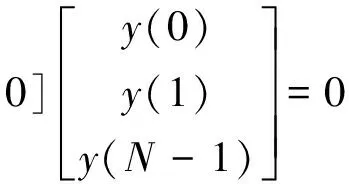
(10)
式(8)左乘[0,-an,-an-1,...,-a1,1,0,..,0],等式右侧结果也为0。重复式(9)的计算可得下式:

(11)
利用Prony法识别系统振荡可以同时对所有量测进行频率、阻尼比、模态的识别,概括为以下步骤:求解式(11)得到系数ai,求解式(7)的根得到zi,求解式(8)中的复数残差Ri,判别系统的主导振荡模式及模态,从而确定每个测点参与主导振荡的程度,进而选择模型识别的观测对象。
2.2 模型识别的目标函数
文中选用实际(或参考)系统与仿真(或模型)系统观测母线的电压均方误差作为负荷模型识别的目标函数J表达式为:
(12)
式中:N表示动态响应采样点数;Vm(j)表示观测母线的第j个电压实测值;Vs(j)表示仿真系统中观测母线的第j个电压响应。设置误差阈值εJ,若J>εJ,则表明当前负荷模型无效,需要进行广域电力系统负荷的空间分类及识别;反之,则表明当前模型有效。
2.3 待识别参数的选取
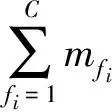
{{α11,α12,...,α1m1},{α21,α22,...,α2m2},...,
{αfi1,αfi2,...,αfimfi},...,{αC1,αC2,...,αCmC}}(13)
目标函数J关于负荷模型参数的灵敏度越大,表明该参数对变量的影响越大,可以优先识别这些灵敏度大的参数;反之,那些灵敏度小的参数,其调整对仿真结果影响微弱,可以用典型值进行替代,从而减少系统待识别参数的个数,减少计算量。
2.4 参数优化算法

(14)
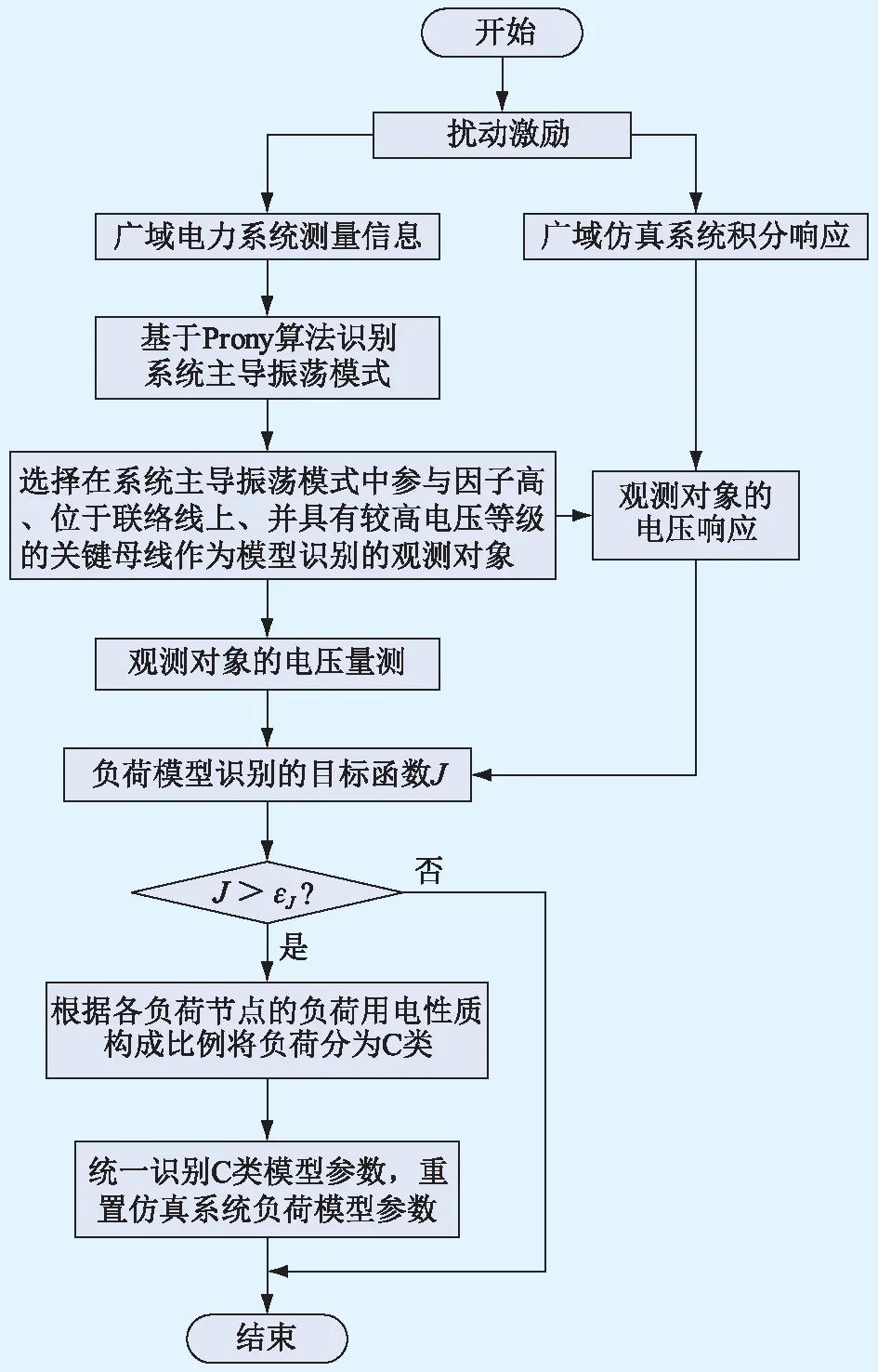
图1 电力系统负荷的识别模块流程Fig.1 Identification sub-module of power system load model
3 算例仿真
3.1 IEEE 39节点系统仿真
假设各节点感应电动机内部参数已明确,仅考虑负荷节点上各类静态负荷和动态负荷占总负荷大小的比例参数,其中Cp=1-Ap-Bp,Cq=1-Aq-Bq。故所需识别的参数为Ap,Aq,Bp,Bq,Kpm,Kqm。选用IEEE 39节点系统进行分析,选择负荷节点3,15,16,18,21,25—29为研究对象,它们各自的负荷用电性质构成比例如表1所示,根据文献[20]中各类负荷中静态和动态负荷的典型比例数据,得到这些负荷的综合模型参数,并将相应的系统仿真结果作为参考系统的实测值。

表1 IEEE 39节点系统的负荷用电性质构成比例Tab. 1 Proportion of consumption componentof loads of IEEE 39-bus system
基于文中所提特征对负荷分类并识别得到的负荷模型记为模型系统Ⅰ。为检验文中所提分类方法的优劣,选取了另外两种负荷分类策略,其一为按负荷间电气距离的大小分类,用该方法分类识别得到的负荷模型记为模型系统Ⅱ;其二为负荷节点不分类,即将待研究负荷节点设定为一类,且各节点具有相同的模型参数,识别得到的模型记为模型系统Ⅲ。设扰动场景为线路16—19距首端20%处发生三相短路,故障持续0.04 s。将系统中所有电压母线作为候选观察对象,对其响应曲线进行Prony振荡模式计算,结果显示系统发生约2.5 Hz的区间振荡,振荡模式如图2所示,多条母线参与程度均较为接近,其中红色为母线BUS16,绿色和蓝色代表其余母线,因该算例系统无法体现电压的有名值情况,因此,选取了参与振荡程度较好且跌落最严重的母线BUS16作为系统区域负荷模型识别的观测母线。
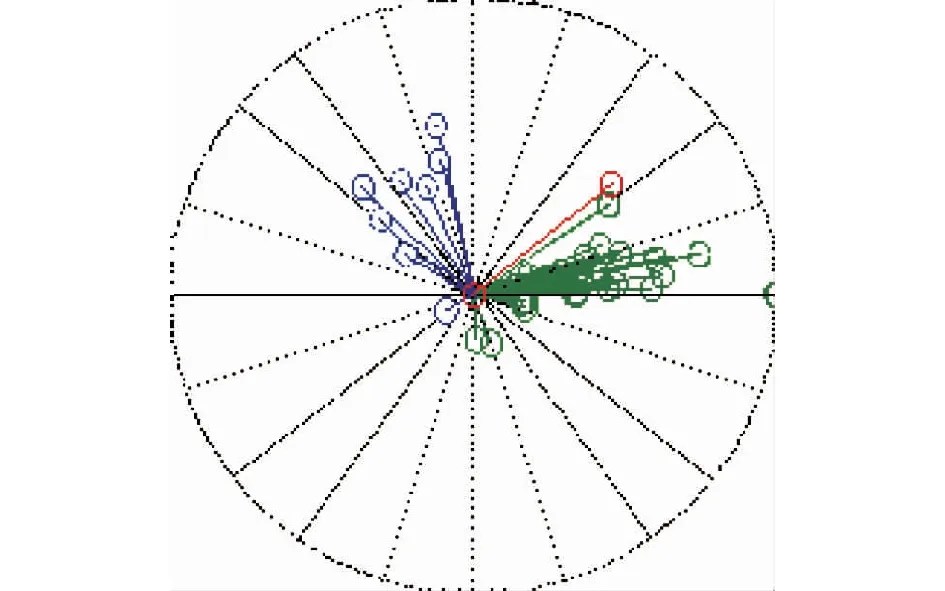
图2 系统主导区间振荡模式分析Fig.2 Mode shape of dominant interarea mode
根据各节点负荷用电性质构成比例,基于聚类算法将负荷分为3类:第Ⅰ类为负荷3, 16, 21, 25;第Ⅱ类为负荷15, 26, 27;第Ⅲ类为负荷18, 28, 29。每类负荷待识别参数为Ap,Bp,Aq,Bq,Kpm,Kqm,经灵敏度计算,参数Ap,Kpm,Kqm的灵敏度最高,将它们选取为待识别参数,则系统需识别的负荷参数共9个,为Apfi,Kpmfi,Kqmfi(fi=1,2,3),其余参数取典型参数值代替,模型系统I的负荷参数识别结果见表2。

表2 按负荷用电性质比例分类识别的负荷参数Tab. 2 Identification results of load model using theproportion of load consumption componentas the classification characteristics
依据负荷节点间的电气距离将负荷分类为:3, 15, 21, 26, 27为第Ⅰ类;16, 18, 25为第Ⅱ类;28, 29为第Ⅲ类。在相同的扰动场景下进行参数识别,得到模型系统Ⅱ的负荷参数结果。设所有负荷都有相同的模型参数,在相同的扰动场景下进行参数识别,得到模型系统Ⅲ的负荷参数结果。图3给出了模型系统Ⅰ—Ⅲ与参考系统的电压响应。结果表明,不分类识别对应的仿真响应误差最大,以节点间电气距离分类识别得到的结果,其误差次之,以负荷用电性质特征分类识别的模型,其响应与参考系统的电压轨迹拟合很好。

图3 参考系统和模型系统的观测对象电压响应Fig.3 Voltage response of reference and model systems
在某一特定运行场景下识别得到的模型参数能否在其他场景下也较好的反映元件动态,即模型的适用性问题,需要进一步检验。各负荷大小及组成保持不变,分别改变系统扰动强度、扰动位置、系统潮流分布和网络拓扑结构,检验在某运行场景中识别得到的模型系统Ⅰ—Ⅲ的参数对其他运行场景的适用性。
(1) 扰动强度影响的检验。扰动场景为线路16—15距首端30%处发生三相短路,扰动持续时间τ。τ分别取为0.04 s,0.045 s,0.05 s。BUS15为参考系统观测母线,当τ=0.04 s时的电压响应曲线如图4所示,模型系统Ⅰ与参考系统的电压响应基本重合,模型系统Ⅱ的电压响应与参考系统拟合略差,而模型系统Ⅲ的响应曲线与参考系统响应差别最大,其主导振荡模式频率明显增加。表3给出了τ取不同值时的响应误差J,随着扰动强度的增加,各模型系统误差值J都在不断增大,也显示出模型系统I的误差值J总能保持在相对较小的范围,而模型系统Ⅲ的误差值最大。

图4 τ=0.04 s时模型与参考系统电压响应Fig.4 Voltage response of model and reference system while τ=0.04 s

表3 扰动强度变化时的响应误差Tab. 3 Response error changedwith the duration of disturbance
(2) 扰动位置影响的检验。扰动场景取为线路16—15距首端x%处发生三相短路,持续时间为0.04 s。分别取x为10, 20, 50,BUS15仍为参考系统观测母线。图5给出了当x=10时的电压响应。表4给出了故障发生在不同位置时各模型系统与参考系统的电压误差值J。模型系统Ⅰ与参考系统电压响应的接近程度明显优于模型系统Ⅱ和Ⅲ,且当扰动地点变化时,模型系统Ⅰ的适用性更好。

图5 x=10时模型与参考系统电压响应Fig.5 Voltage response of model and reference system while x=10
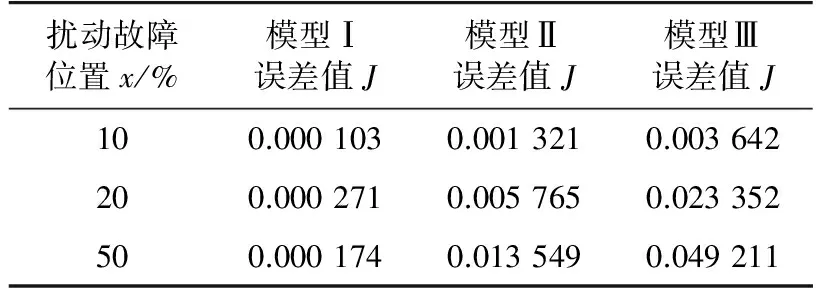
表4 扰动位置变化时的响应误差Tab. 4 Response error changedwith the disturbance location
(3) 系统潮流分布影响的检验。在原始系统的基础上,仅改变部分机组出力,如表5所示,得到系统的潮流分布Ⅰ—Ⅲ,记初始有功功率为P0,调整后的有功功率为P。扰动场景仍为线路16—15距首端30%处发生三相短路故障,持续时间为0.04 s,BUS15为观测母线。图6给出了系统潮流分布为情况Ⅰ时模型系统和参考系统的电压响应,表6给出了当潮流分布改变后,各模型系统与参考系统的电压误差值J。结果显示,虽然潮流分布变化,但模型系统Ⅰ仍然可以很好的反映参考系统的动态,模型系统Ⅱ和Ⅲ的响应却与参考系统有较大差距。
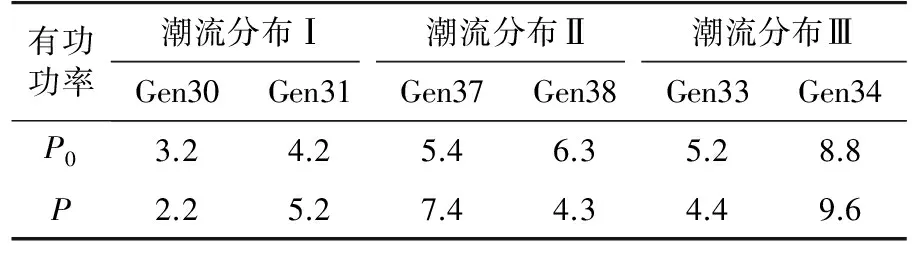
表5 潮流分布情况I—ⅢTab. 5 Power flow distribution I—Ⅲ

图6 潮流分布I下模型与参考系统电压响应Fig.6 Voltage response of model and reference system with flow distribution I
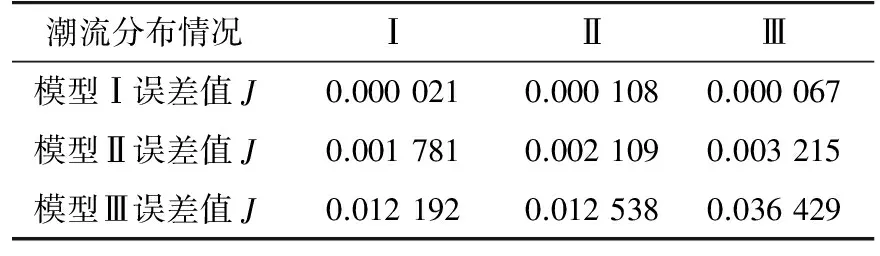
表6 潮流分布变化时的响应误差Tab. 6 Response error with flow distribution changed
(4) 网络拓扑结构影响的检验。在原始系统基础上仅切除线路5—6得到拓扑结构Ⅰ,仅切除线路13—14得到拓扑结构Ⅱ,仅切除线路6—11得到拓扑结构Ⅲ。扰动场景为线路16—15距首端10%处发生三相短路,扰动持续时间为0.03 s。BUS15为观测母线。图7给出了拓扑结构Ⅰ时系统的电压响应,表7给出了当拓扑改变后,各模型系统与参考系统的电压误差J。结果表明模型系统Ⅰ适应其他拓扑结构的能力更强。

图7 拓扑结构I下模型与参考系统电压响应Fig.7 Voltage response of model and reference system with grid topology I

表7 网络拓扑结构变化时的响应误差Tab. 7 Response error changed with the grid topology
综上,当保持各节点负荷的大小和组成不变,仅改变系统其他运行条件,按负荷用电性质构成比例分类得到的参数识别结果具有良好的精度和适用能力,远优于按负荷节点所属区域分类和不分类两种情况下的识别结果,而不分类的负荷模型识别结果,其精度和适用性最差。
3.2 IEEE 118节点系统仿真
本节选取IEEE 118节点系统再次对上述分类识别方法进行检验。选取27个负荷节点作为研究对象,各节点负荷用电性质构成比例如表8所示。扰动场景为线路6—7距首端母线30%处发生三相短路,持续时间为0.05 s,将系统中220 kV以上电压母线作为候选观察对象,对其响应曲线进行Prony振荡模式计算,结果显示系统发生约0.4 Hz的区间振荡,振荡模式如图8所示,其中红色为500 kV 母线BUS20,位于区域间的联络线上,绿色和蓝色代表其余母线,鉴于BUS20充分参与了系统的区间振荡,且电压等级高,因此将其选为系统区域负荷模型识别的观测母线。以负荷用电性质构成比例分类,结果如表9所示,经过灵敏度计算,参数Ap,Bp,Kpm的灵敏度较大,表10给出了模型参数的识别结果。

表8 IEEE 118节点系统的负荷用电性质构成比例Tab. 8 Proportion of load consumption component ofloads in IEEE 118-bus system
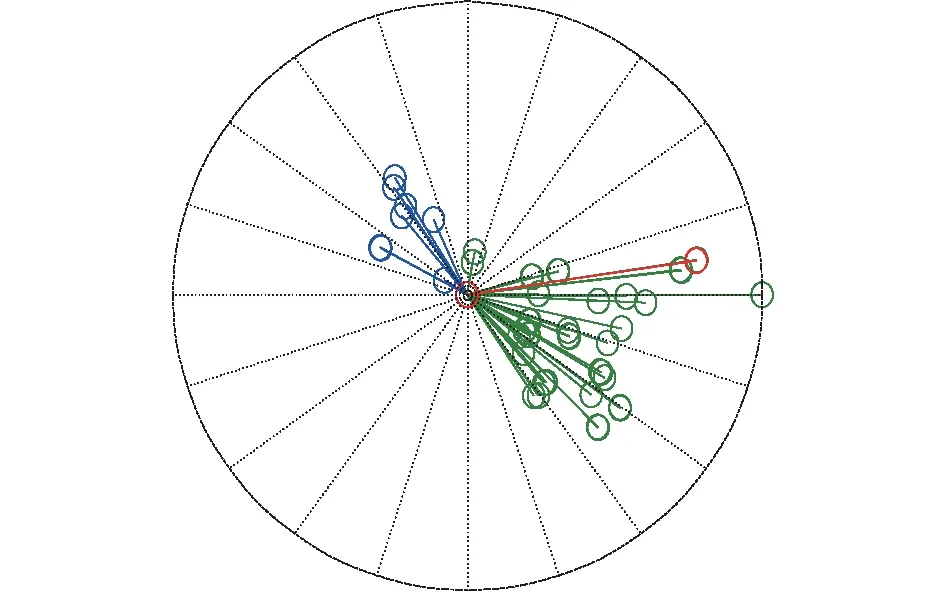
图8 系统主导区间振荡模式分析Fig.8 Mode shape of dominant interarea mode

表9 根据负荷用电性质构成比例进行分类Tab. 9 Load classification based on proportionof load consumption component

表10 按负荷用电性质比例分类识别的负荷参数Tab. 10 Identification results of load model usingthe proportion of load consumption component as theclassification characteristics
同4.1节,选用不同分类特征对负荷分类识别得到的模型系统响应曲线如图9所示。通过计算,模型系统Ⅰ、Ⅱ和Ⅲ与参考系统的响应误差值J分别为0.000 401,0.000 913,0.001 124,该算例进一步说明文中所提负荷分类识别方法的有效性。
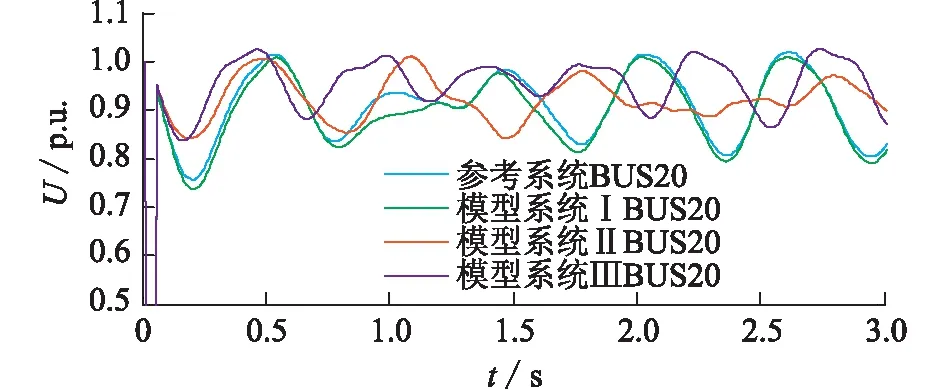
图9 参考系统和模型系统的电压响应Fig.9 Voltage response of reference and model system
5 结语
选取不同用电性质负荷占所接入负荷节点总负荷量的比例作为负荷节点的分类特征,采用模糊C均值聚类算法对负荷节点进行分类,认为同一类负荷节点具有相同的负荷参数,进行负荷模型识别。为了在不增大观察维度的前提下充分反映区域负荷对电网动态的整体影响,利用Prony算法从实测信号中提取系统振荡模式,并识别其中的主导振荡模式,用参与主导振荡模式的高电压级别母线作为观测母线,并用观测母线的电压建立参数识别的目标函数及主导参数的选择方法,用优化算法对主导参数寻优,获得负荷模型。在IEEE 39节点和IEEE 118节点系统上进行检验,通过多种分类策略下的负荷参数识别结果优劣的比较,表明按负荷用电性质构成比例分类识别的方法,得到的负荷模型识别结果具有更好的适用性。
[1] 郝丽丽, 岳浩永, 张恒旭, 等. 分类策略对广域系统负荷识别结果适应性的影响分析[J]. 电网技术, 2014, 38(2):381-387.
HAO Lili, YUE Haoyong, ZHANG Hengxu, et al. Influence analysis of classification strategy on wide area system load identification result adaptablity [J]. Power System Technology, 2014, 38(2): 381-387.
[2] WALVE K. Modeling of power system components at severe disturbances[C]∥CIGRE Meeting, Paris, France, 1986.
[3] KOSTEREV D N, TAYLOR C W, MITTELSTADT W A. Model validation for August 10, 1996 WSCC system outage[J]. IEEE Transactions on Power Systems, 1999, 14(3): 967-979.
[4] VENKATASUBRAMANIAN V, LI Y. Analysis of 1996 Western American electric blackouts[C]∥Bulk Power System Dynamics and Control-VI, Cortinad Ampezzo, Italy, 2004.
[5] 方勇杰. 美国9.8大停电对连锁故障防控技术的启示[J]. 电力系统自动化, 2012, 36(15): 1-7.
FANG Yongjie. Lessons from September 8, 2011 southwest America blackout for prevention and control of cascading outages [J]. Automation of Electric Power Systems, 2012, 36(15): 1-7.
[6] CHICCO G. Overview and performance assessment of the clustering methods for electrical load pattern grouping[J]. Energy, 2012, 42(1):68-80.
[7] 鞠 平, 金 艳, 吴 峰, 等. 综合负荷特性的分类综合方法及其应用[J]. 电力系统自动化, 2004, 28(1):64-68.
JU Ping, JING Yan, WU Feng, et al. Studies on classification and synthesis of composite dynamic loads [J]. Automation of electric power systems, 2004, 28(1):64-68.
[8] MAHMOUDI-KOHAN N. An annual framework for clustering-based pricing for an electricity retailer[J]. Electric Power Systems Research, 2010, 80(9):1042-1048.
[9] 郑晓雨, 贺仁睦, 马 进, 等. 基于轨迹灵敏度的负荷分类[J]. 电工技术学报, 2010, 25(9):145-150.
ZHENG Xiaoyu, HE Renmu, MA Jin, et al. A method of load classification based on the trajectory sensitivity [J]. Transactions of china electro technical society, 2010, 25(9):145-150.
[10] 李欣然, 林舜江, 刘杨华, 等. 基于实测响应空间的负荷动特性分类原理与方法[J]. 中国电机工程学报, 2006, 26(8):39-44.
LI Xinran, LIN Shunjiang, LIU Yanghua, et al. A new classification method for aggregate load dynamic characteristics based on field measured response [J]. Proceedings of the CSEE. 2006, 26(8):39-44.
[11] 石景海, 贺仁睦. 动态负荷建模中的负荷时变性研究[J]. 中国电机工程学报. 2004, 24(4):85-90.
SHI Jinghai, HE Renmu. Load time-variantion study in dynamic load modeling[J]. Proceedings of the CSEE. 2004, 24(4):85-90.
[12] 张红斌, 贺仁睦, 刘应梅. 感应电动机负荷模型参数灵敏度分析及参数辨识策略研究[J]. 电网技术, 2004, 28(6):10-14.
ZHANG Hongbing, HE Renmu, LIU Yingmei. Analysis on parameter analytic sensitivity of induction motor load model and parameter identification strategy [J]. Power System Technology, 2004, 28(6): 10-14.
[13] 鞠 平, 陈 谦, 熊传平, 等. 基于日负荷曲线的负荷分类和综合建模[J]. 电力系统自动化, 2006, 30(16): 6-9.
JU Ping, CHEN Qian, XIONG Chuanping, et al. Load clustering and synthetic modeling based on daily load curves [J]. Automation of electric power systems, 2006, 30(16):6-9.
[14] WANG Z S, BIAN S R,et al. The load characteristics classification and synthesis of substations in large area power grid[J]. International Journal of Electrical Power and Energy Systems, 2013, 48(1):71-82.
[15] 汪小明, 刘涤尘, 吴 军, 等. 电力系统暂态稳定分析广义负荷模型[J]. 电网技术, 2011, 35(3):44-48.
WANG Xiaoming, LIU Dichen, WU Jun, et al. A generalized load model for transient stability analysis of power system [J]. Power System Technology, 2011, 35(3):44-48.
[16] 朱建全, 李 颖, 谭 伟. 基于特性融合的电力负荷建模[J]. 电网技术, 2015, 39(5):1358-1364.
ZHU Jianquan, LI Ying, TAN Wei. Characteristic fusion based on electric load modeling [J]. Power System Technology, 2015, 39(5):1358-1364.
[17] 申定辉,于晓蕾,吴 丹. 基于混合高斯模型的配电网负荷伪量测权重优化算法[J]. 广东电力,2016,29(5):86-91,123.
SHEN Dinghui, YU Xiaolei, WU Dan. Optimization algorithm for pseudo measurement weight of power distribution network load based on Gaussian mixture model[J]. Guangdong Electric Power,2016,29(5):86-91,123.
[18] HAN D, MA J, HE R M, et al. A real application of measurement-based load modeling in large-scale power grids and its validation[J]. IEEE Transactions on Power Systems, 2009, 24(4): 1756-1764.
[19] 黄 梅, 贺仁睦, 杨少兵, 等. 东北电网负荷模型的分类与应用[J]. 电力系统自动化, 2005, 29(4):85-87.
HUANG Mei, HE Renmu, YANG Shaobing, et al. Application of load model classification in northeast power network [J]. Automation of Electric Power Systems, 2005, 29(4):85-87.
[20] 张树卿, 韩英铎, 于松泰, 等. 区域综合负荷动态等值参数在线测辨关键技术[J]. 电力系统自动化, 2012, 36(19):114-121.
ZHENG Shuqing, HAN Yingduo, YU Songtai. et al. Key techniques for composite load area integral equivalence and online parameter identification [J]. Automation of Electric Power Systems, 2012, 36(19):114-121.
[21] 鞠 平. 电力系统负荷建模理论与方法[M]. 北京: 科学出版社, 2010.
JU Ping. Power system load modeling theory and method[M]. Beijing:Science Press,2010.

