大跨PC箱梁0#块收缩徐变效应分析

苟红兵

(1.辽宁大通公路工程有限公司，辽宁 沈阳 110111;2.辽宁省交通规划设计院有限责任公司 公路养护技术研发中心，辽宁 沈阳 110166)

在全预应力混凝土桥梁施工中，能够获得悬臂梁在施工过程中的真实受力情况，了解结构的健康状况，这也是工程技术人员关心的核心问题。目前，国内桥梁监控人员在桥梁施工监控中，对应力的监控主要是在混凝土中预埋应变传感器，以此监测结构在施工过程中的受力变化情况。而如何从所采集的应变中扣除无应力应变、提取出结构的真正受力应变，是目前桥梁应力监控人员需要解决的主要问题。这些无应力应变主要有:应变传感器自身因素[1-3]、结构收缩效应、结构徐变效应[4-7]、温度效应[8-9]、钢筋对徐变的影响[10]、混凝土弹性模量随时间变化效应6个方面。

通过过去几十年人们对预应力钢筋混凝土的研究，取得了许多宝贵的研究成果[11-13]，在对混凝土结构的试验、检测、数据分析[14]方面都有较大突破，对预应力混凝土本构关系的认知更加接近实际。本文在前人研究的基础上，以大连渤海大道沿线的普湾大桥为实例，对悬臂施工过程中混凝土箱梁的0#块温度效应、收缩徐变效应分别进行现场试验研究和全过程分析，为混凝土0#块箱梁的施工和设计提供参考。

1 理论基础

1.1 温度应变

温度应变包含两方面：一方面为弦式传感器在温度变化下自身的变化；另一方面为混凝土本身受温度变化所产生的变化。传感器温感应变系数αm由传感器厂商提供或在传感器中埋入混凝土前进行实测[15-16]。混凝土线膨胀系数αc由《公路桥涵设计通用规范》(JTG D60-2004)取得，计算式为

(1)

文中αm通过现场实测，取值为2.2με/℃，αc取规范值0.000 010。则温度应变为传感器自身温度应变与混凝土自身温度应变的组合

εtm=αmΔt，

(2)

(3)

εt=εtm+εtc.

(4)

式(2)中Δt为测量时传感器温度读数与结构温度初读数的差值，式(3)中li为每次计算步长，Δti为计算步长范围内主梁板温差，l为计算梁长。

1.2 收缩应变

根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62-2004)附录F，混凝土收缩应变值为

εcs(t,t0)=εcs0[βs(t-ts)-βs(t0-ts)]，

(5)

(6)

其中εcs0根据附录F，按照现场实测湿度取值，其他的混凝土尺寸，各工况施工日期需要现场技术

人员根据进度实时采集。

1.3 徐变应变

根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62-2004)附录F，混凝土徐变应变值为

φ(t,t0)=φ0.βc(t-t0)，

(7)

(8)

ε(t)=ε(τ0).(1+φ(t,τ0)).

(9)

其中的φ0根据附录F进行插值计算或根据现场实际情况进行计算，式中的相关参数需要技术人员现场采集，才能保证计算结果的准确性。

而混凝土悬臂梁浇筑过程中逐段浇筑、张拉，简化为荷载计算时属于逐级加载混凝土的徐变计算，应考虑加载的级数及每级加载时的混凝土龄期，因此，现场实际弹性应变值的递推公式为

(10)

(11)

式中：i为施工工况，εi为i工况下传感器实测应变，εci为i工况下收缩应变，εti为i工况下温度应变。

2 实桥混凝土应变分析

普湾大桥桥孔布置为70 m+5×120 m+70 m，采用预应力混凝土悬浇变高度连续箱梁。全桥分为左右幅，每幅设置31个监测截面，各监测截面分别位于各墩0#块大小桩号两侧、L/4处及各合拢段处，每个截面设置6个测点，每测点传感器选用应变与温度集成传感器，对温度和应变同时进行监测。传感器总体布置如图1所示，各断面布置如图2所示。传感器断面命名规则为Sn-k，其中n为墩号(n的取值为8～13)、k为断面位置(k取值为0、0′、L/4、L′/4,对应为小桩号0#块、大桩号0#块、小桩号L/4、大桩号L/4)。

图1 大桥应变监测截面布置图(单位:cm)

本文以普湾大桥左幅的10#墩0#块箱梁为原型，进行为期160 d的混凝土无应力状态下的收缩应变研究。以右幅8#墩0#块箱梁为原型，进行为期120 d的预应力混凝土箱梁单次加载(0#块张拉完成)状态下的收缩徐变应变研究。

2.1 收缩应变实测

本文选取左幅10#墩0#块箱梁为无应力状态自由收缩研究对象。左幅10#墩0#块箱梁施工方式为托架施工，浇注时间为2014-10-15。为进行混凝土箱梁收缩效应研究，通过征求施工单位意见，在不耽误工期的前提下，将左幅10#墩0#块箱梁的预应力张拉时间延后至2015-04-03。混凝土浇筑前在支座中心对应的箱梁横断面处埋设6个温度和应变合成的长期性较好的正弦式应变计，测试箱梁的纵向收缩，传感器布设方式如图2所示。对该断面的传感器数据以每10 d为单位，进行为期160 d的混凝土收缩效应数据采集，并对采集的数据按照式(2)～式(4)进行了温度修正，修正后收缩应变随时间的增加而发生变化(见图3)。

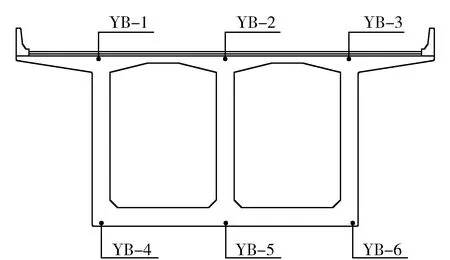
图2 应变及温度测点

图3 左幅10#墩支点断面收缩变化曲线

从图3可以看出，箱梁顶底板收缩效应明显不同，总体呈现出：顶板收缩效应>理论值>底板收缩效应的规律。主要由于顶板面积大于底板面积和顶板受阳光直射混凝土表面水分子交换速度快，顶面湿度低于底面湿度。顶面干缩速度快于底面干缩速度，呈现出收缩效应的大致规律为：底板为顶板的一半，顶底板均值与理论值较为接近。顶底板收缩应变时曲线呈现出线性变化趋势，160 d后顶板收缩应变为-10 με，底板收缩应变为-5 με。

2.2 徐变应变实测

右幅8#墩0#块箱梁施工方式为托架施工，浇注时间为2015-05-07，张拉时间为2015-10-24。对S8-0和S8-0′断面进行为期150 d的预应力张拉，完成状态下的徐变效应研究。对这两断面的传感器数据每10 d进行一次采集，并对采集的数据进行温度修正和收缩修正。修正后徐变应变随时间的增加量而变化，如图4所示。对图4顶底板徐变应变进行曲线拟合，拟合结果如图5所示。

图4 0#块徐变变化时程曲线

图5 0#块徐变应变曲线拟合

如图4所示，箱梁在前期徐变速度较快，随着时间的增长徐变速度逐渐减慢，到达100 d以后徐变变化率趋于稳定。

顶板拟合方程为

f(x)=0.617-0.795x+0.005 9x2-

0.000 001 6x3.

(12)

底板拟合方程

f(x)=0.803x+0.004 59x2-0.000 001x3.

(13)

由拟合结果可知，混凝土箱梁顶底板拟合结果符合三次多项式曲线,顶底板拟合结果系数R2均为0.98，拟合优度较好。150 d后顶板徐变应变为-53 με，底板徐变应变为-42 με。由于0#块顶板钢绞线布置呈凸形，箱梁中上部腹板预应力大于底板预应力，所以顶面预应力徐变值大于底板。

3 有限元仿真分析

为验证实测数据的有效性，对0#块建立有限元模型。分别计算其在无应力状态下的自由收缩应变、有初拉力状态下的收缩徐变应变和升降温状态下的应变变化。取现场实验室提供的10～150 d混凝土弹性模量为等效弹性模量，在实际模型中混凝土各时间段内的弹性模量以等效弹性模量代替。收缩系数和徐变系数按照《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62-2004)的公式计算，徐变系数和等效弹性模量的时程曲线如图6、图7所示。

图6 徐变系数时程曲线

图7 弹性模量时程曲线

0#块截面为单箱双室，腹板为直腹板，梁长为12 m，在主梁中心位置布设一道2.5 m长的横梁。梁高从距支座中心3～6 m处按照1.8次抛物线变化规律由7.8 m变为7.2 m，从距支座中心0～3 m处、高度为7.8 m的等高梁截面。箱梁顶宽度为16.5 m、底宽10.5 m，两侧翼缘悬臂长为3 m。顶板厚度为0.28 m，底板厚度为0.8 m。在距支座3 m 处两侧各设有0.5×10 m2的临时固结。实际建模过程中平面有限元模型采用25个节点，24个杆系单元。考虑直径为7 mm的纵向预应力束129根。边界条件中，支座提供竖向约束，临时固结提供三向约束，有限元模型和结果分析如图8～图12所示。

图8 有限元模型

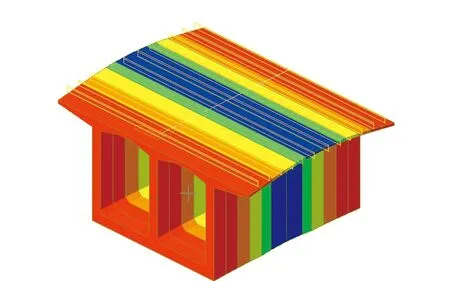
图9 正温度梯度效应

图10 150 d收缩徐变效应

图11 140 d自由状态下收缩效应

图12 8#墩0#块上下缘应变对比

由图9可知，结构在正温度梯度作用下呈现出顶板受拉现象，结构呈下挠趋势，结合规范JTG D60-2004可知，结构在负温度效应下呈现出正温度梯度相反、且效应减半的结果。由图10可知结构在150 d后的徐变效应为顶板效应大于底板效应，结构呈上挠趋势。由图11可知结构在160 d后的收效应不明显。对比图9～图11可知150 d后预应力箱梁的徐变效应、收缩效应和温度效应三者的大小关系为：徐变效应>温度效应>收缩效应。由图12和表1比较得出：JTGD62理论值介于顶底板之间，与顶板误差范围在-13%～5%, 与底板误差范围在-7%～19%。有限元软件与实测值相比较为接近，顶板有限元软件模拟值除了一天为-25%外，其余值与实测值误差范围均在-6%～13%, 底板有限元软件模拟值与实测值误差范围在-9%～7%。表明有限元软件在计算时将单元细化后的计算结果更加符合实际，同时也表明现场采集的数据与理论值较为吻合。顶底板实测值对比可以得出，顶板徐变量大于底板徐变量，导致结构有上挠的趋势和底板拉应力超限产生裂缝的可能。说明在实际施工过程中工程技术人员应合理安排施工工期，避免0#块的长时间搁置，设计人员应考虑在底板配置一定量的普通防裂钢筋。

表1 右幅8#墩0#块截面应变结果比较 με

4 结 论

本文以普湾大桥为例，基于现场实测数据、有限元理论分析的徐变模型，分析0#块箱梁在无应力状态下的自由收缩规律、预应力张拉完成后的徐变规律，可推导出以下结论：

1)自然状态下顶板收缩速率大于底板收缩速率，但收缩量约为徐变量的0.1倍。

2)150 d后预应力箱梁的徐变效应、收缩效应和温度效应三者的大小关系为：徐变效应>温度效应>收缩效应。

3)有限元软件在计算徐变时,单元细化后的计算结果更符合实际，顶板的徐变量>底板的徐变量,使结构有上挠的趋势和底板拉应力超限产生裂缝的可能。说明在实际设计和施工过程中工程技术人员应合理设计底板钢筋，合理安排施工工期，避免0#块的长时间搁置。

[1] 杨雅勋，李子青，郝宪武，等.预应力混凝土连续刚构桥主梁应力测试技术研究[J].铁道建筑，2007(8): 1-4.

[2] 苟红兵，胡铁明，张冠华，等.辽河大桥钢箱梁疲劳应力特性[J].沈阳大学学报，2015(4)：318-323.

[3] 汪剑，方志.大跨预应力混凝土箱梁桥收缩徐变效应测试与分析[J].土木工程学报,2005,41(1):70-81.

[4] 韩伟威,吕毅刚.混凝土收缩徐变预测模型试验研究[J].中南大学学报(自然科学版),2016(10):3515-3522.

[5] 李建慧,李爱群.混凝土结构收缩徐变效应随机分析[J].工业建筑,2016(9):76-80，55.

[6] 茹毅,刘其伟.收缩徐变作用下混凝土连续箱梁拼宽桥拼接段受力性能研究[J].中外公路,2016(2):196-200.

[7] 张玉,卢鑫宇,梁壮壮,等.大跨结构温度和应力的监测分析[J].交通科技与经济,2015，18(6):97-100，110.

[8] 胡铁明,苟红兵,张冠华,等.寒冷地区特大扁平钢箱梁温度及纵向应力分析[J].世界桥梁,2015(3):63-68.

[9] 曾庆响.大跨度预应力混凝土箱梁桥收缩徐变及温度效应的数值试验研究[D].广州：华南理工大学,2015.

[10] 王莹峰.桥梁施工监控中实测应力计算方法及MALAB实现[J].交通科技与经济,2015，17(6):117-121.

[11] 文永奎，陈政清.考虑预应力损失的混凝土梁徐变计算方法[J].中国铁道科学,2005(3):36-41.

[12] 孟江,赵宝俊,刘建梅.混凝土收缩徐变效应预测模型及影响因素[J].长安大学学报(自然科学版),2013(2):56-62.

[13] 潘钻峰,吕志涛,刘钊,等.高强混凝土收缩徐变试验及预测模型研究[J].公路交通科技,2010(12):10-15,32.

[14] 颜东煌,田仲初,李学文,等.混凝土桥梁收缩徐变计算的有限元方法与应用[J].中国公路学报,2004(2):56-59.

[15] 周舟.预应力混凝土箱梁桥中混凝土收缩徐变的影响研究[D].长沙：长沙理工大学,2006.