机场罐式加油车服务调度双目标优化研究

王 璐 张小宁 隋 杨 吴 辉

(1. 上海民航职业技术学院，上海 200232；2. 同济大学 经济与管理学院，上海 200092；3. 东华大学 旭日工商管理学院，上海 200051)

1 引言

近年，随着民航业的快速发展，机场规模和业务量日益扩大，繁忙机场面临的运行效率较低、地面设备调配不足的瓶颈问题日益突出。快速应对机场基本业务，不仅能保障航班正常运行、提高乘客满意度，也能有效降低机场与航空公司的成本，使场面作业高效运行。如何在资源设备有限的情况下，充分利用现有资源快速完成地面作业，是当前机场与航空公司共同面临的问题之一。

航班地面服务是机场运行的重要环节。航班地面服务调度主要指对各种航班地面保障车辆的合理调度。在大型枢纽机场，航班的起落具有短时、高密度的特点，对地面服务的需求较为集中，调度不当有可能造成航班延误，造成不必要的损失。地面设备作业具有严格的流程性，如加油车因存在安全隐患，只有当加油服务完成后才能进行上客服务，且不同类型航班所需的服务时间不同，因此保障加油车的合理调度为实现后续地面正常作业奠定了基础。

目前，关于机场地面服务的调度问题，国内外已有很多的研究。Angus Cheung等(2005)[1]以最小化车辆总流转时间为目标，分别进行了牵引车、清水车、清洁车的单独调度。王博涛(2006)[2]采用分解策略和多目标权衡策略将机场站坪调度分为机位指派和机坪保障设施调度问题。郑洁等(2008)[3]研究了机场服务设备的利用率问题，运用妥协约束法和遗传算法使得设备总流经时间最少。Xing Z等(2012)[4]基于博弈论对机场除冰车的调度进行了研究。Norin A等(2012)[5]以最小化由除冰服务引起的航班延误、最小化除冰车的行驶距离为目标对除冰车的优化调度进行了研究。杨文东等(2013)[6]以最小化车辆工作量、车辆行驶距离和车辆数为目标，建立了机场摆渡车的调度仿真模型。黄鹂诗(2013)[7]采用了SIMIO分别对加油车和摆渡车的调度进行仿真，以平衡设备工作量和航班延误最少为优化目标建立了优化模型。Jia Yan Du等(2014)[8]研究了航班过站作业中的拖车作业调度，以最小化运营成本为优化目标、以拖车运营限制为约束建立了MIP模型，使用了列代启发式算法对模型进行求解。冯霞等(2016)[9]以至少需要的保障车辆数目和服务总开始时间最早为目标，研究构建了远机位航班加油服务和上客服务的协同调度模型，并给出了基于多目标遗传算法的模型求解。

本文在研究机场罐式加油车为航班加油服务问题的基础上，建立了考虑每架航班所在停机位与机场加油站之间的距离和加油车在停机位之间的移动时间在内的整数规划模型，提出了以最小化完成航班加油服务时间和最小化航班等待加油时间的双目标规划模型，进而开发epsilon约束算法精确求解所建立的双目标规划模型获得Pareto前沿，并通过数值例子说明模型的有效性和算法可行性。文章在第二部分详细介绍了本文所研究的问题并构建了整数规划模型；第三部分设计了epsilon约束算法；第四部分以一个算例验证了模型的可行性和算法的有效性并最后给出结论。

2 问题描述和模型构建

2.1 问题描述

为保证航班的正常安全飞行，航班在机场过站期间需接受一系列的地面服务，此时机场相关部门会调用机场地面设备开始对航班进行一系列的地面服务，地面设备有行李车、加油车、摆渡车等。机场在一个时段内会有多个航班停靠在不同的停机位，当航班停靠稳定，地面设备开始作业。加油车不同于行李车、摆渡车等，加油车存在一定的安全隐患，航班需完成下客服务后再进行加油服务。因此，当航班完成下客服务后，罐式加油车开往飞机机翼加油处，将罐内的航空燃油安全、快速地输入飞机油箱。现机场大部分停机位有机井口，航班加油可通过管线加油车直接加油，少数停机位没有机井，需要使用罐式加油车为航班加油。因罐式加油车容量有限，一次最多只能服务有限个航班，当前多数机场的罐式加油车一次可服务至少两架航班，所以如何使机场加油车以尽可能低的成本高效率地完成地面加油服务作业，同时降低航班因机场地面作业延误而带来的经济损失，提高航空公司的服务质量，是目前机场亟需解决的问题，也是本文的研究重点。

本文以机场罐式加油车为研究对象，以下简称加油车。机场无机井停机位在某个时间段内停有数架航班等待进行加油服务，现机场停有不同型号、不同数量的加油车，地面加油服务相关部门根据某一时段内机场所有降落航班的需油量指派加油车进行加油服务，所有被指派的加油车油量能充分满足该时段所有待加油服务航班的需油量。加油车在机场加油站注满油后驶向停机位为航班加油，完成一个航班的加油服务后，加油车再开往下一个停机位为另一架航班进行加油服务，直到该加油车所剩的油量不能满足其余还未加油航班的需油量。针对加油车在油罐容量有限的条件下对所有航班进行加油服务，使得加油车在有效成本范围内加油效率最大化且航班等待加油服务时间最小化，因此，本文以航班最小化完成所有航班加油服务时间为第一个目标，以所有航班等待加油时间最小为第二个目标。其中假设：(1)加油车匀速行驶；(2)加油车注油时间不计；(3)停机位之间的距离小于停机位到加油站的距离。

2.2 模型构建

指标集：

i,j：航班及补油站指标；

k：加油车型号指标；

l：加油车编号指标；

参数：

N：航班及加油站集合，即N={0,1,…,n}；

K：加油车型号集合，即K={0,1,…,k}；

L：加油车编号集合，即L={0,1,…,l}；

ti：航班i的加油时间；

Qi：航班i的需油量；

Vkl：k型号l编号加油车的油罐容量；

ri：航班i的到达时间；

aij：加油车从航班i所在停机位到航班j所在停机位的行驶时间；

a0i：加油车从加油站到航班i所在停机位的行驶时间；

M：一个非常大的整数，用于辅助建模；

决策变量：

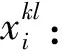
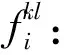
si：航班i的实际开始加油服务时间；

基于上述参数和变量的定义，机场加油车调度优化模型建立如下，其中，i或j为0表示机场加油站：

(1)

(2)

{i≠j}∈N，k∈K,l∈L

(3)

{i≠j}∈N，k∈K,l∈L

(4)

{i≠j}∈N，k∈K,l∈L

(5)

(6)

(7)

{i≠j},∈N，k∈K,l∈L

(8)

{i≠j},∈N，k∈K,l∈L

(9)

(10)

(11)

(12)

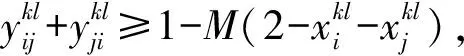
{i≠j}∈N，k∈K,l∈L

(13)

(14)

si≥ri,i∈N

(15)

(16)

(17)

(18)

(19)

(20)

(21)

目标函数(1)表示最小化所有航班加油服务完成时间；目标函数(2)表示最小化所有航班等待加油服务时间；约束(3)表示被同一辆加油车服务的两架航班，后续航班的加油开始时间不晚于前面航班的加油完成时间；约束(4)和(5)表示航班被某辆加油车服务的顺序；约束(6)和(7)表示航班没有被某加油车服务时其顺序号为0；约束(8)和(9)表示两架航班都被同一辆加油车服务且是紧邻先后关系时其加油顺序也是紧邻；约束(10)和(11)表示所有加油车都是从机场加油站出发进行加油服务；约束(12)和(13)表示加油车服务两个航班一定存在先后顺序；约束(14)表示所有航班紧邻的先后顺序之和等于加油航班数；约束(15)表示航班实际加油时间不晚于航班到达时间；约束(16)、(17)和(18)表示航班被加油车服务与两架航班被同一辆加油车先后服务和紧邻服务之间的关系；约束(19)表示被某辆加油车服务的所有航班总需油量不大于该辆加油车的油罐容量；约束(20)和(21)表示决策变量的取值范围。

3 Epsilon约束算法设计

为了精确求解该双目标优化问题，即获得最优Pareto前沿，本文使用Epsilon约束算法对所建立的双目标模型进行优化求解。Epsilon约束算法是求解多目标优化最为常用的精确算法。为了说明该精确求解双目标所使用的epsilon约束算法，首先介绍Pareto占优概念。对于最小化双目标函数而言，Pareto占优关系(<2)可以定义为：如果说一个可行解X占优于另一个可行解Y(其中X，Y为向量)，那么一定有f1(X)≤ f1(Y)和f2(X)≤ f2(Y)并且要求至少一个不等式取为严格小于号。在目标函数可行解空间里所有未被占优的点构成了Pareto前沿(Pareto Front)。在这个前沿上，任意两个点间不存在占优关系。这个解集包含了一系列不同的点(每个点为一个二元组)，这些点用于决策者进行双目标函数值间的权衡。Epsilon约束法的思想是通过转化一个目标为约束，构建并求解一系列epsilon约束问题。这一系列epsilon约束问题间是通过逐步减少的epsilon值来联系起来的(请参看Berube等[10])。为了描述epsilon约束法，还需要定义下面三类点：

由于我们建立的双目标模型中两个目标都是最小化并且目标函数值都为整数，epsilon约束算法可以表达如下。

精确epsilon约束算法：

步骤4：通过从集合F’中移除被占优的点，得到Pareto前沿F。

4 算例分析和结论

4.1 算例分析

为验证模型的可行性和求解算法的高效性，设计如下算例。假设机场在某一时段内有10架航班停在无机井的停机位等待加油服务，我们以1分钟为一个最小时间单位。利用Matlab 2014编写epsilon约束算法(调用CPLEX12.6求解单一epsilon问题)在个人电脑(i5CPU，3.0GHz处理器)上进行精确求解。

本文按照图1的机场航班所在停机位坐标信息进行仿真实验，表1是机场加油站和航班所在停机位对应的坐标位置，表格中的单位为km。例如在表1中，标号0是机场加油站，在图1中也可以找到对应加油站的位置。

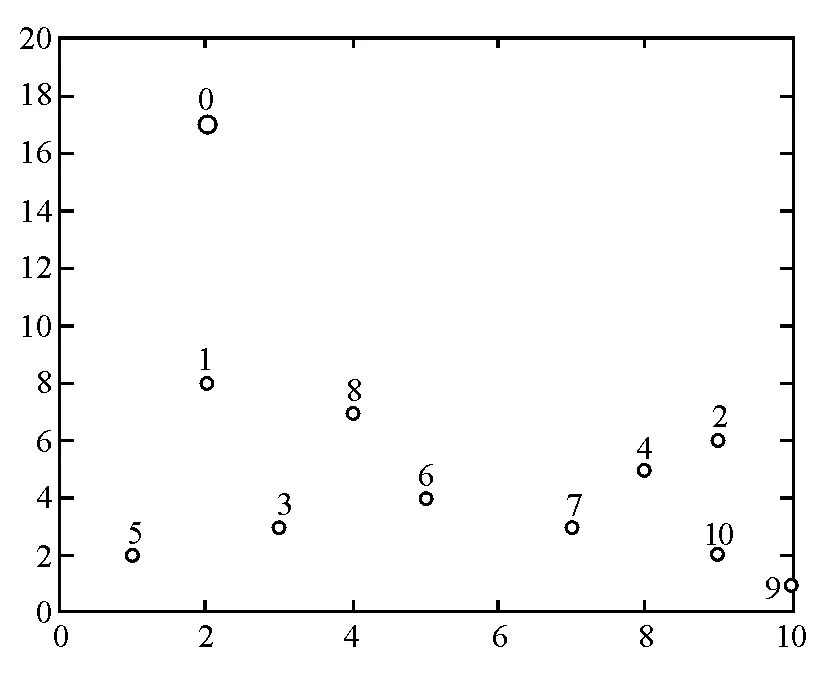
图1 仿真实验中加油站和停机位的坐标

表1 机场加油站和停机位坐标

算例的其他输入信息包含如下内容：机场地面加油服务部门指派两种型号的三辆罐式加油车进行航班加油服务，机场目前一个时段内有10架航班等待进行加油服务。航班的信息，即加油车从机场加油站到每架航班所在停机位的行驶时间h(加油车匀速行驶速度为30 km/h)，加油车从一架航班所在停机位到达另一架航班所在停机位的行驶时间a(加油车匀速行驶速度为30 km/h)，每架航班加油服务时间t，每架航班的需油量Q，每架航班的到达时间r，每辆罐式加油车的油罐容量V，随机生成如下：

t：[21 25 25 21 21 23 27 23 25 21]，

Q：[15000 1700 17000 15000 15000 16000 18000 16000 17000 15000]，

r：[39 58 24 72 11 57 39 49 19 24]，

V：[55000 55000 60000]，

h：[18 26 28 26 30 26 30 20 36 34]，

经过不到3分钟的计算时间，在个人电脑上计算求得最优Pareto前沿解集。如图2所示，其中横轴表示目标函数1的取值，纵轴表示目标函数2的取值(最小时间单位均为1分钟)。从图2中可知，当航班等待加油服务总时间最少为304个时间单位时，加油车完成所有航班的加油服务时间为384个时间单位。以此类推，当航班等待加油服务总时间为471个时间单位时，加油车完成所有航班的加油服务时间最少为356个时间单位，图2中所有星号表示最优Pareto前沿上的点。

图2 最优Pareto前沿解

4.2 结论

本文通过对航班在机场过站期间加油车服务的调度优化问题进行研究，以最小化完成所有航班加油服务时间和最小化所有航班等待加油时间为优化的双目标，利用数学规划理论建立整数规划模型，并通过epsilon约束算法精确求解算例。本文提出的模型和求解方法虽有助于帮助机场地面服务保障部门优化其设备资源提高航班的服务质量，但是如果机场可用罐式加油车数量有限，待加油服务的航班数量多，此时的调度优化问题会变得复杂。如何解决该种情况下加油车服务的调度优化，是今后进一步的研究方向。

[ 1 ] CHEUNG A, IP W H, LU D, et al. An aircraft service scheduling model using genetic algorithms[J]. Journal of Manufacturing Technology Management, 2005, 16(1): 109 -119.

[ 2 ] 王博涛. 基于遗传与启发算法的站坪调度系统应用研究[D]. 西安:西北工业大学,2006.

[ 3 ] 郑洁，高剑明. 机场地面作业调度问题研究[J]. 河北北方学院学报(自然科学版)，2008,24(6):60-62.

[ 4 ] XING Z，LIAN G. Cooperative game theoretical research for aircraft deicing operation scheduling[C]. Intelligent Control and Automation. IEEE,2012:2407-2411.

[ 5 ] NORIN A, VARBRAND P. Scheduling de-icing vehicles within airport logistics: a heuristic algorithm and performance evaluation[J]. Journal of the Operational Research Society,2012,63(8):1116-1125.

[ 6 ] 杨文东，陶婧婧，贾玉平. 机坪摆渡车实时调度系统仿真[J].南京航空航天大学学报，2013，45(6):854-858.

[ 7 ] 黄鹂诗. 基于SIMIO的机坪车辆调度仿真研究[D]. 南京：南京航空航天大学，2013.

[ 8 ] Du J Y, BRUNNER J O, KOLISCH R,Planning towing processes at airports more efficiently[J].Transportation Research Part E: Logistics and Transportation Review, 2014, 70(1):293-304.

[ 9 ] 冯霞，任子云. 基于遗传算法的加油车和摆渡车协同调度研究[J]. 交通运输系统工程与信息，2016(2):155-163.

[10] BERUBE J F, GENDREAU M, Potvin J Y. An exact ε-constraint method for bi-objective combinatorial optimization problems: application to the traveling salesman problem with profits[J]. European Journal of Operational Research, 2009,194(1): 39-50.