车用动力锂电池产热特性分析与优化

金 标，姜 斌，刘方方，姜炳春



车用动力锂电池产热特性分析与优化

金 标1，姜 斌2，刘方方1，姜炳春1

（1广东科技学院机电工程系，广东 东莞 523000；2东莞塔菲尔新能源科技有限公司，广东 东莞 523795）

为研究各散热因素对单体动力锂电池散热综合能力的影响，建立了电池三维瞬态产热数学模型，利用有限元法模拟仿真了充电工况下电池温度场分布并进行了实验验证，同时基于有限元仿真热模型及温度仿真结果采用正交实验法对电池表面散热能力的各影响因素重要度进行了计算分析，得到了最佳影响因素组合，并进行了数值仿真验证。结果表明了有限元仿真热模型可信。充电电流重要度(0.54)＞环境温度重要度(0.21)＞对流换热系数重要度(0.15)＞热辐射系数重要度(0.05)对电池散热的影响程度。优化后的电池散热性能比优化前得到提高。虚拟正交实验法在电池散热方案设计中具有实际应用价值。

产热模型；影响因素；虚拟正交实验法；方差分析

动力锂电池在频繁充放电过程中内部将产生大量热量，若散热速率远低于产热速率，将导致局部温度迅速升高，严重时造成电池热泛滥事故，因此，研究锂电池散热对解决其热安全问题具有重要意义。国内外关于锂电池散热方面的研究主要集中在其产热机理、产热模型以及各种散热影响因素分析。SATO等[1]从热力学角度讨论了锂电池的热效应并阐明其放热机理。KIM等[2]等建立了锂电池三维产热模型及电热耦合模型，并通过数值仿真法获得电池内部温度场分布。TAHERI等[3]等考虑了对流换热、热辐射边界条件以及电池内核材料具有正交特性的导热系数来研究电池热行为。JEON等[4]等模拟分析了电池在不同充放电倍率情况下的温度场。国内的匡勇等[5]等阐述了锂电池产热基本原理并总结了锂电池各种产热模型。王宇晖等[6]、罗庆凯等[7]、李争等[8]、雷治国等[9]等定性定量地分析了散热条件如环境温度、电流大小、放电速率对电池散热的影响。以上这些研究表明锂电池散热与各种因素有关，但均未定量地明确这些因素对电池散热的影响程度。本文考虑动力锂电池不同散热影响因素，利用有限元产热仿真模型进行温度场仿真分析，采用虚拟正交实验法对影响评价指标的各因素重要度进行分析，以此获得散热参数的最佳组合，保证较好的散热效果。

1 电池产热数学模型

所研究的45方形动力锂电池的外形几何尺寸参数：135 m×25 m×168 m，极柱直径和高：18 mm和10 mm;外壳厚度：1.5 mm。简化后的锂电池几何模型如图1所示，图中，线-为中心截面方向上的中心线。

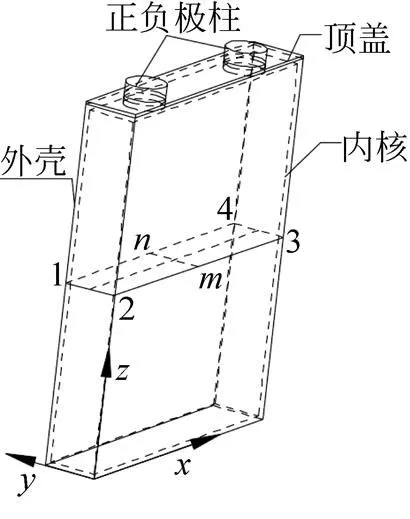
图1 简化后的锂电池几何模型

根据锂电池产热、传热及散热规律和能量守恒方程，直角坐标系下方形锂电池瞬态产热数学模 型为：

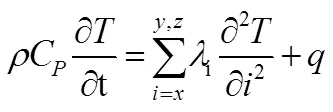
式(1)等号左侧为单位时间内电池热力学能的增量，右侧第一项为因电池表面传热而使电池在单位时间内增加的能量，第二项为电池各种产热速率的总和。式中，为电池平均密度；C为平均比热容；为时间；λ为导热系数，下标、、代表坐标；为产热速率，由电池内核及极柱两部分的产热速率组成，可分别根据BERNADI等[10]提出的经典公式及焦耳热公式进行计算。对于电池表面与外界之间的边界条件如对流换热系数、热辐射系数可通过ANSYS有限元软件进行设置。式中关于电池内核材料的三维正交导热系数可利用CHEN等[11]提出的计算方法计算得到，其它材料如铝、铜可通过手册查询得到。锂电池热仿真所需的材料属性如表1所示。

表1 锂电池热仿真所需的物性参数

2 温度场模拟结果与讨论

利用上述产热数学模型以及ANSYS有限元分析软件，对以下4种典型工况进行模拟：①环境温度0=298 K，对流传热系数=5 W·m-2·K，热辐射系数ε=0.9时不同充电电流对电池热行为的影响；②充电电流=45 A，对流传热系数=5 W·m-2·K，热辐射系数=0.9时不同环境温度0对电池热行为的影响；③充电电流=45 A，环境温度0=298 K时，不同对流换热系数对电池热行为的影响； ④充电电流=45 A，环境温度0=298 K时，不同热辐射系数对电池热行为的影响。仿真时初始温度取300 K。

图2-3为电池在工况①下，电池表面温度场分布云图以及电池充电结束时不同充电电流时电池线m-n的温度分布。图4-6分别为工况②～④下，电池充电结束时，电池线m-n的温度分布曲线。

由图2可看出，充电结束后电池外壳中心温度较高，边缘温度较低。由于电池正负极极柱产热量较小，因而极柱处温度相对较低。另外，由于盖板热量来自极柱及外壳的传热，因此温度最低。从图2(c)可知：充电电流为67.5 A时，电池内部温度高达327.1 K。从图3温度分布曲线可知：曲线呈对称分布，电池内部中心温度最高，表面温度最低。从图4可知：在相同充电电流和对流换热系数条件下，环境温度越高，电池内部温度越高；环境温度从298～318 K变化范围内，电池最高温度约从315.5～331.0 K，这是因为电池表面散热依靠对流换热，而换热量与环境温度成反比，环境温度越高，电池与外界换热量越小，对流换热效果越差。从图5可看出：对流换热系数越大，电池温度越低，这是由于在环境温度一定情况下电池表面与对流换热量与对流换热系数大小成正比。从图6可看出，热辐射系数变化对电池温度有影响。热辐射系数越大，电池表面温度越低。

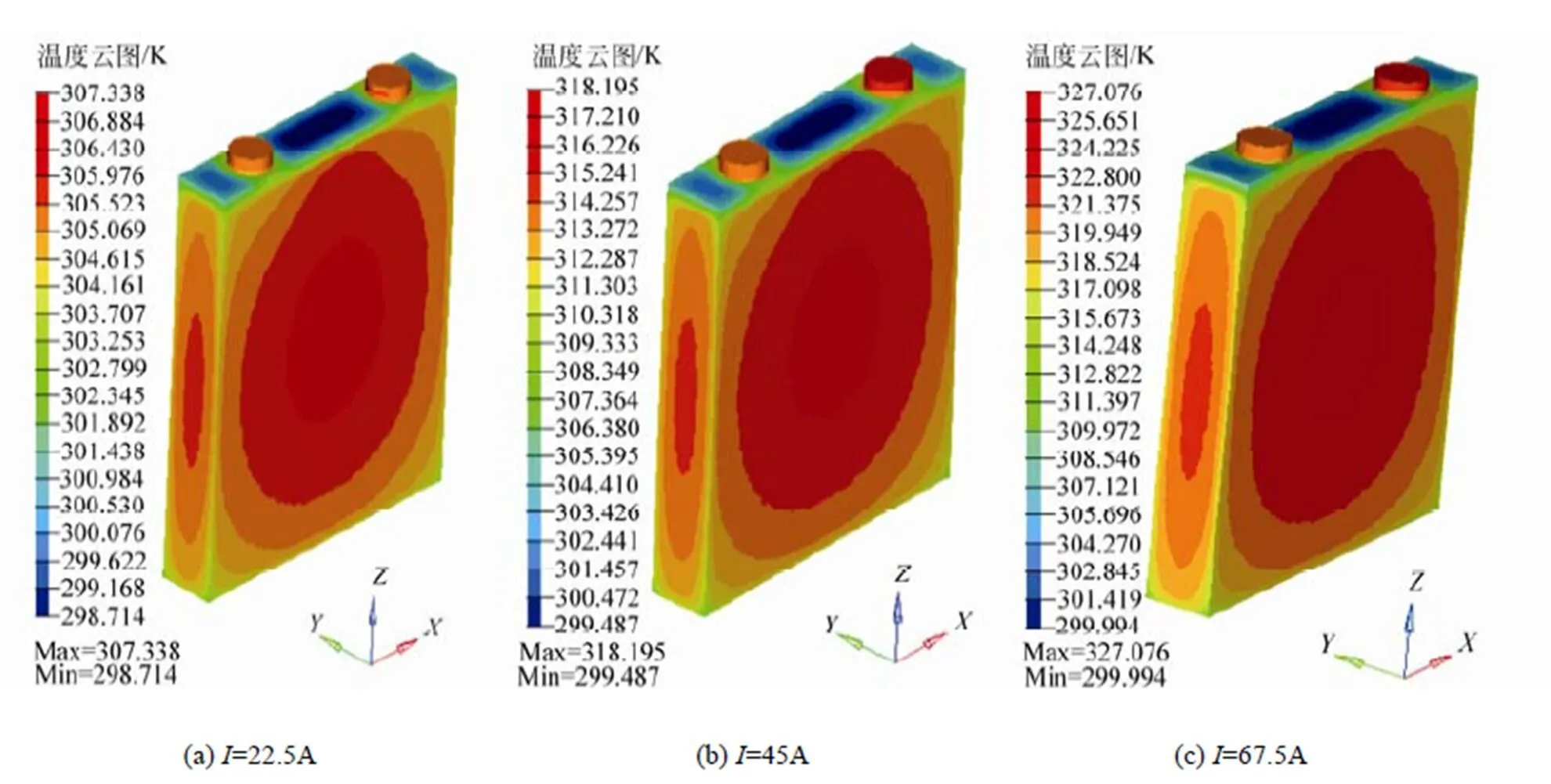
图2 工况①下不同充电电流时电池表面温度分布云图

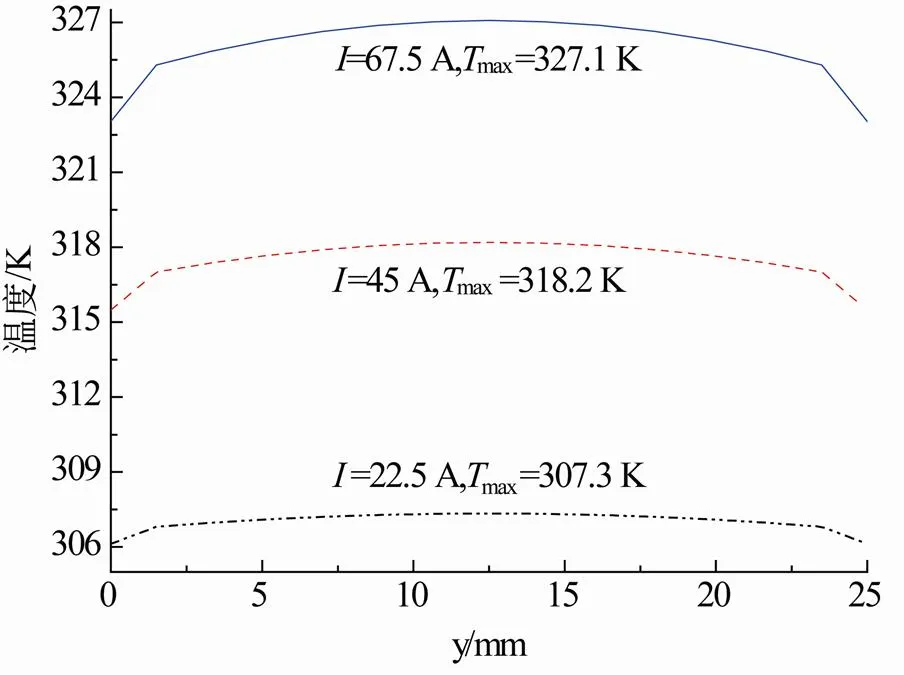
图3 工况①中不同充电电流时电池线m-n的温度分布

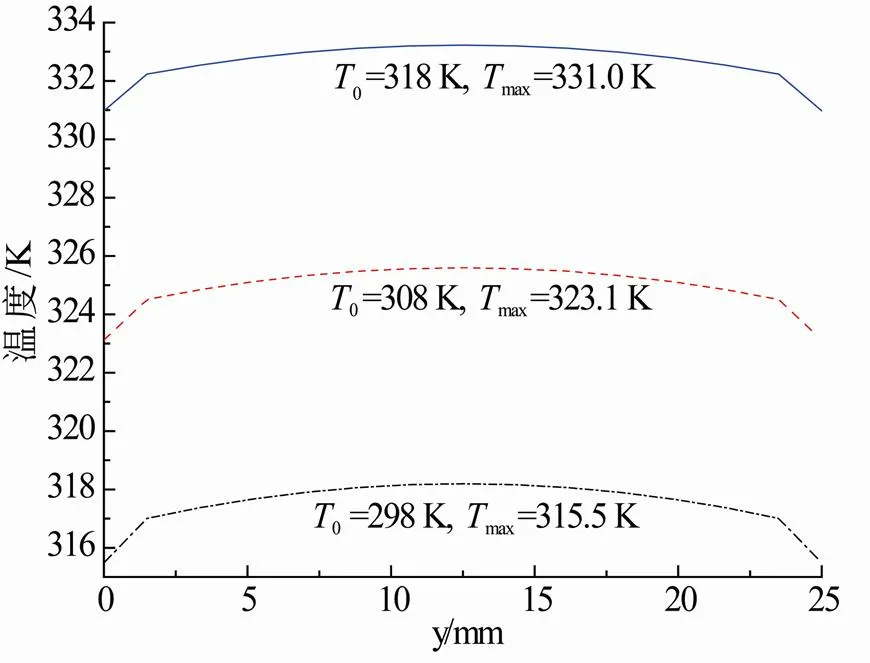
图4 工况②中不同环境温度时电池线m-n的温度分布

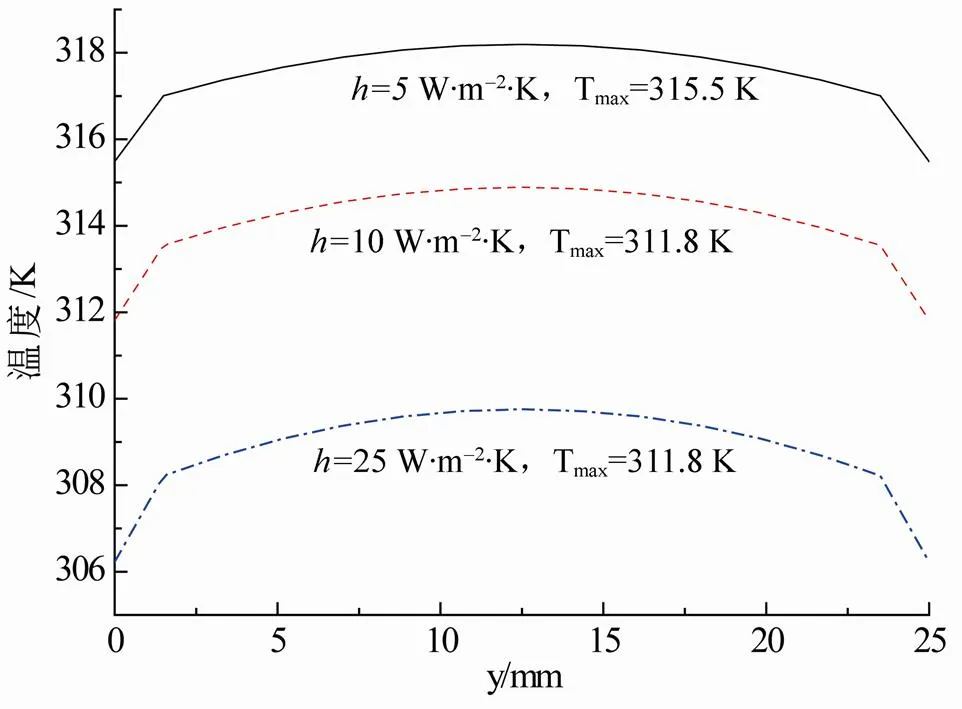
图5 工况③中不同对流换热系数下电池线m-n的温度分布

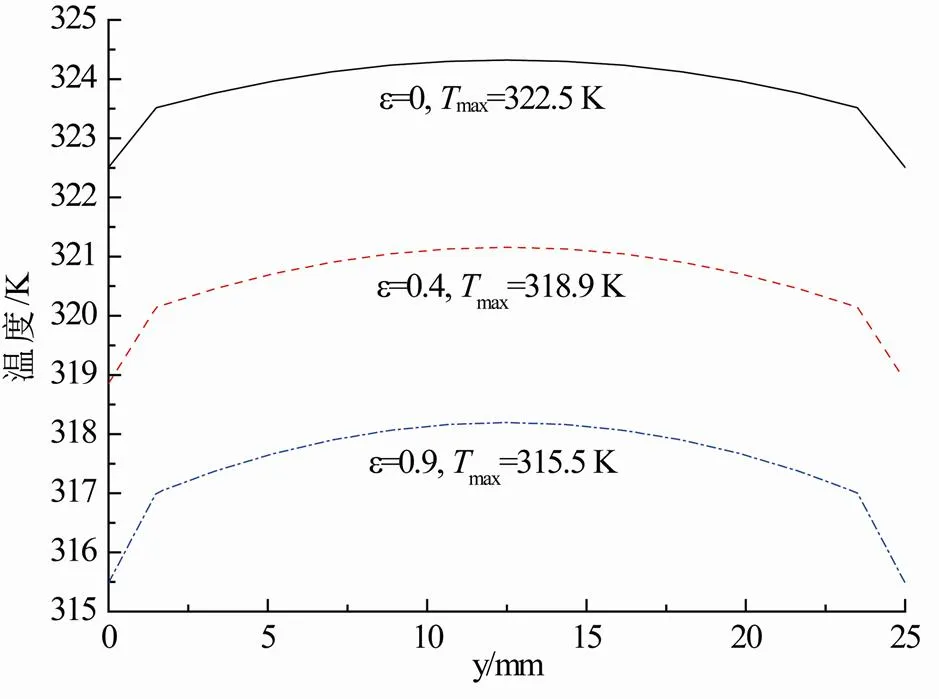
图6 工况④中不同热辐射系数下电池线m-n的温度分布

3 试验与仿真结果对比

图7为温度传感器布置点，充电试验过程中取图中5个监控点的温度平均值作为电池表面平均温度，且与仿真结果进行比较。仿真时环境温度、初始温度、辐射率和对流换热系数分别取298 K、300 K、0.9和5 W·m-2·K-1。试验与仿真结果对比曲线如图8所示。从图8可知：0.5C、1C、1.5C（C为充电倍率）充电结束后，试验得到电池表面最高温度分别为309.5 K、323.7 K、333.2 K，与仿真值相比，最大温度差分别为1.37 ℃、1.98 ℃、2.13 ℃，试验值与仿真值比较接近，温度相差在2.5 ℃以内，表明有限元仿真热模型能较好地反映出该电池在充电过程中的产热情况，证明该有限元仿真热模型的准确性。

图7 传感器布置点分布图

图8 试验与仿真结果对比曲线

4 散热影响因素重要度分析与优化仿真

从上述温度场模拟仿真可知，充电电流、环境温度、对流传热系数和热辐射系数都是影响电池表面散热的重要参数，但这些参数对电池散热影响程度还不明确。正交实验设计是一种安排多因素试验、确定各因素影响程度、寻求最佳水平组合的高效率实验设计方法，因此，对于以上不确定的电池散热影响因素，可通过设计正交试验，分析各影响因素对电池表面散热影响重要性主次顺序，并选择最优组合。

4.1 双指标虚拟正交实验设计

分别在不同充电电流、环境温度T、对流传热系数、辐射系数等工况下进行热模拟，电池表面最高温度Tsmax及表面温度均匀性作为评价电池散热性能的两个指标，定义如下：(TsmaxTsmin)(TsmaxTsmin)，Tsmin为外壳最小温度。本实验共4个实验因素，每个实验因素各取3个水平。本次实验不考虑因素间的交互作用，得到实验表头形式如表2所示。

表2 因素水平表

4.2 虚拟正交实验（DOE）

利用有限元仿真热模型，进行虚拟仿真实验，即在不同工况下对电池进行热仿真得到各因素水平下的虚拟实验指标。实验方案及结果如表3所示。

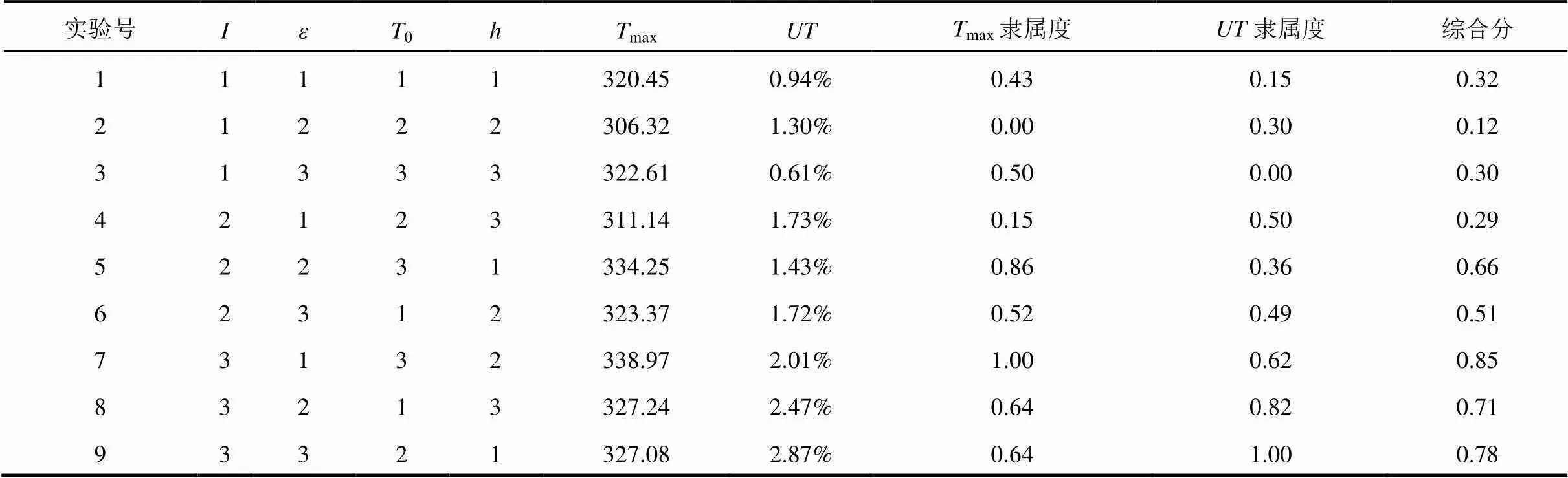
表3 不同工况电池热仿真实验方案及结果

4.3 实验结果直观分析

电池散热的综合性能取决于最高温度、散热均匀性2个指标。要得到最优试验方案，则应综合考虑这2个试验指标。对于双指标正交试验优化问题，本文采用综合评分法得到最优方案。

（1）按式（2）计算每号实验结果的每个指标的隶属度。

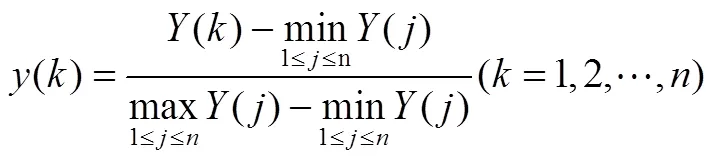
其中，表示每号实验结果值，表示实验数。

（2）给出各指标相对重要性权数。本文最高温度权重取0.6，温度均匀性权重取0.4，并按式（3）作为该号实验总分数。

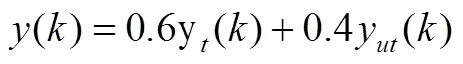
其中，y()、y()分别表示最高温度及温度均匀性指标的隶属度。实验总分数越小，表明电池散热综合性能越好。

（3）正交实验结果方差分析

计算综合指标实验结果的总和、均值和极差。实验结果总和K为第个实验因素的第个水平实验结果之和。实验结果均值k表示第个实验因素的第个水平实验结果之和与各水平的实验次数的比值。极差R为实验因素各水平的实验结果平均值的最大值与最小值的差值，即

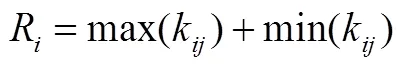
极差大小反映了相应实验因素对实验结果重要性的大小。极差值越大，反映该因素的变化对实验结果的影响越大，因素越重要。实验结果总和、均值及极差计算结果如表4所示。

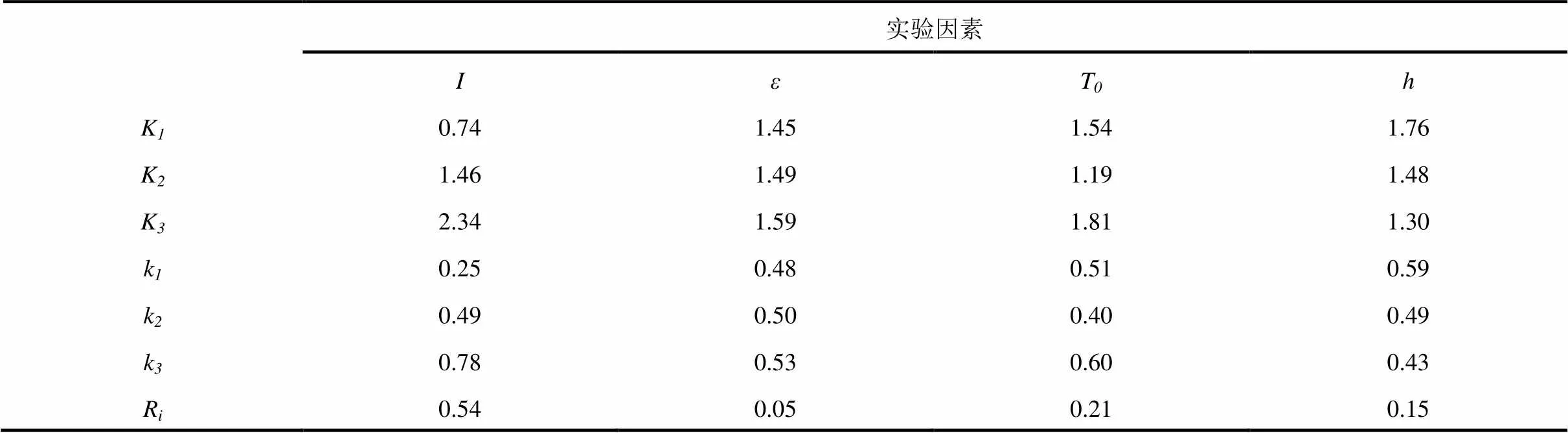
表4 实验结果总和、均值及极差计算结果

从表4可知，根据计算的极差值大小可得到散热影响因素的主次顺序：>T>>。从产热数学公式可知，在充电过程中，充电电流是内部产热的直接原因，因此，它对电池表面散热影响程度最大，其重要度为0.54。从对流换热原理可知，对流换热可通过降低环境温度来降低电池外部温度即环境温度，所以，环境温度和对流换热对电池表面散热的影响相当，重要度分别为0.21和0.15。热辐射对电池表面散热的影响最小，重要度为0.05。

4.4 趋势分析

图9为综合指标效应曲线图。图中，横坐标表示各散热因素的各水平，纵坐标表示相应因素各水平的实验结果综合分数。由图可知，充电电流和环境温度0两个影响因素越大，综合分数越大，在所选水平区间内表现为单调递增的趋势；对流换热系数影响因素越大，综合分数越小，在所选水平区间内表现为单调递减的趋势；热辐射系数的趋势曲线较平缓，表明该影响因素的变化对电池综合散热指标的影响不大。

图9 综合指标效应图

4.5 双指标试验综合评分法结果分析

根据图9，22.5 A的充电电流对应的综合分最小，该影响因素为散热可控因素，即电池以0.5 C充电倍率进行慢充电。298 K的环境温度对应的综合分数最小，环境温度越低，消耗的汽车空调的能量越多；5 W·m-2·K-1的对流换热系数对应的综合分数最小，但考虑到散热装置耗能问题，充电过程中取10 W·m-2·K-1（一般强度强制风冷散热方式）即可；热辐射系数取0时的综合分数最低，但目前动力锂电池外壳一般为铝壳，一般对铝壳进行了工艺处理，考虑成本因素，铝壳表面热辐射系数可取0.4。由以上分析得出，最优组合影响组合方案可为1（22.5 A）、3（0.4）、02（298 K）、1（10 W·m-2·K-1），即对应表3中的第2种工况。而锂电池实际使用条件大多数是1 C倍率充电、铝壳表面氧化抛光处理、室温下、一般自然对流，因此实际影响因素组合是2（45 A）、3（0.9）、02（298 K）、1（5 W·m-2·K-1）。

4.6 仿真验证

优化前方案即实际影响因素组合方案和优化后方案即最优影响因素组合方案未出现在表3工况中，对优化前后方案进行温度场仿真计算，得到优化前后该单体动力电池表面的温度分布，如图10所示。由图可知：优化前电池较优化后电池表面温度梯度较明显，即优化后电池表面分布较均匀，优化前后的最高温度分别为313.3 K、305.8 K。根据仿真结果以及正交试验直观分析计算可得到优化前后仿真优化结果对比见表5，从表中可看出，优化后方案电池综合分较优化前降低了70.4%，表明优化后方案电池的散热综合性能得到提高。

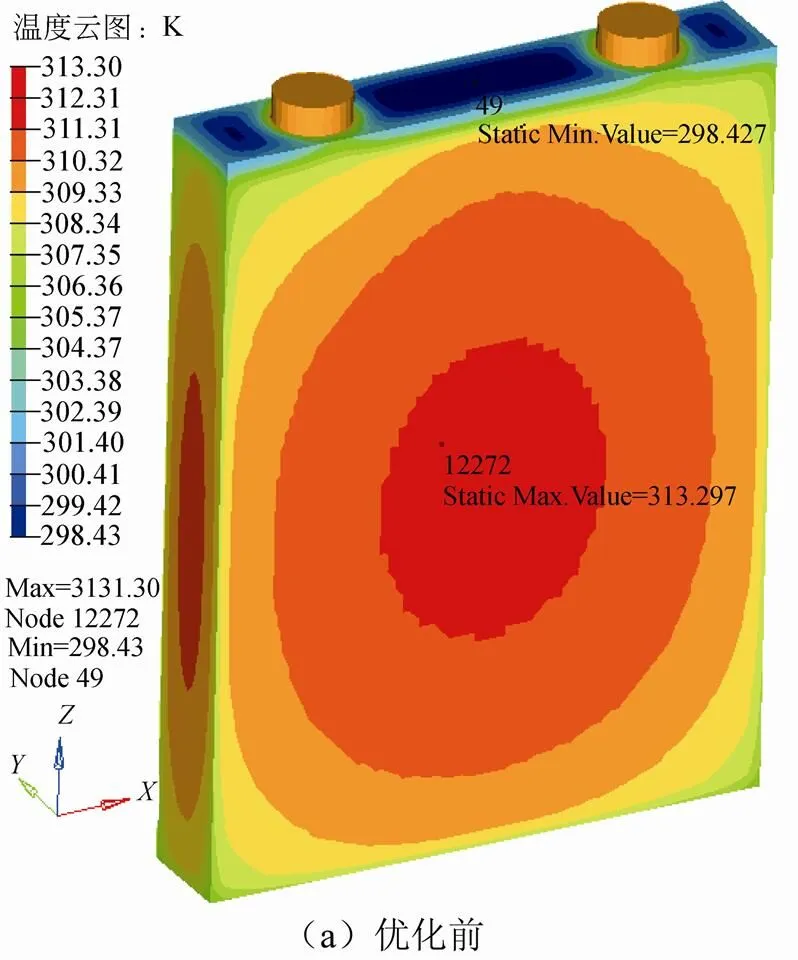
表5 优化前后设计结果对比

5 结 论

通过多工况下锂电池的温度场仿真及基于虚拟正交实验的散热影响因素的重要度分析可知：影响电池散热综合性能指标的最重要因素是充电电流，环境温度和对流换热系数依次次之，热辐射系数对其结果影响最小。考虑耗能、成本等因素，最优影响因素组合为1（22.5 A）、2（0.4）、02（298 K）、2（10 W·m-2·K-1），通过优化前后的有限元仿真对比结果可知，优化后的电池散热综合性能比优化前有所提高，表明虚拟正交实验方法在电池散热方案设计中的应用前景。

[1] SATO N, YAGI K. Thermal behavior analysis of nickel metal hydride batteries vehicles[J]. JSAE Review, 2000, 21(2): 205-211．

[2] KIM G H, SMITH K, PESARAN A. Lithium-ion battery safety study using multi-physics internal short-circuit model[R]. CA: NREL, 2009．

[3] TAHERI P, YAZDANPOUR M, BAHRAMI M. Transient three-dimensional thermal model for batteries with thin electrodes[J]. Journal of Power Sources, 2013, 243(243): 280-289．

[4] JEON D H. Numerical modeling of lithium ion battery for predicting thermal behavior in a cylindrical cell[J]. Current Applied Physics, 2014, 14(2): 196-205．

[5] 匡勇,刘霞,钱振,等. 锂离子电池产热特性理论模型研究进展[J]. 储能科学与技术,2015,4(6): 599-608．

KUANG Yong, LIU Xia, QIAN Zhen, et al. Review on heat generation theory model of lithium-ion battery[J]. Energy Storage Science and Technology,2015,4(6): 599-608．

[6] 王宇晖, 靳俊, 郭战胜, 等. 锂硫电池放电过程的热模拟[J].储能科学与技术,2017,6(1): 85-93．

WANG Yuhui, JIN Jun, GUO Zhansheng, et al. Thermal simulation for lithium-sulfur battery during discharge process[J]. Energy Storage Science and Technology,2017, 6(1): 85-93．

[7] 罗庆凯, 王志荣, 刘婧婧,等. 18650型锂离子电池热失控影响因素[J].电源技术, 2016, 40(2): 277-376．

LUO Qingkai, WANG Zhirong, LIU Jingjing, et al. Influencing factors of thermal runaway of 18650 lithium ion battery[J]. Chinese Journal of Power Sources, 2016, 40(2): 277-376．

[8] 李争, 邢殿辉. 基于有限元分析的动力锂离子电池生热特性研究[J]. 湖南科技大学学报, 2016, 31(1): 42-48．

LI Zheng, XING Dianhui. Thermal performance characteristics of lithium-ion power battery based on finite element analysis[J]. Journal of Hunan University of Science ＆ Technology, 2016, 31(1): 42-48．

[9] 雷治国, 张承宁, 雷学国, 等. 电动汽车用锂离子电池热特性和热模型研究[J]. 电工电能新技术, 2015, 34(12): 59-64．

LEI Zhiguo, ZHANG Chengning, LEI Xueguo, et al. Research on thermal characteristics and thermal model of EVs lithium-ion battery[J]. Advanced Technology of Electrical Engineering and Energy, 2015, 34(12): 59-64．

[10] BERNADI D, PAWLIKOWSIKI E, NEWMAN J T. A general energy balance for battery system[J]. J. Electrochem. Soc., 1985, 132(1): 5-12．

CHEN S C, WAN C C, WANG Y Y. Thermal analysis of lithium-ion batteries[J]. Journal of Power Sources, 2005, 140(1): 114-115．

Thermal characteristic analysis and optimization for vehicle power lithium battery

JIN Biao1，JIANG Bin2，LIU Fangfang1，JIANG Bingchun1

(1Department of Mechanical and Electrical Engineering,Guangdong University of Science & Technology,Dongguan 523000, Guangdong, China；2Dongguan TAFEL New Energy Technology Co., LTD, Dongguan 523795，Guangdong，China)

To investigate the influence of heat dissipation factors on the comprehensive cooling capability for the rectangle power lithium battery, a three-dimensional transient thermal mathematical model was established under different operating conditions during charging process, making use of which the battery temperature field distribution was simulated at different charging current, ambient temperature, convective heat transfer coefficient and thermal emissivity based on the finite element method. In the meantime, the simulation results were verified experimentally, according to the results obtained by verified finite element thermal model, using the virtual orthogonal experiment method, the importance degree of influence factors was calculated and analyzed. The optimum combination of influence factors was attained, and the temperature field distribution of the original scheme(practical influence factors) and the optimized scheme(the optimum influence factors) was simulated using finite element thermal model. The results show that the thermal model of finite element is credible, and the most significant factor on the battery comprehensive cooling capacity is the charging current, whose important degree is 0.53, while the important degree of the ambient temperature is 0.21, the important degree of the convective heat transfer coefficient is 0.15, and the important degree of the thermal emissivity is 0.05, playing the least important part in the battery heat dissipation. In conclusion, the battery comprehensive cooling performance after optimization is better than that before optimization, and the virtual orthogonal experiment method has certain value of practical application in battery cooling scheme design and optimization.

heat production model；influence factor；virtual orthogonal experimental method；variance analysis

TM911.41

A

2095-4239（2018）01-128-07

10.12028/j.issn.2095-4239.2017.0140

2017-08-14；

2017-09-30。

广东省青年创新人才类项目（2015KQNCX190，2016KQNCX 189）；东莞市社会科技发展项目（2017507154411）。

金标（1981—），男，硕士研究生，讲师，主要研究方向：动力锂电池热管理及优化，E-mail：53340450@qq.com。