基于SVM和遗传算法的装甲车齿轮箱故障模式识别

周昕晨，林 董，汪栋洋

(中国人民解放军陆军步兵学院(石家庄校区)，河北 石家庄 050000)

随着人工智能技术的发展，专家系统虽被广泛地应用到故障诊断领域中，但是仍存在知识获取困难等问题。20世纪90年代，神经网络方法日趋成熟，但是存在泛化能力差、小样本处理能力较弱等缺点。在神经网络的发展遇到问题时，一种新的机器学习方法应运而生，即支持向量机(Support Vector Machine, SVM)[1-2]。SVM是基于小样本统计理论的学习方法，它突破了传统的经验风险最小化原则，追求的是结构风险最小化，所以泛化能力很强，有效地解决了小样本问题[3]。SVM在解决非线性问题上运用了核函数方法，克服了神经网络等方法中运算速度慢、容易陷入局部极小值的缺点。

因为SVM中参数选择对分类性能有较大影响，所以，越来越多的人对SVM的参数选择进行研究，如李娇对支持向量机参数优化进行了研究，采用了遗传算法和粒子群算法进行参数优化研究，避免因参数选择不当而导致效果不理想[4]；尹子任等在支持向量机的输电线路覆冰预测中引入了粒子群算法进行优化[5]；陈伟根等对变压器的绕组热点温度支持向量机的预测模型引入了遗传算法进行参数优化[6]；朱伟等在再生混凝土抗压强度的支持向量机预测模型中进行了遗传算法参数优化，提高了预测精度[7]；袁玉萍等研究了遗传算法在支持向量机模型中的参数优化，并用算例进行了验证，证明了经过优化后的分类精度和效率得到了提高[8]。

由于现有研究中参数选择困难的问题尚未得到很好的解决，致使故障诊断准确度不高。本文提出一种基于遗传算法的参数优化方法，并对试验信号和工程信号进行了参数优化前后的性能对比，结果表明，经过参数优化后诊断精度得到了提高。

1 支持向量机

1.1 线性支持向量机

以二维线性可分的分类问题(见图1)为例。设数据集T={(xi，yi)|i=1，2，…，n}，其中：xi∈Rn，yi∈(-1，+1)，假设存在判别函数：

f(x)=sgn(w·x+b)

(1)

由于yi∈(-1，+1)，所以要使得所有数据点到最优分类线的距离都>1，即：

yi(wixi+b)-1≥0

(2)

图1 线性可分的分类问题

由图1可以看出，w·x+b=0是区分样本的超平面，为了使分类平面将2类样本最大限度的区分，则需要分类间隔最大化，可以转化为约束优化问题：

(3)

s.t.yi(w·x+b-1)≥0

(4)

该约束可以通过构造Lagrange函数求解：

(5)

式中，αi为Lagrange乘子，αi≥0。

对Lagrange函数求w和b的偏导，根据优化条件得：

(6)

根据上式结果得：

(7)

求出构造超平面的参数，则分类判别函数为：

f(x)=sgn(∑yiaixix+b)

(8)

根据f(x)的值就可以判断x的类别。

1.2 非线性支持向量机

当存在一些不可以线性可分的点时，则在约束条件下引入松弛变量ξi≥0，即：

(9)

s.t.yi(w·x+b)≥1-ξi

(10)

为了构造Lagrange函数，引入了Lagrange乘子，求解得：

(11)

(12)

对上式求解得：

(13)

(14)

判别函数：

f(x)=sgn(∑yiaixix+b)

(15)

现实情况中存在更多的是非线性的情况，所以在对非线性数据集进行分类处理时，就需要将样本特征通过映射函数φ(x)映射到高维空间(见图2)。则优化问题变为：

(16)

(17)

设K(xi,xj)=φ(xi)φ(xj)，则上式简化为：

(18)

(19)

判别函数为：

(20)

式中，K(xi,xj)称为核函数。

图2 输入空间到特征空间的映射

常用的核函数如下。

1)高斯径向基核函数：

(21)

2)多项式核函数：

K(xi,xj)=(xixj+1)d

(22)

3)Sigmoid核函数：

K(xi,xj)=tan[k(xixj)+v]

(23)

式中，σ、ν为核函数系数。

SVM的参数选择对性能影响很大，需要确定的参数为惩罚参数C和核函数系数σ。C和σ的取值不同则模型的性能不同。针对不同的模型参数取值没有一定的理论参考，如果对参数的取值采用尝试的方法，这样的工作量极大，效率低下。

SVM模型训练结果如图3和图4所示。图3中C，σ初始值为(5，0.1)时，分类正确率为77%；图4中C，σ初始值为(10，0.5)时，分类正确率为83%。由此可以看出，在参数选择合适初始值的情况下，SVM才能实现很好的分类，参数选择的不同将会有不同的分类效果。

图3 SVM模型训练结果1

图4 SVM模型训练结果2

由于遗传算法具有隐含的并行性和较好的全局搜索能力等优点，可以在较短的时间内搜索到全局最优点[9]，所以针对齿轮箱故障诊断模型为了选择最佳的参数，本文选择了遗传算法对齿轮箱支持向量机故障诊断模型进行参数优化。

2 遗传算法

2.1 遗传算法基本思想

遗传算法(Genetic Algorithm，GA)是工程科学和生命科学相互交叉的产物，是一种通过借鉴生物界的进化规律发展的高效全局优化搜索算法，经过选择、遗传和变异等操作，提高各个体的适应性[10]。遗传算法不基于具体问题，强大的随机搜索能力和天然的并行性使其广泛应用在机器学习、模式识别等领域[11]。遗传算法[12-13]通过对种群进行基因编码，按照适者生存方式，选择出适应度最好的个体，借用自然遗传学中的遗传操作进行组合交叉和变异操作产生出新的种群，使得新总群具有更好的适应性。

2.2 适应函数

遗传算法把问题空间映射到染色体位串空间，为了适者生存的原则，必须对个体的染色体位串的适应度进行评价，所以，适应函数组成了个体的生存环境。此次选择训练好的SVM分类器计算测试样本数据的识别率为适应度函数，以此来判断是否满足停止准则。首先，对支持向量机分类模型中的主要参数即惩罚因子和核函数值进行编码操作并随机生成初始化种群；然后，对种群的各个染色体进行解码，获取出适应值较好的惩罚因子和核函数值，并用选择出的参数值用样本数据集训练分类器模型，用训练好的分类器模型对测试集进行测试。识别率计算式如下：

(24)

式中，s为测试样本中分类争取的样本数目；t为测试样本的总数目。

由于识别率在一定程度上反应了分类模型的推广能力和分类能力，所以根据识别率来构造适应度函数，即：

Fitness=RR

(25)

3 基于GA的齿轮箱SVM模型的参数优化

SVM的2个参数C和σ对齿轮箱模型分类识别性能有很大的影响，为了提高分类识别性能，选择GA对参数进行优化。

3.1 样本选择与处理

实验台轴承为6307轴承，一个为正常轴承，另一个为外圈点蚀的轴承。采集数据后进行数据处理，提取时域特征与小波包节点能量，由于各指标数值的范围有所差别，在进行特征选择之前先进行归一化处理，归一化到[0，1]，然后应用Fisher准则进行特征选择。选择裕度指标与峭度指标作为支持向量机数据样本特征向量。采集160组正常及故障状态下的数据，其中80组作为训练样本，80组作为测试样本。选用径向基核函数作为支持向量机核函数，该函数有1个核函数参数σ，设σ的取值范围为0～100，C的取值范围为0～1 000。

3.2 参数优化结果分析

取GA群体规模为50，最大迭代次数为100，采用单点交叉方式，交叉概率为0.7，变异概率为0.01，终止条件为满足最大迭代次数(即100)时停止进化。经过遗传算法进行优化之后可以得到最优的参数为：核函数参数σ的最优解为84.916 9，惩罚参数C的最优解为134.1，诊断精度为95%。GA参数优化后的性能与未优化的性能对比见表1。

表1 SVM分类性能对比

未经参数优化的分类结果、遗传算法优化适应度以及经过GA参数优化之后的分类结果分别如图5～图7所示。

图5 未经参数优化的分类结果

图6 遗传算法优化适应度

图7 经过GA参数优化后的分类结果

4 工程数据分析

图8 轴承外圈故障

某装甲车齿轮箱的轴承外圈故障如图8所示。

选择发生故障时的数据和正常运转时的数据进行数据处理，根据Fisher准则，提取Fisher准则值较大的特征峭度指标和裕度指标作为SVM模型的输入，并选择出训练集和测试集，建立SVM分类模型，进行GA参数优化，比较其分类性能。

支持向量机核函数选用最常用的径向基核函数，该函数有0个核函数参数σ，设σ的取值范围为0.01～100，C的取值范围为0～100。取GA群体规模为50，最大迭代次数为100，采用单点交叉方式，交叉概率为0.6，变异概率为0.001，终止条件为满足最大迭代次数(即100)时停止进化。

经过遗传算法进行优化后可以得到最优的参数为：核函数参数σ的最优解为92.30，惩罚参数C的最优解为2.25，诊断精度为100%。GA参数优化后的性能与未优化的性能对比见表2。

表2 SVM分类性能对比

未经参数优化的分类结果、遗传算法优化适应度以及经过GA参数优化后的分类结果分别如图9～图11所示。

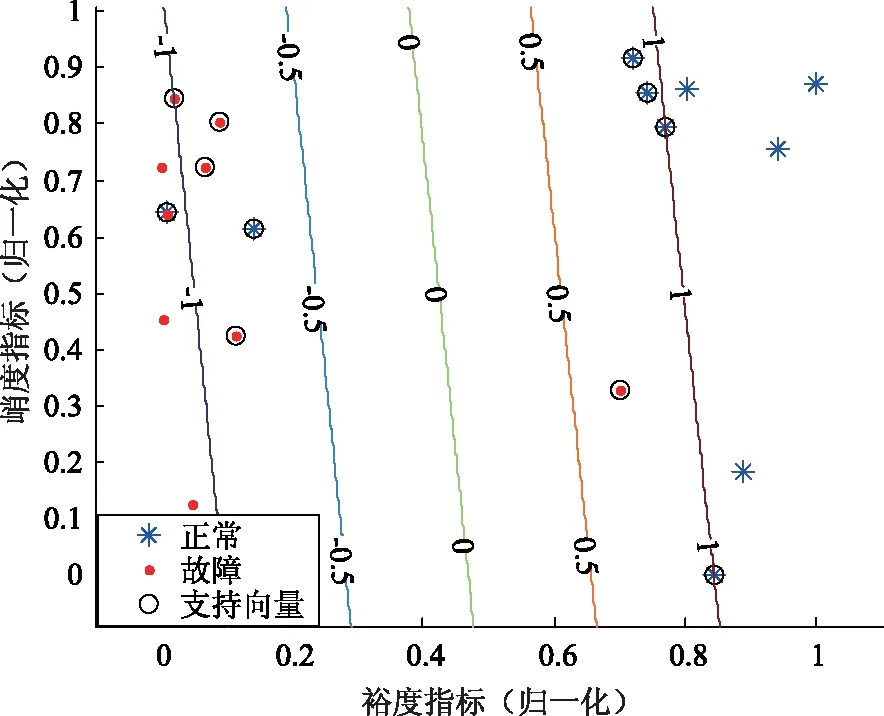
图9 未经参数优化的SVM模型分类结果

图10 遗传算法优化适应度

图11 经GA参数优化后的SVM模型分类结果

5 结语

齿轮箱SVM模型中参数的选择对模型分类性能有较大影响。在齿轮箱支持向量机模型中引入遗传算法对参数进行优化，通过未经过参数优化的SVM模型性能与经过GA参数优化后的SVM模型性能进行对比可以看出，对于二分类或者多分类来说，GA参数优化后的模型都能够有更好的分类性能。工程数据验证可以看出，经过GA参数优化后的齿轮箱SVM模型能够更好地进行模式识别，对于实现齿轮箱故障智能诊断提供了帮助。

[1] 张继强. 基于模糊专家系统的矿井提升机电控系统的故障诊断[D]. 西安：西安科技大学, 2012.

[2] Zhang B, Yin J, Wang S L, et al. Research on virus detection technique based on ensemble neural network and SVM[J]. Neurocomputing, 2014, 137:24-33.

[3] Shao Z, Zhang L, Zhou X, et al. A novel hierarchical semisupervised SVM for classification of hyperspectral images[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11:1609-1613.

[4] 李娇. 支持向量机参数优化研究[D]. 武汉: 华中师范大学，2011.

[5] 尹子任, 苏小林. 基于粒子群算法优化支持向量机的输电线路覆冰预测[J]. 电力学报, 2014, 29(1):6-9.

[6] 陈伟根, 滕黎, 刘军, 等. 基于遗传优化支持向量机的变压器绕组热点温度预测模型[J]. 电工技术学报, 2014, 29(1):44-51.

[7] 朱伟, 石超峰, 李楠. 基于遗传算法优化支持向量机的再生混凝土抗压强度预测模型[J]. 中外公路, 2014, 34(1):311-314.

[8] 袁玉萍, 胡亮, 周志坚. 基于遗传算法对支持向量机模型中参数优化[J]. 计算机工程与设计, 2008, 29(19):5016-5018.

[9] Goldberg D E. Genetic algorithms in search, optimization and machine learning[J]. MA: Addison-Wesley Publishing Company, 1989, 3:95-99.

[10] Mitchell M. An introduction to genetic algorithms[M]. Cambridge: MIT Press, 1996.

[11] De Jong K A. The analysis of the behavior of a class of genetic adaptive systems[M]. Ann Arbor: University of Michigan, 1975.

[12] Chauvin M, Lascoup B. Contribution to lightening in the automotive industry: application of the twist-beam rear axle[J]. Revue de Métallurgie, 2011, 108(7/8):427-435.

[13] Jack L B, Nandi A K. Fault detection using support vector machines and artificial neural net works augmented by genetic algorithms[J]. Mechanical Systems and Signal Processing, 2002, 16(2):373-390.