基于CFD的水平井压裂管柱有限元分析

魏新丁

(西南石油大学，四川 成都 610500)

由于水平井井眼轨迹较为复杂(包括直井段、弯曲段和水平段)，造成压裂管柱在下入过程中会与井壁产生较多的接触，增大了压裂管柱下入的摩阻力，从而增大了压裂管柱下入的难度[1]。随着压裂级数的增多，压裂管柱的设计变得更加复杂，使得管柱与井壁之间的情况也更加复杂。受管柱刚度的影响，管柱在下入的过程中会发生弯曲，并产生很大的弯曲应力，过大的弯曲应力会降低管柱的强度，甚至影响管柱在作业过程中的安全性。当管柱下入到预定位置时开始坐封和压裂作业，管柱由于受到内外压差、温度和管内流体的作用，使其受力情况变得更加复杂[2]。本文对水平井多级压裂管柱下入过程的摩阻力进行了分析，以确保管柱不会因为摩阻力过大而发生屈曲变形，并对坐封和压裂施工过程中的水平井压裂管柱进行了有限元分析，以确保水平井多级压裂管柱的作业安全性。

1 研究假设

本文以水平井压裂管柱为研究对象。为了便于研究分析，在建立分析模型时作如下假设：1)管柱与井壁的横截面为规则的圆形；2)初始状态下，管柱轴线与井眼轴线重合，管柱与井壁间存在环空间隙；3)受力变形后的管柱与井壁接触，且接触点位置不固定，接触点存在接触反力和摩擦力。

2 水平段管柱有限元分析

2.1 有限元模型的建立

水平段管柱为封隔器、压裂滑套和管柱组成的压裂工具串，A水平井的2个封隔器平均间距为80 m。水平段井眼为裸眼段，井眼直径为152.4 mm。压裂管柱外径为114.3 mm，壁厚为7.37 mm，钢级为P110，材料参数如下：弹性模量为2.06 GPa，泊松比为0.3，密度为 7 800 kg/m3，屈服强度为757.54 MPa，抗拉强度为861.42 MPa。根据上述水平段井眼的数据以及管柱的几何形状，建立的水平段压裂管柱有限元模型如图1所示。模型为80 m长的水平管内管模型，其中外管用来模拟井筒环境，内管为压裂管柱。利用LESIZE尺寸控制命令对单元尺寸进行控制，网格划分单元长度为0.1 m，周向16等分，截取的一段管柱与井眼网格划分模型如图2所示。

图1 水平段压裂管柱有限元模型

图2 管柱网格划分模型

在管柱与井壁之间建立接触，管柱在井眼内接触滑动，与上一节弯曲段管柱与井壁的接触设置相同。CONTA176用来模拟三维梁或管之间的大变形接触，包括一根管在另一根管内部滑动的管接触、相邻2根近似平行梁之间的外部接触、2根交叉梁之间的外部接触等各种形式。接触单元选择CONTA176，里面的管柱作为接触面，井壁作为目标面。

2.2 坐封过程压裂管柱有限元分析

2.2.1 定义坐封过程的约束和载荷

根据实际坐封施工情况，对管柱和井壁施加如下约束：由于管柱左端连接上部管柱，不考虑上部管柱变形，因此左端无轴向位移，压裂管柱左端全约束；右端施加x、z方向约束；因为不考虑井壁变形，因此井壁进行全约束。

在坐封过程中，由于压裂管柱内外存在22 MPa压差，而水平段液体压力为47.8 MPa，则在压裂管柱内外施加压力载荷分别为69.8和47.8 MPa；受坐封活塞效应的影响，需要在管柱右端施加轴向力120 kN。利用ACEL命令施加重力载荷。由于两封隔器之间管柱长度为80 m，通过摩阻效应理论计算，摩阻效应引起的轴向载荷相比内外压差和温度变化效应的轴向载荷较小，因此在仿真计算中不予考虑。

2.2.2 计算结果分析

水平段管柱竖直方向位移云图如图3所示。由图3可知，水平段压裂管柱在竖直方向上最大的位移为19.1 mm，与管柱外的环空间隙相等。在管柱两端被封隔器支承下，管柱受侧向力作用产生弯曲，与井壁产生接触，并且管柱中间有较长部分与井壁发生接触。从图3b可以看出，管柱中部截面上部的竖直位移比下部的竖直位移小，变形后的管柱截面半径增大，说明在内外压差作用下，管柱确实发生了鼓胀效应。

图3 竖直方向位移云图

压裂管柱整体应力分布云图如图4所示。由图4可知，水平段压裂管柱最大应力点在管柱右端，应力值为166.482 MPa，对比左端截面发现，应力值相同；因此，水平段压裂管柱最大应力分别在该段管柱两端，即和封隔器连接处。对于整体管柱，中部较长一段管柱的应力水平基本不变，而管柱两端应力较大，这是因为封隔器的支承约束导致局部刚度较大，在发生变形后，应力值也就较大。

图4 管柱整体应力分布云图

提取整段管柱中部单元，查看截面应力分布云图(见图5)可以发现，管柱外壁应力最小为121.635 MPa，管柱内壁应力最大为159.271 MPa。基于管柱强度校核计算方法，可求出管柱内壁应力理论值为156.34 MPa，外壁应力理论值为118.3 MPa，理论计算结果和有限元分析结果均相差≤5%。由现场试验提供的压裂管柱参数可知，压裂管柱的屈服强度为861.42 MPa，水平段管柱最大的应力值为166.482 MPa，远小于管柱的屈服强度。因此，有限元计算和理论计算的结果表明，该管柱组合的抗拉强度能够满足使用要求。

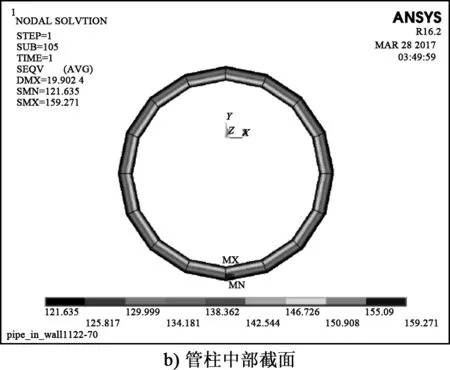
图5 管柱截面应力分布云图

3 弯曲段管柱有限元分析

3.1 弯曲段管柱有限元模型的建立

弯曲段起始点为水平井造斜点，垂深为3 319 m，弯曲段井眼曲率半径为271 m。弯曲段为套管封固段，套管段的摩擦因数为0.25，裸眼段的摩擦因数为0.3，套管外径为177.8 mm，壁厚为10.36 mm。压裂管柱外径为114.3 mm，壁厚为7.37 mm，钢级为P110，材料参数如下：弹性模量为2.06 GPa，泊松比为0.3，密度为7 800 kg/m3，屈服强度为757.54 MPa，抗拉强度为861.42 MPa。管柱设计安全系数为1.4。井口温度为20 ℃，井底温度为113.22 ℃。根据上述弯曲段井眼的数据，将弯曲段井眼轨迹简化为一段半径为271 m、圆心角为90°的圆弧，并根据管柱的几何形状对模型进行简化，建立的弯曲段压裂管柱模型如图6所示。

图6 弯曲段管柱模型

3.2 坐封过程压裂管柱有限元分析

3.2.1 约束和载荷

根据实际坐封施工情况，对管柱和井壁施加约束，由于管柱上端受直井段管柱轴向拉力作用，处于吊起状态，而管柱下端由于未完成坐封处于自由状态，因此管柱上端全约束，下端放开；不考虑井壁变形，因此井壁进行全约束。

在坐封过程中，由于A水平井井口施加了22 MPa压力，因此压裂管柱内外存在22 MPa压差，则在管柱内表面施加22 MPa压力。在坐封过程中，由于活塞效应会增加管柱轴向力变化，经过水平段管柱轴力传递，需要在弯曲段管柱下端施加120 kN的轴向载荷。利用ACEL命令施加重力载荷。根据该井实际温度变化梯度，在造斜点处设置105.61 ℃，水平点处设置113.22 ℃。

3.2.2 计算结果分析

在同样约束条件下，不施加内外压力，单独计算重力载荷作用下的管柱变形和轴向力，并与坐封条件下的结果进行对比，分析坐封过程内外压差对弯曲管柱的影响。重力作用下弯曲管柱竖直方向位移云图如图7所示。由图7可以发现，弯曲管柱竖直方向位移为64.503 mm，而该点的井斜角约为60°，管柱与井壁间的环空间隙为26.57 mm，那么未发生变形时，该点与井壁竖直方向上的距离为31 mm，因此，该点处的管柱与井壁发生了接触，并且由于上部管柱的伸长和下部管柱的压缩，使管柱竖直方向上的位移>31 mm。

图7 重力作用下弯曲管柱竖直方向位移云图

重力作用下弯曲管柱轴向力分布云图如图8所示。由图8可知，弯曲管柱上端，即造斜点处有最大轴向力51.31 kN，而管柱下端靠近水平段的部分管柱轴向力为压力。由水平井压裂管柱静态轴力计算式计算可得，弯曲段造斜点处确实存在最大轴向力，理论计算结果为50.67 kN。那么有限元计算结果和理论计算结果相差1.2%。

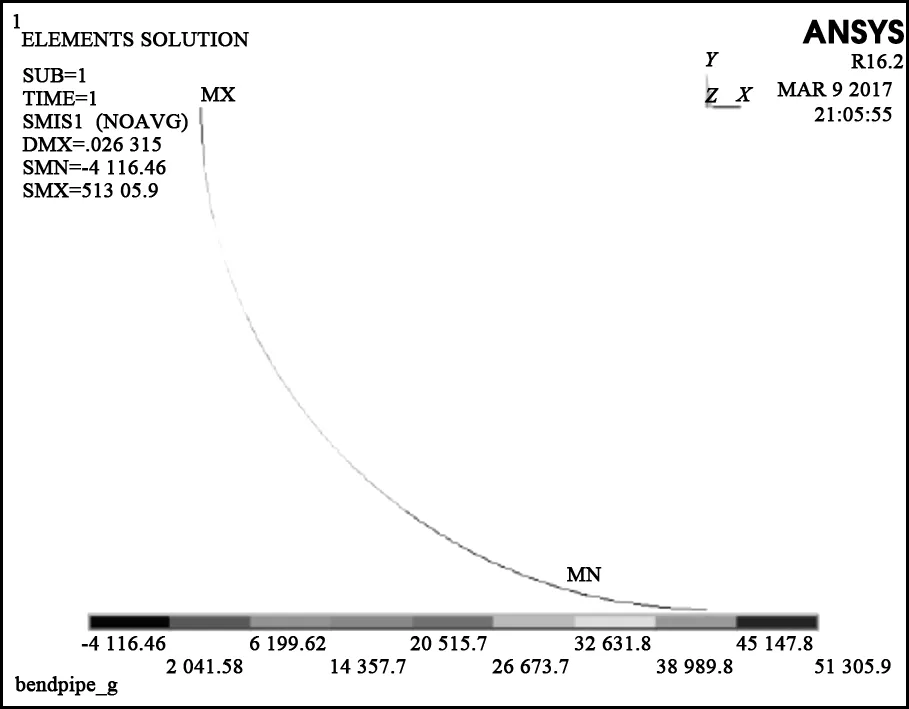
图8 重力作用下弯曲管柱轴向力分布云图

坐封过程的弯曲管柱轴向力分布云图如图9所示。对比重力作用下的结果可知，坐封过程存在的内外压差增大了弯曲管柱的轴向力，在上端有最大轴向力297.96 kN。对比重力作用下的最大轴向力可以看出，当管柱内压大于外压时，在压差的作用下管柱轴向力增大。通过理论计算得出，弯曲段管柱在坐封过程中的最大轴向力为274.3 kN，与有限元计算结果相差7.9%(<10%)。可见，由现场试验得到的压裂管柱参数可知，压裂管柱的抗拉强度为861.42 MPa，在弯曲段管柱最大轴向力处的轴向力为113.3 MPa，远小于管柱的抗拉强度，可见，该管柱组合的抗拉强度能够满足使用要求。

图9 坐封过程的弯曲管柱轴向力分布云图

3.3 压裂过程压裂管柱有限元分析

3.3.1 约束与载荷定义

根据实际压裂施工情况，对管柱和井壁施加约束：将坐封过程分析作为第1步，压裂过程分析作为第2步，在坐封过程计算完成后，对压裂管柱下端施加全约束；不考虑井壁变形，因此井壁进行全约束。

在压裂过程中，由于A水平井在压裂时井口施加了70 MPa压力，因此压裂管柱内外存在70 MPa压差，则在管柱内表面施加70 MPa的压力。重力载荷和温度载荷保持不变。而由于流体摩阻在管柱上引起的轴向载荷相比内外压差和温度载荷较小，因此在仿真计算中不予考虑。

3.3.2 计算结果分析

压裂过程的弯曲管柱轴向力分布云图如图10所示。由图10可知，轴向力最大点依然在造斜点处，最大值为412.349 kN。对比坐封过程的结果可以发现，内外压差越大，弯曲段管柱的轴向力增量就越大。由理论计算可得出，弯曲段管柱压裂过程中最大轴向力的理论值为445.1 kN，与有限元计算结果相差7.3%(<10%)。可见，该管柱组合的抗拉强度能够满足使用要求。

图10 压裂过程的弯曲管柱轴向力分布云图

[1] 窦益华，吕维平，张福祥，等. 支撑式跨隔测试管柱力学分析及其应用[J]. 石油钻采工艺，2007，29(4)：106-109.

[2] 毕博，朱卫新，白晶. 深井压裂井下管柱载荷与轴向变形研究[J]. 科学技术与工程，2010，10(10)：2284-2290.