深度神经网络代价函数选择与性能评测研究

赵 宏，郭万鹏

（1. 兰州理工大学计算机与通信学院，甘肃 兰州 730050；2. 兰州理工大学信息中心，甘肃 兰州 730050）

0 引言

人工神经网络ANN（Artificial Neural Networks）的研究是人工智能领域的一个重要分支，在对生物神经网络结构及其机制研究的基础上所构建的人工神经网络,使得机器能够直接从数据中提取特征和学习规律，从而使机器具有一定的智能。ANN的研究最早可以追溯到1957年Frank Rosenblatt提出的感知机模型，后来出现的反向传播 BP（Back Propagation）算法推动 ANN进入实用阶段[1]，但由于当时的ANN训练数据缺乏、训练方法及技巧不成熟、计算机运算能力不够强大等原因，使得这个时期的ANN结构较为简单，可等价为主要用来进行浅层学习的单隐层神经网络。2006年深度学习领域奠基人Hinton教授，根据人脑认知过程的分层特性，提出构建深度神经网络DNN（Deep Neural Networks），并取得成功[2]。

近年来，深度神经网络在图像识别、语音交互、自然语言处理等领域取得突破，进入实用阶段。与浅层神经网络相比，深度神经网络训练难度更大，其主要原因是梯度下降算法的残差值在网络中逐层传播时变得越来越小，出现梯度消失的问题，使得底层网络由于残差值过小而无法得到有效的训练。从模型训练经验可知，选择合适的代价函数并配合相应的激活函数能够明显改善梯度消失的问题，从而加快网络的训练速度。文献[3]对如何提高深度神经网络的学习速率做了大量的研究，并指出交叉熵代价函数能够避免深度神经网络学习速率缓慢的问题，但忽视了激活函数对代价函数性能的影响。文献[4]给出了一种改善深度神经网络训练效果的方法，指出改进激活函数能够提高深度神经网络的训练效果，但结果表明，仅对激活函数的改进，对于提高深度神经网络的学习速率效果并不明显。

利用概率论对模型训练中常用的二次代价函数和交叉熵函数进行理论推导，揭示两者在模型训练过程中对梯度下降算法参数的影响，研究代价函数与激活函数的组合效果，对模型训练过程中的经验进行理论解析并通过实验平台进行验证。

1 基本概念

1.1 独立同分布中心极限定理

定理1[5]设随机变量X1,X2,…,Xn相互独立，服从同一分布，且有 E (Xi) = μ , D (Xi) = σ2＞0,(i=1,2,…,n)，其中E(Xi)为随机变量 Xi的数学期望，D(Xi)为随机变量Xi的方差，则随机变量X1,X2,…,Xn之和Xi的标准化变量 Yn如式（1）所示。

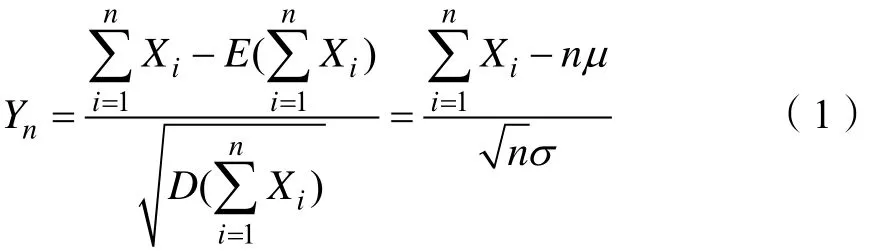
其中，对于任意的x，Yn的分布函数 Fn(x)满足式（2）。

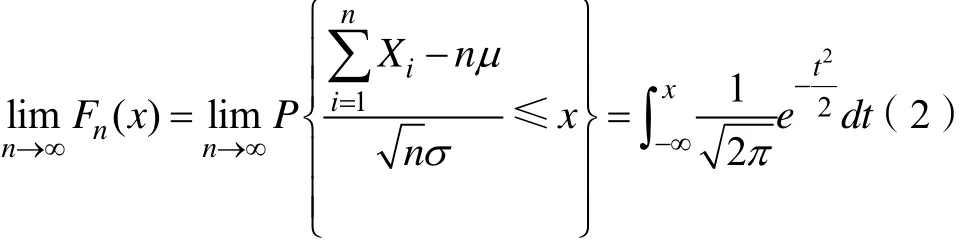
当n充分大时，若随机变量X1,X2,…,Xn服从独立同分布，期望为μ，方差为2σ ，则其和似地服从高斯分布N，如式（3）所示。

1.2 高斯分布

定义 1[6]如果随机变量x的概率密度函数如式（4）所示,则 x服从高斯分布 N ( μ,σ2)，记为x ～ N ( μ,σ2)，称x为高斯随机变量。其中，μ和σ为常数，且σ＞0。

1.3 似然函数

定义2[7]样本x1,…,xn的联合概率函数可看作θ的函数，用 L (θ; x1, x2,… ,xn)表示，称L(θ)为样本的似然函数，简记为L(θ)，如式（5）所示。

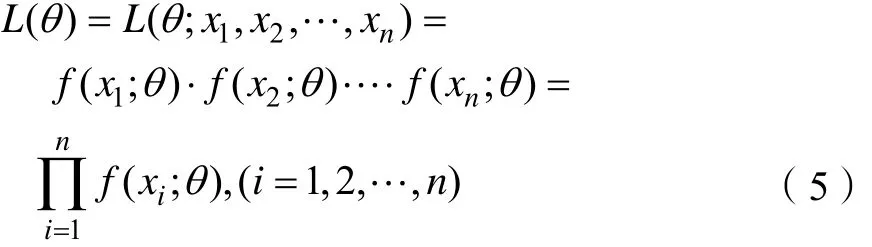
2 主要结论

2.1 二次代价函数

二次代价函数[8]的定义如式（6）所示。

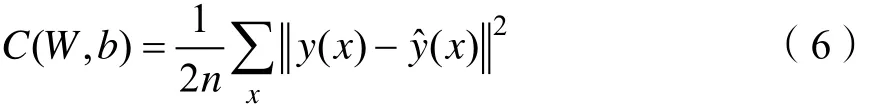
其中， (,)CWb表示神经网络的代价函数；n表示训练样本的大小；W和b分别表示由神经网络权重和偏置构成的矩阵。x表示由神经网络的输入构成的矩阵； ()yx表示由神经网络的预期输出构成的矩阵；ˆ()yx表示由神经网络的实际输出构成的矩阵。其中，ˆ()yx的表达式如式（7）所示。

其中，()δz表示激活函数。

由式（6）知，训练神经网络的最终目的是获得代价函数 (,)CWb最小时的权重和偏置，即神经网络的实际输出 ˆ()yx与预期输出 ()yx的误差最小时的权重和偏置。这是因为假设第i个神经元的实际输出为输入特征的线性函数与误差项之和，如式（9）所示。

其中，θ为给定的参数，ξ(i)为误差项，由定理1得由式（4）得高斯分布的概率密度函数如式（11）所示。

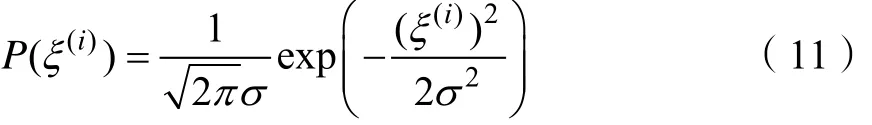
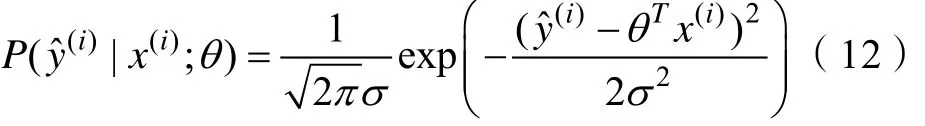
利用似然函数对参数θ进行估计。当θ为一定值时，以θ为参数的概率P取得最大值。由式（5）得

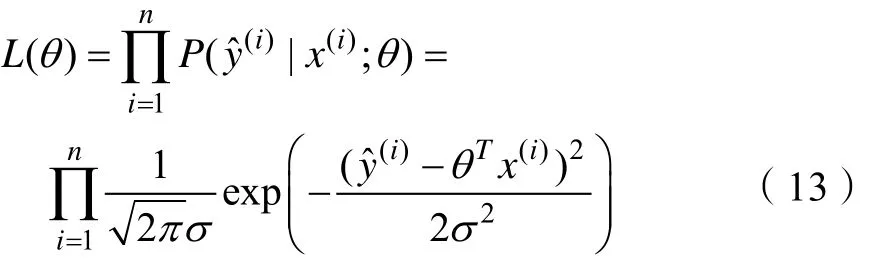
令 ℓ(θ) = log L (θ)，由式（13）得 ℓ(θ)

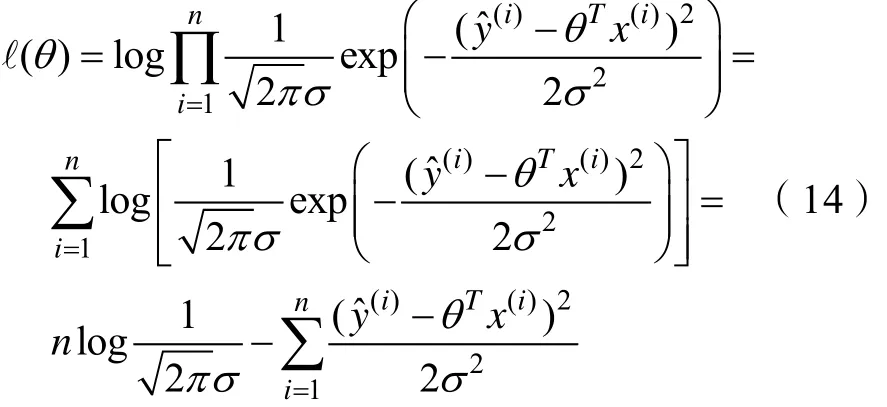
令

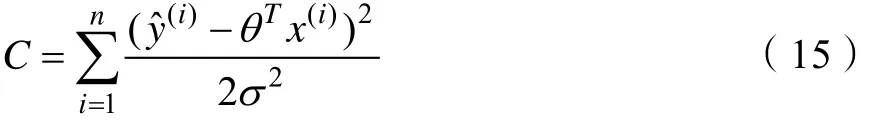
当函数()θℓ取得最大值时函数C取得最小值。对式（15）进行变换，令

则由式（15）、式（16）可得：

对式（6）进行链式求导得：

其中，假设神经网络的输入 x = 1，目标输出y(x) =0，则由式（17）、式（18）知，激活函数的导函数δ′(z)是影响权重和偏置学习速率的重要因素。

引入交叉熵代价函数能够消除δ′(z)对权重和偏置学习速率的影响。

2.2 交叉熵代价函数

假设 y = y1, y2,…yn是神经元上预期输出值，,, …是神经元上实际输出值，定义多元神经 元上交叉熵代价函数如式（19）所示。

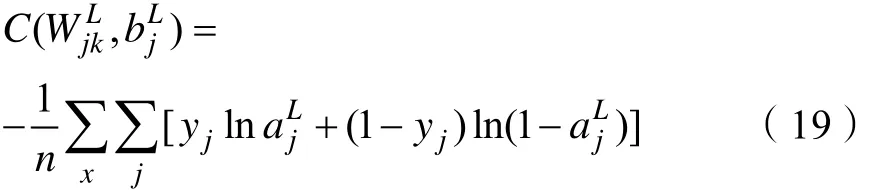
j的偏置；x表示神经元的输入。n表示训练样本的大小。引入交叉熵代价函数可以避免δ′(z)导致的神经网络学习速率缓慢的问题，这是因为在交叉熵代价函数中消除了参数δ′(z)的影响。由式（17）、式（18）得：

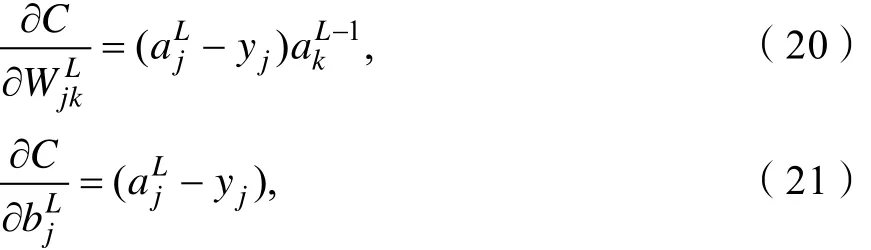
由式（7）得：

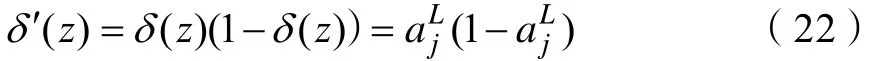
由式（6）得：

由式（21）、式（22）、式（23）得：

对式（24）求积分得：

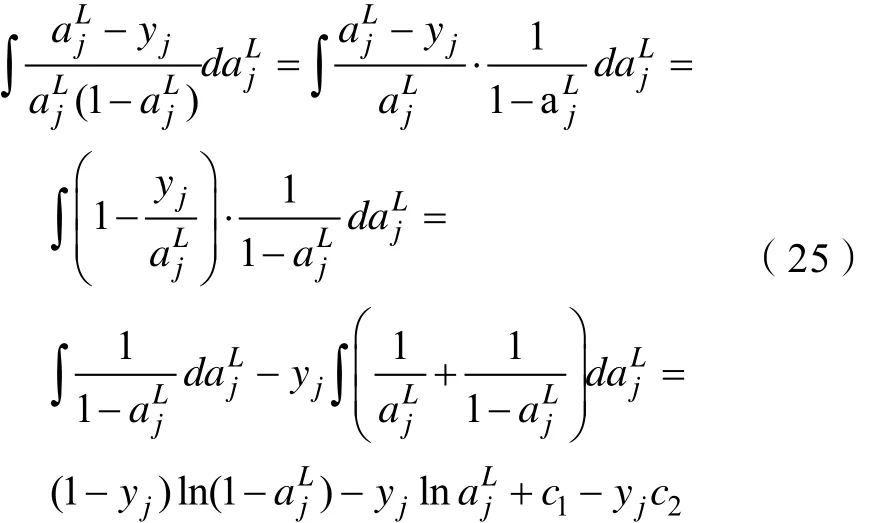
令 c = c1-yjc2，由式（25）化简得：

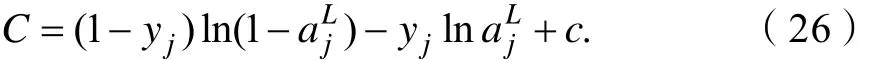
为了得到多元神经网络上整个交叉熵代价函数，对所有训练样本求平均，得式（19）。同时进一步证明了交叉熵能够解决多元神经元上δ′(z)导致学习速率缓慢的真正原因。式（19）中对参数进

行链式求导得：

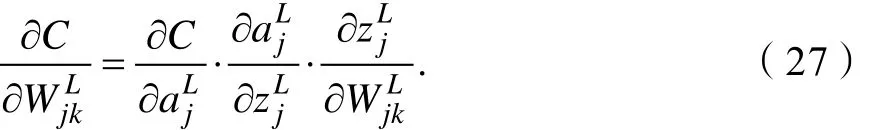
由式（19）得：

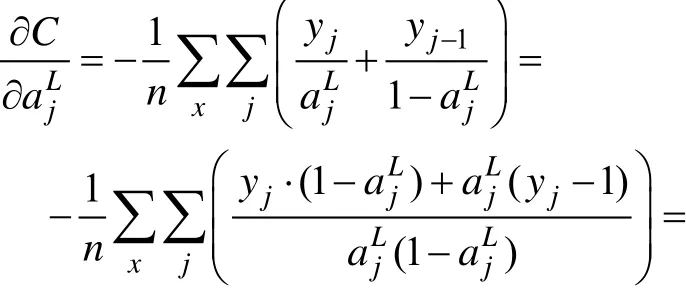
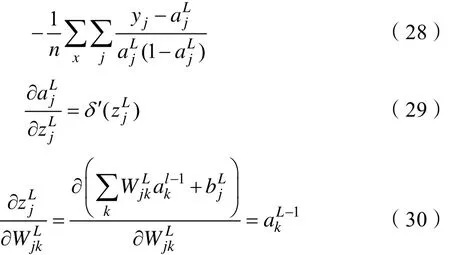
由式（28）、式（29）、式（30）得：

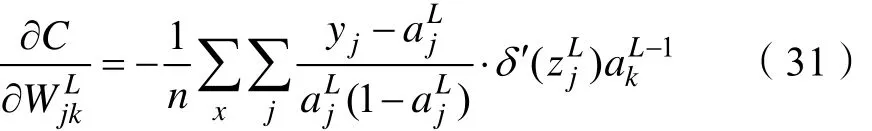
由式（22）、式（31）得：

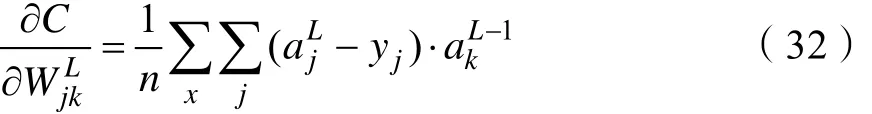
式（19）中对参数Ljb进行链式求导得

同理可得：

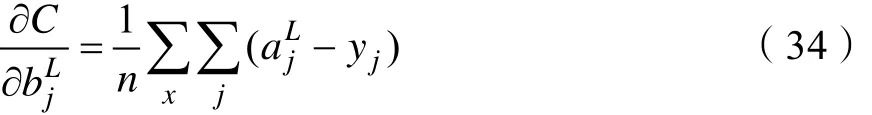
由式（32）、式（34）知，交叉熵代价函数消除了参数()δ′z，解决了多元神经元上()δ′z导致学习速率缓慢的问题。

通过对二次代价函数和交叉熵代价函数的推导可知，二次代价函数与非线性激活函数结合会导致权重和偏置的学习速率减慢，其真正原因是当()δ′z的值趋于0时，权重和偏置的学习速率受到抑制。引入交叉熵代价函数后，消除了()δ′z导致学习速率缓慢的问题，从而提高了权重和偏置的学习效率。另外，由式（20）、式（21）知，当神经网络的输入为一定值时，参数的学习速率会随输出误差的变化而变化，当输出误差较大时权重和偏置的学习速率也越快，这也是引入交叉熵代价函数后能够提高神经网络学习速率的重要原因。

由式（17）、式（18）知，不同激活函数导致代价函数学习速率的不同。因此，需要进一步分析代价函数和激活函数组合后的神经网络性能。

2.3 激活函数

神经网络中常用的激活函数分别为 Sigmoid、Tanh、ReLu和 PReLu。

2.3.1 Sigmoid 激活函数

Sigmoid函数表达式如式（35）所示，函数值在0到1之间，如图1所示。Sigmoid激活函数具有双向饱和的特性，当x→∞时，σ′(x) =0，具有这种性质的激活函数称为软饱和激活函数[9]，Sigmoid激活函数的软饱和性是导致神经网络学习速率缓慢的重要原因。

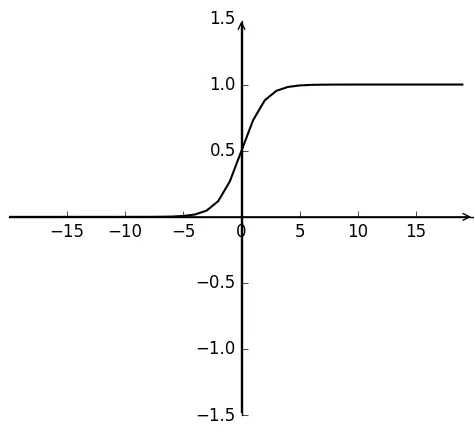
图1 Sigmoid函数Fig.1 Sigmoid function

2.3.2 Tanh激活函数

Tanh函数与Sigmoid函数具有相似的性质，是典型的S型函数，表达式如式（36）所示，函数值在-1到1之间，如图2所示。相比Sigmoid函数，Tanh函数延迟了饱和期。对比图1和如图2可知，Tanh函数与Sigmoid函数一样具有软饱和的特性，同样会陷入局部最优解，使神经网络训练难度加大，但Tanh函数性能优于Sigmoid函数。

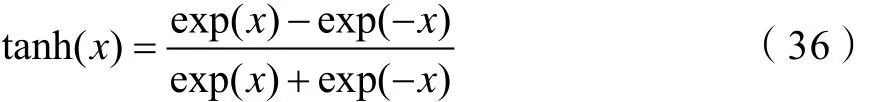
图2 Tanh函数Fig.2 Tanh function

2.3.3 ReLu激活函数

Relu函数表达式如式（37）所示，函数值为 0或x，如图3所示。Relu激活函数避免了S型激活函数饱和区对神经网络收敛速度的限制[10]，但是Relu激活函数在训练时非常脆弱，流经ReLu神经元的一个大梯度导致权重更新后该神经元接收到的任何数据点都不会再被激活。

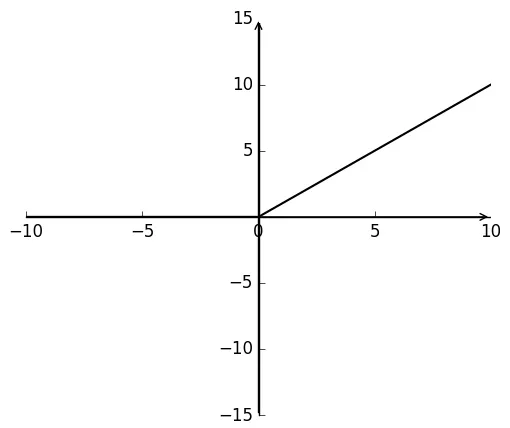
图3 ReLu函数Fig.3 ReLu function

2.3.4 PReLu激活函数

PReLu（Parametric ReLu）函数表达式如式（38）所示，函数值根据x的不同为斜率不同的直线，如图4所示。PReLu激活函数在ReLu激活函数的基础上作了进一步改进，当x为负值时其导数不再为0。

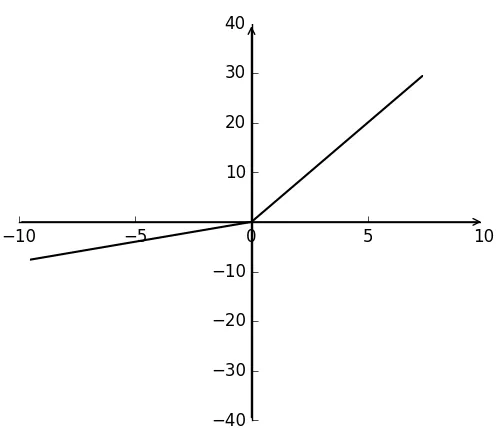
图4 PReLu函数Fig.4 PReLu function

3 实验分析

3.1 CNN模型原理

卷积神经网络 CNN（Convolutional Neural Network）作为神经网络最常见的形式，使用代价函数和激活函数的组合来提高网络的训练效率和精度。CNN通过激活函数映射网络的输出，利用代价函数对网络的输出误差进行评价，进而使用反向传播算法和随机梯度下降算法不断提高网络的精度。同时CNN的局部感知域、权值共享和池化层等三个主要特征[11]对大型图像的处理具有出色的表现。基于Hubel和Wiesel早期对猫初级视觉皮层（V1）的研究，CNN基本结构[12]如图5所示，由输入层、卷积层、池化层、全连接层和输出层组成。其中，卷积层和池化层是卷积神经网络特有的属性。卷积层通过卷积操作提取输入的不同特征，池化层对卷积层提取的特征进行池化处理，保留最有用特征，减少神经元数量，避免网络发生过拟合，最后利用softmax分类器进行分类，并通过全连接层输出结果。

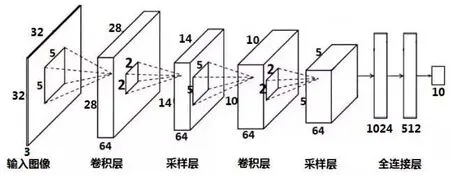
图5 卷积神经网络的模型图[13]Fig.5 The model of convolution neural network

3.2 多通道卷积操作

卷积层是CNN核心网络层，卷积层基于图像空间的局部相关性，利用卷积提取图像的局部特征，如图6所示。

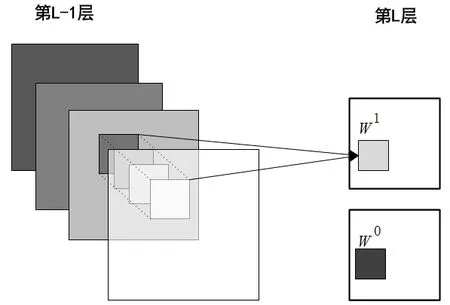
图6 多通道卷积网络结构[14]Fig.6 The network structure of multi-channel convolutional

第L层特征的计算公式如式（39）所示。

其中，z表示第L层特征的输入；WjLk-1表示第L- 1层的第j个神经元与第k个神经元之间的权重；bLj-1表示第L- 1层上第j个神经元的偏置；x表示第L- 1层的输入。

输出图像特征的计算如式（40）所示[14]。

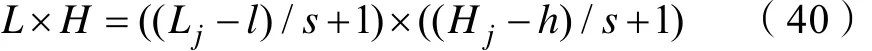
其中，L×H表示输出图像尺寸；Lj×Hj表示第j个神经元上输入图像尺寸；l×h表示滤波器尺寸；s表示滑动步长。

3.3 池化操作

池化操作是对卷积层提取的特征进行处理，其目的是降低卷积层输出的特征向量，避免网络发生过拟合，同时改善网络训练效果。理论上，可以用所有提取到的特征去训练分类器，但这样做面临计算量的挑战。例如，对于一个96×96像素的图像，假设已经学习得到了400个定义在8×8输入上的特征，每一个特征和图像卷积都会得到(96 - 8 + 1 )×(96 - 8+ 1 ) = 7 921维的卷积特征，由于有400个特征，所以每个样例都会得到7921×400=3168400维的卷积特征向量，训练这样一个超过3000000特征输入的分类器容易出现过拟合。根据图像的“静态性”属性，池化操作对卷积层进行如图7所示的处理，可以有效防止特征过多造成过拟合的问题，其池化的主要策略有mean-pooling、max-pooling、stochasticpooling等。

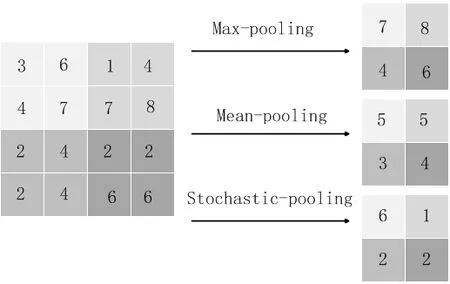
图7 池化过程Fig.7 Pooling process

3.4 模型构建

通过对CNN模型原理的分析，利用Google深度学习平台TensorFlow构建了以CNN模型为基础的深度神经网络，其中，网络的构建采用了代价函数和激活函数不同组合的方式，并利用 notMNIST数据作为实验数据集。notMNIST数据集是一组按字符分类的图像文件夹，有A、B、C、D、E、F、G、H、I、J共10个文件夹，其可视化后的效果如图8、图9所示，其中，训练数据集中含有部分非字符的噪声图像，如图9所示。

3.5 实验结果

表1、表2、表3、表4分别为 Sigmoid、Tanh、Relu和PReLu为激活函数时与二次代价函数和交叉熵代价函数的组合效果，表5为实验中采用的超参数值。

图8 notMNIST测试数据集Fig.8 Test dataset of notMNIST

图9 notMNIST训练数据集Fig.9 Training dataset of notMNIST

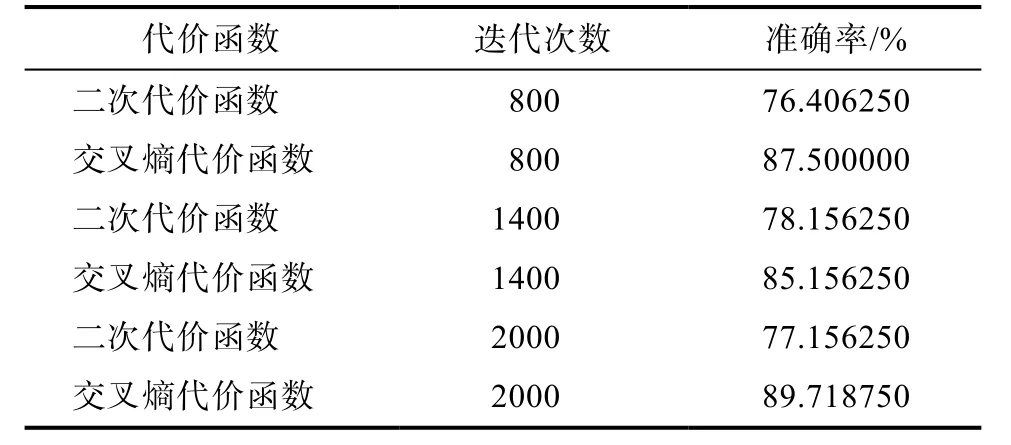
表1 Sigmoid作为激活函数时性能对比Tab.1 Performance comparison while Sigmoid as the activation function

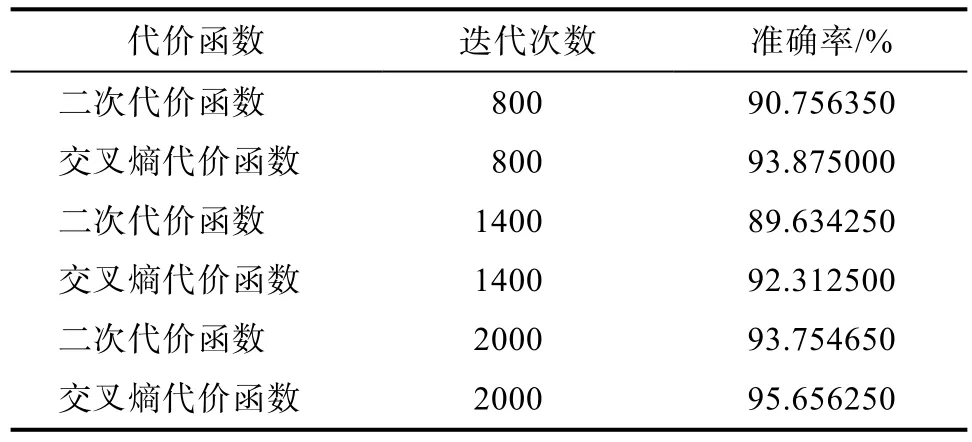
表2 Tanh作为激活函数时性能对比Tab.2 Performance comparison while Tanh as the activation function

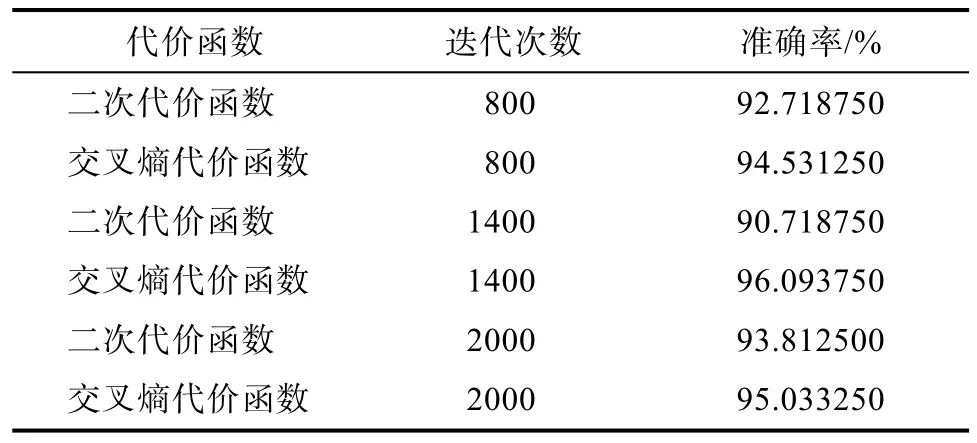
表3 ReLu作为激活函数时性能对比Tab.3 Performance comparison while ReLu as the activation function

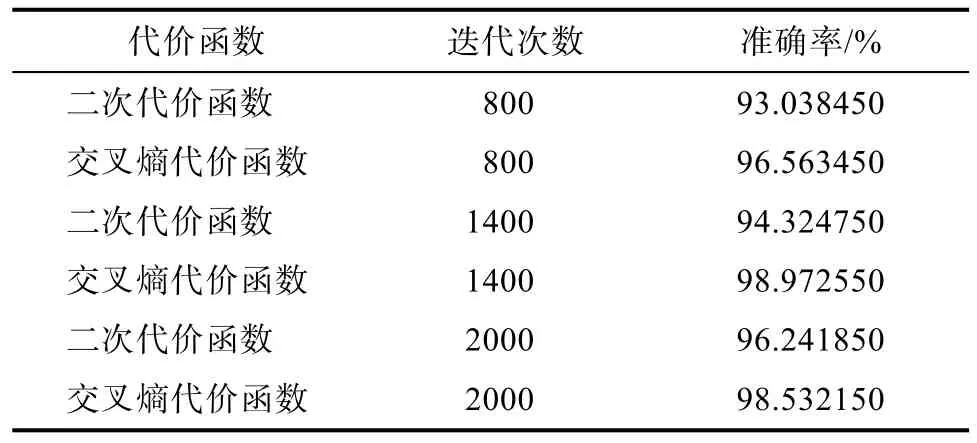
表4 PReLu ReLu作为激活函数时性能对比Tab.4 Performance comparison while PReLu as the activation function

表5 实验中超参数的具体值Tab.5 The specific value of the over-parameter in the experiment

3.6 实验结果分析

实验探索了不同代价函数和激活函数组合下模型训练的性能，发现代价函数和激活函数的优选会影响模型的训练效率。通过实验结果的对比发现，线性激活函和非线性激活函数对二次代价函数的性能有不同的效果，究其原因，线性激活函数的导函数是一个常数，对二次代价函数的性能并不产生影响，而Sigmoid和Tanh等非线性函数容易达到饱和导致梯度消失，所以导致学习速率缓慢。实验也表明系统采用 ReLu函数以及 ReLu函数的变体函数PReLu与代价函数结合使用，会明显改善训练的效果，这是因为Relu函数可以通过简单的零阈值矩阵进行激活，并且不受饱和的影响，但是，Relu函数在训练时非常脆弱，流经 ReLu神经元的一个大梯度导致权重更新后该神经元接收到的任何数据点都不会再激活。为了解决这个问题，研究者们发现了ReLu函数的一些变体函数，如PReLu，与交叉熵代价函数结合具有良好的训练效果。最后，实验对超参数的设置也进行了探究，并给出了针对该实验具有良好效果的超参数值。

4 结语

本文利用概率论对模型训练中常用的二次代价函数和交叉熵代价函数进行推导，揭示了两者在模型训练过程中对参数寻优的影响，并给出了它们与不同激活函数组合的效果。实验表明，代价函数与激活函数的优选能够减少训练的迭代次数，从而提高深度神经网络训练的效率。并且发现交叉熵代价函数与PReLU激活函数结合具有优秀的效果。

[1] 庞荣. 深度神经网络算法研究及应用[D]. 西南交通大学,2016.

[2] Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786):504-507.

[3] Michael A. Nielsen. Neural Networks and Deep Learning[M].Determination Press, 2015.

[4] 叶小舟, 陶飞飞, 戚荣志, 等. 循环神经网络结构中激活函数的改进[J]. 计算机与现代化, 2016(12): 29-33.

[5] 邹广玉. 混合随机变量序列的几乎处处中心极限定理[D].吉林大学, 2013.

[6] Zhao L, Mi D, Sun Y. A novel multitarget model of radiationinduced cell killing based on the Gaussian distribution[J].Journal of Theoretical Biology, 2017, 420: 135-143.

[7] 王晓红, 李宇翔, 余闯等. 基于β似然函数的参数估计方法[J]. 北京航空航天大学学报, 2016, 42(1): 41-46.

[8] 徐先峰, 冯大政. 一种充分利用变量结构的解卷积混合盲源分离新方法[J]. 电子学报, 2009, 37(1): 112-117.

[9] Bao G, Zeng Z. Analysis and design of associative memories based on recurrent neural network with discontinuous activation functions. Neurocomputing[J]. Neurocomputing, 2012,77(1): 101-107.

[10] 张尧. 激活函数导向的RNN算法优化[D]. 浙江大学, 2017.

[11] 卷积神经网络在图像分类中的应用研究[D]. 电子科技大学, 2015.

[12] 何鹏程. 改进的卷积神经网络模型及其应用研究[D]. 大连理工大学, 2015吴正文.

[13] 李彦冬, 郝宗波, 雷航. 卷积神经网络研究综述[J]. 计算机应用, 2016, 36(9): 2508-2515.

[14] 张重生 深度学习: 原理与应用实践[M]. 电子工业出版社,2016.