基于耦合忆容模拟器的双非门振荡电路

周 知，朱 旺，朱 虹，于东升

（中国矿业大学电气与动力工程学院，徐州 221116）

2008年惠普实验室成功研制出基于二氧化钛薄膜的纳米级忆阻器件[1]，2009年蔡少棠等又在忆阻器的基础上推测出忆容器和忆感器的存在[2]。忆容器是一种具有记忆特性的容性电子元件，其表征的是电荷积分和磁通的关系[3]。因尚无商用的忆容器件，目前对忆容器的研究多采用仿真或等效电路模型[4，5]，但多存在一端必须接地的限制[6，7]。 已有文献介绍了关于忆容器的并联、串联[8]以及基于忆容器非线性电路的混沌行为[3，9～11]，但对双忆容器的耦合行为的研究较少。耦合是大规模纳米级忆容器集成电路中不可忽视的一种物理现象[12]，研究耦合型忆容器的动态和稳态特征对优化和推广忆容器及其应用电路具有重要意义。为了便于研究耦合型忆容模拟器的特性，设计简单、实用的耦合型忆容器模拟电路是十分必要的。

磁通控制型忆容器的电荷-电压关系[13]可以表示为，其中，Cm为忆容器忆容值，vc（t）为端电压，qc（t）为忆容器两端的电荷。传统的双非门多谐振荡电路利用一个交叉耦合反馈网络、一个没有外部触发信号的延时电容和具有阈值开关特性的非门即可稳定输出连续的方波信号[14]。 不像单稳态振荡器[15]或双稳态振荡器[16]需要一个外部的触发脉冲，自激多谐振荡器不需要外部的触发脉冲，可以产生稳定的自激振荡[17]。目前鲜有关于耦合忆容器的多谐振荡电路的研究，本文研究了由1对耦合忆容模拟器、4个非门和4个电阻组成的基于耦合忆容模拟器的多谐振荡电路，每个忆容模拟器由6个有源芯片构成[18]，并经由加法电路形成等效耦合关系。本文基于文献[13]设计了一种无接地限制的忆容模拟器，进一步设计了磁通耦合双忆容器模拟电路，并基于此耦合忆容器，研究了基于耦合忆容模拟器的双非门多谐振荡电路的动态特性，且其输出特性可用于电力电子变换器的驱动和信号测试。

1 磁通控制型耦合忆容模拟器

本文设计的独立忆容模拟电路包含6个有源器件：4个跨导运算放大器（AD844）、1个模拟乘法器（AD633）和1个运算放大器（TL084）。忆容模拟电路同时由7个电阻和2个电容元件及辅助有源器件完成运算工作。将2个忆容模拟器电路中的耦合接口通过一定的方式连接，即可形成磁通控制型耦合忆容模拟器，如图1所示。

2个忆容模拟器MC1和MC2的端口均为悬浮端口，MC1的耦合接口连接至MC2电路中U32的输出端，MC2的耦合接口连接至MC1电路中U31的输出端。因U31和U32的输出端电压分别与忆容器端电压vA1B1和vA2B2成线性比例关系，2个忆容模拟器之间形成了磁链耦合关系，工作状态通过磁链相互影响。2个忆容器耦合关系的建立，是通过电位器将一个忆容模拟器中的磁链信号传送到另一个忆容模拟器内部加法器的反相输入端，共同参与忆容值的控制运算。

耦合忆容器电路中忆容器的忆容值分别为

图1 磁通控制型耦合忆容模拟器原理Fig.1 Schematic of flux-controlled coupling memcapacitor simulator

式中：α1、α2为忆容值的变化率，F/Wb，β1、β2为忆容值的初始值，F；k1和k2为耦合系数，F/Wb。可分别表示为

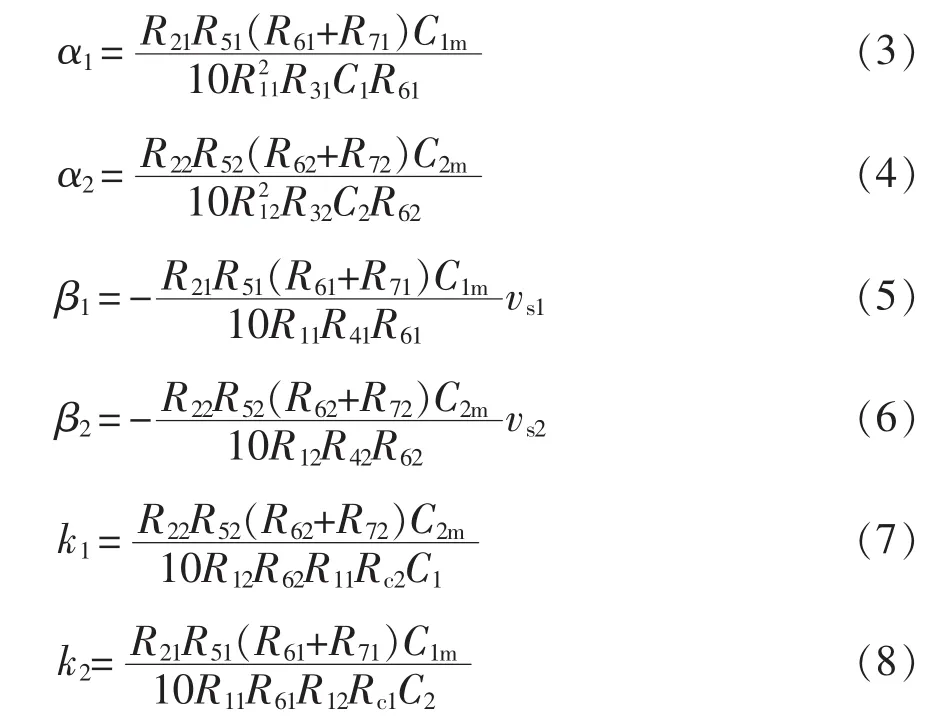
式（7）和式（8）表明，通过改变忆容模拟器中耦合电阻Rc1和Rc2即可方便地调节耦合忆容模拟器电路的耦合强度，以便于研究不同耦合系数对耦合忆容器电路动态特性的影响。

在耦合忆容模拟器的输入端分别外加正弦激励，取 vA1B1=2sin（40πt）V，vA2B2=2sin（60πt）V，观察忆容模拟器的忆容特性。对忆容器MC1，电容C1m两端的电压和流过忆容模拟器的电荷成正比，又由AD844的工作特性：x脚电压跟随y脚电压，因此可以通过测量U41-AD844的y脚电压vw1来代替忆容模拟器的电荷qMC1，所以可以用vw1～vA1B1的函数关系表示磁通控制型忆容模拟器的忆容特性qMC1-vA1B1。同理，对忆容器MC2，可以用vw2-vA2B2的函数关系来表示磁通控制型忆容模拟器的忆容特性qMC2-vA2B2。Pspice仿真得到耦合忆容模拟器耦合忆容特性如图2所示。时域曲线如图2（a）所示。在时域0.20～0.25 s范围内，vw1与vA1B1在t=0.225 s处相交；vw2与 vA2B2分别在 t=0.216 7、0.233 3、0.25 s处相交。

为进一步观察耦合忆容模拟器的耦合忆容特性，使用图 2（a）中的数据，以 vA1B1和 vA2B2为 x轴，以vw1和vw2为y轴，得到其耦合忆容特性曲线如图2（b）所示。图2（b）所示为耦合后的2个忆容模拟器的耦合忆容特性曲线，它们均具有忆容特性，其电荷-电压的波形均为过原点（0，0）的‘8’字形Lissajous曲线，且Lissajous曲线在第1象限的封闭面积等于在第3象限的封闭面积。由于vA2B2的频率为30 Hz，大于vA1B1的频率20 Hz，所以vw2-vA2B2的Lissajous曲线与x轴夹角小，且紧滞环更加扁。

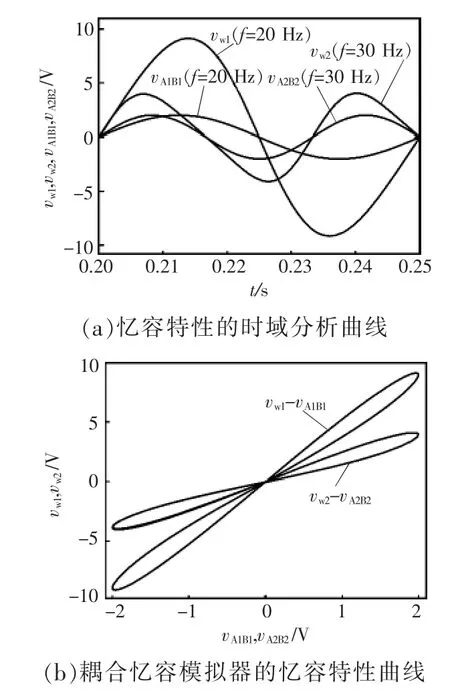
图2 仿真结果Fig.2 Simulation results

2 耦合忆容模拟器的双非门振荡电路

传统的双非门振荡电路原理如图3所示，其电路由2个非门（CD4096）、1个反馈系统和1个输出端组成。双非门振荡电路中高阻值电阻R1的作用是保护非门的输入端，限制流入非门的电流。

根据传统双非门振荡电路的充电放电过程，为了进一步分析其输出电压的振荡行为，用Pspice对传统双非门振荡电路进行仿真，得出传统双非门振荡电路的时域输出特性vo/vc/vf曲线如图4所示。

非门的输出电压vo为-VCC或VCC（±VCC为非门CD4069的供电电压），根据电容C的充电或者放电状况，电路有2种工作状态，存在VHth和VLth2个门槛电压，使非门在高低电平之间跳动。充电时，电压vf和忆容器电压vc相等，vf从-10-VLth上升到 VLth，输出电压vo维持在低电压，直到vf到达VLth，在vf= VLth时，输出电压 vo从低电平跳到高电平，电路进入放电状态；放电时，vf从10-VHth减小到VHth，输出电压vo保持在高电平，直到vf达到VHth，当vf=VHth，电路重新回到充电状态，输出电压vo从高电平回到低电平。因此，电路周期和频率可表示为

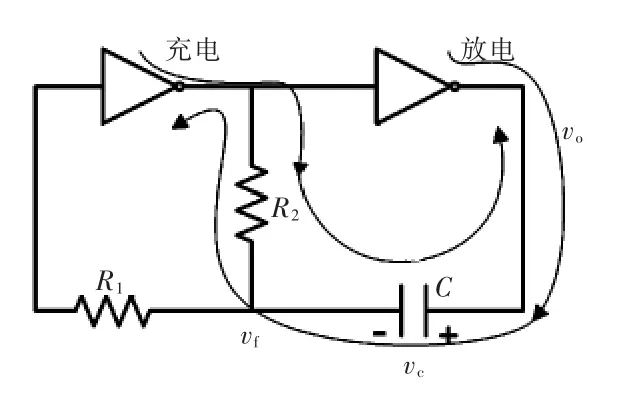
图3 传统双非门振荡电路原理Fig.3 Schematic of a traditional two-astableoscillator circuit

图4 传统双非门振荡电路的输出特性曲线Fig.4 Output characteristic curves of a traditional twoastable-oscillator circuit

基于耦合忆容模拟器的双非门振荡电路由4个非门、4个普通电阻和1对耦合忆容模拟器组成，其电路原理如图5所示，即在耦合忆容模拟器的双非门振荡电路中，用耦合忆容模拟器代替2个双非门振荡电路中的2个普通电容，其中耦合忆容模拟器是由2个忆容模拟器经耦合电位器耦合而成，然后在耦合忆容模拟器的2个忆容模拟器的两端分别接一个双非门振荡电路。

图5 基于耦合忆容模拟器的双非门振荡电路原理Fig.5 Schematic of the two-astable-oscillator circuit based on coupling memcapacitors simulator

双非门振荡电路中无论是否含有忆容模拟器，其输出电压的频率公式中常系数是不变的。因此，耦合忆容模拟器的2个弛张振荡电路的输出电压频率分别为

取Rs1=500 kΩ、Rs2=80 kΩ时，用Pspice仿真得到双非门振荡电路的输出特性 vo1/vo2/vf1/vf2/vCM1/ vCM2，曲线如图6所示。图中,vCM1=vf1-vo1，vCM2=vf2-vo2。以CM1侧双非门振荡电路为例，充电时，电压vf1和忆容器电压vCM1相等，vf1从-10-VLth上升到VLth，输出电压vo1维持在低电压直到vf1到达VLth，在vf1= VLth时，输出电压vo1从低电平跳到高电平，电路进入放电状态；放电时，vf1从10-VHth减小到VHth，输出电压vo1保持在高电平直到vf1达到VHth，当vf1=VHth，电路重新回到充电状态，输出电压vo1从高电平回到低电平。CM2侧双非门振荡电路的充放电状态与CM1侧双非门振荡电路一致。

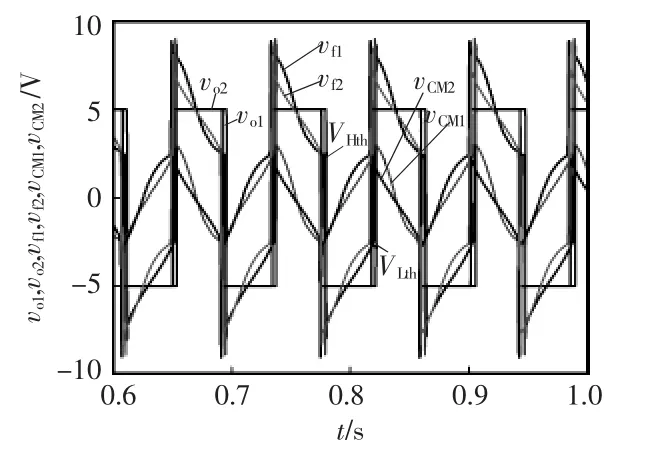
图6 双非门振荡电路的输出特性仿真曲线Fig.6 Simulation of outputs characteristics from a two-astable-oscillator circuit

为了观察2个双非门振荡电路中的耦合忆容模拟器的忆容特性，对忆容特性进行时域分析，如图7所示。以图1中忆容器MC1为例，流过忆容模拟器 MC1的电荷可表示为：qCM1=C1mvc1m=C1mvw1，因此，为测量方便，可以通过测量电压vw1来代替MC1的电荷qCM1。同理，可以通过测量vw2来代替MC2的电荷qCM2。取耦合电位器的电阻值为Rc1=500 kΩ，Rc2=450 kΩ，测量耦合忆容模拟器的忆容特性的时域曲线如图7（a）所示。

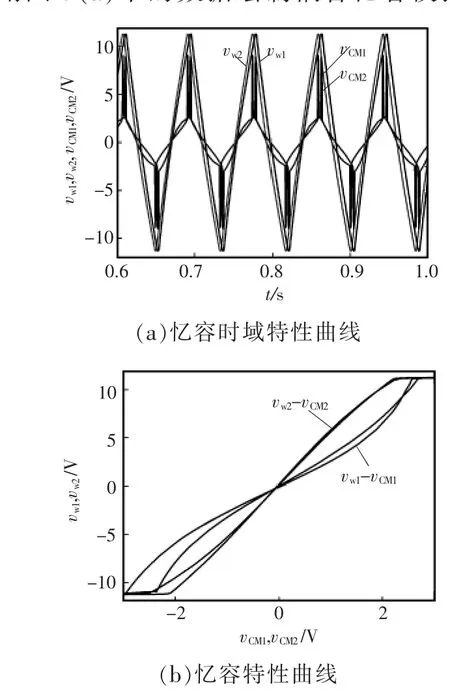
图7 双非门振荡电路中耦合忆容模拟器仿真结果Fig.7 Simulation results of two coupling memcapacitance simulator in two-astable-oscillator

用图7（a）中的数据绘制耦合忆容模拟器的忆容特性曲线，x轴分别为vCM1和vCM2，对应y轴分别为vw1和vw2。得到双非门振荡电路中的耦合忆容模拟器的忆容模拟特性曲线vw1-vCM1（vw2-vCM2）如图7（b）所示。在耦合忆容模拟器的双非门振荡电路中的忆容模拟器仍然具有忆容特性，忆容模拟器的电荷-电压仍然呈现‘8’的形状且过原点（0，0）。vw1-vCM1在第一象限低于vw2-vCM2，这和图7（a）中y轴正半轴，CM2侧的双非门振荡电路的输出特性曲线vw2超前CM1侧的双非门振荡电路的输出特性曲线vw1相符。vw1-vCM1在第三象限高于vw2-vCM2，这和图7（a）中y轴负半轴CM2侧的双非门振荡电路的输出特性曲线vw2超前CM1侧的双非门振荡电路的输出特性曲线vw1相符，且vw2-vCM2下降得更快。

3 实验验证

为了证实其理论分析和仿真结果的正确性，对基于耦合忆容模拟器的双非门振荡电路的硬件电路进行实验，实验数据由TDS2024C示波器采样，用OriginPro 8绘制实验波形曲线。

3.1 耦合忆容器的双非门振荡电路的设计

由图1可以看出，单个忆容模拟器由4个跨导运算放大器 （AD844）、1个模拟乘法器（AD633）、1个运算放大器（TL084）和若干电容电阻组成。图1上面虚线封闭的框图内是一个独立的忆容模拟器（用MC1表示）。同样地，下面虚线封闭的框图内也是一个独立的忆容模拟器（用MC2表示）。每个忆容模拟器的忆容值，可以通过调节耦合电位器阻值RC1、RC2改变（由式（1）、式（2）、式（7）、式（8）可知）。由图5可以看出，耦合忆容模拟器的双非门振荡电路由1对耦合忆容模拟器、4个非门（CD4069UB E）、4个电阻组成。基于耦合忆容模拟器的双非门振荡电路是用耦合忆容模拟器取代2个多谐振荡电路中的2个普通电容，其中耦合忆容模拟器是由2个忆容模拟器通过耦合电位器并联耦合得到的，且2个忆容模拟器是通过相同的极性并联的。

以MC1侧为例，电荷q-电压v可以用AD633-U61的输出电压vw1和忆容模拟器两端的电压vCM1表示，由AD844的特性，即在实验中通过测量电容Cm1两端的电压vc1m和双非门振荡器电路中CD4069的2号脚vf1减去vo1可得vCM1。同理，也可以测得MC2侧的忆容关系曲线。

3.2 实验分析

实验分析主要包括两个部分，一是对耦合忆容模拟器的耦合忆容特性进行实验验证，二是对基于耦合忆容模拟器的双非门振荡电路的输出特性进行实验验证。

耦合忆容模拟器的实验参数如表1所示。Rc1和Rc2选用最大阻值为1 MΩ的电位器，用来平滑地调节耦合忆容模拟器的耦合系数。

表1 耦合忆容模拟器的实验参数Tab.1 Experimental parameters of coupling memcapacitors simulator

基于表1数据，由式（3）、式（4）可以得出忆容变化率为α1=α2=1.316 9×10-6F/Wb，由式（5）、式（6）忆容初始值为β1=β2=9.409 6×10-8F。当取电位器阻值 Rc1=500 kΩ、Rc2=450 kΩ 时，k1=9.231 4×10-7F/ Wb，k2=1.025 7×10-7F/Wb，当MC1侧的激励电压为正弦电压vA1B1=2 sin（40πt）V、MC2侧的激励电压为正弦电压vA2B2=2 sin（60πt）V时，耦合忆容模拟器的实验结果如图8所示。将耦合忆容模拟器MC1侧和MC2侧的忆容特性实验数据分开测量，再用OriginPro 8绘制耦合忆容模拟器的忆容特性曲线。对比发现，图8和图2几乎一致，由此可以验证理论分析和仿真结果的正确性。曲线vw1-vA1B1与曲线vw2-vA2B2的夹角比仿真图中的夹角小，主要是为了使耦合特性更加明显，耦合电位器Rc1和Rc2与仿真时取值不同。此外，硬件电路中元器件的数值由于制作工艺也有一定的误差，并且电路的连接线存在阻值，也会对实验结果造成一定的干扰。

图8 耦合忆容模拟器的忆容特性曲线实验结果Fig.8 Memcapacitance characteristic curves of experimental results coupling memcapacitors simulator

耦合忆容模拟器的双非门振荡器电路的实验参数如下，Rp1=500 kΩ，Rp2=80 kΩ，Rs1=500 kΩ，Rs2= 80 kΩ，非门选择型号为CD4069UBE的14引脚芯片。观察双非门振荡电路的输出vo1/vo2/vf1/vf2的电压变化情况和此时耦合忆容模拟器的忆容特性vCM1/vCM2/vw1/vw2时域分析曲线。双非门振荡电路的输出情况分析图9（a）所示，耦合忆容模拟器的忆容特性时域分析曲线如图9（b）所示。

图9（a）为双非门振荡电路的输出曲线，和图7（b）相比，图9（a）中CM1侧双非门振荡电路的输出和CM2侧双非门振荡电路的输出的相位差更小一些，这是因为实验过程中为了使耦合特性更加明显，耦合电位器Rc1、Rc2和仿真时取值不同。此外，图9（a）中2个双非门振荡电路的输出电压 vo1/vo2在0和5 V之间跳动，这是因为实验过程中非门芯片的供电电压为5 V和0 V。由于vCM=vf-vo，为了观察更加清晰，所以未测量vCM1和vCM2的曲线。

双非门振荡电路中耦合忆容模拟器的忆容曲线时域分析实验结果如图9（b）所示，和图7（a）基本保持一致。和图7（a）相比，因为实验中选用的非门芯片精度更高，vCM1/vCM2最大值和最小值处的尖峰长度明显减小，且vw1/vw2的曲线在峰值处也更加圆滑。此外，由于在硬件实验中元器件的参数由于制作工艺等原因和仿真数据有一定的差距，电路中导线的焊接工艺的缺陷也会对实验结果造成一定的误差等，均导致图9（b）和图7（a）未能完全吻合。由于上述原因对实验结果的影响较小，因此误差基本可以忽略不计。

图9 双非门振荡电路实验结果Fig.9 Experimental results of the two-astable-oscillator

4 结语

本文设计了耦合忆容模拟器和基于耦合忆容模拟器的双非门振荡电路，并分析了其工作原理。利用Pspice对耦合忆容模拟器和基于耦合忆容模拟器的双非门振荡电路进行仿真，并搭建了硬件电路进行实验验证。实验结果与仿真结果吻合，证实了基于耦合忆容模拟器的双非门振荡电路的可行性，同时也表明，忆容模拟器既可用于浮动耦合并联连接，也可用于双非门振荡电路中的接地连接。基于耦合忆容模拟器的双非门振荡电路可提供更为多样化的方波信号，可用于电力电子变换器的驱动和信号测试。本文的研究结果对今后开发忆容模拟器并应用于各种电力电子电路具有参考价值。

[1]Strukov D B,Snider G S,Stewart D R,et al.The missing memristor found[J].Nature,2008,453（7191）：80-83.

[2]Ventra M D,Pershin Y V,Chua L O.Circuit elements with memory：memristors,memcapacitors and meminductors[J]. Proceedings of the IEEE,2009,97（10）：1717-1724.

[3]Fitch A L,Iu H H C,Yu D S.Chaos in a memcapacitor based circuit[C].IEEE International Symposium on Circuits and Systems.IEEE,2014：482-485.

[4]Biolek D,Biolek Z,Biolkova V.SPICE modelling of memcapacitor[J].Electronics Letters,2010,46（7）：520-522.

[5]Yin Zhenyu,Tian Heng,Chen Guanhua,et al.What are memristor,memcapacitor,and meminductor[J].IEEE Transactions on Circuits&Systems II Express Briefs,2017,62（4）：402-406.

[6]Biolek D,Biolkova V.Mutator for transforming memristor into memcapacitor[J].Electronics Letters,2010,46（21）：1428-1429.

[7]Wang X Y,Fitch A L,Iu H H C,et al.Design of a memcapacitor emulator based on a memristor[J].Physics Letters A,2012,376（4）：394-399.

[8]Fouda M E,Khatib M A,Radwan A G.On the mathematical modeling of series and parallel memcapacitors[J].Microelectronics（ICM）,2013：1-4.

[9]Hu Zhiheng,Li Yingxiang,Jia Li,et al.Chaotic oscillator based on voltage-controlled memcapacitor[C].2010 International Conference on Circuits and Systems,2010：824-827.

[10]Fouda M E,Radwan A G.Boundary dynamics of memcapacitor in voltage-excited circuits and relaxation oscillators [J].Circuit Systems and Signal Processing,2015,34（9）：2765-2783.

[11]Fouda M E,Radwan A G..Resistive-less memcapacitorbased relaxation oscillator[J].International Journal of Circuit Theory and Applications,2015,43（7）：959-965.

[12]Popp P S,Herrmann J F,Fritz E C,et al.Impact of the nanoscale gap morphology on the plasmon coupling in asymmetric nanoparticle dimer antennas.Small,2016,12（12）：1667-1675.

[13]Yu D S,Zheng C Y,Iu H H C,et al.A memristive astable multivibrator based on 555 timer[C].2015 IEEE International Symposium on Circuits and Systems（ISCAS）,2015：858-861.

[14]Abuelma'atti M T,Khalifa Z J.A continuous-level memristor emulator and its application in a multivibrator circuit [J].Aeu-international Journal of Electronics and Communications,2015,69（4）：771-775.

[15]Chien H C.Three-mode controllable master-slave monostable multivibrators using current-feedback operational amplifiers[J].IET Circuits Devices and Systems,2014,8（6）：543-553.

[16]Lo Y K,Chien H C,Chiu H J.Switch-controllable OTRA-based bistable multivibrators[J].IET Circuits Devices and Systems,2008,2（4）：373-382.

[17]Yu Dongsheng,Liang Yan,Iu H H C,et al.A universal mutator for transformations among memristor,memcapacitor,and meminductor[J].IEEE Trans.Circuit and SystemsⅡ：Express Briefs,2014,61（10）：758-762.

[18]Yu D S,Liang Y,Chen H,et al.Design of a practical memcapacitor emulator without grounded restriction[J]. IEEE Transactions on Circuits and Systems,2013,60（4）：207-211.