锂离子电池建模与参数识别

刘 璇，王立欣，吕 超，李俊夫

（哈尔滨工业大学电气工程及自动化学院，哈尔滨150001）

锂离子电池能量密度高、输出功率大，越来越多地应用在新能源汽车、新能源发电等领域[1]。电池的广泛应用也对管理系统提出了更高的要求。对电池性能状态进行科学准确的估计和预测，以便让锂离子电池最大限度地释放电能发挥作用、长期稳定可靠地工作，需要构建一种准确、便捷、通用性好的模型。

将模型应用于管理系统当中，不仅要考虑模型的准确性，使模型尽量准确地还原电池的工作情况，还要考虑模型的简便程度，以使模型的计算合理占用资源提高效率[2]。目前，锂离子电池机理模型鲜见于实际系统中，主要由于描述电池内部复杂的物理、化学过程，通常形式复杂、计算耗时。常用的等效电路模型结构简单，但其参数无实际物理意义，对电池健康状态评估时意义不明确[3]。所以，有必要将电池电化学机理与等效电路模型相结合。

本文首先从锂离子电池的电化学机理出发，增加了热行为描述，提出了一种新的等效电路模型，然后利用激励响应分析的方法进行参数获取，最后通过仿真实验验证该模型的正确性和准确度。

1 等效电路模型

结合锂离子电池机理过程，本文提出一个等效电路模型，如图1所示。有别于现有的等效电路模型，该模型涵盖了开路电势以及欧姆极化、反应极化和浓差极化三部分过电势的计算[4]，热行为的描述包括产热和热扩散计算[5]，是一种简化的计算方法。模型包括2个子模型，目标是实现任意负载电流下电池的端电压和表壳温度进行仿真计算。

图1 锂离子电池等效电路模型Fig.1 Equivalent circuit model of lithium-ion Battery

（1）开路电势是对电池基本过程的描述，决定了电池端电压曲线的基本形状，其精确估计是电池充放电行为准确把握的基础。电池的电动势为2个电极开路电势的差，在电化学模型中，固相粒子表面浓度决定了开路电势[6]，其计算公式为

式中：Up和Un为已知的正、负极开路电势函数曲线[7]；为 正、负极集流体边界处两活性粒子的固相最大锂离子浓度为表面锂离子浓度。 类似地，在等效电路模型中，开路电势可以看成是电池荷电状态（SOC）的函数。在本文模型中，定义SOC范围为1～0，对应电池从满充状态放电至2.5 V。开路电势的计算公式为

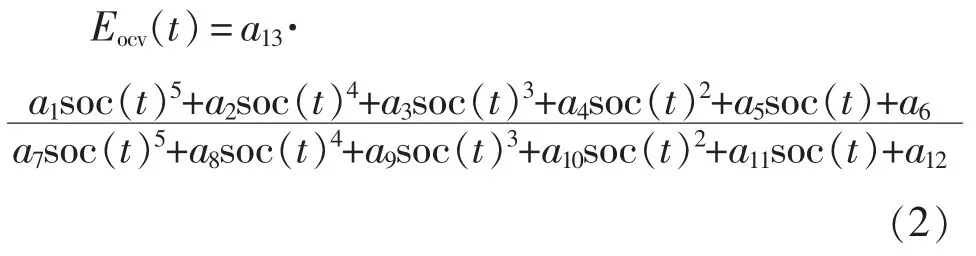
式中：a1～a13为拟合系数。SOC采用安时计数法[8]计算为

式中：I为负载电流，放电时为正；Qcapa为电池总放电容量。

（2）欧姆极化过电势与负载电流成正比，Rohm是用集中参数形式表达的电池欧姆内阻，则过电势与负载电流之间的函数关系为

（3）反应极化过电势表征了电池电化学反应过程，从其电化学阻抗谱曲线[9]可以看出，反应极化过电势的数值大小不仅与负载电流有关，也和电池SOC状态相关，即

式中，b1～b4为拟合系数

（4）浓差极化过程。在不考虑电池老化的情况下，根据物料守恒，固液相锂离子浓度总体保持平衡[6]。扩散的作用效果可以等效地看成是锂离子浓度差的建立过程，扩散过程由一个电容和电阻的组合形式来表示。为符合实际物理意义，设时间常数τ（τ=RconC）在电池各个状态时为固定值，初始时刻的 ηcon-polarization为 0， 则浓差极化过电势 ηcon-polarization的迭代计算公式为

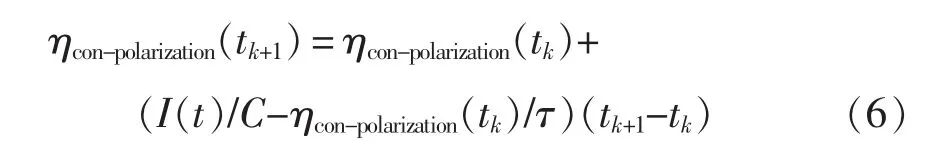
根据上述分析，可得电池端电压的计算公式为

热行为的描述包括产热和热扩散计算。电池内部温度沿径向分布的方程为

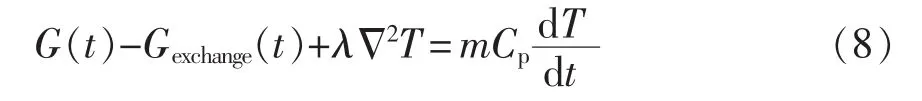
采用体积平均方法分析电池热行为[10]，认为电池是一个等温体，其温度的描述包括两个部分，内部温度和表面温度即用T和Tsurf来描述。电池输入的能量为自身产热G（t），借助热阻Rcond建立内部温度和电池表壳温度之间的函数关系[11]，即

规定Gexchange（t）为正值时，表示电池向环境放热，Gexchange（t）可表示为

由式（8）～式（10）可得

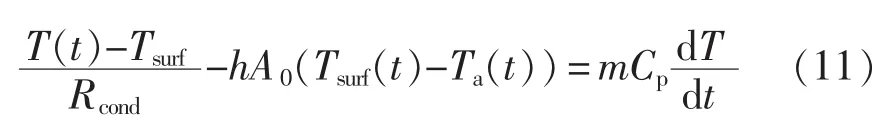
在假设条件下，热传导部分可以忽略不计[12]。简化的能量方程可以适用于各种形状的电池。则电池总产热G（t）计算公式为

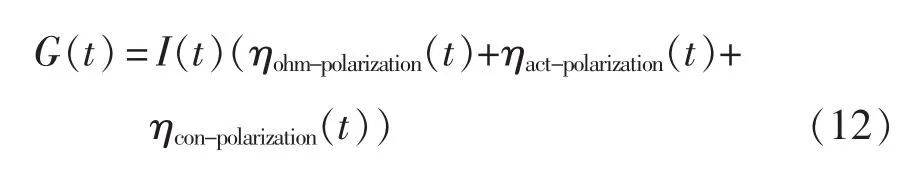
为计算电池内部温度和表面温度，将式（11）离散化可以得到

2 参数获取

良好的仿真精度和便捷的参数获取流程是衡量模型应用性的两个必要条件，如果模型只有高精度，参数获取过程复杂难以实现，那么便失去了模型的价值。除电池质量、电池表面积可由厂商提供或直接测量外，其他参数均需要估计。为此，对提出的模型进行分析，建立模型参数与端电压、表壳温度之间的数值函数关系，提出了基于激励响应分析的参数估计方法。

针对电池基本工作过程，实际中用较小倍率工况下测量的端电压近似为理想电动势曲线，即选择0.02C小倍率放电曲线作为电池理想电动势曲线[13]。使用最小二乘法拟合式（2），得到开路电势和SOC之间的函数关系。

电池内部各物理化学过程的时间常数不同，频率响应也不同。欧姆极化作用电子导电过程的响应最快，欧姆电阻导致的压降在施加电流激励后很短暂的时间即可产生，因此，可利用电化学阻抗谱的高频段测量电池的欧姆内阻。具体做法是电池静置后施加1 kHz正弦小电压激励，测量电池的电流响应，计算欧姆内阻。

反应极化过程需要设计动态工况用以辨识相应的参数。设计的动态负载电流、以及端电压和外壳温度响应曲线如图2所示，环境温度控制在25℃。

电流从0变化到某一固定值的瞬间，电压存在跳变ΔU，如图3所示。除去欧姆极化过电势，即为反应极化过电势。依据反应极化的计算式（5），使用最小二乘方法，拟合未知参数。

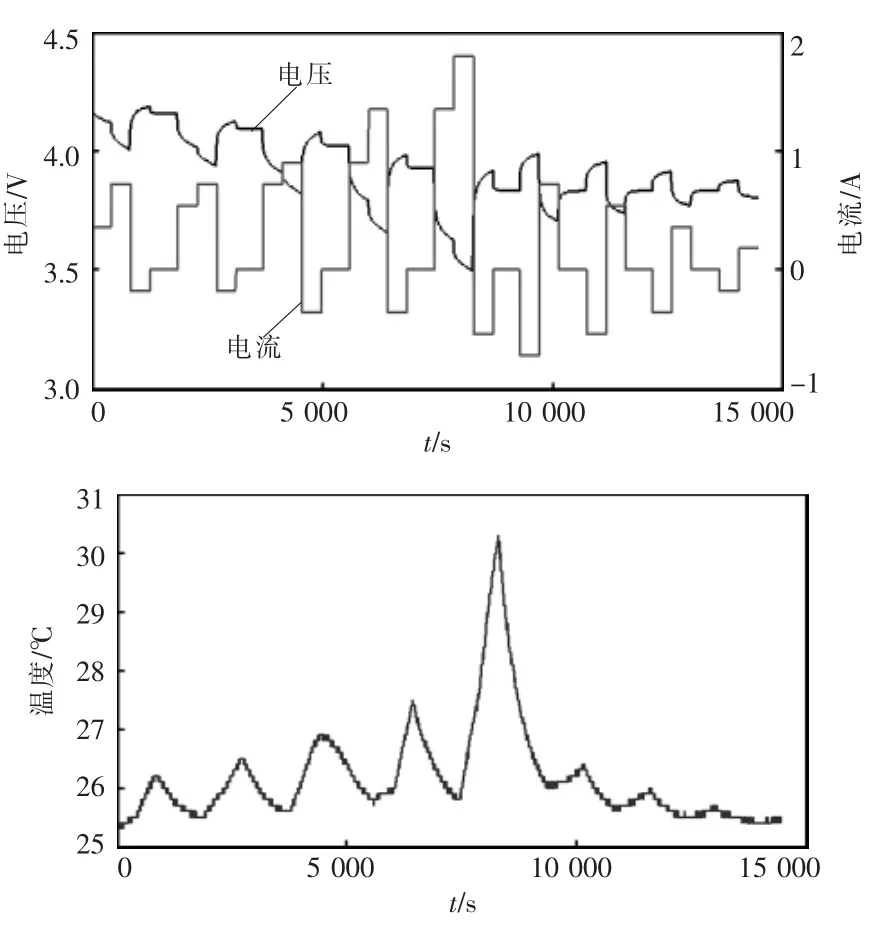
图2 负载电流、端电压和外壳温度动态响应曲线Fig.2 Dynamic response curves of load current,voltage and shell temperature

图3 负载电流及端电压动态响应细节曲线Fig.3 Dynamic response detail curves of load current and voltage

与上述情况不同，扩散过程需要一段过渡时间，才进入新的稳定状态，继而建立一个新的浓度差[14]。为了减小耗时，每段恒流充放电的时间控制为7 min。依据浓差极化过电势计算式（6），使用最小二乘方法，拟合未知参数。

在计算产热之前，需要设计工况辨识热容Cp。由式（11）可知，当负载电流为 0时，产热为 0，式（11）可变形为

认为电池表面温度和内部温度相等[15]，即当t=0时，T（0）=T0；当t=∞时，t（∞）=Ta。整理可得该方程的解析解为

电池的外壳温度与放电倍率和环境温度相关。图4给出了在不同的环境温度和不同倍率下，电池表壳温度的变化情况。在电池放电截止后，让其散热，恢复到室温，用式（16）进行拟合，得到的时间常数τheat取均值，进而计算Cp。

图4 电池表壳温度与放电倍率关系Fig.4 Relationship between surface temperature and discharge ratio of the battery

由于三部分过电势都与内部温度相关，如果过电势计算出现较大偏差，热行为的计算结果将出现较大误差。产热计算公式变为

能量平衡方程经整理可以写成

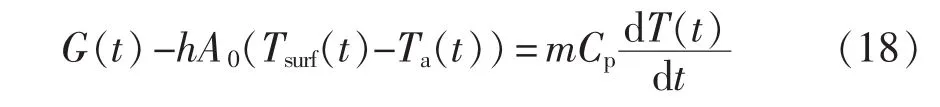
根据实测可以得到Uapp（t）和Tsurf（t），记

则热阻Rcond的计算公式为

3 参数估计验证

选取天津力神公司的LS.LR1865BC锂离子电池进行参数获取，该电池基本参数数据如表1所示，电池实验测试系统设备参数如表2所示。

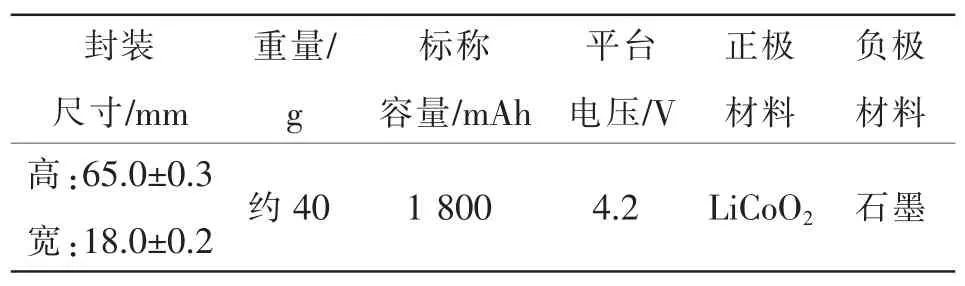
表1 LS.LR1865BC电池基本参数Tab.1 Basic parameters of LS.LR1865BC battery

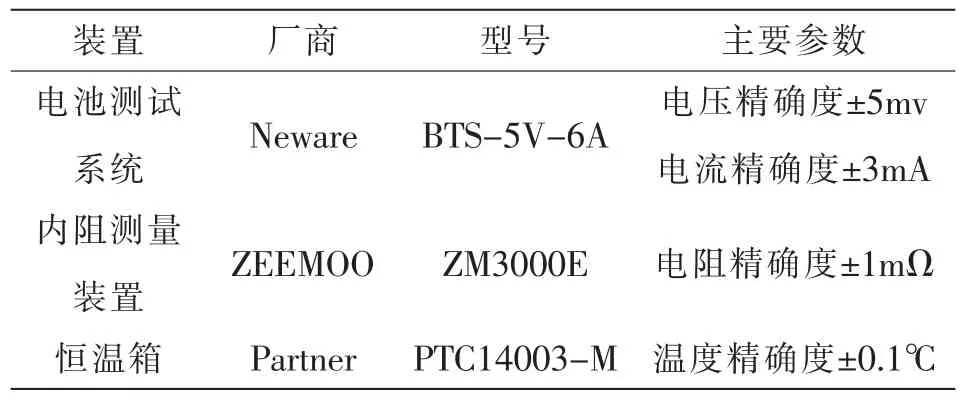
表2 电池实验测试系统设备参数Tab.2 Parameters of test system equipment of battery

对LS.LR1865BC锂离子电池进行参数辨识，根据辨识得到的参数，参照第2部分介绍的模型内容，计算电池端电压和表壳温度曲线，用辨识工况的数据进行验证。利用实验设备测量得到该节电池的端电压及表壳温度曲线，将仿真结果与实测结果进行对比，仿真结果如图5所示。同样地，随机选取多节不同型号的锂电池进行参数辨识与验证，仿真结果与实测结果均有较高的一致性。验证结果表明，提出的模型可以比较准确地仿真电池的行为。

在不同环境温度和动态负载电流下，电池充放电行为的仿真和实测对比结果如图6所示，误差结果如表3所示。从仿真结果可以看出，由于忽略了电池正负极材料熵系数给产热计算带来的影响，外壳温度计算并未出现最大局部温度。电压的仿真计算在室温附近时，比较精确。当环境温度大于40℃或者低于20℃时，端电压的计算会有较大误差。这是因为模型中，开路电势和过电势的计算并未考虑温度对其影响[18]，这也是今后将重点研究的内容。

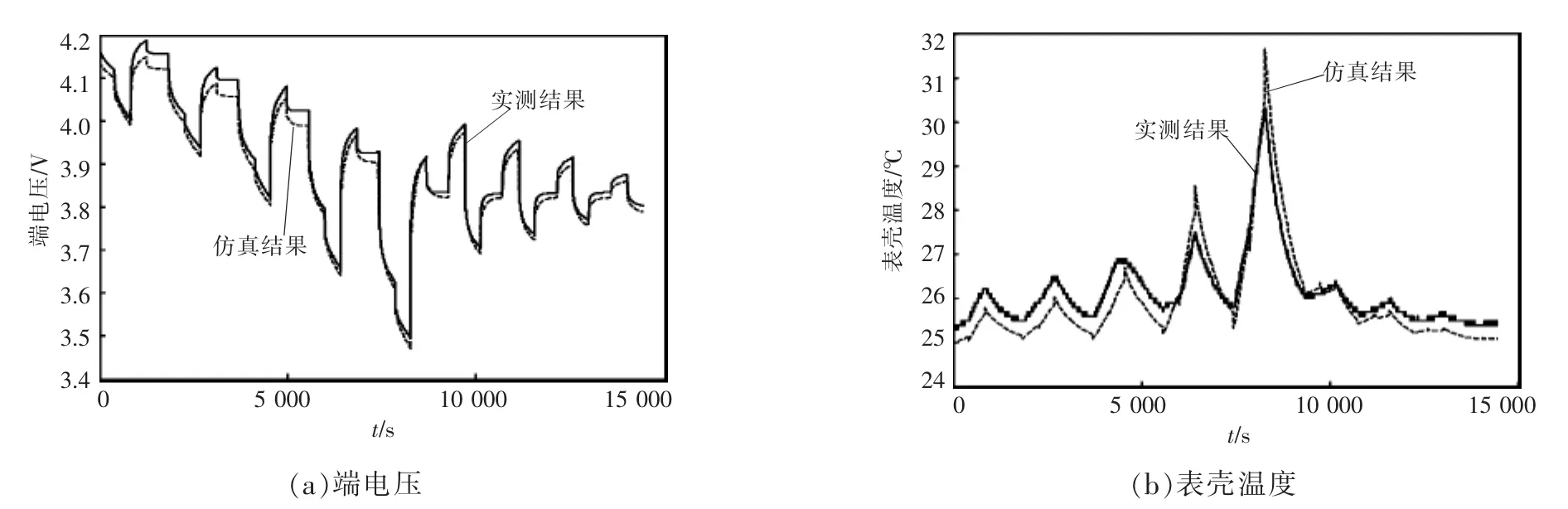
图5 电池端电压和表壳温度的仿真与实测曲线Fig.5 Simulation and measured curves of battery voltage and surface temperature

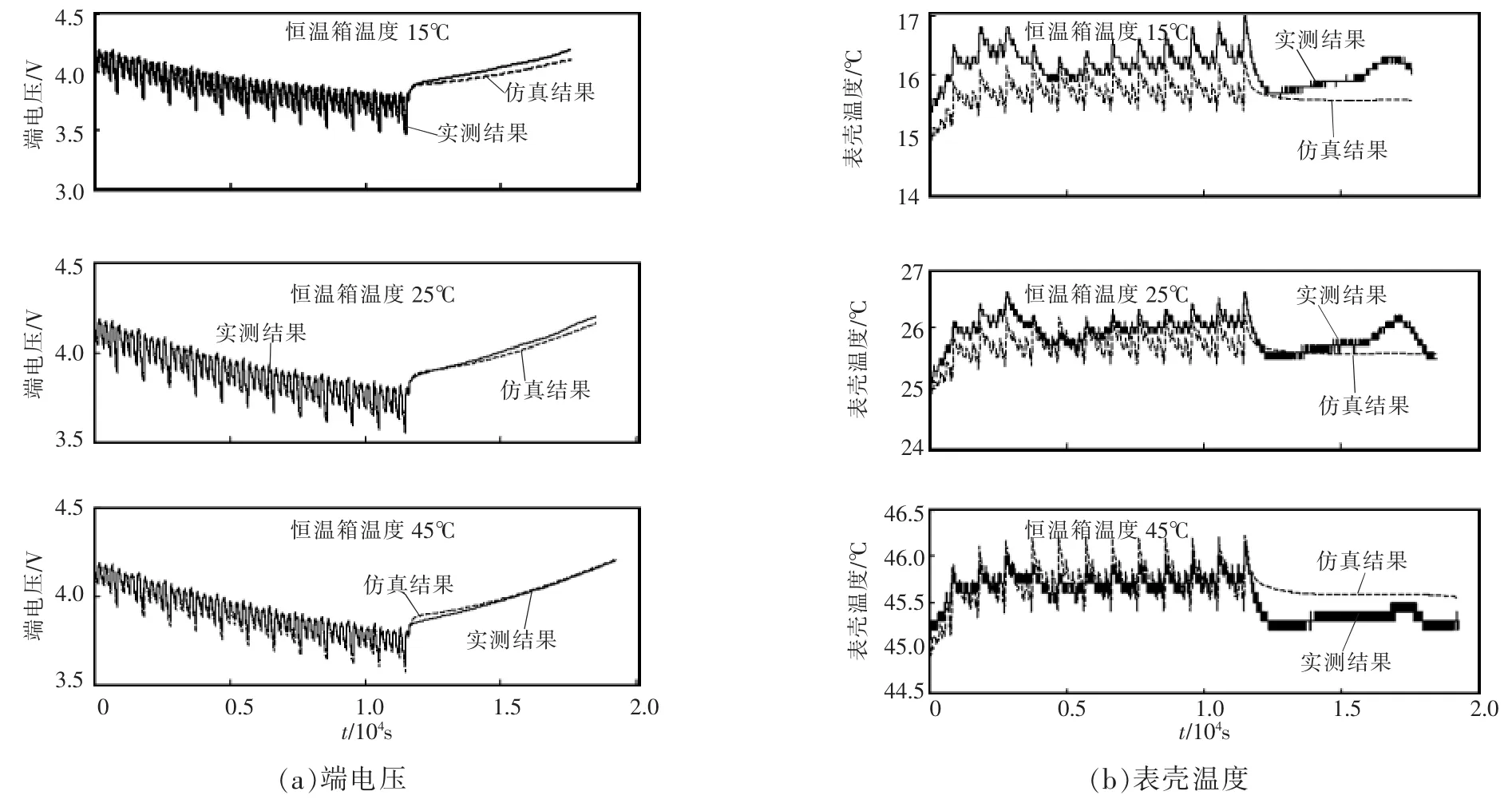
图6 电池充放电行为的仿真和实测对比结果Fig.6 Simulation and measured comparison results of battery charging and discharging behavior

表3 动态负载电流下仿真和实测结果误差Tab.3 Simulation and measured error of dynamic load current

4 结语

本文结合电池机理，提出了一种等效电路模型，设计不同辨识工况来获取模型中的参数，并给出了在不同的恒定环境温度下，对任意负载电流的端电压和表壳温度的仿真计算。验证结果表明，在室温附近或室温以上，模型具有很好的适用性。该研究为机理模型应用于电池管理系统提供了一定的技术支持，为解决电池管理系统精度不高、性能描述不全面的问题提供了解决思路。

[1]Hu Xiaosong,Li Shengbo,Peng H.A comparative study of equivalent circuit models for Li-ion batteries[J].Journal of Power Sources,2012,198（2）：359-367.

[2]Doyle M,Fuller T F,Newman J.Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell [J].Journal of the Electrochemical Society,1993,140（6）：1526-1533.

[3]Rahimian S K,Rayman S,White R E.Comparison of single particle and equivalent circuit analog models for a lithiumion cell[J].Journal of Power Sources,2011,196（20）：8450-8462.

[4]Haran B S,Popov B N,White R E.Determination of the hydrogen diffusion coefficient in metal hydrides by impedance spectroscopy[J].Journal of Power Sources,1998,75（1）：56-63.

[5]Guo M,Sikha G,White R E.Single-particle model for a lithium-ion cell：Thermal behavior[J].Journal of the Electrochemical Society,2011,158（2）：A122-A132.

[6]Schmidt A P,Bitzer M,Imre ÁW,et al.Experiment-driven electrochemical modeling and systematic parameterization for a lithium-ion battery cell[J].Journal of Power Sources, 2010,195（15）：5071-5080.

[7]Luo Weilin,Lü Chao,Wang Lixin,et al.An approximate solution for electrolyte concentration distribution in physics-based lithium-ion cell models[J].Microelectronics Reliability,2013,53（6）：797-804.

[8]Tatsukawa E,Tamura K.Activity correction on electrochemical reaction and diffusion in lithium intercalation electrodes for discharge/charge simulation by single particle model[J].Electrochimica Acta,2014,115（4）：75-85.

[9]Baba N,Yoshida H,Nagaoka M,et al.Numerical simulation of thermal behavior of lithium-ion secondary batteries using the enhanced single particle model[J].Journal of Power Sources,2014,252（15）：214-228.

[10]Eddahech A,Briat O,Vinassa J M.Thermal characterization of a high-power lithium-ion battery：Potentiometric and calorimetric measurement of entropy changes[J].Energy,2013,61（6）：432-439.

[11]Forgez C,Do D V,Friedrich G,et al.Thermal modeling of a cylindrical LiFePO 4/graphite lithium-ion battery[J]. Journal of Power Sources,2010,195（9）：2961-2968.

[12]Zhang Jianbo,Ge Hao,Li Zhe,et al.Internal heating of lithium-ion batteries using alternating current based on the heat generation model in frequency domain[J].Journal of Power Sources,2015,273（7）：1030-1037.

[13]Saito Y,Shikano M,Kobayashi H.Heat generation behavior during charging and discharging of lithium-ion batteries after long-time storage[J].Journal of Power Sources,2013, 244（4）：294-299.

[14]Vazquez-Arenas J,Gimenez L E,Fowler M,et al.A rapid estimation and sensitivity analysis of parameters describing the behavior of commercial Li-ion batteries including thermal analysis[J].Energy Conversion and Management,2014, 87（15）：472-482.

[15]Tourani A,White P,Ivey P.A multi scale multi-dimensional thermo electrochemical modelling of high capacity lithium-ion cells[J].Journal of Power Sources,2014,255（6）：360-367.

[16]Li Junfu,Wang Lixin,Lü Chao,et al.New method for parameter estimation of an electrochemical-thermal coupling model for LiCoO2 battery[J].Journal of Power Sources,2016, 307（9）：220-230.

[17]Luo Weilin,Lü Chao,Wang Lixin,et al.A new extension of physics-based single particle model for higher chargedischarge rates[J].Journal of Power Sources,2013,241（1）：295-310.

[18]吕超,郑君,罗伟林,等.锂离子电池热耦合SP+模型及其参数化简[J].电源学报,2015,13（3）：28-35. Lü Chao,Zheng Jun,Luo Weilin,et al.Thermal coupling SP+model of lithium-ion battery and parameters simplification[J].Journal of Power Supply,2015,13（3）：28-35（in Chinese）.