计及间谐波的电动汽车快速充电装置电能计量

高敬更，王兴贵

（兰州理工大学电气工程与信息工程学院，兰州730050）

电动汽车作为一种新能源交通工具已成为汽车工业发展的必然趋势。大规模电动汽车接入电网，一方面对电力系统负荷增长和系统稳定性带来了挑战；另一方面对提高电力系统设备利用率和电能消费占终端能源消费比重带来了新的机遇[1-2]。电动汽车通过充电装置为蓄电池充电，其工作方式分为慢速充电和快速充电两种模式。慢速充电时充电电流为15 A左右，充电时间一般要4～5 h；快速充电时充电电流为100～500 A[3]，输出电压为200～750 V，充电时间为20 min～2 h。

电动汽车充电装置由整流电路、功率变换电路等非线性电力电子元器件组成，作为非线性负荷，电动汽车充电装置对电能计量造成的失准问题受到广泛关注。文献[4]指出在快速充电时，充电装置作为大功率、非线性的新型谐波源，其产生的谐波电流将注入公用电网，导致供电系统的电能质量降低；文献[5-8]针对充电站对电网的谐波污染问题，设计了充电机谐波测量模型，并对数据进行了对比分析，用实测数据得出结论：充电站接入会对电网运行产生影响，需从多方面采取措施。2009年出台的 《电动汽车非车载充放电机通用技术要求》（Q/ GDW 397-2009）规定了充放电机向电网注入的直流电流、谐波和波形畸变率等参数要求；2010年出台的《电动汽车充电系统技术规范第3部分：非车载充电机》（Q/GDW 397-2009）规定了高频开关电源模块2～25次谐波电流含有率和交流输入电压畸变率等参数要求。上述文献研究了谐波对电网影响，但未分析充电装置谐波、间谐波的波形畸变对电能计量装置准确度的影响，由于这些计量装置大多按工频正弦运行工况设计[9]，波形畸变必然使电能计量结果失准，将直接关系到电力供需双方的经济效益。

按照常用的全电能计量方式，即直接按电能定义式将时域电压电流信号采样值相乘后积分来计算电能，会导致快速充电装置在污染电网的同时，少计间谐波电能。本文基于广义dk-qk坐标变换理论，研究了一种计及间谐波检测的电能计量方法，分别计量基波电能、谐波电能和间谐波电能，使电能计量更加准确、公平[10]。

1 充电装置谐波和间谐波功率特性

充电装置作为谐波源[11-13]，在吸收有功功率的同时，会将其中一部分功率转化为谐波和间谐波，注入系统，从而引起网侧的电压与电流畸变，功率流向如图1所示，。反送的谐波功率和间谐波功率与基波功率方向相反，从而使得充电装置电能测量点处的总有功功率小于基波有功功率。

基波有功功率平衡方程式为

式中：Pn为第n个充电装置消耗的基波功率；n为整数；PS为线路阻抗消耗的功率。

图1 功率流向Fig.1 Power flow

谐波和间谐波功率平衡方程式为

式中：Pkn为第n个充电桩产生的k次谐波功率或间谐波功率；Pks为线路阻抗消耗的k次谐波或间谐波功率；k为整数或非整数。

2 谐波功率和间谐波功率的计算

本文采用基于瞬时无功功率理论，从坐标变换的数学角度研究基于广义 dk-qk旋转坐标变换[14-17]的计量方法，能够快速准确地区分电动汽车充电装置产生任意k次谐波和间谐波参数，用二阶butter worth低通滤波器提取信号进行反变换，从而实现基波电能、谐波电能和间谐波电能的分别计量，并消除模拟滤波器的相位问题，避免对有些频率分量的增大或衰减。

2.1 基于广义dk-qk的谐波和间谐波参数检测

在三相对称电力系统中，电压和电流交流量由基波含量、谐波含量和间谐波含量组成[18]，其数学表达式分别为

式中：fa、fb、fc分别为a、b、c三相交流量（电压/电流）；F为交流量的有效值；m为正整数；h为非正整数；φm和φh分别为m次谐波和h次间谐波分量的初始相位角。

若待检测的谐波为k次，则广义dk-qk坐标变换在dk-qk坐标系统中以角频率kωt进行旋转，如图2所示。

图2 广义dk-qk坐标变换Fig.2 Generalized dk-qkcoordinate transformation

广义dk-qk坐标变换系与abc三相坐标系变换矩阵为

通过改变广义dk-qk坐标变换矩阵中的k，当k为已知量且为正整数，应用广义dk-qk坐标变换对h次谐波进行检测，则得

当k=h时，对于待检测的h次间谐波可得

此时h次间谐波为直流分量，其他次谐波分量依然为交流量，通过合理设定二阶butter worth低通滤波器参数，将h次直流分量f¯dk和f¯qk滤出。

再通过广义dk-qk坐标反变换，还原h次间谐波到abc坐标系下，即

当k为已知量且为正整数时，同理根据式（3）～式（8），对检测到的m次谐波分量采用上述方法进行反变换还原到abc坐标系下，得m次间谐波电压/电流交流量，即

2.2 谐波和间谐波的电能计量方法

根据广义dk-qk坐标变换反变换的结果式（8）和式（9），测得电压、电流交流量值，按照美国电气与电子工程师协会（IEEE）于2010年颁布的IEEE 1459标准中有关非正弦信号的定义[19]，则有

式中：ω为基波角频率；Uk、Ik分别为k次电压、电流频率分量有效值；αk、βk分别为k次电压、电流频率含量的相角。

根据有功功率定义及三角函数的正交性，同频率的电压和电流才构成有功功率，而不同频率的电压和电流并不构成有功功率，即有功功率P（t）为

上述电压电流交流量产生的有功电能为

式中：W1为基波有功电能；Wm为m次谐波有功电能；Wh为h次间谐波有功电能。谐波和间谐波的有功电能计量如图3所示。

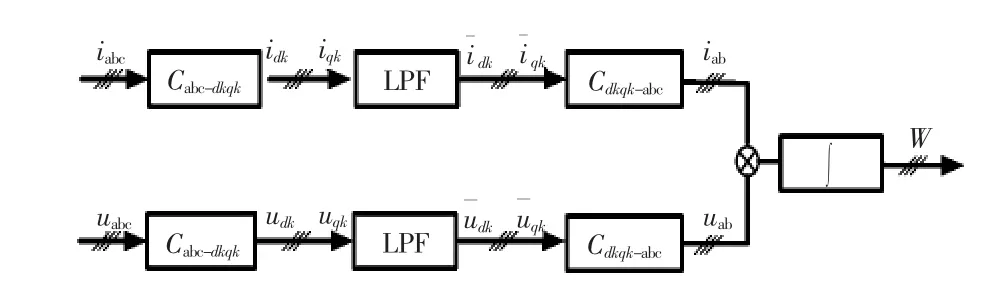
图3 谐波和间谐波电能计量原理Fig.3 Schematic of electric energy metering for harmonics and inter-harmonics

3 充电装置仿真模型

根据充电装置工作原理设计谐波和间谐波测量系统模型[20-23]，电源采用 10 kV电压，变压器为10/0.4 kV电压等级，dyn11接法，电感电容采用常见的充电装置参数，如表1所示。

为了便于仿真，可将充电装置功率变换环节进行等效。快速充电装置的工作时间相对于工频周期而言比较长，在一个至几个工频周期内，可认为快速充电装置的输出电流和输出电压是恒定的直流，工作在恒功率状态，即用一个非线性电阻RC来近似模拟功率变换环节的等效输入电阻。RC可近似表示为

表1 充电装置参数Tab.1 Parameters of charging parameter

式中：UB、I1、P1分别为功率变换电路的输入电压、电流、功率；UO、IO、PO为功率变换电路的输出电压、电流、功率；η为功率模块变换效率。

RC值随充电装置输出功率变化如图4所示。

本文在Matlab/Simulink环境下建立的充电装置等效仿真模型如图5所示，充电装置均设置同一参数。设定采样频频率fs=10.24 kHz，采样点数N= 2 048（对应于10个基波周期内的采样点数）[10]，其中仿真测量数据采用国标规定的测量方法，即取测量时段内各相测量值的95%概率值。

图4 等效输入电阻RCFig.4 Equivalent input resistances of RC

图5 充电装置仿真模型Fig.5 Simulation model of charging device

4 计及间谐波的电能计量仿真分析

快速充电装置由非线性电力电子元件组成，其产生的谐波和间谐波注入电网侧，引起电网侧电压电流波形畸变。额定功率为180 kW的充电装置，其电网侧电流波形如图6所示，测得电网侧谐波电压总畸变率为2.89%、谐波电流总畸变率为27.85%；重复3次测得有功功率为184.9 kW，视在功率190.6 kW，计算得功率因数为0.97。

图6 电网侧电流波形Fig.6 Waveforms of grid power current

基于广义dk-qk坐标变换对特定次谐波进行检测并分析，检测到的基波频率附近55 Hz，65 Hz，75 Hz及85 Hz的特定次谐波波形如图7所示。

从图7可以看出，采用广义dk-qk坐标变换对特定次间谐波的检测，检测到的波形与上述分析一致。检测到各频率间谐波相电流有效值：55 Hz为0.50 A，65 Hz为0.45 A，75 Hz为0.47 A，85 Hz为0.43 A，95 Hz为0.37 A，各频率间谐波电流有效值呈下降趋势，随频率增高而减小；各频率间谐波电流含有率：55 Hz为0.14%，65 Hz为0.13%，75 Hz为0.13%，85 Hz为0.12%，95 Hz为0.10%，各频率间谐波电流含有率也呈下降趋势，随频率增高而减小。

图7 特定次间谐波波形Fig.7 Waveforms of specific inter-harmonics

4.1 额定功率下有功功率特性分析

采用广义 dk-qk坐标变换对额定功率为 180 kW充电装置特定次间谐波和谐波有功功率进行检测，其有功功率如表2所示。

表2 基波背景下间谐波和谐波有功功率Tab.2 Active powers of inter-harmonics and harmonics based on fundamental wave

对表2数据进行分析，除了谐波有功功率在250 Hz较大外，谐波和间谐波有功功率总体呈递减状态，有功功率随着频率增高，其值越来越小；在100 Hz之内，间谐波有功功率相对较大，在95 Hz为2.742 W，而谐波功率在650 Hz为2.681 W。

分别对5台、10台、20台，40台同一型号额定功率为180 kW的充电装置的间谐波和谐波有功功率进行检测，其间谐波和谐波占基波有功功率比重如图8和图9所示。

从图8和图9可以看出，随着频率的增高，间谐波的有功功率占基波有功功率比重呈递减趋势；间谐波功率在基波频率附近占比重较高，55 Hz为0.011%，在95 Hz以后比重在0.001%以下。间谐波的有功功率占基波有功功率比重在频率250 Hz处最大，之后随频率增高而减小，250 Hz为0.031%，在650 Hz以后其比重在0.001%以下。随着充电装置台数的增加，谐波和间谐波所占比重基本不变。

图8 间谐波有功功率占基波有功功率比重Fig.8 Active power ratio between inter-harmonics and fundamental wave

图9 谐波有功功率占基波功率比重Fig.9 Active power ratio between harmonics and fundamental wave

4.2 输出功率变化时有功功率特性分析

在充电装置输出功率分别为40、80、120、180和240 kW情况下，检测特定次谐波和间谐波的有功功率，结果如图10和图11所示。

从图10可以看出，间谐波有功功率随频率增高而减小，离基波频率越近，其有功功率越大；并随充电桩装置输出功率增大而增大，在充电装置输出功率为240 kW时，55 Hz间谐波有功功率为32 W，而95 Hz间谐波有功功率为3 W。

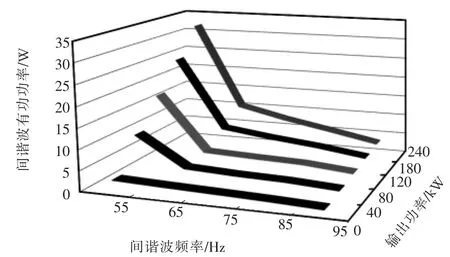
图10 间谐波有功功率特性变化Fig.10 Changing characteristics of inter-harmonics active power

图11 谐波有功功率特性变化Fig.11 Changing characteristics of harmonics active power

由图11可以看出，在充电装置输出功率为240 kW时，150 Hz谐波有功功率为60.45 W，250 Hz谐波有功功率为75.57 W，650 Hz谐波有功功率为3 W。谐波有功功率在频率250 Hz处最大，之后随频率增高而减小；并随充电桩装置输出功率增大而增大。

根据上述充电装置的谐波和间谐波有功功率特性，其产生的3、5、7、9、11和13次谐波有功功率较大，且频段比较长。在低频100 Hz以内，间谐波大量存在，间谐波频率离基波频率越近，其有功功率越大，但频段比较短。

5 结语

本文在电动汽车充电装置快速充电工况下，分析了其谐波和间谐波功率特性对计量影响，研究了一种基于广义dk-qk坐标变换的计及间谐波电能计量方法。通过广义dk-qk坐标变换，把待检测的任意k次谐波和间谐波变换为直流量，通过合理设定二阶butter worth低通滤波器参数将直流分量和滤出；再通过坐标反变换，测得任意k次谐波和间谐波电压/电流交流量，通过计算出任意k次谐波电能及间谐波电能，实现任意k次基波、谐波和间谐波分开计量，与全电能计量方式相比降低了电能计量误差。

分析了充电装置在额定功率下有功功率特性和输出功率变化时有功功率的特性。仿真实验结果表明：基于广义dk-qk坐标变换的计及间谐波电能计量方法是可行性的。同时该方法也为谐波和间谐波治理和合理计量提供了理论依据。

[1]陈滋健.基于风光互补综合供电的电动汽车充电站[J].电源学报,2013,11（1）：129-132.

Chen Zijian．EV charging station based on the comprehensive power supply of hybrid wind/photovoltaic[J].Journal of Power Supply,2013,11（1）：129-132（in Chinese）．

[2]时培成,刘刚,孙阳敏,等.基于发电能耗折算的电动汽车节能分析[J].电源学报,2014,12（5）：56-59．Shi Peicheng,Liu Gang,Sun Yangmin,et al.Analysis of electric vehicle energy conservation basedon power generation energy consumption[J].Journal of Power Supply,2014, 12（5）：56-59（in Chinese）.

[3]高赐威,吴茜.电动汽车换电模式研究综述[J].电网技术, 2013,37（4）：891-898. Gao Ciwei,Wu Xi.A survey on battery-swapping mode of electric vehicle[J].Power System Technology,2013,37（4）：891-898（in Chinese）.

[4]王辉,粟梅,孙尧,等.应用于V2G的AC/DC矩阵变换器[J].中国电机工程学报,2013,33（9）：34-41.

Wang Hui,Su Mei,Sun Yao,et al.AC/DC matrix converters for V2G applications[J].Proceedings of the CSEE,2013,33（9）：34-41（in Chinese）.

[5]朱学贵,覃阳,苏向丰,等.电动汽车充电机对电能计量的影响[J].电力自动化设备,2015,35（6）：52-57.

Zhu Xuegui,Tan Yang,Su Xiangfeng,et al.Im pact of electric vehicle charger on electric energy metering[J]. Electric Power Automation Equipment,2015,35（6）：52-57（in Chinese）.

[6]高赐威,张亮.电动汽车充电对电网影响的综述[J].电网技术,2011,35（2）：127-131.

Gao Ciwei,Zhang Liang.A survey of influence of electrics vehicle charging on power grid[J].Power System Technology,2011,35（2）：127-131（in Chinese）.

[7]陈新琪,李鹏,胡文堂,等.电动汽车充电站对电网谐波的影响分析[J].中国电力,2008,41（9）：31-36.

Chen Xinqi,Li Peng,Hu Wentang,et al.Analysis of impacts of electric vehicle charger on power grid harmonic[J]. Electric Power,2008,41（9）：31-36（in Chinese）.

[8]赵伟,姜飞,涂春鸣,等.电动汽车充电站入网谐波分析[J].电力自动化设备,2014,34（11）：61-66.

Zhao Wei,Jiang Fei,Tu Chunming,et al.Harmonic currents of grid-connected EV charging station[J].Electric Power Automation Equipment,2014,34（11）：61-66（in Chinese）.

[9]李斌勤,陈伟根,李刚.谐波对电网中有功计量装置的影响[J].电网技术,2010,34（6）：154-159.

Li Binqin,Chen Weigen,Li Gang.Analysis on effects of harmonic active energy metering devices[J].Power System Technology,2010,34（6）：154-159（in Chinese）.

[10]徐文佳,赵伟,黄洪涛,等.计及间谐波的电能计量方法[J].电网技术,2016,40（2）：657-662.

Xu Wenjia,Zhao Wei,Huang Hongtao,et al.A method for electrical energy measurement in consideration of interharmonics[J].Power System Technology,2016,40（2）：657-662（in Chinese）.

[11]宁志毫,罗隆福.大功率整流系统谐波功率特性及其对电能计量的影响和节能分析[J].电工技术学报,2012,27（11）：248-255.

Ning Zhihao,Luo Longfu.Analysis of energy saving and harmonic power characteristics and its effects on electric energy measurement in high power rectifier system[J]. Transactions of China Electrotechnical Society,2012,27（11）：248-255（in Chinese）.

[12]刘峰.基于小波变换的电力系统谐波电能计量研究[J].沈阳工程学院学报,2011,7（2）：138-141.

Liu Feng.Power system harmonic energy metering based on wavelet transform[J].Journal of Shenyang Institute of Engineering,2011,7（2）：138-141（in Chinese）.

[13]申邵东,魏星.谐波对有功电能计量影响的仿真研究[J].电力自动化设备,2008,28（2）：54-56.

Shen Shaodong,Wei Xing.Influence of harmonics on electric energy measurement[J].Electric Power Automation Equipment,2008,28（2）：54-56（in Chinese）.

[14]印海文,牟龙华.一种基于d-q-0坐标变换的频率测量算法[J].电力系统保护与控制,2011,39（12）：79-83.

Yin Haiwen,Mou Longhua.A frequency measuring algorithm based on d-q-0 transformation[J].Power System Protection and Control,2011,39（12）：79-83（in Chinese）.

[15]周伟,牟龙华.一种基于αβ与dq坐标变换的频率检测算法[J].电力系统保护与控制,2012,40（1）：62-67.

Zhou Wei,Mou Longhua.A frequency detection algorithm based on αβ and dq coordinate transformation[J].Power System Protection and Control,2012,40（1）：62-67（in Chinese）.

[16]张波,易颂文,何晓敏,等.基于广义dk-qk旋转坐标变换的谐波电流检测方法[J].电力系统及其自动化学报,2001, 13（3）：25-29.

Zhang Bo.A harmonic current detection method based on a generalized dk-qk coordinate transform[J].Proceedings of the EPSA,2001,13（3）：25-29（in Chinese）.

[17]谢锐凯,张波.整数次谐波、间谐波综合检测原理和装置[J].电气应用,2007,26（10）：83-87.

Xie Ruikai,Zhang Bo.Integrated detection principle and device for integer harmonics and inter-harmonics[J].Electrotechnical Application,2007,26（10）：83-87（in Chinese）. [18]Xie Ruikai.Zhang Bo,Qiu Dongyuan,et al.An inter-harmonic detecting algorithm based on the generalized dk-qk coordinate transform[C].In IEEE 38th Annual Power Electronics Specialists Conference,Orlando,2007：1126-1131.

[19]IEEE Std 1459-2010.IEEE standard definitions for the measurement of electric power quantities under sinusoidal, non-sinusoidal,balanced,or underbal anced conditions-Redline[S].IEEE,2010：1-52.

[20]张谦,韩维健,俞集辉,等.电动汽车充电站仿真模型及其对电网谐波影响[J].电工技术学报,2012,27（2）：159-164.

Zhan Qian,Han Weijian,Yujihui,et al.Simulation model of electric vehiclecharing station and the harmonic analysis on power grid[J].Transactions of China Electrotechnical Society,2012,27（2）：159-164（in Chinese）.

[21]黄梅,黄少芳.电动汽车充电站谐波的工程计算方法[J].电网技术,2008,32（20）：20-23.

Huang Mei,Huang Shaofang.A harmonic engineering calculation method for electric vehicle charging station[J]. Power System Technology,2008,32（20）：20-23（in Chinese）.

[22]李娜,黄梅.不同类型电动汽车充电机接入后电力系统的谐波分析[J].电网技术,2011,35（1）：170-174.

Li Na,Huang Mei.Analysis on harmonics caused by connecting different types of electric vehicle charger with power network[J].Power System Technology,2011,35（1）：170-174（in Chinese）.

[23]黄梅,黄少芳,姜久春.电动汽车充电机（站）接入电力系统的谐波分析[J].北京交通大学学报,2008,32（5）：85-88.

Huang Mei,Huang Shaofang,Jiang Jiuchun.Harmonic study of electric vehicle chargers[J].Journal of Beijing Jiaotong University,2008,32（5）：85-88（in Chinese）.