基于储能运行策略的孤岛型微网可靠性分析

王玉梅，吴志明

（河南理工大学电气工程与自动化学院，焦作454000）

近年来，国内外学者主要研究分布式电源和并网型微网的供电可靠性，对孤岛型微网研究较少。孤岛型微网建设在偏远地区或海岛上，具有独立组网、高度自治的特点[1]，储能作为孤岛型微网重要的组成部分，其运行策略及充放电过程直接影响着系统运行，在可靠性评估时也须计及储能设备的运行策略对微网可靠性的影响[2]。文献[1]采用故障树图法对孤岛运行的微网持续供电能力进行了分析，但忽视了分布式电源输出的随机不可控性对可靠性的影响；文献[3-4]对含分布式电源的配电网可靠性分析均采用了解析法，但未考虑到分布式电源输出的时序特性；文献[5]在进行可靠性评估时建立了并网型微网孤岛运行全时序可靠性模型，但忽略了储能策略对微网系统可靠性的影响；文献[6]运用蒙特卡洛法分析了含微网的配电网的可靠性评估指标，但对孤岛运行微网功率输出不足时，内部负荷的切除顺序未做分析；文献[7-8]研究了储能不同运行策略下的负荷切除原则，但仅分析了基于孤岛运行特性的风储微网的可靠性，忽略了风光储互补发电系统弥补风储独立发电在资源上利用的不足[3,9]。为此，本文进行了储能孤岛型微网可靠性分析。

1 孤岛型微网可靠性评估模型

孤岛型微网长期脱离配电网运行，负荷仅依靠内部电源供电，一般包括分布式等新能源发电和储能系统。

1.1 电源功率输出模型

1.1.1 光伏电源功率输出随机模型

1）光强概率模型

通过对实际光强概率分布进行函数拟合得到光强Beta[10-11]分布模型，其概率密度函数f（x）为

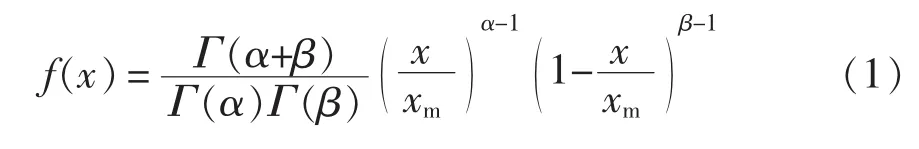
式中：xm和x分别为模拟时间内的最大光强和实际光强，W/m；Γ为Gamma函数；α和β分别为Beta分布的形状参数，α和β表达式[12]通常根据模拟时间内光强的平均值和方差确定。

2）光伏电源功率输出随机模型

若一个光伏电池方阵由N个电池组件组成，其中每个组件的光电转换效率和面积分别为 ηn和An，则对应的输出功率为

式中：A为方阵面积；η为方阵光电转换效率。

由式（1）、式（2）得到光伏电源功率输出概率分布函数为

1.1.2 风电机组功率输出随机模型

1）风速Weibull分布模型

风速Weibull分布模型是在历史测量数据基础上进行函数拟合得到的，其分布函数和概率密度函数分别为[13]

式中：v为实际风速；k和c分别为形状参数和尺度参数，可用参数估计法[14]确定。

2）风电机组功率输出随机模型

风电机组WTG（wind turbine generator）的运行方式导致WTG功率输出随风速变化，通常采取分段函数来描述其功率输出P和风速V之间的变化规律，如图1所示。其表达式为

式中：Pr和Vr分别为风电机组的额定功率和额定风速；Vci和Vco分别为风机的切入和切出风速；参数A、B、C分别为关于Vci、Vco、Vr的函数，表示为

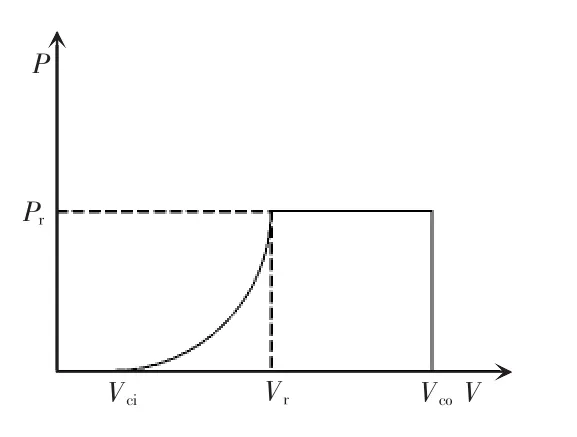
图1 风电机组功率特性曲线Fig.1 Characteristics curve of wind turbine generator WTG power

1.2 储能系统模型

储能系统作为孤岛型微网重要组成部分，通常和分布式电源一起给微网内部负荷供电[15]，不仅能平滑分布式电源输出功率的不稳定，还能提高配电网供电可靠性并改善电能质量。综合考虑储能的容量和最大充放电约束，分别建立储能充、放电模型。

充电模型为

放电模型为

式中：Pbat（t）和Vbat（t）为t时刻储能充放电功率和存储的容量；Pdch-max和Pch-max为储能最大放电和最大充电功率；Vin、Vout为储能充、放电容量；Vmax、Vmin为储能最大、最小容量约束；Top为孤岛运行储能充电、放电时间。

2 孤岛型微网负荷切除原则

2.1 孤岛型微网全时序运行状态

孤岛型微网负荷仅由网内分布式电源和储能系统共同协调供电[16-17]。运行状态全时序分析如表1所示。表中PSUM、Pbat、PL分别表示分布式电源（光伏电源和风电机组）的功率输出总和、储能装置输出和负荷需求。

表1 孤岛型微网运行全时序状态分析Tab.1 State analysis of total sequence of isolated island micro-grid

由表1可知，孤岛型微网运行有6种状态。当储能故障或输出不足时，储能系统失去平滑作用[18-19]，网内光伏电源和风电机组不能单独持续稳定地给负荷供电，此时仅由柴油机组输出，需要进行负荷消减来维持可靠性高的负荷正常运行。若都发生故障则微网停止运行。

2.2 孤岛微网负荷切除原则

当微网输出不足或储能故障时，需要对负荷进行切除以维持功率平衡。基于负荷划分的思想，综合考虑重要性和位置分析负荷消减原则[20]。

（1）负荷的分块。负荷回路不一定都装低频减载的智能开关，不能任意断开切除。因此，在负荷削减时必须以智能开关为边界分块切除。

（2）为保证内部重要性高的负荷供电，负荷应从重要性低到高的顺序切除削减。另外，相关文献表明，微电源下游的负荷对上游负荷可靠性影响较低，优先切除较远的负荷。

综合式（1）、式（2），定义负荷切除系数为

式中：αi和LZn分别为第i块负荷和第n个负荷点的重要性系数；βi为第i块负荷位置系数，由第n负荷点与微网电源和储能的电气距离dn得到；PLi负荷块的切除系数，综合比较位置和重要性系数获取，对PLi较小的负荷块孤岛运行时优先切除。

3 基于储能运行策略的可靠性评估方法

3.1 储能系统运行策略

储能系统的充放电状态主要取决于光伏电源、风电机组、柴油机组输出和负荷的大小，通常采用以下运行策略[2-8]。

策略1：计算仿真时间内光伏电源和风电机组的平均功率，当分布式电源输出高于平均功率输出时，储能系统充电；低于平均功率输出时，为了使光伏电源、风电机组和储能总出力达到平均水平，储能系统放电。

策略2：分布式发电和柴油机组总功率输出高于负荷需求时，储能系统充电；低于负荷需求时，储能系统放电，分布式电源和储能总出力不得超过全部负荷的x%，常取30%。

策略3：分布式发电和柴油机组总功率输出高于负荷需求时，储能系统充电；低于负荷需求时，储能系统放电。

3.2 可靠性评估方法

孤岛型微网内部电源与储能系统功率输出具有随机、时序等特性，使传统的配电网可靠性评估方法不再适用；另外储能系统的运行状态和运行策略对系统持续稳定供电造成较大的影响。本文结合时序蒙特卡罗法和储能系统3种运行方式，提出如下可靠性评估方法：

（1）初始化数据，系统初始化并确定模拟时间。

（2）计算每个元件的工作时间Tm=-1n δ/λ，δ1，δ2，…，δn为（0，1）间的随机数。由min（Tm）定位故障元件，TTF=min（Tm）为运行时间，并开始计算模拟时间。

（3）元件的故障持续时间TTR=-1n ω/u为修复时间，其中ω为（0，1）间的随机数，u为故障修复率。

（4）根据故障遍历搜索，以智能开关为边界对负荷分类：a类负荷为与微网电源断开连接的负荷，该类负荷在故障修复前一直停运；b类负荷为与微网电源相连的负荷，该类负荷需进行可靠性分析。

（5）令t=1，针对储能系统3种不同运行策略分别分析孤岛型微网的供电可靠性。

策略1的步骤如下：

步骤1分别计算第 t时刻 PPVG（t）、PWTG（t）、PDGS（t）、PPL（t）以及仿真时间内 PVG和 WTG共同输出的平均功率 PA。

步骤 2若PPVG（t）+PWTG（t）=PSUM（t）≥PA，储能系统充电，Pbat（t）=PSUM（t）-PA，储能容量累计为Vbat（t+1）=Vbat（t）+Vin，此时分布式电源与储能共同功率输出PSUM&bat（t）=PA，转至步骤4；否则，下一步。

步骤3此时储能系统放电Pbat（t）≤Pdch-max，若PSUM+Pbat（t）≥PA，则有光伏电源和风电机组与储能共同输出PSUM&bat（t）=PA；否则，PSUM&bat（t）=PSUM+Pbat（t），此时剩余储能容量累计为Vbat（t+1）=Vbat（t）-Vout；转至步骤4。

步骤 4若 PSUM&bat（t）+PDGS（t）≥PL（t），负荷能够持续供电；否则，负荷切除消减。

步骤5更新切除负荷 Ished和剩余负荷 Iremain，累计切除负荷的停电时间及停电次数。

步骤6若t＜Tm+TTF，令 t=t+1，则返回步骤1；否则进行步骤6。

策略 2的步骤如下：

步骤1计算t时刻PPVG（t）、PWTG（t）、PDGS（t）、PL（t）。

步骤 2若PPVG（t）+PWTG（t）=PSUM（t）≥x%PL（t），储能充电，有Pbat（t）=PSUM（t）-x%PL（t），储能容量累计Vbat（t+1）=Vbat（t）+Vin。此时若柴油机组功率PDGS（t）≥（1-x%）PL（t），则系统正常供电；否则，切除负荷，更新Ished、Iremain，累计切除负荷的停电时间及停电次数；转至步骤4。若PSUM＜x%PL（t），则进行下一步。

步骤3若PDGS（t）+PSUM（t）≥PL（t），则系统正常供电。否则，储能放电Pbat（t）=min{Pdch-max，x%PL（t）-PSUM（t）}，剩余容量累计有 Vbat（t+1）=Vbat（t）-Vout；此时若PDGS（t）+PSUM（t）+Pbat（t）≥PL（t），负荷持续供电，否则进行负荷切除消减，更新Ished、Iremain，累计停电时间及停电次数。

步骤4若t＜Tm+TTF，令t=t+1，则返回步骤1；否则，进行步骤6。

策略3的步骤如下：

步骤1计算第t时刻PPVG（t）、PWTG（t）、PDGS（t）、PL（t）。

步骤2若PPVG（t）+PWTG（t）=PSUM（t）≥PL（t），系统正常供电，储能充电，有 Pbat（t）=PSUM（t）-PL（t），储能容量累计Vbat（t+1）=Vbat（t）+Vin；转至步骤5。否则继续下一步。

步骤3此时需要柴油机组输出供电，若PDGS（t）+ PSUM（t）≥PL（t），系统正常运行。否则储能放电输出Pbat（t）≤Pdch-max，储能容量累计Vbat（t+1）=Vbat（t）-Vout。

步骤 4若 PDGS（t）+PSUM（t）+Pbat（t）≥PL（t），则系统正常运行；否则需要切除负荷维持功率平衡，更新Ished、Iremain，累计停电时间及停电次数。

步骤5若t＜Tm+TTF，令t=t+1，则返回步骤1；否则运行步骤6。

步骤6判断运行时间t是否达到模拟时间，若是，运行下一步；否则，返回步骤2。

步骤7根据各负荷点累计的停电时间和总停电次数，计算得到孤岛型微网系统可靠性指标。

算法流程如图2所示。

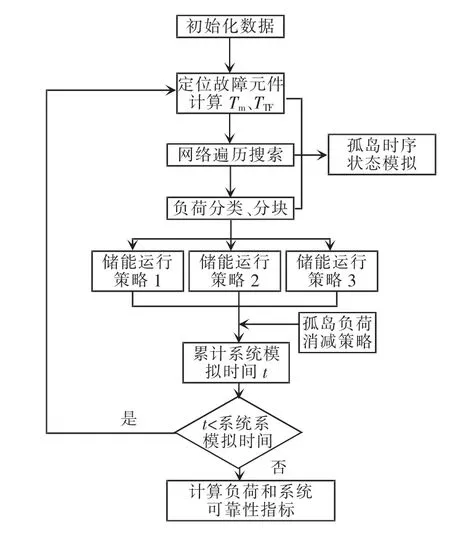
图2 可靠性评估算法流程Fig.2 Flow chart of reliability evaluation algorithm

4 仿真分析

4.1 系统参数

本文采用评估可靠性测试系统RBTS BUS6的改进系统进行仿真分析，选取主馈线F4部分负荷组成孤岛型微网。分布式电源主要由风电机组、光伏电源、柴油发电机和储能组成，如图3所示。

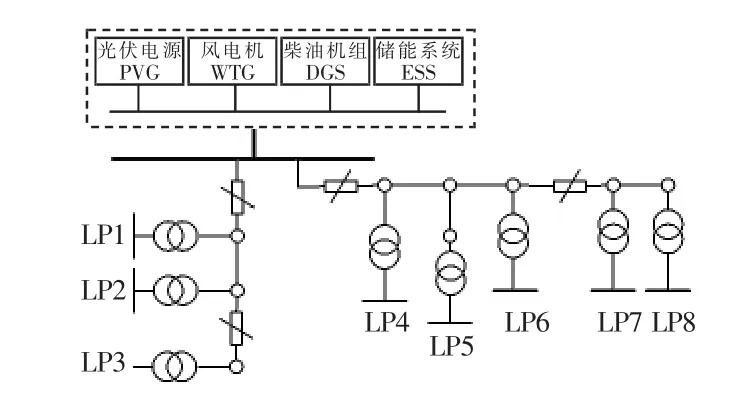
图3 RBTS Bus6改进系统Fig.3 Improved RBTS Bus6 system

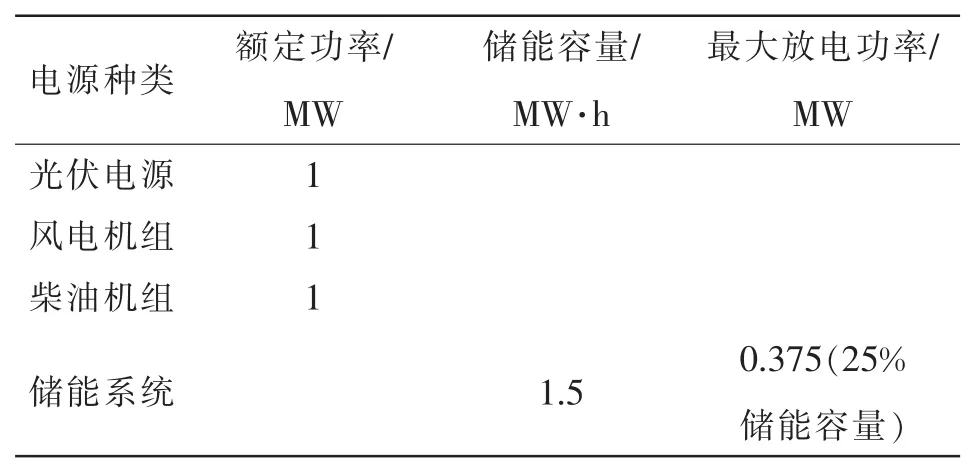
表2 分布式电源和储能参数Tab.2 Parameters of distributed power and energy storage

表3 元件可靠性参数Tab.3 Component reliability parameters

光伏电源中 α=3.034、β=2.299最大光强xmax= 1.029 kW/m2、风电机组中 Vci=10.8 km/h、Vr=28.8 km/h、Vco=54 km/h，风能渗透率x%为30%，其他参数[6]见表2和表3。

4.2 可靠性评估结果

运用本文所提方法对该测试微网系统进行可靠性评估，3种不同运行策略下的负荷点的可靠性评估指标如图4和图5所示。

图4 不同策略下负荷点停电次数Fig.4 Power outages of load points with different strategies

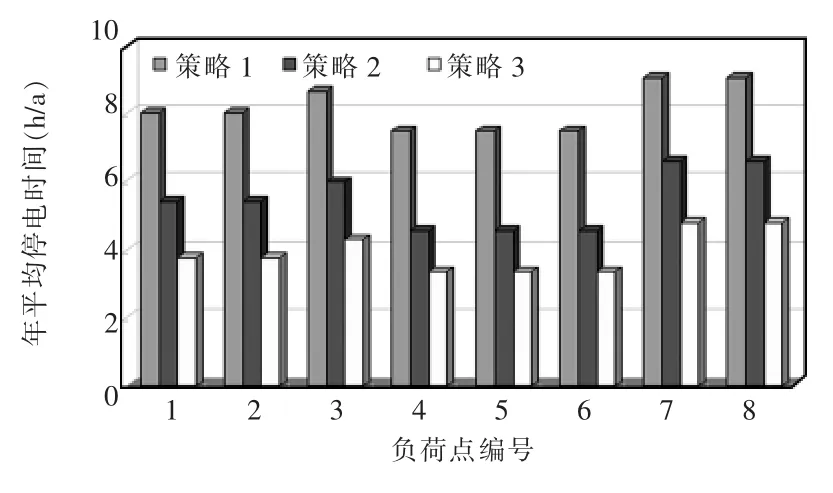
图5 不同策略下负荷点平均停电时间Fig.5 Average outage time of load points with different strategies

表4 孤岛型微网系统的可靠评估指标Tab.4 Reliability indices of isolated island micro-grid system

根据图4和图5负荷点指标可以分析孤岛型微网系统的评估指标[21]：系统平均停电频率SAIFI、系统平均停电持续时间SAIDI、平均供电可用率AISI（average service availability index）、系统供电量指标EENS，结果如表4所示。

由以上仿真结果可知：

（1）针对孤岛型微网时序、随机等运行特性，采用上述所提算法能有效评估孤岛型微网的供电可靠性。

（2）负荷切除原则对孤岛型微网内部重要负荷持续供电有重要意义。由图4、图5可知负荷点4、5、6所在的负荷块的切除系数较大，即进行消减时最后切除，可靠性高。但负荷点7、8所在负荷块切除系数较小，优先切除，可靠性低。

（3）储能运行特性和运行策略对孤岛型微网的可靠性有较大影响。策略1的储能供电量和充放电次数均高于策略2和策略3，当分布式电源输出不足时容易造成停电事故；策略2和策略3均在分布式电源输出过剩时给储能充电，策略3提高了新能源利用率，减少了负荷消减，提高了供电可靠性。

5 结语

本文研究了光强和风速模型及光伏电源和风电机组功率输出的随机特性，针对孤岛型微网的运行特性，提出了3种不同的储能运行策略，并建立了孤岛型微网运行全时序可靠性评估模型。在此基础上，基于负荷消减策略提出了适用于计算孤岛型微网可靠性评估指标的方法，并在实际算例中进行了仿真运算。运算结果表明：储能系统的运行策略对负荷点及微网系统的可靠性有很大的影响。所提方法的有效性和合理性在仿真中得到验证，结果更合理、符合实际。

[1]解翔,袁越,邹文仲,等.非计划孤岛下的微电网供电可靠性评估[J].电力系统自动化,2012,36（9）：18-22.

Xie Xiang,Yuan Yue,Zou Wenzhong,et al.Reliability evaluation of microgrid power supply in emergency nonscheduled isolated mode[J].Automation of Electric Power Systems,2012,36（9）：18-22（in Chinese）.

[2]谢开贵,王岸,胡博.计及储能设备运行策略的风/柴/储混合系统可靠性评估[J].电力系统保护与控制,2012,40（9）：1-7.

Xie Kaigui,Wang An,Hu Bo.Reliability evalu ation of wind-diesel-storage hybrid system considering operating strategies of energy storage system[J].Power System Protection and Control,2012,40（9）：1-7（in Chinese）.

[3]Bae I S,Kim J O,Reliability evaluation ofdistributed generation based on operation mode[J].IEEE Trans on Power Systems,2007,22（2）：785-790.

[4]Bollen M H J,Sun Y,Ault G W.Reliability of distribution networks with DER including intentional islanding[C]. 2005 International Conference on Future Power Systems. Amsterdam,Netherlands：IEEE,2005.

[5]王玉梅,吴志明.基于时序模拟的并网型微网可靠性分析[J].电源学报,2015,13（4）：101-108.

Wang Yumei,Wu Zhiming.Reliability analysis of gridconnected microgrid using sequential simulation[J].Journal of Power Supply,2015,13（4）：101-108.（in Chinese）.

[6]梁惠施,程林,刘思革.基于蒙特卡罗模拟的含微电网配电网可靠性评估[J].电网技术,2011,35（10）：76-81.

Liang Huishi,Cheng Lin,Liu Sige.Monte carlo simulation based reliability evaluation of distribution system containing microgrids[J].Power System Technology,2011,35（10）：76-81（in Chinese）.

[7]王杨,万凌云,胡博,等.基于孤岛运行特性的微电网可靠性分析[J].电网技术,2014,38（9）：2379-2385.

Wang Yang,Wan Lingyun,Hu Bo,et al.Isolated island operating characteristics based analysis on reliability of microgrid[J].Power System Technology,2014,38（9）：2379-2385（in Chinese）.

[8]王杨,谢开贵,胡博,等.基于时序模拟的离网型微电网可靠性分析[J].中国电工技术学会学术年会,2014.

Wang Yang,Xie Kaigui,Hu Bo,et al.Reliability analysis of islanded microgrid based on sequential simulation[J]. Academic Annual Meeting of China Electrotechnical Society.2014

[9]兰华,李政阳,王韵然.风光互补发电系统对配电网可靠性的影响[J].电源学报,2012,10（6）：92-96.

Lan Hua,Li Zhengyang,Wang Yunran.Research on the influence of wind-solar hybrid power supply system to the reliability of distribution network[J].Journal of Power Supply,2012,10（6）：92-96.（in Chinese）.

[10]Abouzahr I,Ramakumar R.An approach to assess the performance of utility-interactive photovoltaic systems[J]. IEEE Transactions on Energy Conversion,1993,8（2）：145-153.

[11]Karaki S H,Chedid R B,Ramadan R.Probabilistic performance assessment of autonomous solar-wind energy conversion systems[J].IEEE Transactions on Energy Conversion,1999,14（3）：766-772.

[12]Abouzahr I,Ramakumar R.Loss of power supply probability of stand-alonephotovoltaic systems：a closed form solution approach[J].IEEE Transations on Energy Conversion,1991, 6（1）：1-11.

[13]王成山,郑海峰,谢莹华,等.计及分布式发电的配电系统随机潮流计算[J].电力系统自动化,2005,29（24）：39-44.

WANG Chengshan,ZHENG Haifeng,XIE Yinghua,et al. Probabilistic power flow containing distributed generation in distribution system[J].Automation of Electric Power Systems, 2005,29（24）：39-44（in Chinese）.

[14]丁明,吴义纯,张立军.风电场风速概率分布参数计算方法的研究[J].中国电机工程学报,2005,25（10）：107-110.

Ding Ming,Wu Yichun,Zhang Lijun.Study on the algorithm to the probabilistic distribution parameters of wind speed in wind farms[J].Proceedings of the CSEE,2005,25（10）：107-110（in Chinese）.

[15]张文亮,丘明,来小康.储能技术在电力系统中的应用[J].电网技术,2009,32（7）：1-9.

Zhang Wenliang,Qiu Ming,Lai Xiaokang.Application of energy storage technologies in power grids[J].Power System Technology,2009,32（7）：1-9（in Chinese）.

[16]徐玉琴,吴颖超.考虑风力发电影响的配电网可靠性评估[J].电网技术,2011,35（4）：154-158.

Xu Yuqin,Wu Yingchao.Reliability evalution for distribution system connected with wind-turbine generators[J]. Power System Technology,2011,35（4）：154-158（in Chinese）.

[17]Suchismita S,Chanan S.A reliability assessment methodology for distribution systems with distributed generation[C] //Power Engineering Society General Meeting.Montreal, Canada：IEEE,2006：1-7.

[18]陈益哲,张步涵,王江虹,等.基于短期负荷预测的微网储能系统主动控制策略[J].电网技术,2011,35（8）：35-40.

Chen Yizhe,Zhang Buhan,Wang Jianghong,et al.Active control strategy for microgrid energy storage system based on short-term load forecasting[J].Power System Technology,2011,35（8）：35-40（in Chinese）.

[19]Bahramirad S,Reder W,Khodaei A.Reliability constrained optimal sizing of energy storage system in a microgrid[J].IEEE Transactions on Smart Grid,2012,3（4）：2056-2062.

[20]刘洋,周家启.大电网可靠性评估最优负荷削`减模型[J].重庆大学学报,2003,26（10）：52-55.

Liu Yang,Zhou Jiaqi.Optimal load curtailment in bulk power system reliability evaluation[J].Journal of Chongqning University,2003,26（10）：52-55（in Chinese）.

[21]罗奕,王钢,汪隆君,微网可靠性评估指标研究[J].电力系统自动化,2013,37（5）：9-13.

Luo Yi,Wang Gang,WANG Longjun.Reliability evaluation indices for microgrid[J].Automation of Electric Power Systems,2013,37（5）：9-13.