基于符号动力学的DC/DC开关变换器“周期3即混沌”证明

王燕芬，杨 汝，元达鹏

（广州大学物理与电子工程学院，广州 510006）

近30年来，非线性动力学与混沌在电路与系统理论方面已经被广泛关注，数学与系统理论在研究混沌发生及其产生的根源方面取得显著的成果[1-5]。传统DC/DC开关变换器的非线性动力学研究主要集中在分岔和混沌，分岔通向混沌的过程一方面通过用Poincare截面画出系统参数的分岔图[6]，观察周期分岔级联的精细结构；另一方面则从数学上提出稳定性的判据和分岔产生的条件[7]。

符号动力学是在有限精度下对动力学过程实行严格描述的一套方法。应用符号动力学方法，可以把动力系统极复杂的行为用简单的符号序列方法表示出来。符号动力学及其在研究非线性系统周期和混沌运动中的应用，已经取得了很好的结果。符号动力学提供一种严谨的方法，有助于理解周期和混沌的全局特性[8]、周期解的普适性[9]、混沌吸引子的结构[10]、微分方程的分岔特性[11]等。

本文基于广义合成律，用符号动力学的基本内容分析DC/DC开关变换器。周期3是混沌带中最为明显的一个周期窗口，也是很特殊的周期轨道。由切分岔定理[12]可知，开关变换系统发生切分岔是导致周期3和阵发混沌产生的根源，分析周期3窗口对研究非线性现象有重要的意义。华人学者李天岩和美国数学家Yorke[13]从数学的角度证明“周期3意味着混沌”，但其证明过程很抽象。本文用广义合成律首次证明Boost变换系统中存在周期3，则存在任意周期n轨道，证明过程简单易懂，最后用仿真实验证明研究方法的可靠性。广义合成律对“周期3意味着混沌”的深入证明，为探索和揭示非线性开关变换器系统的动力学复杂行为提供了新的研究理论。

1 Boost变换器的动力系统模型

1.1 1阶动力系统

电压反馈控制的Boost变换器如图1所示。电路参数为：输入电压E=16 V，输出电压X=25 V，开关周期T=333.33 μs，电感L=208 μH，负载电阻R= 12.5 Ω，电容C=222 μF，稳态占空比Ds=0.287 4，反馈比例增益k=0.07～0.16。若电路工作于不连续电流模式 DCM（discontinuous current mode），在开关周期到来前，开关管S和二极管D都不导通，电感电流iL降到0，即iL（nT）=0，T为开关周期。以输出电容电压 vc为状态变量 x，则有 xn=vc（tn）=vc（nT），可得到DCM Boost变换器1阶离散时间映射[14]近似为

当k=0.08时，式（1）的映射如图2所示。由图可见，DCM Boost变换器的1阶离散时间映射是个倒单峰映射，称之为单谷映射。因此，可以直接运用倒单峰映射系统的排序和演化规律的符号动力学来分析1阶Boost开关动力系统的动力学性质。

图1 电压模式控制的Boost变换器Fig.1 Voltage-mode controlled Boost converter

图2 1阶迭代映射（xn+1-xn）Fig.2 First-order iterative map（xn-xn+1）

倒单峰映射周期轨道（LR…C）的特点字母是最大值R的前一点对应最小值L，而最小值L的前一点对应C或其近邻的R或L，参照C的数值大小来确定其他轨道点xn所对应的字母，确定其周期轨道窗口。用此方法可确定一系列周期窗口的符号序列。以反馈比例增益k为分岔参数，则1阶Boost开关动力系统的符号序列和窗口参数如表1和图3所示。

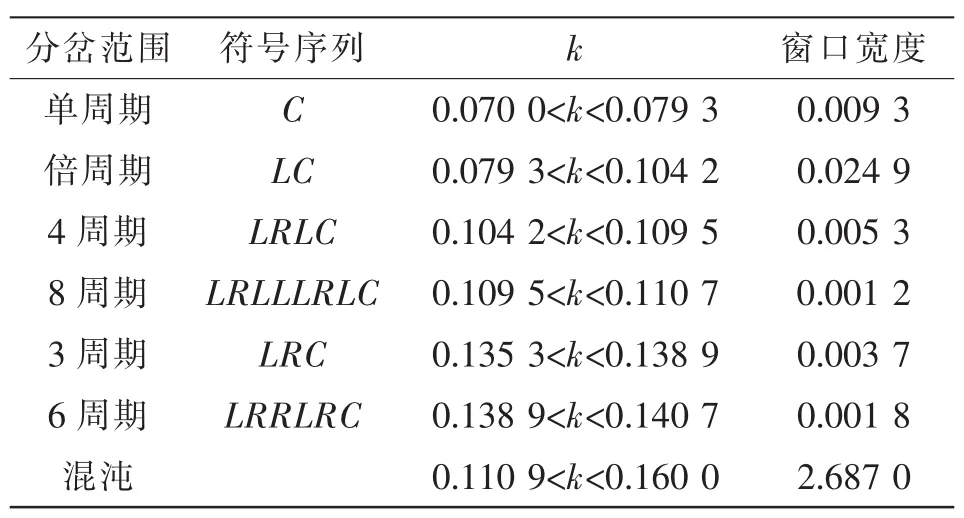
表1 以k为分岔参数的周期窗口Tab.1 Periodic windows with k as bifurcation parameter

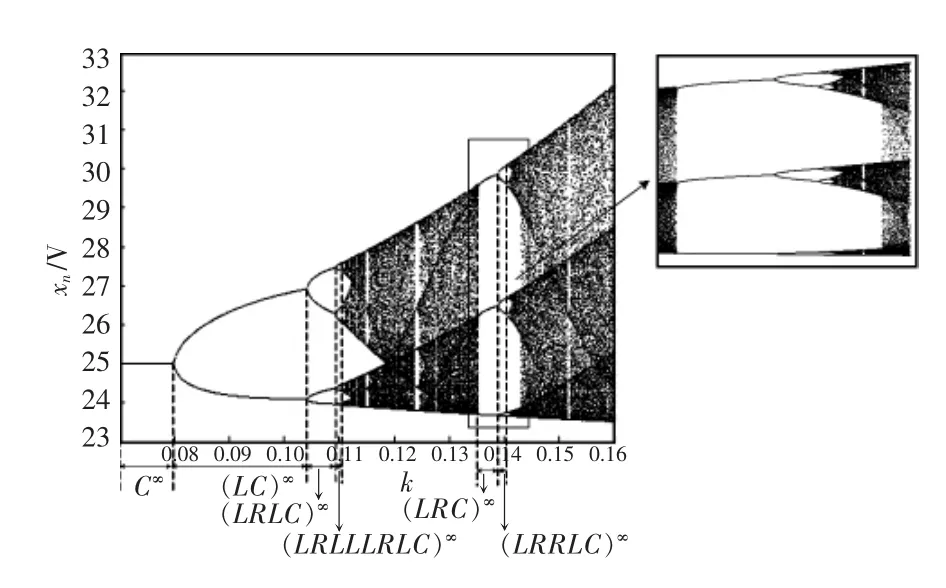
图3 1阶Boost开关动力系统分岔参数及部分符号序列Fig.3 Bifurcation and partial symbolic sequences of the first-order Boost switching dynamical system

1.2 2阶动力系统

峰值电流模式控制的Boost变换器的2阶离散系统如图4所示，开关管S状态改变，变换器的电路拓扑也发生变化。选取合适的电路参数，L=1 mH，C=12 μF，R=15 Ω，Vin=10 V，fs=10 kHz，Iref=1～6.0 A，变换器工作于连续电流模式CCM（continuous current mode），系统在两种电路拓扑结构之间切换，对应的状态方程分别为

式中：vc为电容输出电压；iL为电感电流。

当Iref=4.3 A时，对变换器系统按驱动周期进行采样，得到变换器系统Poincare截面（iL（n），vc（n））,再取（iL（n），iL（n+1））或（vc（n），vc（n+1））构成电流或电压首归映射，如图5所示。

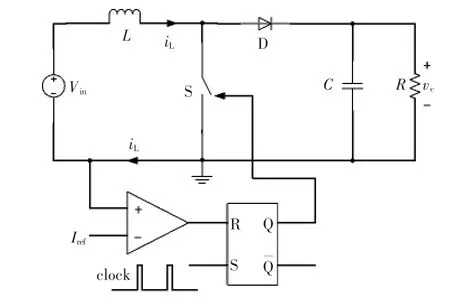
图4 峰值电流模式控制的Boost变换器原理Fig.4 Schematic of peak current-mode controlled Boost converter

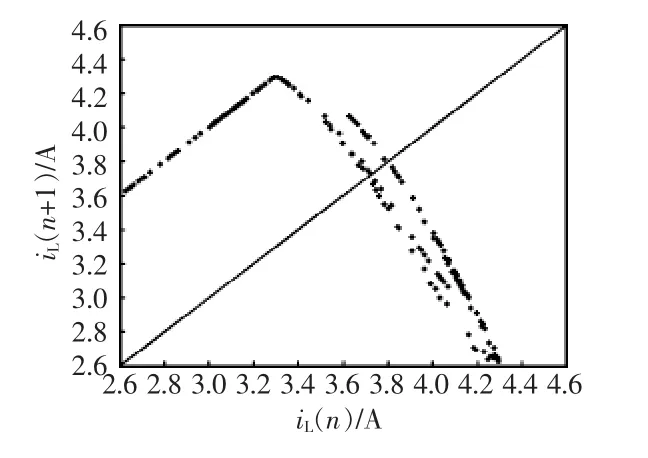
图5 电流的首归映射iL（n）→iL（n+1）Fig.5 Return map current iL（n）→iL（n+1）

图5显示出折叠和非一维的结构，但是因为符号动力学的分析方法本来就是粗粒化，故只要放粗观察精度，仍然相当于接近一维[16]，而且是1个单峰映射。因此，可以直接运用单峰映射系统的排序和演化规律的符号动力学来分析2阶Boost开关动力系统的一些动力学性质。

单峰映射周期轨道（RL…C）的特点字母是最小值L的前一点对应最大值R，而最大值R的前一点对应C或其近邻的R或L，参照C的数值大小来确定其他轨道点in所对应的字母，这样就确定周期轨道窗口。用这种方法可以确定一系列周期窗口的符号序列，2阶Boost开关动力系统的符号序列和窗口参数范围见表2和图6。

1.3 周期3的诞生

1阶和2阶Boost开关动力系统的分岔参数在混沌区域内出现一个较大的周期3窗口，其局部分岔如图3和图6所示，周期窗口中周期3轨道遍历相似的倍周期分岔后通向混沌通道，并在周期窗口结束，发生混沌危机，引发混沌状态的突变。混沌危机的出现是由于不稳定周期轨道与次级混沌带相遇，引发混沌带中的轨道充斥于整个混沌区域[15]。

表2 以Iref为分岔参数的周期窗口Tab.2 Periodic windows with Irefas bifurcation parameter

图6 2阶Boost开关动力系统的分岔参数及部分符号序列Fig.6 Bifurcation parameter and partial symbolic sequences of the second-order Boost switching dynamical system

由图2可见，当参数k增大到1.352 6附近时，1阶Boost开关动力系统产生切分岔，引发阵发混沌，出现周期3。图7给出在k=1.352 6附近的3次迭代曲线，与对角线相切，产生了3个切口A、B、C和一个不稳定的交点D。3个切点形成了稳定的周期轨道和3条不稳定轨道，3条不能观察到的不稳定轨道在窗口结束处与次级混沌带相遇，从而引发混沌危机。同理，对于2阶Boost开关动力系统系统，当参数Iref增大到5.804附近时，Boost变换器产生切分岔，引发阵发混沌。

图7 1阶Boost开关动力系统的3次迭代曲线Fig.7 Cubic iterative curve of the first-order Boost switching dynamical system

2 广义合成律分析周期3

2.1 广义合成律的变换规则

符号动力学指出，满足同一拓扑映射的动力学系统，其对应的揉序列排序具有普适性[17]。通常，把一个动力学系统、满足允字条件的符号序列由小到大排列，称为“MSS序列”[18]。截至周期6的单峰映射和倒单峰映射的MSS表分别如表3和表4所示。

表3 周期6以内的倒单峰映射MSSTab.3 Inverted unimodal map MSS up to period 6

表4 周期6以内的单峰映射MSSTab.4 Unimodal map MSS up to period 6

广义合成律是运用符号序列对不同周期轨道间进行有据变换的一种粗粒化的数学工具，具体的证明见文献[16]。广义合成律的变换规则如下：

除了L∞外的任意符号序列字，做满足以下3条件的变换后所得的符号序列仍为符号序列字。

（1）ρ为奇，而λ为偶，其中ρ和λ为R和L组成的有限长度符号序列；

（2）ρ＞λ；

（3）ρ|C、ρλ|C和ρλ∞均为揉序列字。

2.2 1阶Boost变换器周期3符号动力学分析

如果存在周期3，无论系统稳定或非稳定，则必存在任意周期n的轨道。这就是“周期3意味着混沌”这一说法的意义。

对于Boost变换器的一阶动力系统，稳定周期3由序列（LRL）∞开始，如果写成

则取ρ=L和λ=RLL时，ρ和λ满足广义合成律的3条件。还可以写成

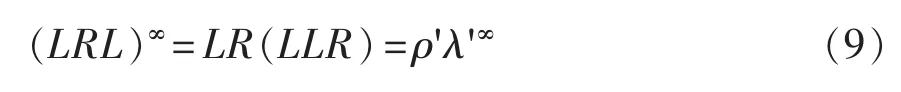
这时ρ'=LR和λ'=LLR也满足上述3条件。

因为符号序列（LRn）∞跟（LRm+1LL）∞都是表 1里面的序列，故根据式（9）和式（10），可由R和L的允许序列生成新的允许序列，即

则式（10）的周期分别3n+1，3n+2和3n，于是，可以得到周期任意长的符号序列。由此验证“周期3意味着混沌”这一说法的意义。

周期3发生之前，存在短暂的阵发混沌，借助符号动力学，也可较深刻地理解阵发混沌。在小于（LRL）∞一侧，可找到随参数k增大，周期间歇长度递增的符号序列系列[ρ（LRL）m]∞，m=1，2，…，当m→∞时，变成ρ（LRL）∞，是一个周期3轨道。

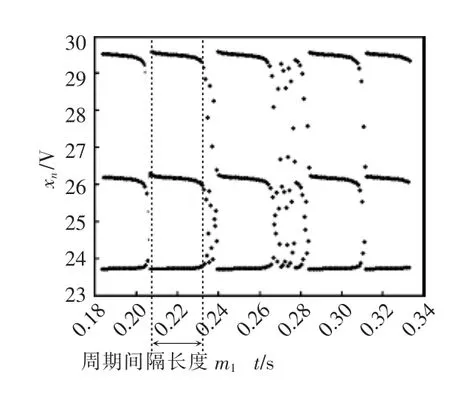
图8 k=0.135 20时1阶Boost开关动力系统阵发混沌Fig.8 Intermittent chaos of the first-order Boost switching dynamical system with k=0.135 20

图9 k=0.135 23时1阶Boost开关动力系统阵发混沌Fig.9 Intermittent chaos of the first-order Boost switching dynamical system with k=0.135 23

此[ρ（LRL）m]∞型的粗粒混沌系列表现出阵发混沌，并且幂次m刻画周期间歇的长度，如图8和图9所示，参数k越大，周期间隔越长，最后形成稳定周期3轨道。

2.3 2阶Boost的变换器周期3符号动力学分析

同理，对于Boost变换器的2阶动力系统，稳定周期3由序列（RLR）∞开始，如果写成

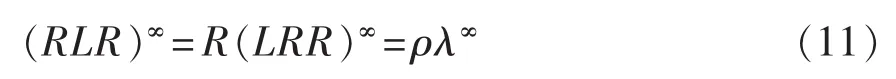
则取ρ=R和λ=LRR时，ρ和λ满足广义合成律的3条件。还可以写成

这时ρ'和λ'也满足上述3条件。

图10 Iref=5.530 30时2阶Boost开关动力系统阵发混沌Fig.10 Intermittent chaos of the second-order Boost switching dynamical system with Iref=5.530 30

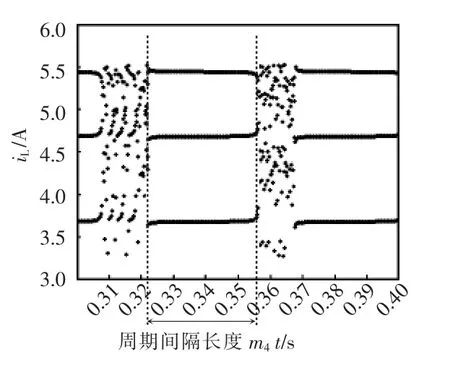
图11 Iref=5.530 56时2阶Boost开关动力系统阵发混沌Fig.11 Intermittent chaos of the second-order Boost switching dynamical system with Iref=5.530 56

根据式（12）和式（13），可由R和L的允许序列生成新的允许序列，即则式（13）的周期分别3n+1，3n+2和3（n+1），于是，可以得到周期任意长的符号序列。

在小于（RLR）∞一侧，可找到随m增大周期间歇长度递增的符号序列系列[ρ（LRR）m]∞，m=1，2，…。当m→∞时，变成ρ（LRR）∞，这也是一个周期3轨道，[ρ（LRR）m]∞型的粗粒混沌系列表现出阵发混沌，并且幂次m刻画周期间歇的长度，如图8和图9所示，参数k越大，周期间隔越长，最后形成稳定周期3轨道。

3 仿真实验

基于式（7）和式（8）的分段线性模型，按照上述2阶变换系统的电路参数，对峰值电流模式控制Boost变换器进行了电路实验，得到稳定周期3以及发生切分岔前的阵发混沌的电感电流iL和电容电压uc的时域波形和Poincare截面，如图12所示。其中图（b）和（d）是151个采样点的Poincare截面。

图12 Boost变换器的电感电流和电容电压特性Fig.12 Inductor current and capacitor voltage characteristics of Boost converter

4 结语

本文分别以1阶和2阶Boost开关动力系统为例，首先证明周期3发生的根源是系统发生切分岔；其次从符号动力学的角度用广义合成律具体举例证明“周期3意味着混沌”这一说法的符号含义；接着用符号序列的幂次代表阵发混沌发生的周期间隔，并分别附图证明随着参数k和Iref增大，1阶和2阶的变换系统阵发混沌发生的周期间隔也越长；最后形成稳定周期3轨道。分析混沌带中的周期3以及“周期3意味着混沌”的深入证明，对了解Boost变换器非线性全局稳定性具有重要意义。

[1]Jackson L,Lindgren A,Kim Y.A chaotic attractor from Chua’s circuit[J].IEEE Transactions on Circuits and Systems,1984,31（12）：1055-1058.

[2]Murali K,Lakshmanan M.Effect of sinusoidal excitation on the Chua's circuit[J].IEEE Transactions on Circuits and Systems I：Fundame-ntal Theory and Applications,1992,39（4）：264-270.

[3]Maggio G M,De Feo O,Kennedy M P.Nonlinear analysis of the Colpitts oscillator with applications to design[J]. IEEE Transactions on Circuits and Systems I：Fundamental Theory and Applications,1999,46（9）：1180-1130.

[4]张波,曲颖.ZCS BUCK变换器CM工作模式下的分岔和混沌现象[J].电源学报,2004,2（4）：251-255.

Zhang Bo,Qu Ying.The bifurcation and chaotic phenomena in ZCS buck converter operating under CM Mode[J].Journal of Power Supply,2004,2（4）：251-255（in Chinese）.

[5]张波.DC-DC变换器非线性混沌现象研究[J].电源学报, 2003,1（4）：491-496.

Zhang Bo.Study on nonlinear chaotic phenomenon of DCDC converters[J].Journal of Power Supply,2003,1（4）：491-496（in Chinese）.

[6]王学梅,张波,丘东元.不连续导电模式DC-DC变换器的倍周期分岔机理研究[J].物理学报,2008,57（5）：2728-2736.

Wang Xuemei,Zhang Bo,Qiu Dongyuan.Mechanism of period-doubling bifurcation in DCM DC-DC converter[J]. Acta Physica Sinica,2008,57（5）：2728-2736（in Chinese）.

[7]杨汝,张波,褚利丽.开关变换器倍周期分岔精细层次结构及其普适常数研究[J].物理学报,2008,57（5）：2770-2778.

Yang Ru,Zhang Bo,Chu Lili.Research of fine stracture and universal constants of bifurcation in converters[J]. Acta Physica Sinica,2008,57 （5）：2770-2778（in Chinese）.

[8] HaoBailin,Liu Junxian,ZhengWeimou.Symbolic dynamics analysis of the Lorenz equations[J].Physical Review E,1998,57（5）：5378.

[9]王光瑞,张淑誉,郝柏林.强迫布鲁塞尔振子周期解的普适序列[J].物理学报,1984,33（7）：1008-1016.

Wang Guangrui,Zhang Shuyu,Hao Bailin.U-Sequence of periodic solutions in the forced Brus selator[J].Acta Physica Sinica,1984,33（7）：1008-1016（in Chinese）.

[10]Zheng Weimou,Liu Junxian.Symbolic analysis of attractor geometry for the Lozi map[J].Physical Review E,1994,50（4）：3241.

[11]Xie Fagen,Zheng Weimou,Hao Bailin.Symbolic dynamics of the two-well duffing equation [J]. Communications in Theoretical Physics,1995,24（1）：43.

[12]郝柏林.从抛物线谈起——混沌动力学引论[M].2版.北京：北京大学出版社,2013.

[13]Li T Y,Yorke J A.Period three implies chaos[J].The American Mathematical Monthly,1975,82（10）：985-992.

[14]Tse C K.Flip bifurcation and chaos in three-state boost switching regulators[J].IEEE Transactions on Circuits and Systems I：Fundamental Theory and Applications,1994, 41（1）：16-23.

[15]包伯成.混沌电路导论[M].北京：科学出版社,2013.

[16]郑伟谋,郝柏林.实用符号动力学[M].上海：上海科技教育出版杜,1995.

[17]郝柏林.实用符号动力学与混沌[M].2版（英文版）.北京：北京大学出版社,2014.

[18]Metropolis N,Stein M L,Stein P R.On finite limit sets for transformations on the unit interval[J].Journal of Combinatorial Theory,Series A,1973,15（1）：25-44.